COMPARISON OF DIFFERENT CLASSIFIERS ON A REDUCED

SET OF FEATURES FOR MENTAL TASKS-BASED BRAIN

COMPUTER INTERFACE

Giovanni Saggio, Pietro Cavallo, Giovanni Costantini, Gianluca Susi

Dept. of Electronic Engineering, “Tor Vergata” University, Via del Politecnico 1, 00133 Rome, Italy

Lucia Rita Quitadamo

, Maria Grazia Marciani, Luigi Bianchi

Dept. of Neuroscience, “Tor Vergata” University, Via Montpellier 1, 00133 Rome, Italy

Fondazione Santa Lucia, IRCCS, Neuroelectrical Imaging and BCI Laboratory, Via Ardeatina 306, 00179, Rome, Italy

Centro di Biomedicina Spaziale, “Tor Vergata” University, Rome, Italy

Keywords: BCI, Neural Networks, Fuzzy Logic, SVM.

Abstract: In this study a comparison among three different machine learning techniques for the classification of

mental tasks for a Brain-Computer Interface system is presented: MLP neural network, Fuzzy C-Means

Analysis and Support Vector Machine (SVM). In BCI literature, finding the best classifier is a very hard

problem to solve, and it is still an open question. We considered only ten electrodes for our analysis, in

order to lower the computational workload. Different parameters were analyzed for the evaluation of the

performances of the classifiers: accuracy, training time and size of the training dataset. Results

demonstrated how the accuracies of the three classifiers are nearly the same but the error margin of SVM on

this reduced dataset is larger compared to the other two classifiers. Furthermore neural network needs a

reduced number of trials for training purposes, reducing the recording session up to 8 times with respect to

SVM and Fuzzy analysis. This suggests how, in the presented case, MLP neural network can be preferable

for the classification of mental tasks in Brain Computer Interface systems.

1 INTRODUCTION

A Brain Computer Interface (BCI) system allows a

subject to act on his environment by means of his

thoughts, without using the brain normal output

pathways of muscles or peripheral nerves (Wolpaw,

2002).

This system intends to furnish people with motor

disabilities an alternative communication channel,

by translating some of their brain signals into

commands for piloting an external device such as a

wheelchair, a robotic arm, a Web surfer, a cursor on

a screen, a speech synthesizer, etc. This result can be

obtained by means of the brain signals which are

acquired and then processed to extract some features

of interest from them; these features are then

classified and encoded into semantic symbols that

are finally mapped into the output commands.

Some BCI systems can be driven by mental tasks

(Schögl, 2005), (Huan and Palaniappan, 2004), in

the sense that the user of the system mentally

imagines to perform some particular tasks that are

then recognized by a classifier and used to pilot the

output peripheral. As in the case of the experimental

protocol described in this paper, the subject is asked

to imagine right and left hand movements, to

perform mental calculation and to mentally recite a

nursery rhyme. Feature extraction and classification

of the recorded brain signals finally allow the

mapping of the four mental tasks into commands

toward the final device.

Within the tools for classifications, we

implemented MLP neural network, Fuzzy C-Means

(FCM) analysis and Support Vector Machine

(SVM). MLP and SVM were adopted since they are

well known methods in machine learning literature

while Fuzzy analysis was chosen because, despite it

is a fairly new methodology in this field (Saggio,

2009), it usually performs a highly accurate spatial

separation.We were interested then in comparing the

174

Saggio G., Cavallo P., Costantini G., Susi G., Rita Quitadamo L., Grazia Marciani M. and Bianchi L. (2010).

COMPARISON OF DIFFERENT CLASSIFIERS ON A REDUCED SET OF FEATURES FOR MENTAL TASKS-BASED BRAIN COMPUTER

INTERFACE.

In Proceedings of the Third International Conference on Bio-inspired Systems and Signal Processing, pages 174-179

DOI: 10.5220/0002696301740179

 SciTePress

performances of the three classifiers and, even if in

literature SVM performs a better classification of

EEG signals (Costantini, 2009), we tried to figure

out if this remains true if only a reduced set of

features is considered.

2 METHODS

2.1 EEG Recording and Preprocessing

Dataset was recorded from six subjects, four male

and two female (average age of 23), free of known

neurological disorders. An elastic electrode cap was

used to record EEG signals, supplied with 61 Ag-

AgCl electrodes located according to the

International 10-20 system. The data were recorded

at a sampling rate of 256 Hz and bandpass-filtered

between 0.5 Hz and 128 Hz. The experimental

protocol consisted of four different imagery tasks:

(1) Left hand movement imagination (L)

(2) Right hand movement imagination (R)

(3) Mental subtraction operation (S)

(4) Mental recitation of a nursery rhyme. (N)

Two sessions on distinct days were recorded for

each subject. Each session consisted of 200 trials (50

for each task).

The subjects sat in a dark room in front of a

computer screen. At the beginning of each trial, a

text indicating the task to perform appeared on the

black screen for 3 secs. The inter-trial interval (ITI)

was set to 1 sec.

To reduce the computational workload, only 10

among the 61 electrodes (Fig. 1) were considered,

Figure 1: Placement of the 10 EEG considered electrodes.

being the most relevant for the 4 tasks. We selected

frequencies in the range from 8Hz to 13Hz

(corresponding to α band (Kandel, 2000)) for each

electrode.

This means a drastic reduction in the size of the

training set. For a single trial, the relative powers of

the signals in the above-said band, for each

electrode, were computed, and constituted the

features vector fed to the different classifiers.

2.2 Classifiers

In this section the three classifiers are briefly

introduced. For detailed information and for a better

understanding, one can refer to (Cammarata, 1997;

Mikailov, 1997; Bezdek, 1981; Burges, 1998;

Joachims, 1999) or other texts on machine learning

or pattern recognition. In addition to some details

related to classifiers, explanations about the way

they were used are given.

2.2.1 Artificial Neural Networks

An Artificial Neural Network (ANN) is a

computational model inspired by the way biological

nervous systems, such as the brain, process

information. An ANN is composed of a large

number of interconnected processing elements

(artificial neurons) working to solve specific

problems. It can be configured for a specific

application, such as pattern recognition or data

classification, through a learning process. As well as

biological systems, learning process involves

adjustments to the connections that exist between the

artificial neurones.

We adopted here a type of ANN known as Multi-

Layer Perceptron (MLP) Neural Network made of

four layers: one input, two hidden and one output.

This network is very popular in literature because it

can perform non-linear spatial separation. In MLP

each neuron is connected with a certain weight to

every other neuron in the previous layer. Regularly,

at each time step, the input is propagated through

layers. The input layer has 10 neurons, one for each

considered electrode. For each trial input neurons

receive the relative powers of electrodes normalized

to an average of 0.5 value to make measures

comparable between each other. Now the

information is fed to the first hidden layer through

weighted connections. Each hidden layer is formed

by 20 neurons. Excepted for the input layer, all the

neurons are characterized by a sigmoid activation

function:

COMPARISON OF DIFFERENT CLASSIFIERS ON A REDUCED SET OF FEATURES FOR MENTAL

TASKS-BASED BRAIN COMPUTER INTERFACE

175

)5.0(6

)(

−−

xfs

scaled in the range from 0 to 1. Sigmoid was

preferred due to its independent and fundamental

space division properties (Cammarata, 1997; Hara

and Nakayamma, 1994) as it models the frequency

of action potentials of biological neurons in the

brain. The output layer has 4 neurons, one for each

mental task to be recognized. In case of a successful

classification the output of the neuron corresponding

to the classified task tends to 1 whereas other

outputs tend to 0. Every neuron, except for the input

layer, was initialized with a random weight in the

range of 1

√



⁄

, where n is the number of neurons

connected by means of that weight (Hernandez-

Espinosa and Fernandez Redondo, 2001; Lari-

Najafi, 1989). As commonly done, a constant weight

of 1 was assigned to the input layer.

After the output presentation, a learning rule was

applied. We used a supervised learning method

(Allred and Kelly, 1990) called backpropagation

(Hecht-Nielsen, 1989), which calculates the mean-

squared error between actual and expected output.

The error value is then propagated backwards

through the network, and small changes are made to

the weights in each layer. The weight changes are

calculated in order to reduce the error signal. The

whole process was then repeated for each trial and

the cycle was reiterated until the overall error value

drops below some pre-determined threshold. We

empirically found that the best learning rate

(measuring the greediness of the algorithm) for our

case has to be set around 0.65.

2.2.2 Fuzzy Logic

Fuzzy logic arises as a method to formalize real-

world concepts that cannot be categorically

identified as true or false, but that may have some

degree of truth. The fuzzy logic has particularly

effectiveness in applications of information

extraction and interpretation.

One of the hallmarks of fuzzy logic is that it

allows nonlinear input/output relationships to be

expressed by a set of qualitative “if-then” rules.

Fuzzy rules provide a powerful framework for

capturing and explaining the input/output data

behavior.

Extracting fuzzy rules for pattern classification

can be viewed as the problem of partitioning the

input space into appropriate fuzzy clusters: groups of

trials with similar structural characteristics

(Mikhailov, 1997). This is made by applying the

algorithm Fuzzy C-Means on each n-dimensional

vector of trials containing the relative powers of

each electrode considered. The FCM is a clustering

algorithm based on optimizing an objective function

(Abonyi, 2002). Given a set of elements

xxX ℜ⊂= },...,{

, the aim of fuzzy clustering

is to determine the prototypes in such a way that the

objective function:

),()(),,(

∑

vxduvUXJ

is minimized (Abonyi, 2002; Menard, 2002; Bezdek,

1981), where

]1,0[

∈

stands for the membership

degree of

to the cluster i, and

),(

vxd

is the

Euclidean distance between

and the cluster i,

represented by the so called prototype

. The

apices “c” is the number of clusters. The choice of

the value of the parameter c varies from case to case.

For example, through many tests, the best

classification for right hand movement imagination

was obtained with c equal to 8, whereas for left hand

movement imagination was obtained with 6. No

theoretical foundations are yet available for the

optimal choice of the parameter of the exponent m

which was empirically set to 2.7 (Mikhailov, 1997;

Bezdek, 1981; Romdhane, 1997).

This algorithm was applied for each mental task,

so that they are represented by a set of clusters.

FCM is an iterative process in which each cluster

is regarded as a fuzzy set.

To deduce the Fuzzy rules from clusters, it is

necessary to write a membership functions for each

of them. We decided to use a triangular membership

function as a best choice for adequately represents

the clusters. This was made by projecting on each i-

th axis, the i-th coordinate of the prototype and the

two data points (trials) that are most distant from the

prototype. We assigned the minimum membership

function value (0) to the projected trials and the

maximum value of 1 to the center of the cluster

(prototype). In this way a Mamdani type fuzzy

controller was implemented (Sugeno and Yasukawa

1993; Wong, 2005).

2.2.3 Support Vector Machines

The aim of SVM is to find the hyperplane that

maximizes the separation between classes (Burges,

1998).

Let

),(

, k=1,…,m represent the training

examples for the classification problem; each

example

x ℜ∈

belongs to the class

}1,1{

−

∈

Assuming linearly separable classes, there exists a

separating hyper-plane such this:

0)( >+ bxwy

k =1,…, m (1)

),...,2,1( Cic

BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing

176

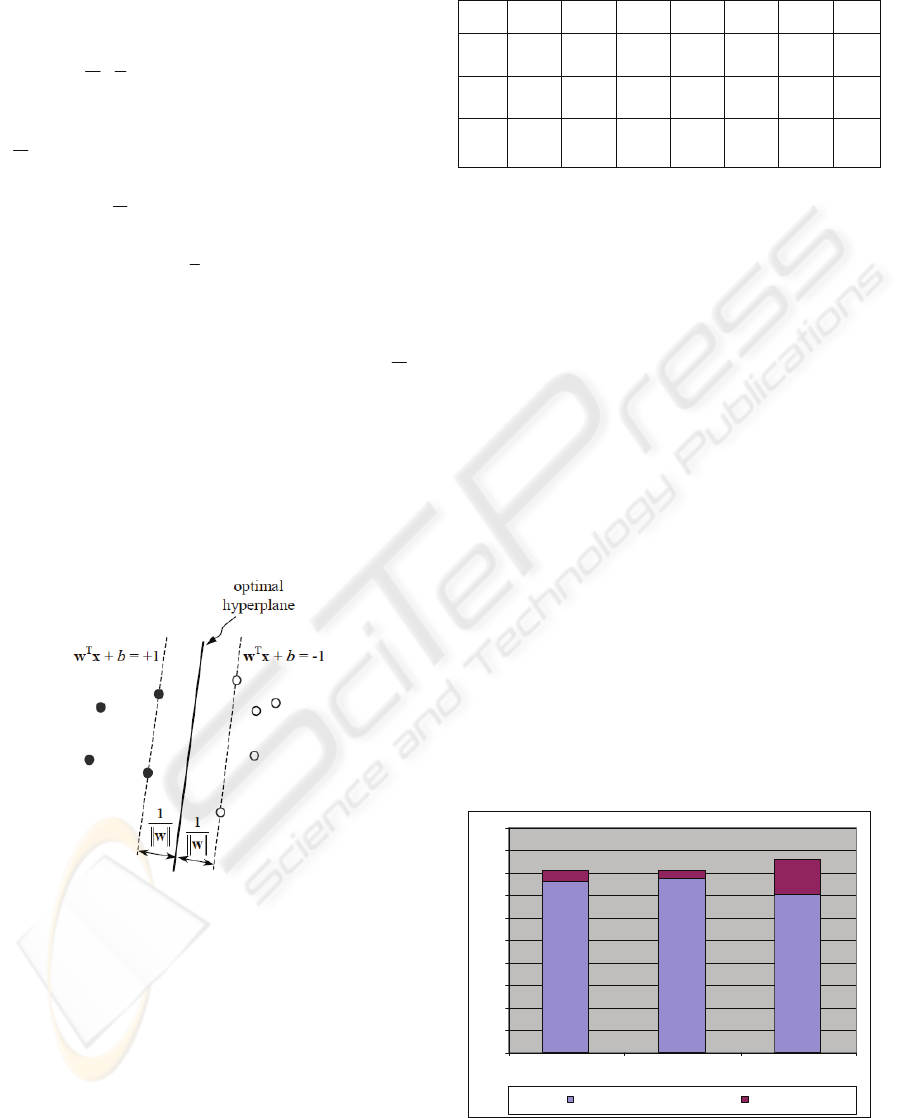
The minimum distance between the data points

and the separating hyper-plane is the margin of

separation. The goal of a SVM is to maximize this

margin. We can rescale the weights w and the bias b

so that the constraints (1) can be rewritten as

1)( ≥+ bxwy

k=1,…,m (2)

As a consequence, the margin of separation is

1/||

|| and maximization of the margin is equivalent

to the minimization of the Euclidean norm of the

weight vector

. The corresponding weights and

bias represent the optimal separating hyper-plane

(Fig. 2). The data points

for which the constraints

(2) are satisfied with the equality sign are called

support vectors.

By means of Lagrange Multipliers we are able to

consider only these vectors to find the optimal

and b (Joachims, 1999). We use a Soft Margin SVM

that introduces a tolerance to classification errors.

The tradeoff between the maximization of the

margin and the minimization of the error is

controlled by a constant C.

For our purpose we found that the best C is in the

range from 10 to 20.

Figure 2: Optimal separating hyper-plane corresponding to

the SVM solution. The support vectors lie on the dashed

lines in the caption.

3 RESULTS AND DISCUSSION

The aim of this study was to discriminate between

each possible couple of tasks. Hence 6 types of

datasets were prepared: L-R, L-S, L-N, R-S, R-N, S-

N, meaning, for instance, with L-R left and right

hand movement imagination tasks. Each dataset was

divided in training set (50% of the dataset) and test

Table 1: Mean percentage accuracies and variances on

each couple of tasks.

set (50% of the dataset).

Classification accuracies for each couple of

mental tasks are shown in table I, while, in Fig. 3,

the percentages of correct classifications as a

function of the number of training trials and for each

classifier, are reported.

It has to be noted that, from data in the literature,

the classification accuracies for these types of tasks

are not really high, being data very noisy (caused by

cerebral activity involved in other functionalities)

and because with actual means spatial resolution is

very low. This testifies that the accuracies achieved

by the three different classifiers are quite good.

As reported in the table above, MLP and fuzzy

achieve substantially the same mean accuracy

whereas SVM has a quite smaller percentage of

correct classification on some couple of tasks. But it

is important to consider that SVM presents a quite

noticeable variance in accuracy (up till 20 points on

SR and NR tasks), in fact it performs an excellent

classification on some subjects, outperforming the

two remaining classifiers.

We can then suppose that only ten electrodes

were not sufficient to stabilize the performances of

SVM on all subjects.

MLP and FCM have got a small variance and

perform a fairly good classification on all subjects.

Figure 3: Percentages of correct classifications as a

function of the number of trials in the training set.

100

MLP FCM SV M

Average Variance

SN LR SR SL NR NL

Mea

MLP 66±3 75±5 82±5 80±5 75±8 78±4 76±5

FCM 6±3 78±4 80±3 79±8 78±5 80±2

77,1

±4

SVM

60±

72±

64±

70±

73±

82±15

70,2

3±15

COMPARISON OF DIFFERENT CLASSIFIERS ON A REDUCED SET OF FEATURES FOR MENTAL

TASKS-BASED BRAIN COMPUTER INTERFACE

177

FCM achieves a good compromise between the

accuracy of classification and the computational

cost. In fact, each task required an average of 20

iterations to reach the optimum and so the learning

phase is quite faster than MLP which requires more

computational workload in learning.

Unfortunately FCM needs 40 training trials in the

clustering step to get a high accuracy compared to

MLP that uses a training set constituted by only 5

trials per task. As previously mentioned, it takes 4

seconds to record a trial, being 3 secs spent for

performing the mental task and 1 sec for the ITI.

This leads to a recording session of 80 secs for

training the MLP (5 trials x 4 tasks x 4 secs) and 640

secs for Fuzzy and SVM (40 trials x 4 tasks x 4 secs)

and so a reduction of 8 times in the training of the

former. This is critical because the training phase

should be performed every time the patient that uses

the BCI-system changed (BCI machines are ad-

personam systems), and also if the system is reused

by a different patient (in the replacement of the

helmet the electrodes position can change).

Thus the training is iterated several times and

therefore it is essential for this stage to be as fast as

possible.

4 CONCLUSIONS

It is here reported a comparison among three

different classifiers that discriminate different

mental tasks, for a BCI protocol, on a reduced set of

electrodes (features). In particular a classifier that is

not usual in the literature, based on Fuzzy logic, was

adopted.

Results demonstrate how MLP and Fuzzy

achieved the same good mean accuracy. On the

other hand the neural network needs a reduced

number of trials for training purposes, having the

advantage in the reduction of the recording session

up to 8 times with respect to the other classifiers.

The SVM method achieved different accuracies

for the best-performing subject and the worst one,

whereas with MLP and Fuzzy the variance of the

mean accuracies is quite reduced. This is important

because it attests that SVM can be not enough

accurate with noisy BCI-datasets. In any case we

considered a reduced set of features, and this could

raise the noise in the data.

By increasing the number of features we expect

that SVM improves its accuracy, performing a better

classification than other classifiers, even in the

classification of the mental calculus/recitation of

nursery rhymes couple, that, in general, is the most

difficult to discriminate.

In conclusion, from the study here reported it is

possible to deduce that MLP neural network can be

selected as the best choice for this kind of BCI

protocols, because of its good accuracy with small

variance, and because it requires a smaller number

of trials with respect to the other methods.

Performing well on a reduced set of features is of

fundamental importance, because it means that less

expensive machinery can be used, promoting the use

of BCI to enter in users’ every-day life.

ACKNOWLEDGEMENTS

This work was supported in part by the DCMC

Project of the Italian Space Agency. This paper only

reflects the authors’ views and funding agencies are

not liable for any use that may be made of the

information contained herein.

REFERENCES

Abonyi J., Babuska R. and Szeifert F., “Modified Gath-

Geva Fuzzy Clustering for Identification of Takagi-

Sugeno Fuzzy Models”, IEEE transactions on systems,

man, and cybernetics, 2002.

Allred L. G. and Kelly G. E., “Supervised learning

techniques for backpropagation networks”, IJCNN

International Joint Conference on Neural Networks,

1990, vol. 1, pp. 721-728

Bezdek J. C., “Pattern Recognition with Fuzzy Objective

Function Algorithms”, Plenum Press, 1981.

Burges C. J. C., “A tutorial on support vector machines for

pattern recognition”, Data Mining and Knowledge

Discovery 2, Kluwer, 1998, pp.121-167.

Cammarata S., “Reti neuronali, Dal perceptron alle reti

caotiche e neuro-fuzzy”, Etas 1997

Costantini G., Casali D., Carota M., Saggio G., Bianchi L.,

Abbafati M., Quitadamo L. R. “Mental Task

Recognition Based on SVM Classification”, IEEE, 3rd

IEEE International Workshop on Advances in Sensors

and Interface; 25/26 June 2009 Trani (Bari), Italy; pp.

197-200; IEEE Catalog Number: CFP09IWI-USB

ISBN: 978-1-4244-4709-1 Library of Congress:

200990484

Hara K. and Nakayamma K., “Comparison of activation

functions in multilayer neural network for pattern

classification” IEEE World Congress on

Computational Intelligence., 1994, vol. 5, pp. 2997-

3002.

Hecht-Nielsen R. “Theory of the backpropagation neural

network”, IJCNN International Joint Conference on

Neural Networks, 1989, vol.1, pp. 593-605

Hernàndez-Espinosa and Fernandez Redondo M.,

“Multilayer Feedforward Weight Initialization”,

European Symposium of Artificial Neural Networks

BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing

178

2001, pp. 119-124.

Huan N. J. and Palaniappan R., “Neural network

classification of autoregressive features from

electroencephalogram signals for brain–computer

interface design”, Journal of Neural Engineering,

2004, vol. 1, 142-150.

Joachims T., “Making large scale SVM learning

practical”, Advances in Kernel Methods-Support

Vector Learning”, B. Scholkopf, C.J.C. Burges and

A.J. Smola Eds., MIT Press, Cambridge, MA, 1999,

pp. 169-184

Kandel E., Schwartz J., and Jessell T., “Principles of

Neural Science” USA: McGraw Hill, 2000.

Lari-Najafi H., Nasiruddin M. and Samad T. “Effect of

initial weights on back-propagation and its variations”

1989, vol.1, pp. 218-219

Menard M., “Extension of the objective functions in fuzzy

clustering”, Fuzzy Systems, 2002.

Mikhailov L., Lekova A., Fischer F. and Nour Eldin H. A.,

“Method for fuzzy rules extraction from numerical

data”, IEEE International Symposium on Intelligent

Control, 1997.

Romdhane L. B., Ayeb B. and Wang S., “An improved

scheme for the fuzzifier in fuzzy clustering”, Neural

Networks for Signal Processing Proceedings of the

1997 IEEE Workshop, 1997, pp. 336-344.

Saggio G., Cavallo P., Ferretti A., Garzoli F., Quitadamo

L.R., Marciani M.G., Giannini F., Bianchi L.

“Comparison of two different classifiers for mental

tasks-based Brain-Computer Interface: MLP Neural

Networks vs. Fuzzy Logic”, 1th IEEE International

WoWMoM Workshop on Interdisciplinary Research

on E-Health Services and Systems, IREHSS 2009,

Kos (Greece) June 2009, 978-1-4244-4439-

Schögl F., Lee H., Bischof and Pfurtscheller G.,

“Characterization of four-class motor imagery EEG

data for the BCI-competition 2005”, Journal of Neural

Engineering, 2005, vol. 2, L14-L22.

Sugeno M. and Yasukawa T., “A Fuzzy Logic Based

Approach to Qualitative Modeling”, IEEE

Transactions on Fuzzy System, 1993, pp. 7-31.

Wolpaw J. R., Birbaumer N., McFarland D. J.,

Pfurtscheller G. and Vaughan T. M. "Brain-computer

interfaces for communication and control", Clinical

Neurophysiology, vol. 113, no. 6, 2002, pp. 767-791.

Wong K. W., Tikk D., Gedeon T. D. and Koczy L.T.,

“Fuzzy rule interpolation for multidimensional input

spaces with applications: a case study”, IEEE

transactions on fuzzy systems, 2005, vol. 13, no. 6.

COMPARISON OF DIFFERENT CLASSIFIERS ON A REDUCED SET OF FEATURES FOR MENTAL

TASKS-BASED BRAIN COMPUTER INTERFACE

179