
MULTIVARIATE LINEAR REGRESSION BASED SYNTHESIS
OF 12-LEAD ECG FROM THREE BIPOLAR LEADS
Ivan Tomasic, Roman Trobec and Viktor Avbelj
Department of Communication Systems, Jozef Stefan Institute, Ljubljana, Slovenia
Keywords: ECG, MECG, Multivariate Linear Regression, Synthesis, Derivation, Bipolar leads, Wireless electrodes.
Abstract: The development of new technologies for electrocardiographic (ECG) monitoring enables the optimization
of ECG recording strategy, in terms of a number and a position of body electrodes. Emerging wireless
technology, together with requirements for improved wearing comfort, dictates a special design of a
wireless bipolar ECG lead, which is composed of two closely placed electrodes. The measurements from a
set of wireless electrodes, can serve for the reconstruction of the standard 12-lead ECG, which is directly
applicable for the current medical knowledge. We present a method for synthesizing 12-lead ECG from
only three bipolar leads. The result of the proposed method, based on multivariate linear regression, is a
coefficients vector that transforms the data from three bipolar leads to a synthesized 12-leads ECG with
minimum loss of diagnostic information. Two presented test cases show that a linear combination of only
three bipolar leads, each obtained from two electrodes on a distance of 5 cm, suffices for a reliable
synthesis of a standard 12-lead ECG. Wireless ECG leads can constitute a body sensor network that
eliminates the need for additional wires and therefore improves the applicability of ECG device technology.
1 INTRODUCTION
Initial breakthrough in recording electrical activity
of the hearth came from Willem Einthoven, at the
beginning of 20
th
century. He was first to assigned
the letters to the various deflections in the
electrocardiogram (ECG), and described the
electrocardiographic features of a number of
cardiovascular disorders. Since Einthoven's time
there have been many advances in electro-
cardiography. Over the years, 12-lead ECG became
the golden standard with its diagnostic foundation
recognized by most cardiologists. The measurement
of ECG is simple and non-invasive, and therefore
widely used for diagnostic purposes in cardiology.
The conventional 12-lead ECG is obtained from
ten electrodes placed strategically on a patient's
body. The emergence of new hardware technologies
however, made possible the development of personal
and wireless ECG devices. These new technologies
impose the optimization of electrocardiographic
devices in terms of a number and a position of body
electrodes. Minimization of the required wire
lengths between electrodes and improved wearing
comfort of investigated person also became
important issues. These requirements are in partial
contradiction with the 12-lead ECG, which is the
golden standard; even that it contains an amount of
redundant information.
Several research and experimental projects have
shown (Finlay, Nugent, Kellett, Donnelly,
McCullagh, & Black, 2007) that the number of
electrodes can be reduced and their optimal placing,
that differs from the standard 12-lead ECG placing,
can be found. The measurements from reduced
electrode sets, can serve for the reconstruction (i.e.
synthesis) of the standard 12-lead ECG, which is
directly applicable for the current medical
knowledge.
There are several approaches to the introduction
of wireless technology in ECG measurements. One
of the most promising is the wireless electrode
(Valchinov & Pallikarakis, 2007) which enables the
minimal usage of wires on the body, and
consequently the maximal wearing comfort.
Since wireless electrode is bipolar (it enables the
measurements and transmission of only local
potential differences), we investigated in more
details the reconstruction of the standard 12-lead
ECG, from a set of bipolar leads with closely placed
electrodes. The distance between electrodes should
be small in order to minimize the wire length;
216
Tomasic I., Trobec R. and Avbelj V. (2010).
MULTIVARIATE LINEAR REGRESSION BASED SYNTHESIS OF 12-LEAD ECG FROM THREE BIPOLAR LEADS.
In Proceedings of the Third International Conference on Health Informatics, pages 216-221
DOI: 10.5220/0002697702160221
Copyright
c
SciTePress
however, electrodes cannot be too close because of
increased noise-to-signal ratio (Puurtinen, Viik, &
Hyttinen, 2009). Our investigation showed that a set
of only three bipolar leads, each obtained from two
electrodes on a distance of 5 cm, is sufficient for a
reliable synthesis of 12-lead ECG.
As a data source for the construction of bipolar
measurements, we used multichannel ECG (MECG)
measurements (Trobec, 2003), offering 31 unipolar
measurements. Potential differences between two
unipolar measurements were regarded as bipolar
leads. We used multivariate linear regression (MLR)
to calculate coefficients vector that transforms three
bipolar leads to the standard 12-lead ECG. For the
purpose of having minimum loss of diagnostic
information, the process is personalized in terms of
obtaining a transformation vector for each
investigated person.
2 METHODS
The 12-lead ECG is synthesized from only three
bipolar leads. Since the development of the bipolar
leads is still in an experimental phase, we emulated
them from the available MECG measurements. The
target 12-lead ECG can be reliably obtained from
MECG. Together with the emulated bipolar leads
they are used as the input data to MLR algorithm,
which computes a personalized coefficients vector
that transforms bipolar leads to a synthesized 12-
lead ECG. The target and synthesised 12-lead ECGs
can be now compared in order to evaluate the
proposed method.
2.1 Input Data
Input data sets were segments from 31-channel
MECG measurements, 10 seconds long (1000
samples/second/channel), and obtained from
different volunteers.
Currently, MECGs are mostly experimental
research devices with no common accepted standard
about the number of electrodes and their placing.
The number of MECG electrodes differs from 10 to
300 electrodes (Lux, Smith, Wyatt, & Abildskov,
1978). Their placing is mostly based on the
equidistant four neighbours mesh. We have
developed a custom MECG with 31 electrodes
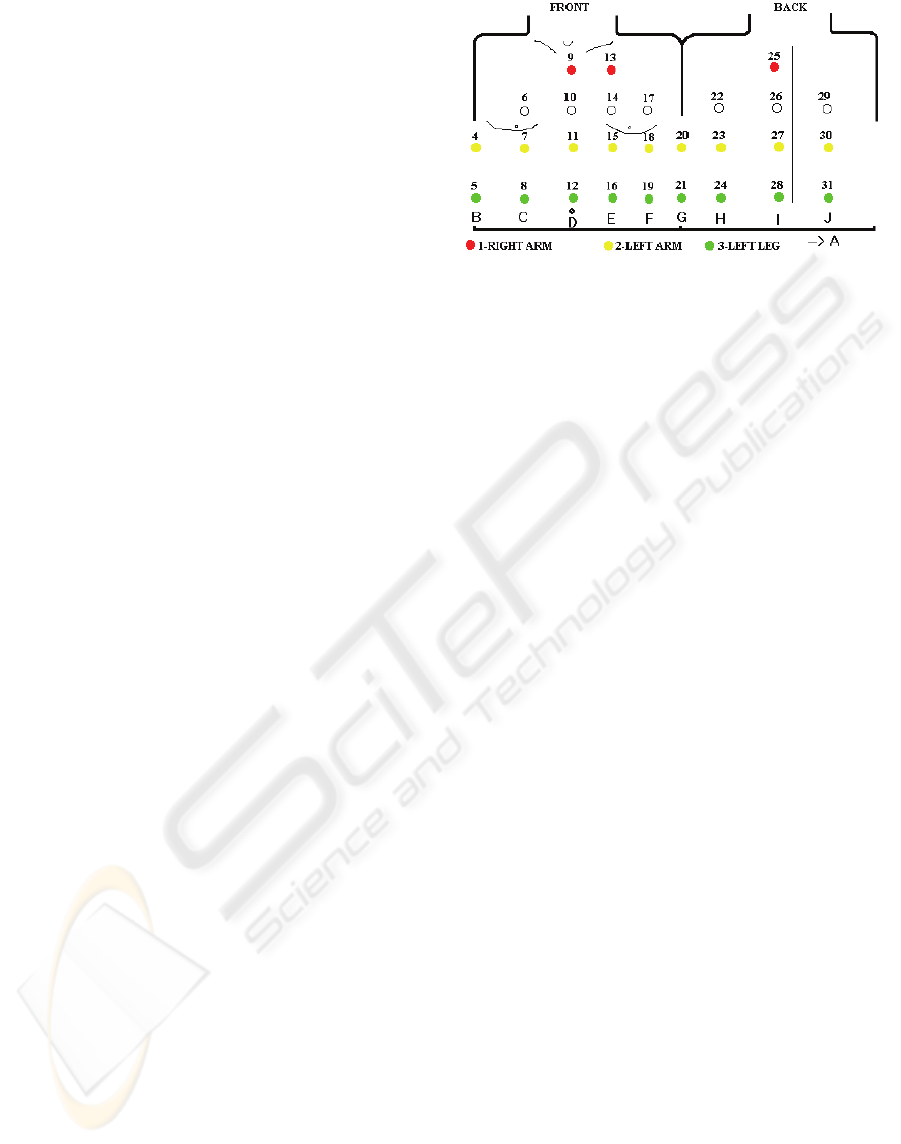
placed as shown in Figure 1, and all referenced to
the Wilson’s central terminal potential (see (Trobec,
2003) for details).
Figure 1: MECG's placement of 31 electrodes.
Note, that a MECG measurement has enough
leads, placed on appropriate positions, to exactly
reproduce the standard 12-lead ECG.
We will denote each MECG measurement in the
following way:
1
,…,
,…,
,…,,
(1)
where X(i), and X(j) are the i
th
and j
th
leads
respectively, referenced to the Wilson's central
terminal potential, and m is the total number of
leads. The Wilson's central terminal potential is an
average of limb electrodes (Okamoto & Mashima,
1998).
For an evaluation of the proposed method we
will present two test 31-channel MECG
measurements, first in a normal sinus rhythm and
second with a single supraventricular extrasystole.
Such a measurement is particularly useful because
the synthesis of the 12-lead ECG can be additionally
evaluated with the extrasystole reconstruction
ability.
2.2 Bipolar Leads
A bipolar ECG lead is composed of two connected
electrodes with appropriate electronics for
digitalization and transmission of the measured
results (Valchinov & Pallikarakis, 2007). Wireless
bipolar leads can constitute a body sensor network
that eliminates the need for additional wires and
therefore improves the applicability of mobile ECG
devices. Moreover, there is increased safety due to
the complete isolation from the power-line network
and consequently less noise. Additionally, the
influence of body movement on wireless bipolar
electrodes is much smaller than by conventional
electrodes.
A bipolar lead is a potential difference between
two unipolar electrodes i and j:
.
(2)
MULTIVARIATE LINEAR REGRESSION BASED SYNTHESIS OF 12-LEAD ECG FROM THREE BIPOLAR LEADS
217

If we denote the Wilson's central terminal potential
as φ
WCT
and subtract it from both unipolar potentials
in equation (2), we get:
,
(3)
and finally:
.
(4)
Equation (4) is used to calculate a bipolar lead from
two MECG unipolar leads.
For 31-electrode MECG from Figure 1, 465
bipolar leads can be obtained. However, bipolar
lead's wireless hardware implementation tends to
become smaller and smaller. Hence, such devices
could benefit from a small inter-electrode distance,
which restricts the set of all useful bipolar leads
from MECG, to the set of bipolar leads formed only
from nearest neighbouring electrodes. In the case of
31-electrode MECG the useful set contains just 81
bipolar leads with 85320 possible combinations of
three bipolar leads.
Since the reduction in inter-electrode distance
inevitably reduces signal strength, three bipolar
leads for synthesis of 12-lead ECG may be selected
by means of evaluating signal strength from various
bipolar leads (Puurtinen et al., 2009).
2.3 Multivariate Linear Regression
To model the relationship between a 12-lead ECG
and a set of three approximation leads we used
MLR.
First, a MECG dataset is divided into two
approximately equal intervals. Chronologically first
interval is used by MLR algorithm to calculate
transformation coefficients, and the second interval,
not known to the MLR algorithm, is used for the
estimation of algorithm's efficiency.
Let a set of three arbitrary bipolar leads from the
first interval of the MECG be denoted by:
1,2,3.
(5)
The 12-lead ECG from the first interval of the
MECG is represented as a set of 12-leads:
12,,,,,,
1,2,3,4,5,6.
(6)
As it was already mentioned, every MECG
measurement contains enough leads to exactly
reproduce the standard 12-lead ECG, so ECG12 is
produced from X (see equation (1)) and will
represent a target ECG for our approximation.
Generally, linear regression model represents the
relationship between a response (i.e. criterion
variable) ECG12 and a predictor B (Tabachnik &
Fidell, 2001, chap. 5):
12
.
(7)
The response is modelled as a linear combination of
functions (not necessarily linear) of the predictor,
plus a random error ε. The expressions f
j
(B),
(j=1,…,p) are the terms of the model while the α
j
,
(j=1,…,p) are the coefficients. Errors ε are assumed
to be uncorrelated and distributed with mean 0 and
constant, but unknown, variance. Our problem can
be solved by the multivariate regression due to the
fact that the response variable ECG12 is
multidimensional, i.e. it is composed of 12 leads
(variables).
Given n independent observations (samples):
(B
1
, ECG12
1
),…,(B
n
, ECG12
n
) of the predictor B
and the response ECG12, the linear regression
model becomes an n-by-p system of equations:
12
12
…
…
·
, or
(8)
12·,
(9)
where M is the design matrix of the system. The
columns of M are the terms of the model evaluated
at the predictors. To fit the model to the input data,
the system must be solved for the p coefficient
values: [α
1
… α
p
], by applying the least-squares
solution, i.e. by minimizing the norm of the residual
vector: ECG12-M·α. We used MATLAB "regress"
function (The MathWorks, 2009) to solve the system
from equation (9).
The predictor B is multidimensional because it is
composed of three variables, so are the functions f
j
that form the terms of the model. For three
dimensional predictor B={B
1
, B
2
, B
3
}, terms for the
model might include f
1
(B) =B
1
(or for example
f
1
(B)=B
2
), which are linear terms, f
2
(B)=B
1
2
(quadratic terms), and f
3
(B)=B
1
·B
2
(a pairwise
interaction term). Typically, the function f(B)=1 is
included among f
j
, so that the design matrix M
contains a column of ones and the model contains a
constant term.
We have explored the usage of linear additive
(straight-line) models with terms f(B) = 1 and f(B) =
HEALTHINF 2010 - International Conference on Health Informatics
218
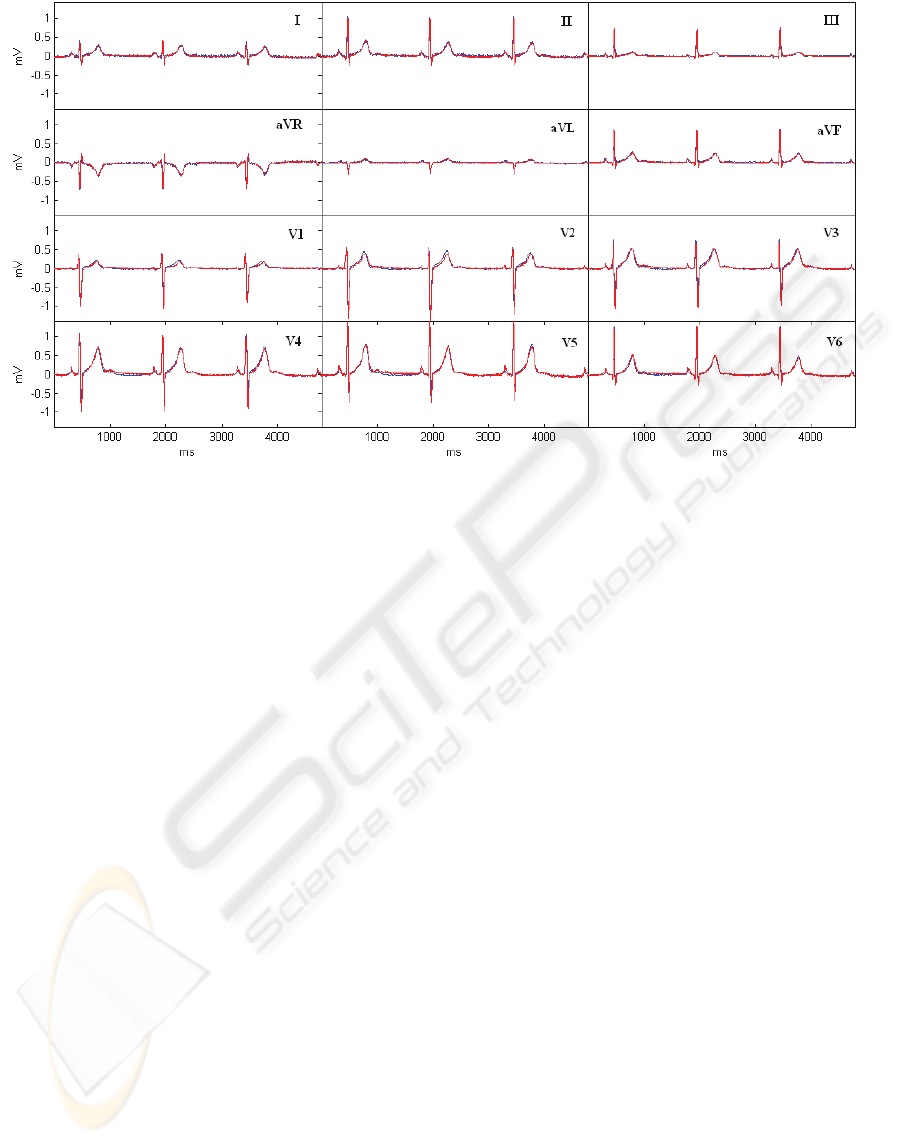
Figure 2: The target (blue) and the synthesized (red) 12-leads ECG for the first test case.
B(i). In the case of three bipolar leads, linear
additive straight-line design matrix M becomes:
1
1
2
3
1
1
2
3
,
(10)
with four coefficients in the vector α=[α
1
α
2
α
3
α
4
]
that are obtained after the system solution. If we
denote the solution coefficients by α
R
, then the result
of the M·α
R
is the best approximation of ECG12 in
the sense of the least-square solution.
Calculated transformation coefficients α
R
can be
used to synthesize 12-leads ECG from a new data,
measured on the bipolar leads for which the α
R
was
calculated.
To verify the quality of the synthesised 12-lead
ECG the second interval (not known to the
algorithm) of the input MECG is used as:
12
·
,
(11)
where M
NK
is the design matrix with bipolar leads
data from the second interval of the MECG, and
ECG12
S
is the synthesized 12-lead ECG. To verify
the quality of ECG12
S
it can be compared with the
target 12-lead ECG.
2.4 Personalization
The transformation vector for the synthesized 12-
leads ECG is personalized in a sense of being
calculated for every patient. By studying a
sufficiently large number of cases for different
patients it would be possible to calculate a global
transformation, which gives, on average, for each
individual case the best possible fit (Horacek,
Warren, Field, & Feldman, 2002). Although
possible, such an approach is not necessary due to
the fact that MECG measurement can be easily
obtained for every patient.
3 RESULTS
We will illustrate the quality of the synthesized 12-
lead ECG on two MECG datasets. For each case we
will plot the target 12-lead ECG together with the
synthesized ECG for the purpose of visually
illustrating the quality of the synthesized 12-lead
ECG. Plots shown in Figures 2 and 3 are all referred
to the second intervals of MECGs that are not
known to the MLR algorithm.
The first test case, shown in Figure 2, is a healthy
person with a normal sinus rhythm. Bipolar leads
used for the synthesis are electrode pairs: (17,15),
(11,8), (28,31). For the position of each electrode
please refer to Figure 1. The synthesized 12-lead
ECG is shown in red and the measured target ECG
in blue.
The second test case, shown in Figure 3, is a
measurement that contains, beside a normal sinus
rhythm, also a single supraventricular extrasystole.
Bipolar leads used for the synthesis, are: (13,10),
(10,15), (15,12). All other notations are the same as
MULTIVARIATE LINEAR REGRESSION BASED SYNTHESIS OF 12-LEAD ECG FROM THREE BIPOLAR LEADS
219
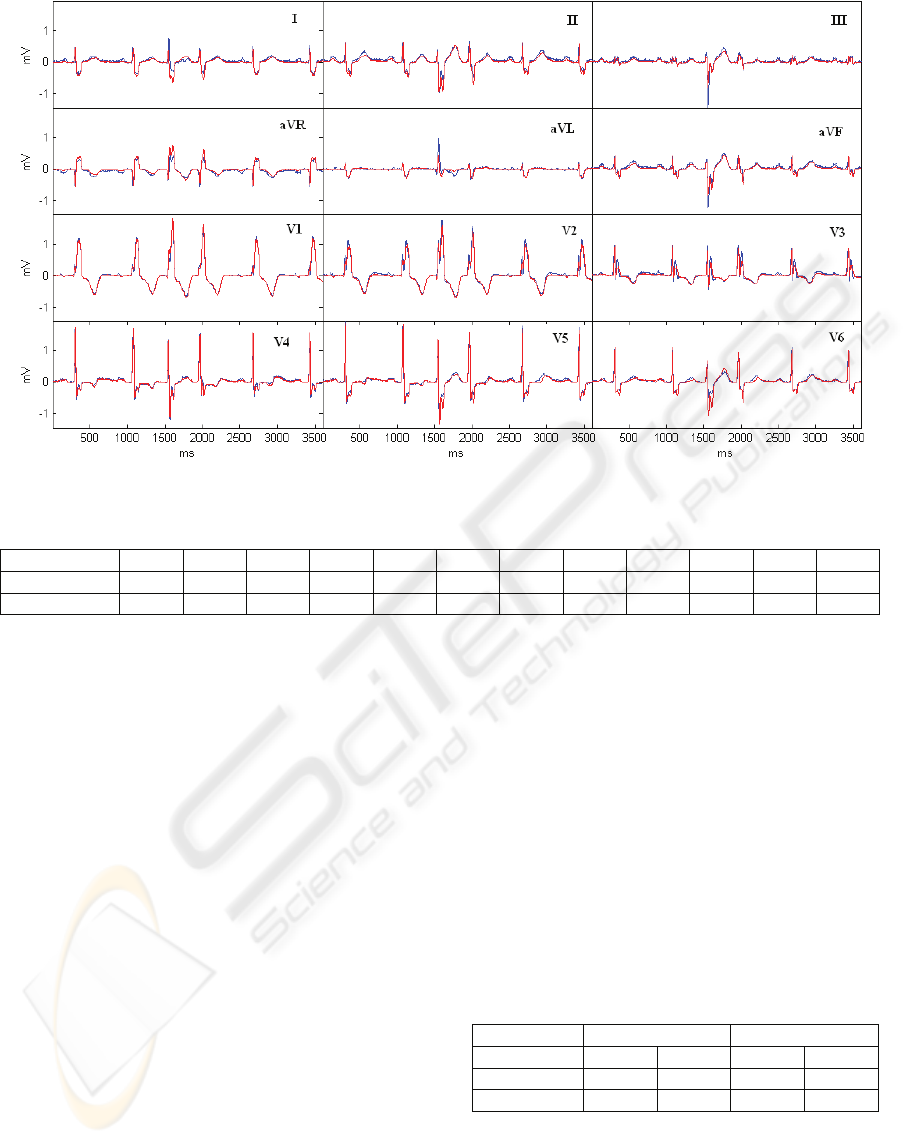
Figure 3: The target (blue) and the synthesized (red) 12-leads ECG for the second test case.
Table 1: Pearson's linear correlation coefficients between leads of synthesized and target ECG.
I II III aVR aVL aVF V1 V2 V3 V4 V5 V6
First case 0.976 0.985 0.98 0.983 0.953 0.985 0.981 0.979 0.982 0.983 0.983 0.99
Second case 0.891 0.962 0.942 0.941 0.842 0.95 0.996 0.988 0.939 0.991 0.984 0.942
in Figure 2. In this case the synthesis of the 12-lead
ECG can be additionally evaluated by the means of
the extrasystole reconstruction ability.
4 DISCUSSION
For a similarity measure between a synthesized and
a target ECG we used Pearson's linear correlation
coefficients (Kachigan, 1991, p. 130-133), which are
listed in Table 1, for all leads and for both test cases.
To investigate the differences between the two test
cases we calculated the mean (r) and standard
deviation (σ) of correlation coefficients of both test
cases, which are r
=0.98, σ1=0.009 and r
=0.947,
σ2=0.045 for the first and second test case,
respectively. The second test case is somewhat more
complex because of the extrasystole present;
therefore lower correlation coefficients have been
expected. However, visual examination of the
synthesized 12-lead ECGs reveals adequate
approximation in both test cases.
When synthesizing 12-leds ECG from
measurements obtained from electrodes placed
exclusively on patient's torso it is obviously easier to
synthesize the precordial leads than the limb leads.
To analyze the algorithm performance separately for
the limb and precordial leads we can calculate the
mean and standard deviations of correlation
coefficients separately as shown in Table 2.
The correlation results are somewhat better for
the precordial leads in both test cases as it was
expected. Nevertheless, the algorithm produces
synthesized 12-lead ECG with significant
correlations on limb and precordial leads in both test
cases. The definite diagnostic value of the
synthesized 12-lead ECG is left to be confirmed by
further experiments and their interpretation by
cardiologists.
Table 2: Mean and standard deviation of Pearson's linear
correlation coefficients for the limb and precordial leads.
Limb leads Precordial leads
mean st. dev. mean st. dev.
First case 0.977 0.012 0.983 0.004
Second case 0.921 0.046 0.973 0.026
5 CONCLUSIONS
The ECG monitoring is routinely useful in the early
HEALTHINF 2010 - International Conference on Health Informatics
220

detection of life threatening events. Currently
available medical instrumentation however, shows
limited abilities for continues, long-term ECG
monitoring. One of the key limitations of mobile
ECG devices (like Holter monitors) is a limited
number of lead measurements that they produce.
We have proposed a way to synthesize 12-lead
ECG from a small set of bipolar leads composed of
two electrodes with a distance of 5 cm. We emulated
bipolar measurements from 31 unipolar MECG's
leads. From the same MECG measurement the target
12-lead ECG is calculated and used, together with
three bipolar leads, as the inputs for MLR algorithm.
The MLR algorithm generates a coefficients vector
that transforms three bipolar leads to a synthesized
12-lead ECG.
We evaluated the quality of synthesized ECGs
on two test cases by visual comparison and by
analysing Pearson's linear correlation coefficient
calculated between the target and synthesized 12-
lead ECGs.
In the further work, we plan to evaluate and
verify the proposed approach on more test cases in
order to confirm its diagnostic value. The wireless
bipolar electrodes will be applied for the direct
bipolar measurement on patient's body. The
proposed methodology is widely applicable to the
emerging wireless body sensors technology because
it increases patient’s mobility and comfort.
ACKNOWLEDGEMENTS
This research was funded under Grant No. P2-0095
by the Ministry of Higher Education, Science and
Technology of Slovenia.
REFERENCES
Finlay, D. D., Nugent, C. D., Kellett, J. G., Donnelly, M.
P., McCullagh, P. J., & Black, N. D. (2007).
Synthesising the 12-lead electrocardiogram: Trends
and challenges. European Journal of Internal
Medicine , 18, 566–570.
Horacek, B. M., Warren, J. W., Field, D. Q., & Feldman,
C. L. (2002). Statistical and Deterministic Approaches
to Designing Transformations of Electrocardiographic
Leads. Jurnal of Electrocardiology , 22 (Supp.).
Kachigan, S. K. (1991). Multivariate Statistical Analysis
(A Conceptual Introduction) (2nd ed.). Radius Press.
Lux, R. L., Smith, C. R., Wyatt, R. F., & Abildskov, J. A.
(1978). Limited Lead Selection for Estimation of
Body Surface Potential Maps in Electrocardiography.
IEEE Trans. Biomed. Eng. , 25 (3), 270–276.
Okamoto, Y., & Mashima, S. (1998). The zero potential
and Wilson’s central terminal in electrocardiography.
Bioelectrochemistry and Bioenergetics , 47, 291–295.
Puurtinen, M., Viik, J., & Hyttinen, J. (2009). Best
Electrode Locations for a Small Bipolar ECG Device:
Signal Strength Analysis of Clinical Data. Annals of
Biomedical Engineering , 37 (2), 331-336.
(2001). Multiple Regression. In B. G. Tabachnik, & L. S.
Fidell, Using Multivariate Statistics (4th ed., pp. 111-
176). Allyn and Bacon.
(2009). Statistical Toolbox. In I. The MathWorks,
MATLAB documentation.
Trobec, R. (2003). Computer analysis of multichannel
ECG. Computers in Biology and Medicine , 33, 215-
226.
Valchinov, E. S., & Pallikarakis, N. E. (2007). Wearable
Wireless Biopotential Electrode for ECG Monitoring.
IFMBE Proceedings 16 (pp. 373–376). Springer-
Verlag.
MULTIVARIATE LINEAR REGRESSION BASED SYNTHESIS OF 12-LEAD ECG FROM THREE BIPOLAR LEADS
221
