PARACONSISTENT NEGATION AND CLASSICAL NEGATION

IN COMPUTATION TREE LOGIC

Norihiro Kamide

Waseda Institute for Advanced Study, 1-6-1 Nishi Waseda, Shinjuku-ku, Tokyo 169-8050, Japan

Ken Kaneiwa

National Institute of Information and Communications Technology, 3-5 Hikaridai, Seika, Soraku, Kyoto 619-0289, Japan

Keywords:

Computation tree logic, Paraconsistent logic, Decidability, Medical reasoning.

Abstract:

A paraconsistent computation tree logic, PCTL, is obtained by adding paraconsistent negation to the standard

computation tree logic CTL. PCTL can be used to appropriately formalize inconsistency-tolerant temporal

reasoning. A theorem for embedding PCTL into CTL is proved. The validity, satisﬁability, and model-

checking problems of PCTL are shown to be decidable. The embedding and decidability results indicate that

we can reuse the existing CTL-based algorithms for validity, satisﬁability and model-checking. An illustrative

example of medical reasoning involving the use of PCTL is presented.

1 INTRODUCTION

Computation tree logic (CTL) (Clarke and Emerson,

1981) is known to be one of the most useful tempo-

ral logics for verifying concurrent systems by model

checking (Clarke et al., 1999), since some CTL-based

model checking algorithms are more efﬁcient than

other types of algorithms. However, the use of CTL

is not suitable for verifying “inconsistent” concurrent

systems since CTL is based on classical logic. Han-

dling inconsistencies in concurrent systems requires

the use of a paraconsistent logic (Beziau, 1999; Priest

and Routley, 1982) as a base logic for CTL.

One of the most useful paraconsistent logics is

Nelson’s four-valued paraconsistent logic N4 (or also

called N

−

) (Almukdad and Nelson, 1984; Nelson,

1949), which includes a paraconsistent negation con-

nective. The logic N4 and its variants have been stud-

ied by many researchers (see, e.g., (Wagner, 1991;

Wansing, 1993) and the references therein). N4 has

been extensively studied since it has the property of

paraconsistency (Beziau, 1999; da Costa et al., 1995;

Priest and Routley, 1982). Roughly, a satisfaction re-

lation |= is said to be paraconsistent with respect to

a negation connective ∼ if the following condition

holds: ∃α,β, not-[M,s |= (α ∧ ∼α)→β], where s is a

state of a Kripke structure M. In contrast to N4, classi-

cal logic has no paraconsistency because the formula

of the form (α∧ ∼α)→β is valid in classical logic.

It is known that paraconsistent logical systems

are more appropriate for inconsistency-tolerant and

uncertainty reasoning than other types of logical

systems (Beziau, 1999; da Costa et al., 1995;

Priest and Routley, 1982; Wagner, 1991; Wansing,

1993). For example, the following scenario is un-

desirable (s(x) ∧ ∼s(x))→d(x) is satisﬁed for any

symptom s and disease d where ∼s(x) means “a

person x does not have a symptom s” and d(x)

means “a person x suffers from a disease d.” An

inconsistent scenario expressed, for example, as

melancholia( john) ∧ ∼melancholia( john) will in-

evitably occur, because melancholia is an uncer-

tain concept and the fact “John has melancholia”

may be determined to be true or false by differ-

ent pathologists with different perspectives. In this

case, the undesirable formula (melancholia( john) ∧

∼melancholia( john))→cancer( john) is valid in

classical logic (i.e., an inconsistency has undesirable

consequences), while it is not valid in paraconsistent

logics (i.e., these logics are inconsistency-tolerant).

Inconsistencies often appear and are inevitable

when specifying large, complex systems in some

CTL-based frameworks. N4 is then useful and ap-

propriate as a base logic for CTL. Moreover, N4 has

notable two consequence relations |=

(veriﬁcation)

and |=

−

(refutation) in the Kripke semantics. By us-

464

Kamide N. and Kaneiwa K. (2010).

PARACONSISTENT NEGATION AND CLASSICAL NEGATION IN COMPUTATION TREE LOGIC.

In Proceedings of the 2nd International Conference on Agents and Artiﬁcial Intelligence - Artiﬁcial Intelligence, pages 464-469

DOI: 10.5220/0002699504640469

 SciTePress

ing these consequence relations, the ideas of “veri-

ﬁcation (or justiﬁcation)” and “refutation (or falsiﬁ-

cation)” can be simultaneously incorporated into the

system. Therefore, the combination of CTL and N4 is

regarded as a natural candidate for obtaining a useful

paraconsistent temporal logic.

In this paper, a new paraconsistent computation

tree logic called PCTL is introduced by combining

CTL and N4. While the idea of combining CTL

and N4 is new, the idea of introducing a paracon-

sistent computation tree logic is not. For example,

a multi-valued computation tree logic χCTL was in-

troduced by Easterbrook and Chechik (Easterbrook

and Chechik, 2001), and a quasi-classical temporal

logic QCTL was developed by Chen and Wu (Chen

and Wu, 2006). Thus, PCTL is introduced as an alter-

native to these logics, and N4 replaces the base para-

consistent logic.

As mentioned above, the application for which

paraconsistent logics show the greatest promise may

be medical informatics. Indeed, it has been pointed

out that paraconsistent logics are useful for medical

reasoning (see, e.g., (da Costa et al., 1995; Murata

et al., 1991) and the references therein). Some para-

consistent computation tree logics, including PCTL,

may be more useful in medical informatics because

the notion of time is necessary in order to appropri-

ately formalize realistic medical reasoning. Against

this background, we present an illustrative example of

medical reasoning. The proposed illustrative example

can also be adapted to other paraconsistent computa-

tion tree logics such as χCTL and QCTL.

2 PARACONSISTENT

COMPUTATION TREE LOGIC

Formulas of PCTL are constructed from countable

atomic formulas, → (implication) ∧ (conjunction), ∨

(disjunction), ¬ (classical negation), ∼ (paraconsis-

tent negation), X (next), G (globally), F (eventually),

U (until), R (release), A (all computation paths) and

E (some computation path). The symbols X, G, F,

U and R are called temporal operators, and the sym-

bols A and E are called path quantiﬁers. The symbol

ATOM is used to denote the set of atomic formulas.

An expression A ≡ B is used to denote the syntactical

identity between A and B.

Deﬁnition 2.1. Formulas α are deﬁned by the follow-

ing grammar, assuming p ∈ ATOM:

α ::= p | α→α | α ∧ α | α∨ α | ¬α | ∼α |

AXα | EXα | AGα | EGα | AFα | EFα |

A(αUα) | E(αUα) | A(αRα) | E(αRα).

Note that pairs of symbols like AG and EU are in-

divisible, and that the symbols X,G,F,U and R can-

not occur without being preceded by an A or an E.

Similarly, every A or E must have one of X, G, F, U

and R to accompany it. Remark that all the connec-

tives displayed above are needed to obtain an embed-

ding theorem of PCTL into CTL.

Deﬁnition 2.2. A paraconsistent Kripke structure is a

structure hS,S

,R,L

−

i such that

1. S is the set of states,

2. S

is a set of initial states and S

⊆ S,

3. R is a binary relation on S which satisﬁes the con-

dition: ∀s ∈ S ∃s

′

∈ S [(s,s

′

) ∈ R],

4. L

and L

−

are functions from S to the power set

of a nonempty subset AT of ATOM.

A path in a paraconsistent Kripke structure is an

inﬁnite sequence of states, π = s

,... such that

∀i ≥ 0 [(s

i+1

) ∈ R].

The logic PCTL is then deﬁned as a paraconsis-

tent Kripke structure with two satisfaction relations

and |=

−

. The intuitive meanings of |=

and |=

−

are “veriﬁcation (or justiﬁcation)” and “refutation (or

falsiﬁcation)”, respectively (Wansing, 1993).

Deﬁnition 2.3. Let AT be a nonempty subset of

ATOM. Satisfaction relations |=

and |=

−

on a para-

consistent Kripke structure M = hS,S

,R,L

−

i are

deﬁned inductively as follows (s represents a state in

S):

1. for any p ∈ AT, M,s |=

p iff p ∈ L

(s),

2. M,s |=

→α

iff M,s |=

implies M, s |=

3. M,s |=

∧ α

iff M,s |=

and M,s |=

4. M,s |=

∨ α

iff M,s |=

or M,s |=

5. M,s |=

¬α

iff not-[M,s |=

6. M,s |=

∼α iff M,s |=

−

α,

7. M,s |=

AXα iff ∀s

∈ S [(s,s

) ∈ R implies

M,s

α],

8. M,s |=

EXα iff ∃s

∈ S [(s,s

) ∈ R and

M,s

α],

9. M,s |=

AGα iff for all paths π ≡ s

,...,

where s ≡ s

, and all states s

along π, we have

M,s

α,

10. M, s |=

EGα iff there is a path π ≡ s

,...,

where s ≡ s

, and for all states s

along π, we have

M,s

α,

11. M, s |=

AFα iff for all paths π ≡ s

,...,

where s ≡ s

, there is a state s

along π such that

M,s

α,

12. M, s |=

EFα iff there is a path π ≡ s

,...,

where s ≡ s

, and for some state s

along π, we

have M,s

α,

PARACONSISTENT NEGATION AND CLASSICAL NEGATION IN COMPUTATION TREE LOGIC

465

13. M,s |=

A(α

Uα

) iff for all paths π ≡

,..., where s ≡ s

, there is a state s

along

π such that [(M,s

) and ∀ j (0 ≤ j < k im-

plies M,s

)],

14. M,s |=

E(α

Uα

) iff there is a path π ≡

,..., where s ≡ s

, and for some state s

along π, we have [(M, s

) and ∀ j (0 ≤ j <

k implies M, s

)],

15. M,s |=

A(α

Rα

) iff for all paths π ≡

,..., where s ≡ s

, and all states s

along

π, we have [∀i < j not-[M, s

] implies

M,s

16. M,s |=

E(α

Rα

) iff there is a path π ≡

,..., where s ≡ s

, and for all states s

along π, we have [∀i < j not-[M,s

] im-

plies M,s

17. for any p ∈ AT, M, s |=

−

p iff p ∈ L

−

(s),

18. M,s |=

−

→α

iff M,s |=

and M,s |=

−

19. M,s |=

−

∧ α

iff M,s |=

−

or M,s |=

−

20. M,s |=

−

∨ α

iff M, s |=

−

and M,s |=

−

21. M,s |=

−

¬α

iff M,s |=

22. M,s |=

−

∼α

iff M,s |=

23. M,s |=

−

AXα iff ∃s

∈ S [(s,s

) ∈ R and

M,s

−

α],

24. M,s |=

−

EXα iff ∀s

∈ S [(s,s

) ∈ R implies

M,s

−

α],

25. M,s |=

−

AGα iff there is a path π ≡ s

,...,

where s ≡ s

, and for some state s

along π, we

have M,s

−

α,

26. M,s |=

−

EGα iff for all paths π ≡ s

,...,

where s ≡ s

, there is a state s

along π such that

M,s

−

α,

27. M,s |=

−

AFα iff there is a path π ≡ s

,...,

where s ≡ s

, and for all states s

along π, we have

M,s

−

α,

28. M,s |=

−

EFα iff for all paths π ≡ s

,...,

where s ≡ s

, and all states s

along π, we have

M,s

−

α,

29. M,s |=

−

A(α

Uα

) iff there is a path π ≡

,..., where s ≡ s

, and for all states s

along π, we have [∀i < j not-[M,s

−

] im-

plies M,s

−

30. M,s |=

−

E(α

Uα

) iff for all paths π ≡

,..., where s ≡ s

, and for all states s

along π, we have [∀i < j not-[M,s

−

] im-

plies M,s

−

31. M,s |=

−

A(α

Rα

) iff there is a path π ≡

,..., where s ≡ s

, and for some state s

along π, we have [(M, s

−

) and ∀ j (0 ≤ j <

k implies M, s

−

)],

32. M, s |=

−

E(α

Rα

) iff for all paths π ≡

,..., where s ≡ s

, there is a state s

along

π such that [(M, s

−

) and ∀ j (0 ≤ j < k im-

plies M,s

−

)].

Deﬁnition 2.4. A formula α is valid (satisﬁable)

in PCTL if and only if M,s |=

α holds for

any (some) paraconsistent Kripke structure M =

hS,S

,R,L

−

i, any (some) s ∈ S, and any (some)

satisfaction relations |=

and |=

−

on M.

Deﬁnition 2.5. Let M be a paraconsistent Kripke

structure hS,S

,R,L

−

i for PCTL, and |=

and |=

−

be satisfaction relations on M. Then, the positive and

negative model checking problems for PCTL are re-

spectively deﬁned by: for any formula α, ﬁnd the sets

{s ∈ S | M, s |=

α} and {s ∈ S | M,s |=

−

α}.

An expression α ↔ β is used to represent

(α→β) ∧ (β→α).

Proposition 2.6. The following formulas concerning

paraconsistent negation are valid in PCTL: for any

formulas α and β,

1. ∼∼α ↔ α,

2. ∼(α∧β) ↔ ∼α∨ ∼β,

3. ∼(α∨β) ↔ ∼α∧ ∼β,

4. ∼(α→β) ↔ α∧ ∼β,

5. ∼¬α ↔ α,

6. ∼AXα ↔ EX∼α,

7. ∼EXα ↔ AX∼α,

8. ∼AGα ↔ EF∼α,

9. ∼EGα ↔ AF∼α,

10. ∼AFα ↔ EG∼α,

11. ∼EFα ↔ AG∼α,

12. ∼A(αUβ) ↔ E((∼α)R(∼β)),

13. ∼E(αUβ) ↔ A((∼α)R(∼β)),

14. ∼A(αRβ) ↔ E((∼α)U(∼β)),

15. ∼E(αRβ) ↔ A((∼α)U(∼β)).

For each s ∈ S and each formula α, we can take

one of the following four cases: (1) α is veriﬁed at

s, i.e., M,s |=

α, (2) α is falsiﬁed at s, i.e., M,s |=

−

α, (3) α is both veriﬁed and falsiﬁed at s, and (4) α

is neither veriﬁed nor falsiﬁed at s. Thus, PCTL is

regarded as a four-valued logic.

Assume a paraconsistent Kripke structure M =

hS,S

,R,L

−

i such that p ∈ L

(s), p ∈ L

−

(s) and

q /∈ L

(s) for any distinct atomic formulas p and q.

Then, M, s |=

(p∧ ∼p)→q does not hold, and hence

in PCTL is paraconsistent with respect to ∼.

In order to deﬁne a translation of PCTL into CTL,

CTL is deﬁned below.

Deﬁnition 2.7 (CTL). A Kripke structure for CTL is

a structure hS,S

,R,Li such that

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

466

1. S is the set of states,

2. S

is a set of initial states and S

⊆ S,

3. R is a binary relation on S which satisﬁes the con-

dition: ∀s ∈ S ∃s

′

∈ S [(s,s

′

) ∈ R],

4. L is a function from S to the power set of a

nonempty subset AT of ATOM.

A satisfaction relation |= on a Kripke structure M =

hS,S

,R,Li for CTL is deﬁned by the same conditions

1–5 and 7–16 as in Deﬁnition 2.3 (by deleting the su-

perscript +). The validity, satisﬁability and model-

checking problems for CTL are deﬁned similarly as

those for PCTL.

Remark that |=

of PCTL includes |= of CTL, and

hence PCTL is an extension of CTL.

3 EMBEDDING AND

DECIDABILITY

In the following, we introduce a translation of PCTL

into CTL, and by using this translation, we show

an embedding theorem of PCTL into CTL. A simi-

lar translation has been used by Gurevich (Gurevich,

1977), Rautenberg (Rautenberg, 1979) and Vorob’ev

(Vorob’ev, 1952) to embed Nelson’s three-valued

constructive logic (Almukdad and Nelson, 1984; Nel-

son, 1949) into intuitionistic logic.

Deﬁnition 3.1. Let AT be a non-empty subset of

ATOM, and AT

′

be the set {p

′

| p ∈ AT} of atomic

formulas. The language L

∼

(the set of formulas) of

PCTL is deﬁned using AT, ∼, ¬,→,∧,∨, X, F, G, U,

R, A and E. The language L of CTL is obtained from

∼

by adding AT

′

and deleting ∼.

A mapping f from L

∼

to L is deﬁned inductively

by:

1. for any p ∈ AT, f(p) := p and f(∼p) := p

′

∈ AT

′

2. f(α ♯ β) := f(α) ♯ f(β) where ♯ ∈ {∧,∨,→},

3. f(♯α) := ♯ f(α) where ♯ ∈ {¬,AX,EX, AG,EG,

AF,EF},

4. f(A(αUβ))) := A( f(α)Uf (β)),

5. f(E(αUβ))) := E( f (α)Uf(β)),

6. f(A(αRβ))) := A( f(α)Rf (β)),

7. f(E(αRβ))) := E( f(α)Rf(β)),

8. f(∼ ∼α) := f(α),

9. f(∼ (α→β)) := f(α) ∧ f(∼β),

10. f(∼(α∧ β)) := f(∼α) ∨ f(∼β),

11. f(∼(α∨ β)) := f(∼α) ∧ f(∼β),

12. f(∼¬α) := f(α),

13. f(∼AXα) := EXf (∼α),

14. f(∼EXα) := AXf (∼α),

15. f(∼AGα) := EFf(∼α),

16. f(∼EGα) := AFf(∼α),

17. f(∼AFα) := EGf(∼α),

18. f(∼EFα) := AGf(∼α),

19. f(∼(A(αUβ))) := E( f(∼α)Rf(∼β)),

20. f(∼(E(αUβ))) := A( f(∼α)Rf(∼β)),

21. f(∼(A(αRβ))) := E( f (∼α)Uf(∼β)),

22. f(∼(E(αRβ))) := A( f (∼α)Uf(∼β)).

Lemma 3.2. Let f be the mapping deﬁned in Deﬁ-

nition 3.1. For any paraconsistent Kripke structure

M := hS,S

,R,L

−

i for PCTL, and any satisfac-

tion relations |=

and |=

−

on M, there exist a Kripke

structure N := hS, S

,R,Li for CTL and a satisfaction

relation |= on N such that for any formula α in L

∼

and any state s in S,

1. M,s |=

α iff N, s |= f(α),

2. M,s |=

−

α iff N, s |= f(∼α).

Proof. Suppose that M is a paraconsistent Kripke

structure hS,S

,R,L

−

i such that L

and L

−

are

functions from S to the power set of AT. Suppose that

N is a Kripke structure M := hS,S

,R,Li such that L

is a function from S to the power set of AT∪AT

′

. Sup-

pose moreover that for any s ∈ S and any p ∈ AT, (1):

p ∈ L

(s) iff p ∈ L(s) and (2): p ∈ L

−

(s) iff p

′

∈ L(s).

The lemma is then proved by (simultaneous) in-

duction on the complexity of α. The base step is ob-

vious. We show some cases for the induction step.

Case α ≡ ∼β: For (1), we obtain: M, s |=

∼β iff

M,s |=

−

β iff N,s |= f(∼ β) (by induction hypothesis

for 2). For (2), we obtain: M,s |=

−

∼β iff M,s |=

β iff N,s |= f (β) (by induction hypothesis for 1) iff

N,s |= f(∼∼β) (by the deﬁnition of f).

Case α ≡ A(βUγ): For (1), we obtain:

M,s |=

A(βUγ)

iff for all paths π ≡ s

,..., where s ≡ s

, there is

a state s

along π such that [M,s

γ and ∀ j[i ≤

j < k implies M,s

β]

iff for all paths π ≡ s

,..., where s ≡ s

, there

is a state s

along π such that [N, s

|= f(γ) and

∀ j[i ≤ j < k implies N,s

|= f(β)] (by induction

hypothesis for 1)

iff N,s |= A( f(β)Uf(γ))

iff N,s |= f(A(βUγ)) (by the deﬁnition of f).

For (2), we obtain:

M,s |=

−

A(βUγ)

iff there is a path π ≡ s

,..., where s ≡ s

, and

for all states s

along π, we have [∀i < j not-

[M,s

−

β] implies M,s

−

γ]

PARACONSISTENT NEGATION AND CLASSICAL NEGATION IN COMPUTATION TREE LOGIC

467

iff there is a path π ≡ s

,..., where s ≡ s

, and

for all states s

along π, we have [∀i < j not-

[N,s

|= f(∼β)] implies N,s

|= f(∼γ)] (by induc-

tion hypothesis for 2)

iff N,s |= E( f(∼β)Rf(∼γ))

iff N,s |= f(∼(A(βUγ))) (by the deﬁnition of f).

Lemma 3.3. Let f be the mapping deﬁned in Deﬁni-

tion 3.1. For any Kripke structure N := hS,S

,R,Li

for CTL, and any satisfaction relation |= on N,

there exist a paraconsistent Kripke structure M :=

hS,S

,R,L

−

i for PCTL and satisfaction relations

and |=

−

on M such that for any formula α in L

∼

and any state s in S,

1. N, s |= f(α) iff M, s |=

α,

2. N, s |= f(∼α) iff M,s |=

−

α.

Proof. Similar to the proof of Lemma 3.2.

Theorem 3.4 (Embedding). Let f be the mapping

deﬁned in Deﬁnition 3.1. For any formula α, α is

valid in PCTL iff f(α) is valid in CTL.

Proof. By Lemmas 3.2 and 3.3.

Theorem 3.5 (Decidability). The model-checking,

validity and satisﬁability problems for PCTL are de-

cidable.

Proof. By f in Deﬁnition 3.1, a formula α of PCTL

can ﬁnitely be transformed into the correspondingfor-

mula f(α) of CTL. By Lemmas 3.2 and 3.3 and The-

orem 3.4, the model checking, validity and satisﬁabil-

ity problems for PCTL can be transformed into those

of CTL. Since the model checking, validity and sat-

isﬁability problems for CTL are decidable, the prob-

lems for PCTL are also decidable.

4 ILLUSTRATIVE EXAMPLE

We now consider examples of state structures for

representing the health of non-smokers and smok-

ers, as shown in Figure 1. In the state structure,

the medical state of a person is described in a de-

cision diagram where branching-tree structures and

negative connectives from PCTL are employed. In

this example, a paraconsistent negation ∼α in PCTL

is used to express the negation of ambiguous con-

cepts. For instance, if we cannot determine whether

someone is healthy, the ambiguous concept healthy

can be represented by asserting the inconsistent for-

mula healthy∧∼healthy. This is well formalized be-

cause (healthy∧ ∼healthy)→⊥ is not valid in para-

consistent logic. On the other hand, we can decide

whether someone is smoking; the decision is repre-

sented by smoking or ¬smoking, where (smoking ∧

¬smoking)→⊥ is valid in classical logic.

In Figure 1, the initial state implies that a person

is not smoking (¬smoking is true). The system can

move to the other state to indicate that the person is

smoking (smoking is true). When a person under-

goes a medical checkup, his or her state changes to

one of the two states. Even if no cancer is detected

in a smoker during the medical checkup, he or she is

both healthy and not healthy, i.e., both healthy and

∼healthy are true because smoking is detrimental to

health. If cancer is detected (hasCancer is true) in a

non-smoker (or smoker), then ∼healthy is true. This

means that the person is not healthy, but he or she may

return to good health if the cancer does not increase.

In these states, ∼healthy represents ambiguous nega-

tive information that can be true at the same time as

healthy, which represents positive information

Moreover, when the cancer increases, the diagno-

sis reveals worse cancer. If the cancer is cured, the

patient will be healthy. Otherwise, if the cancer is not

controlled, the patient will die.

We deﬁne a Kripke structure M =

hS,S

,R,L

−

i that corresponds to the medi-

cal state structure as follows:

1. S = {s

2. S

= {s

3. R = {(s

),(s

)},

4. L

) =

5. L

) = {smoking},

6. L

) = {healthy},

7. L

) = {hasCancer},

8. L

) = {healthy},

9. L

) = {cancerIncrease,hasCancer},

10. L

) = {died, hasCancer} ,

11. L

−

) = L

−

) = L

−

) = L

−

) = L

−

) =

12. L

−

) = L

−

) = {healthy}.

We can verify the existence of a path that rep-

resents the required information in the structure M.

For example, we can verify the following statement:

“Is there a state in which a person is both healthy

and not healthy?” This statement is expressed as:

EF(healthy∧ ∼healthy). The above statement is true

because we have a path s

→s

where healthy ∈

) and healthy ∈ L

−

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

468

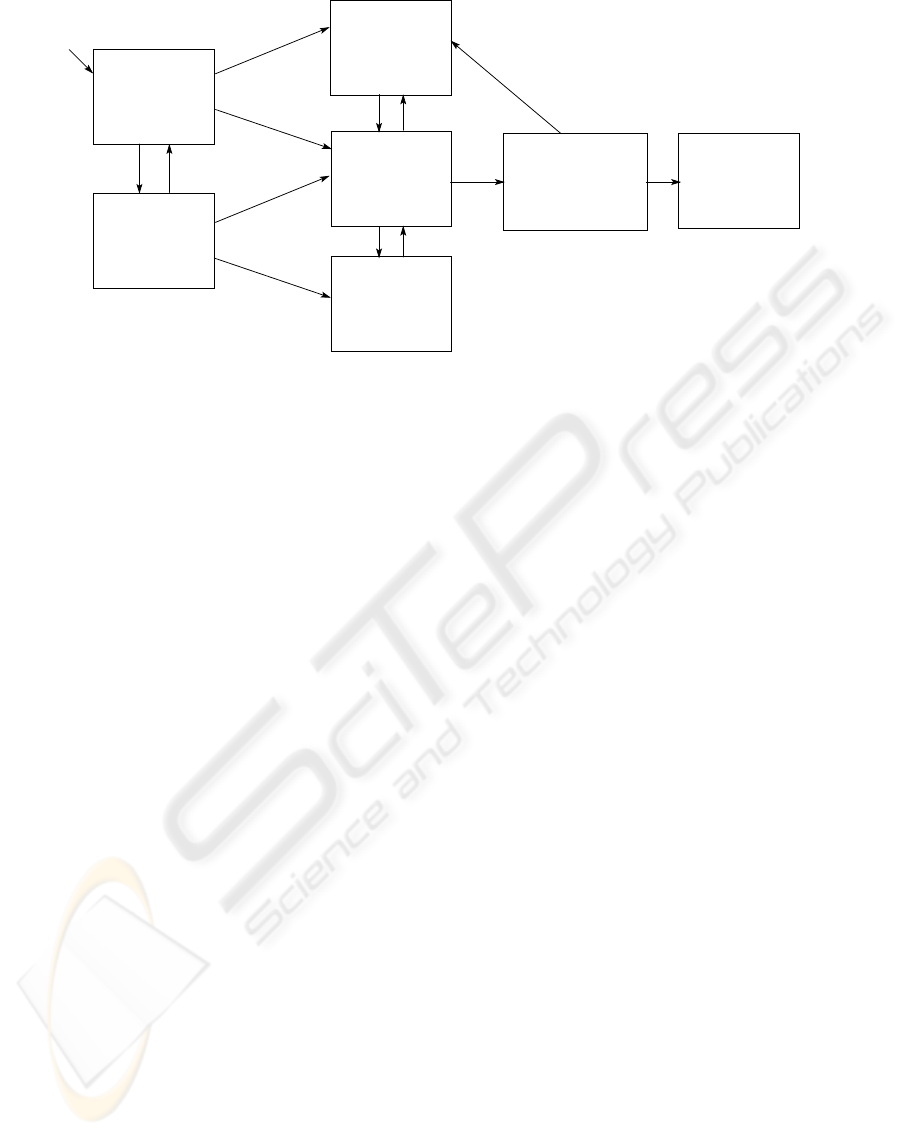
healthy

¬smoking

smoking

∼healthy

healthy

cured

died

cancerIncrease

hasCancer

medicalCheckup

continuing continuing

¬hasCancer

hasCancer

Figure 1: State structure for representing the health of smokers and non-smokers.

5 CONCLUSIONS

A new paraconsistent computation tree logic, PCTL,

was introduced by combiningCTL and Nelson’s para-

consistent logic N4. This logic could be used appro-

priately in medical reasoning to deal with inconsistent

data and uncertain concepts. The theorem for embed-

ding PCTL into CTL was proved. The validity, satis-

ﬁability, and model-checking problems of PCTL were

shown to be decidable. The embeddingand decidabil-

ity results indicate that we can reuse the existing CTL-

based algorithms to test the validity, satisﬁability, and

model-checking. Thus, it was shown that PCTL can

be used as an executable logic to represent temporal

reasoning on paraconsistency. We believe that PCTL

can be extensively used for inconsistency-tolerantand

uncertainty reasoning, since N4 and its variants are

known to be very useful for a wide range of applica-

tions such as logic programming and knowledge rep-

resentations (see, e.g., (Odintsov and Wansing, 2003;

Wagner, 1991) and the references therein).

REFERENCES

Almukdad, A. and Nelson, D. (1984). Constructible falsity

and inexact predicates. Journal of Symbolic Logic,

49:231–233.

Beziau, J.-Y. (1999). The future of paraconsistent logic.

Logical Studies, 2:Online.

Chen, D. and Wu, J. (2006). Reasoning about inconsistent

concurrent systems: A non-classical temporal logic.

In Lecture Notes in Computer Science, volume 3831,

pages 207–217.

Clarke, E. and Emerson, E. (1981). Design and synthesis of

synchronization skeletons using branching time tem-

poral logic. In Lecture Notes in Computer Science,

volume 131, pages 52–71.

Clarke, E., Grumberg, O., and Peled, D. (1999). Model

checking. The MIT Press.

da Costa, N., Beziau, J., and Bueno, O. (1995). Aspects of

paraconsistent logic. Bulletin of the IGPL, 3 (4):597–

614.

Easterbrook, S. and Chechik, M. (2001). A framework for

multi-valued reasoning over inconsistent viewpoints.

In Proceedings of the 23rd International Conference

on Software Engineering, pages 411–420.

Gurevich, Y. (1977). Intuitionistic logic with strong nega-

tion. Studia Logica, 36:49–59.

Murata, T., Subrahmanian, V., and Wakayama, T. (1991). A

petri net model for reasoning in the presence of incon-

sistency. IEEE Transactions on Knowledge and Data

Engineering, 3 (3):281–292.

Nelson, D. (1949). Constructible falsity. Journal of Sym-

bolic Logic, 14:16–26.

Odintsov, S. and Wansing, H. (2003). Inconsistency-

tolerant description logic: Motivation and basic sys-

tems. In Trends in Logic: 50 Years of Studia Logica,

pages 301–335.

Priest, G. and Routley, R. (1982). Introduction: paraconsis-

tent logics. Studia Logica, 43:3–16.

Rautenberg, W. (1979). Klassische und nicht-klassische

Aussagenlogik. Vieweg, Braunschweig.

Vorob’ev, N. (1952). A constructive propositional calculus

with strong negation (in russian). Doklady Akademii

Nauk SSR, 85:465–468.

Wagner, G. (1991). Logic programming with strong nega-

tion and inexact predicates. Journal of Logic and

Computation, 1 (6):835–859.

Wansing, H. (1993). The logic of information structures.

In Lecture Notes in Computer Science, volume 681,

pages 1–163.

PARACONSISTENT NEGATION AND CLASSICAL NEGATION IN COMPUTATION TREE LOGIC

469