
DETECTION OF DISCRIMINATING RULES
Fabrizio Angiulli, Fabio Fassetti, Luigi Palopoli and Domenico Trimboli
DEIS, University of Calabria, Italy
Keywords:
Data mining, Rule induction, Exceptional properties.
Abstract:
Assume a population partitioned in two subpopulations, e.g. a set of normal individuals and a set of abnormal
individuals, is given. Assume, moreover, that we look for a characterization of the reasons discriminating one
subpopulation from the other. In this paper, we provide a technique by which such an evidence can be mined,
by introducing the notion of discriminating rule, that is a kind of logical implication which is much more valid
in one of the two subpopulations than in the other one. In order to avoid mining a potentially huge number
of (not necessarily interesting) rule, we define a preference relationship among rules and exploit a suitable
graph encoding in order to single out the most interesting ones, which we call outstanding rules. We provide
an algorithm for detecting the outstanding discriminating rules and present experimental results obtained by
applying the technique in several scenarios.
1 INTRODUCTION
In domains where there is no well assessed knowl-
edge, and given a population partitioned in two sub-
populations, it is of interest to single out the expla-
nations distinguishing the members of one subpopu-
lation from the members of the other subpopulation.
Such a knowledge can be suitably expressed in the
form of rules. Here, we introduce the concept of dis-
criminating rule. Intuitively, a rule is a discriminat-
ing one if it is “much more valid” in one of the two
given subpopulations than in the other one. The dis-
criminating power of a rule is related to the difference
between the confidences it attains over the two sub-
populations under analysis, and can indeed be used to
characterize its quality. In particular, a rule is said to
be discriminating if its discriminating power is above
a user-provided threshold. In this respect, outstand-
ing discriminating rules are pieces of mined knowl-
edge which appear to be promising as building blocks
for the induced domain knowledge to be eventually
reconstructed by the domain expert analyst.
An interesting application scenario thereof con-
cerns the analysis of anomalous subpopulations,
where it is needed to detect the motivations making
some given individuals anomalous. As an example,
assume a population containing genetic information
about both longevous and non-longevoushuman indi-
viduals is given; here, it would be very useful to single
out justifications for the individuals to be longevous
or not. In this respect, this technique can be regarded
as an extension to groups of anomalies of the tech-
nique presented in (Angiulli et al., 2009), where out-
lying properties of a single anomalous individual are
searched for, as accounted for next in this section.
A common problem of any knowledge extractor
system is that the size of mined knowledge might be
so huge to be useless for the analysis purposes. And,
in fact, also the number of discriminating rules can be
very large, whereas only a subset thereof are usually
interesting enough to be promptedto the analyst, inas-
much as most of them will encode redundant knowl-
edge. However, selecting the rules which maximize
the discriminating power value is too a weak criterion
to isolate only interesting ones. Indeed, in most cases,
by augmenting the body of a rule with an arbitrary
simple condition, the discriminating power value as-
sociated with that rule slightly increases due to sta-
tistical fluctuations of the confidence value. To over-
come this problem, we define a novel preference re-
lation notion relating discriminating rules in order to
single out the most interesting ones, also called out-
standing rules. The novelty of this preference relation
is that it is based on a statistical significance test rather
than on generality/specificity criteria.
We point out that, even if a general analogy holds
between the kind of knowledge we consider and sev-
eral pattern discovery tasks, such as those of emerg-
169
Angiulli F., Fassetti F., Palopoli L. and Trimboli D. (2010).
DETECTION OF DISCRIMINATING RULES.
In Proceedings of the 2nd International Conference on Agents and Artificial Intelligence - Artificial Intelligence, pages 169-177
DOI: 10.5220/0002699701690177
Copyright
c
SciTePress

ing patterns, contrasts sets and frequent pattern-based
classification ((Dong and Li, 1999; Zhang et al., 2000;
Bay and Pazzani, 2001; De Raedt and Kramer, 2001;
Cheng et al., 2008), to cite a few), our task consider-
ably differs from the mentioned ones. First, we notice
that, to a closer look, the knowledge mined by the
techniques we are presenting below is actually dif-
ferent. Indeed, emerging patterns, contrast sets and
discriminative patterns can be well represented in the
form of rules, but the only attribute allowed to oc-
cur in their heads is the class attribute, wheras we
search for generic rules with any attribute in their
head, while the class attribute is not considered at
all. Moreover, the interestingness measure charac-
terizing patterns searched for in the cited literature
is based on measuring the frequency gap for the pat-
tern in the two classes, while we use the confidence
gap. While the former measures are (anti-)monotonic
with respect to pattern generality, the latter one is non-
monotonic and, hence, much more challenging to deal
with. Also, these patterns tend to capture knowledge
characterizing the data in a global sense, since they
are based on the notion of absolute frequency. Con-
versely, the knowledge mined by means of discrim-
inating rules characterizes the data in a local sense.
Indeed, the confidence is related to the frequency of
the condition in the head of a rule in the subpopula-
tion of the data selected by its body. Finally, we define
an innovative preference relation based on a statistical
significance test, while most pattern discovery meth-
ods prefer patterns on the basis of generality and/or
measure maximization.
As already noted, the technique presented here
can be regarded as an extension to groups of anoma-
lies of the technique presented in (Angiulli et al.,
2009). Indeed, being the confidence insensitive to ab-
solute frequency, it is more suitable for characterizing
unbalanced subpopulations, as usually occurs when
a group of anomalous individuals is compared to a
whole normal population, than the support. The ma-
jor differences between this work and (Angiulli et al.,
2009) are as follows. In this work two subpopulations
are compared, while in (Angiulli et al., 2009) only a
single (outlier) object can be compared with the over-
all (normal) population; the discriminating measure
adopted there is very different from the one developed
here, since it is designed for a single object, and it is
not at all clear ho to generalize it, if even possible, to
deal with more than a very limited number of anoma-
lous individuals.
The rest of the work is organized as follows. Sec-
tion 2 presents preliminary definitions. Section 3 de-
fines discriminating rule. Section 4 introduces the
notion of outstanding discriminating rule. Section 5
describes the DRUID algorithm for mining outstand-
ing rules. Section 6 presents experimental results. Fi-
nally, Section 7 concludes the work.
2 PRELIMINARIES
In this section some preliminary notions are pre-
sented.
Let A = {a
1
, . . . , a
m
} be a set of attributes and T
a database on A (multi-set of tuples on A). A simple
condition c on A is an expression of the form a = v,
where a ∈ A and v belongs to the domain of a. A
condition C on A is a conjunction c
1
∧ . . . ∧ c
k
of k
(k ≥ 0) simple conditions on A. A condition with
k = 0 is called an empty condition. In the following,
for a conditionC of the form c
1
∧. . .∧c
k
, cond(C) de-
notes the set of simple conditions {c
1
, . . . , c
k
}, while
attr(C) denotes the set {a
i
| (a
i
= v
i
) ∈ C}, that is the
subset of attributes of A appearing in simple condi-
tions c
i
of C.
Let T be a database on a set of attributes A, let t
be a tuple of T. Let c ≡ a = v be a simple condition
on A. The tuple t satisfies c iff t[a] = v, where t[a]
denotes the value the tuple t assumes on a. Let C be
a condition on A. The tuple t satisfies C iff t satis-
fies each simple condition c
i
of C. If C is an empty
condition then each tuple t satisfies C. T
C
denotes the
database including the tuples of T which satisfy C.
Let A = {a
1
, . . . , a
m
} be a set of attributes, a rule
on A is an expression of the form B ⇒ h, where B is
a condition on A and h is a simple condition on A.
B and h are called the body and the head of the rule,
respectively. The size of the rule R ≡ B ⇒ h, denoted
by |R|, is the cardinality of the set cond(B). Let T be
a database on a set of attributes A, let t be a tuple of
T, and let R ≡ B ⇒ h be a rule on A. t satisfies R iff
t satisfies B ∧ h. Let R ≡ B ⇒ h and R
′
≡ B
′
⇒ h
′
be
two rules such that h = h
′
and cond(B) ⊃ cond(B
′
).
Then R is said to be a superrule of R
′
and R
′
is said to
be a subrule of R.
Let T be a database on a set of attributes A, and let
C be a condition on A. The support ofC in T, denoted
by sup
T
(C), is the ratio
|T
C
|
|T|
of the number of tuples
of T satisfying C over the size of T. Given a database
T on A and a threshold σ, 0 ≤ σ ≤ 1, a condition C is
said to be σ-supported by T iff sup
T
(C) ≥ σ.
Let T be a database on a set of attributes A, and
let R be a rule B ⇒ h on A. The confidence of R in T,
denoted by cnf
T
(R), is the ratio
|T
B∧h
|
|T
B
|
of the number
of tuples of T satisfying R over the number of tuples
satisfying B.
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
170
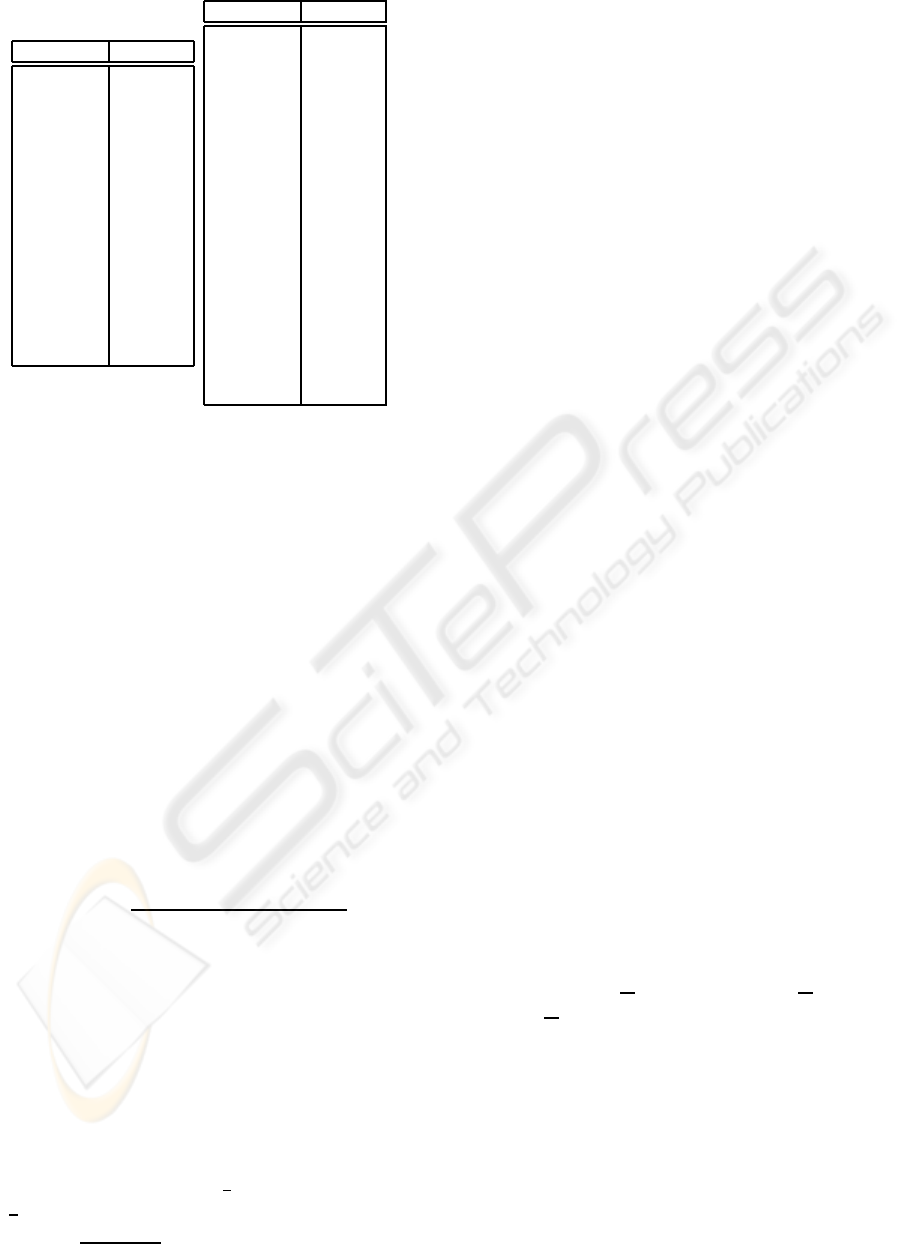
MotherHair ChildHair
brown brown
brown brown
brown brown
brown brown
brown brown
brown blonde
brown blonde
blonde brown
blonde brown
blonde brown
blonde brown
blonde brown
blonde brown
blonde blonde
blonde blonde
(a) T
br
: Brown father
MotherHair ChildHair
brown blonde
brown blonde
brown blonde
brown brown
brown brown
brown brown
brown brown
brown brown
brown brown
brown brown
brown brown
brown brown
brown brown
brown brown
blonde blonde
blonde blonde
blonde blonde
blonde blonde
blonde blonde
(b) T
bl
: Blonde father
Figure 1: Hair color databases.
3 DISCRIMINATING RULES
In this section the notion of discriminating rule is in-
troduced . We will make use of a running example in
order to help illustrating the discussed matter.
Example 1. Figure 1 shows two databases reporting hair
colors of wives and children of some male individuals.
Specifically, the first database, T
br
, is associated with males
with brown hair whereas the second one, T
bl
, is associated
with males with blonde hair. We aim at discovering rules
characterizing only one of the two databases.
We start by providing the definition of discriminating
power. Let T
′
and T
′′
be two databases on a set of
attributes A, and let R be a rule on A. The discrimi-
nating power of R (with respect to T
′
and T
′′
) is:
pow(R) =
|cnf
T
′
(R) − cnf
T
′′
(R)|
max{cnf
T
′
(R), cnf
T
′′
(R)}
.
The discriminating power measures the relative gap
between the confidence value associated with a rule
when we move from a database to the other. Note that,
the larger the absolute difference between cnf
T
′
(R)
and cnf
T
′′
(R), the larger the discriminating power of
R.
Example 1 (continued). Consider Figure 1 again, and the
rule R
ex
:
MotherHair = “blonde” ⇒ ChildHair = “blonde”.
The confidence of r on T
br
is
2
8
= 0.25 whereas on T
bl
is
5
5
= 1, and then the discriminating power of R
ex
is
pow(R
ex
) =
|0.25−1|
max{0.25, 1}
= 0.75. The rule R
ex
asserts that
for a child having a blonde mother, the probability of be-
ing blonde is much higher if its father is blonde rather than
brown. And, in particular, such a probability is 1 in the for-
mer case and 0.25 in the latter case. This knowledge hidden
in the data at hand is clearly expected by the well-known
Mendelian inheritance law. Since brown hair is dominating
over blonde hair, if both parents are blonde haired the child
is blonde. This justifies the value 1 for the confidence of r
on T
bl
. Conversely, if the father is brown and the mother is
blonde, than two cases can arise: the genotype of the father
(i) includes two genes associated with brown hair, or (ii)
includes one gene associated with brown hair and one asso-
ciated with blonde hair. In the case (i) the child is brown for
sure, while in case (ii) the probability of being brown (or,
equivalently, blonde) is about fifty percent. Summarizing,
if (for the sake of simplicity) we assume that cases (i) and
(ii) occur with the same frequency in the considered popu-
lation, than the probability of having a blonde haired child
with a brown father and a blonde mother is about twenty-
five percent, which agrees with the value 0.25 for the confi-
dence of r on T
br
. We also note that R
ex
is more interesting
than the empty-body rule
/
0 ⇒ ChildHair = “blonde”, cor-
responding to the frequency of the value “blonde” on the
attribute “ChildHair” which is approximatively 0.27 on T
br
and 0.42 on T
bl
, resulting in a discriminating power of about
0.37.
The definition of discriminating rule builds on that
of discriminating power.
Let T
′
and T
′′
be two databases on a set of at-
tributes A, let θ
pow
be a threshold (real number in the
range [0, 1]), and let R ≡ B ⇒ h be a rule on A. Then,
R is a discriminating rule iff pow(R) ≥ θ
pow
.
Intuitively, a discriminating rule characterizes suf-
ficiently well the tuples of one database with re-
spect to those of the other. Optionally, we may
require that the rule satisfies some additional con-
straints concerning support and confidence, that are
(c
1
) sup
T
′
(B) ≥ θ
′
sup
, (c
2
) sup
T
′′
(B) ≥ θ
′′
sup
, and (c
3
)
max{cnf
T
′
(R), cnf
T
′′
(R)} ≥ θ
cnf
, where θ
′
sup
, θ
′′
sup
,
and θ
cnf
are suitable thresholds.
Example 1 (continued). For instance, the rule R
ex
is dis-
criminating for θ
′
sup
= θ
′′
sup
= 0.25, θ
cnf
= 0.5, and θ
pow
=
0.7, since sup
T
br
(r) =
8
15
= 0.533, sup
T
bl
(r) =
5
19
= 0.263,
cnf
T
br
(r) =
8
15
= 0.533, and pow(r) = 0.75.
4 OUTSTANDING RULES
As already remarked, while the number of discrimi-
nating rules can be very large, only a subset thereof
can be considered interesting enough to be prompted
to the analyst. Hence, in order to single out the most
interesting rules out of a set of discriminating ones,
DETECTION OF DISCRIMINATING RULES
171

we are next defining a preference relation between
discriminating rules.
4.1 Preference Relation
The preference relation is defined only between pairs
of rules which are one the superrule of the other.
Let T
′
and T
′′
be two databases defined on the
same set of attributes A, let R be a rule on A and let R
′
be a subrule of R. Then, R is preferred to R
′
, denoted
R ≺ R
′
, iff
1. pow(R) > pow(R
′
), and
2. either the difference cnf
T
′
(R) − cnf
T
′
(R
′
) or the
difference cnf
T
′′
(R) − cnf
T
′′
(R
′
) is statistically
significative.
Otherwise, R
′
is preferred to R, and denoted R
′
≺ R.
According to the above definition, a subrule is always
to be preferred to a superrule havinga smaller or equal
discriminating power value. To be preferred, a super-
rule needs not only to have a greater discriminating
power than the subrule, but also a significative gap in
confidence.
The significance of the gap between two confi-
dences can be measured by exploiting a suitable sta-
tistical test. We will describe next in this section the
statistical test employed in the current implementa-
tion of the algorithm.
The rationale underlying this definition is that
shorter rules are generally preferable over longer ones
since longer rules tend to overfit and, also, to be
less intelligible. Moreover, a notion of preference
solely based on the discriminating power is seemingly
far too weak to be practically effective. As already
pointed out, indeed, augmenting the body of a rule
with a randomly selected simple conditions may of-
ten increase the discriminating power associated with
the rule due simply to statistical fluctuations of the
confidence values. Hence, the definition states that a
longer rule is to be preferred only if there is evidence
for at least one of the confidence values associated
with it to be undoubtedly higher.
Note that the relation is not transitive since, for
some three rules r, r
′
andr
′′
, even if both the differ-
ences |cnf(r)−cnf (r
′
)| and |cnf(r
′
)−cnf(r
′′
)| do not
pass the test, it can be the case that the difference
|cnf(r) − cnf(r
′′
)| is indeed large enough to pass the
test.
Significance Test. The statistical significance of
the difference between two confidence values can be
computed by means of the binomial test as described
in the rest of this section.
Let T be a database on A. Let R ≡ B ⇒ h and R
′
≡
B
′
⇒ h be two rules on A such that R is a superrule of
R
′
. Let n
B
be the value |T
B
| and n
R
be the value |T
B∧h
|.
Then, cnf
T
(R) =
n
R
n
B
. Moreover, let n
B
′
be the value
|T
B
′
| and n
R
′
be the value |T
B
′
∧h
|. Then, cnf
T
(R
′
) =
n
R
′
n
B
′
.
Since R is a superrule of R
′
, then the tuples in T
B
are a subset of T
B
′
and, hence, n
B
is smaller than or
equal to n
B
′
. Analogously, the tuples in T
B∧h
are a
subset of T
B
′
∧h
and, hence, n
R
is smaller than or equal
to n
R
′
.
If the attributes belonging to the set
attr(B)\attr(B
′
) were not correlated to the at-
tributes in attr(B
′
), then the tuples in T
B
could be
assumed as generated by a sequence of n
B
random
extractions from T
B
′
. Hence, the random variable X,
representing the number of tuples in T
B
satisfying h,
is distributed according to a binomial distribution,
where a success represents the extraction of a tuple
satisfying h. The number of extractions is n
B
and the
probability of success is the probability of extracting
a tuple satisfying h, which corresponds to
n
R
′
n
B
′
. The
expected value E[X] is the product of the number of
extractions and the probability of success, namely
n
R
= n
B
·
n
R
′
n
B
′
. Hence, the expected confidence of the
rule R is
cnf
T
(R) =
n
B
·
n
R
′
n
B
′
n
B
=
n
R
′
n
B
′
which is equal to the confidence of R
′
.
Clear enough, due to statistical fluctuations, the
number n
R
of tuples satisfying B ∧ h will not be ex-
actly equal to n
R
, and then the value of cnf
T
(R) can
be slightly different from the value of cnf
T
(R
′
).
In order to test if such a difference is due to sta-
tistical fluctuation, it must be checked if it is statisti-
cally significative. To this end the binomial test can
be employed. Let X be a random variable following
the binomial distribution with parameters n = n
B
and
p =
n
R
′
n
B
′
. This test computes the probability to get a
value for the binomial random variable X farther from
n
R
than n
R
, and then checks if this probability is lower
than the significance level 0.05. In other words, it
must be verified if the following inequality holds:
Pr(|X − n
R
| ≥ |n
R
− n
R
|) < 0.05.
Let F (x, y) denote the cumulative binomial distribu-
tion function with parameters x and y. The relation
above can be rewritten as:
F (n
R
+ |n
R
− n
R
|)− F (n
R
− |n
R
− n
R
|) ≥ 0.95. (1)
Clear enough, within the proposed approach, any
other sensible statistical significance test could re-
place the adopted one.
Example 1 (continued). Consider rules R
ex
and R
′
ex
again.
Let us check the significance of the difference between the
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
172

confidence values associated to R
ex
and R
′
ex
on the database
T
bl
. Thus, n
R
ex
= 5, n
B
= 5, n
R
′
ex
= 8 and n
B
′
= 19. n
R
can be computed as 5 ·
8
19
and then n
R
= 2. In order to
evaluate the test the following value has to be determined:
F (2+ |5− 2|) − F (2− |5− 2|). Since the value of the
above expression is 1, hence greater than 0.95, then it can
be concluded that R
ex
is actually preferred to R
′
ex
.
4.2 Outstanding Rules
Here, we define the notion of preferability graph,
which encodes discriminating rules (by means of
nodes) and preferability relations (by means of arcs).
The preferability graph will be exploited to single out
the outstanding discriminating rules.
We have already noted that the number of discrim-
inating rules can be very large, but in general only a
subset thereof can be considered interesting enough
to be prompted to the analyst. In that respect, loosely
speaking, the outstanding discriminating rules will
represent rules whose interestingness for the analyst
is maximal.
Given databases T
′
and T
′′
, and a condition h, a
preferability graph G
h
= (V,U, E) w.r.t. the condition
h (whenever the head condition h is clear by the con-
text, we will omit the superscript of G in referring to
a graph), is a directed graph, with V a set of prefer-
ability nodes (or, simply, nodes – see, below, the defi-
nition of preferability node), U ⊆ V a set of (blocked)
preferability nodes, and E a set of arcs on V.
A preferability node n of a graph G
h
is a node hav-
ing associated a discriminating rule R(n) ≡ B ⇒ h.
Hence, all the rules associated with nodes of a prefer-
ability graph G
h
have the same condition h in their
head. For each discriminating rule of the form B ⇒ h
there exists at most one node in G
h
associated with it.
There exists an arc (n, m) in G
h
from node n to node
m iff R(n) is preferred to R(m).
By
b
G
h
we denote the preferability graph (V,
/
0, E)
where all discriminating rules R ≡ B ⇒ h are repre-
sented.
Given two nodes n and m, m is reachable from n
in G
h
, denoted n → m, iff there exists a directed path
from n to m in G
h
It is assumed that, for each node
n, it holds that n → n. Otherwise, m is not reachable
from n, denoted as n 6→ m. A node n is said to be
a supernode (subnode, resp.) of a node m if R(n) is
a superrule (subrule, resp.) of R(m). Note that by
definition of preferability graph G
h
, for each pairs of
nodes n and m of G
h
such that m is a supernode of
n there exists in G
h
either the arc (n, m) or the arc
(m, n), but not both. A connected component C of
G is a maximal subset of the nodes of G such that,
R
1
: c
1
R
2
: c
1
,c
2
(a)
R
1
: c
1
R
3
: c
1
,c
2
,c
3
R
2
: c
1
,c
2
R
4
: c
1
,c
2
,c
4
(b)
Figure 2: Preferability Graph - Example.
for each n, m ∈ C , n → m hold. Given a node n, the
connected component in G
h
which n belongs to is de-
noted conn(n, G
h
) (or, simply, conn(n) in the follow-
ing).
Given a subset N of V, the restriction G
N
of the
graph G = (V,U,E) on the set of nodes N, is the
subgraph of G induced by the nodes in N, that is
G
N
= (N,U ∩ N,{(n, m) | n, m ∈ N ∧ (n, m) ∈ E}).
Example 2. Consider two databases T
′
and T
′′
. For the sake
of simplicity, assume that all the rules considered in the fol-
lowing score confidence 1 on T
′′
, so that whenever we need
to evaluate the statistical significance of the difference be-
tween two confidences, we restrict our attention on T
′
only.
Suppose that the set R of rules complying with the support
constraints consists in the following two rules:
• R
1
≡ c
1
⇒ h, |T
′
c
1
| = 250, |T
′
c
1
∧h
| = 100;
• R
2
≡ c
1
∧ c
2
⇒ h, |T
′
c
1
∧c
2
| = 250, |T
′
c
1
∧c
2
∧h
| = 100,
where c
1
, c
2
and h are simple conditions.
In order to establish the preference relation between R
1
and R
2
, first their discriminating power has to be computed.
The confidence of R
1
on T
′
is
100
250
= 0.4, whereas it is 1 on
T
′′
. Then, pow(R
1
) = 0.6. Conversely, the confidence of R
2
on T
′
is
50
150
= 0.3, and it is 1 on T
′′
. Then, pow(R
2
) = 0.7.
Since pow(R
1
) < pow(R
2
) and since R
1
is a subrule of R
2
,
we need to evaluate if the gap between the confidences of
R
1
and R
2
is statistically significative in at least one of the
two databases. Because of the gap between the confidences
of R
1
and R
2
on T
′′
is 0, we compute the binomial test only
on T
′
: F (60+ |50− 60|) − F (60− | 50−60|) = 0.9036 <
0.95. Since this gap is not statistically significative, R
1
is
preferred to R
2
. The associated preferability graph is re-
ported in Figure 2(a).
Suppose, now, that R contains two further rules:
• R
3
≡ c
1
∧c
2
∧c
3
⇒ h, |T
′
c
1
∧c
2
∧c
3
| = 45, |T
′
c
1
∧c
2
∧c
3
∧h
| =
9,
• R
4
≡ c
1
∧c
2
∧c
4
⇒ h, |T
′
c
1
∧c
2
∧c
4
| = 45, |T
′′
c
1
∧c
2
∧c
4
∧h
| =
9,
and let us compute the discriminating powers of R
3
and R
4
.
We obtain that pow(R
3
) = 0.8 and pow(R
4
) = 0.8.
First, note that no preferability relation holds for R
3
and R
4
and, then, no arc connects them in the preferability
graph. Note that all the rules have confidence 1 on T
′′
. Con-
sider, now, the pair R
2
and R
3
. Since pow(R
2
) < pow(R
3
)
and R
2
is a subrule of R
3
, we compute the binomial test ob-
taining: F (15+|9− 15|) − F (15− |9− 15|) = 0.9410 <
0.95, asserting that R
2
is preferred to R
3
, and then an arc
DETECTION OF DISCRIMINATING RULES
173

from R
2
to R
3
is there in the preferability graph. Consider
the pair R
1
and R
3
. Since pow(R
1
) < pow(R
3
) but R
1
is
a subrule of R
3
, we compute the binomial test obtaining:
F (18+ |9− 18|) − F (18− |9− 18|) = 0.9942 > 0.95, as-
serting that R
3
is preferred to R
1
, and then an arc from R
3
to
R
1
is there in the preferability graph. This example confirms
that, in general, the preferability relation is not transitive.
As far as R
4
is concerned, its relations with R
1
and R
2
are exactly the same as R
3
. The resulting preferability graph
is reported in Figure 2(b). Observe that R
1
, R
2
, R
3
and R
4
form a connected component.
In order to characterize outstanding discriminat-
ing rules, we next introduce the concept of candidate
rule.
First of all, it is considered the basic situation in
which the graph is a single connected component, and
the notion of candidate node in such a graph is de-
fined. Intuitively, a candidate node is associated with
a potentially outstanding rule.
Let G = (V,U,E) be a preferability graph such
that V is a connected component of G ; a node n in
V is said to be candidate in G iff both the two follow-
ing conditions hold:
1. for each supernode u of n, it holds that
pow(R(n)) ≥ pow(R(u)), and
2. for each subnode u of n, it holds that pow(R(n)) >
pow(R(u)).
The rationale underlying this definition is that, for
each node n in a connected component, there exists an
other node n
′
in the same component such that R(n
′
)
is preferred to R(n), thus from the point of view of the
preference relation, within the same connected com-
ponent, there is no node which is preferable to all
the others. Hence, it is seemingly sensible to single
out as candidates those nodes whose associated rules
score the maximal discriminative power value among
their associated supernodes and subnodes. Moreover,
the equal sign in condition 1 makes it shortest rules
preferable when ties are there in the inclusion hierar-
chy.
Example 2 (continued). Consider the graph of Figure
2(b). This graph forms a connected component. Accord-
ing to the definition provided above, the candidate nodes
are R
3
and R
4
, since their discriminating power is maxi-
mum among those associated with the nodes of the graph
and each of their subrules has strictly smaller discriminat-
ing power. Note that, if the discriminating power of R
1
(or, equivalently, R
2
, resp.) were larger than that of all the
other rules, then the candidate node would only be n
1
(or
n
2
, resp.).
Clear enough, in general, a graph does not include
a single connected component. Thus, we provide next
the definition of source node, which is conducive to
R
1
: c
1
R
3
: c
1
,c
2
,c
3
R
2
: c
1
,c
2
R
4
: c
1
,c
2
,c
3
,c
4
R
5
: c
1
,c
3
,c
4
R
6
: c
3
,c
4
n
1
n
2
n
3
n
4
n
5
n
6
R
7
: c
1
,c
5
n
7
(a)
R
1
: c
1
R
2
: c
1
,c
2
R
5
: c
1
,c
3
,c
4
R
6
: c
3
,c
4
n
1
n
2
n
5
n
6
R
7
: c
1
,c
5
n
7
(b)
Figure 3: Example Graph.
the definition of candidate node in a general prefer-
ability graph.
Let G be a preferability graph; a node n of G is a
source if the following condition holds: for each node
m such that m → n, it holds that n → m.
Hence, a source node is a node that reaches all the
nodes that reach it in turn. Note that there might be
nodes that are reached from a source but not reach the
source.
Example 3. Consider Figure 3a. The node n
2
is a source
since nodes reaching n
2
(namely n
1
and n
3
) are also reached
from it. Conversely, n
6
is not a source since it is reached,
for example, by n
2
but n
6
does not reach n
2
.
Now we are in the position of providing the defi-
nition of candidate node in a general graph.
Let G be a preferability graph. A node n of G is
said to be candidate in G iff n is a source node of G
and n is candidate in G
conn(n)
(according to Def. 4.2
above).
Clear enough, if a node in a connected compo-
nent C is source, then all the nodes in C are sources
as well. Hence, in the graph, there are no nodes out-
side C which are preferable to the nodes in C and,
therefore, the candidate nodes have to be singled out
among those in C .
Example 3 (continued). Consider Figure 3a again. In the
graph the source nodes are n
1
, n
2
and n
3
, all belonging to
the same connected component. Then, the candidate node
is that node amongst n
1
, n
2
and n
3
scoring the highest dis-
criminating power.
Next the definition of transformed graph associ-
ated with a preferability graph G , leading to the defi-
nition of outstanding rule, is given.
Let G = (V,U,E) be a preferability graph. The
transformed graph t(G ) = (V
′
,U
′
, E
′
) associated
with G is the graph obtained as follows:
• V
′
is obtained from V by removing both the can-
didate nodes in G and all their supernodes,
• U
′
is (U ∪S) ∩V
′
, where S is the set containing all
the subnodes of the candidate nodes in G , and
• E
′
is the subset of the arcs in E linking the nodes
in V
′
.
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
174

Since for each G = (V,U, E), with V 6=
/
0, there exists
at least one candidate node in G , the set of nodes of
the graph t(G ) is always a strict subset of V (unless
V =
/
0).
Note that the transformed graph t(G ) is again a
preferability graph, hence the operator t(·) can be ap-
plied also to it. Then, given a non-negative integer
number k ≥ 0, it can be defined the concept of trans-
formed graph of order k associated with G , t
k
(G ),
which is defined recursively as follows: t
0
(G ) is G ,
and, for k > 0, t
k
(G ) is t(t
k−1
(G )).
Let G
/
0
be the preferability graph (
/
0,
/
0,
/
0). We
note that t(G
/
0
) = G
/
0
. Moreover, since t(G ) is a strict
subgraph of G (unless G = G
/
0
), it follows that for
each preferability graph G , there exists a finite inte-
ger number K ≤ |V| such that t
K
(G ) = G
/
0
. Hence,
the operatort(·) always finitely convergesto the graph
G
/
0
.
Now we are in the position of providing the notion
of outstanding node and outstanding rule. A node n is
said to be outstanding in G iff there exists an integer
k ≥ 0 such that the node n is candidate in t
k
(G ) =
(V,U, E) and does not belong to U. A rule R ≡ B ⇒ h
is outstanding iff there exists an outstanding node n in
b
G
h
such that R = R(n).
Example 3 (continued). Consider the graph
b
G
h
shown
in Figure 3(a), then
b
G
h
= ({n
1
, n
2
, n
3
, n
4
, n
5
, n
6
, n
7
},
/
0,
{(n
1
, n
2
), (n
1
, n
4
), (n
1
, n
5
), (n
2
, n
3
), (n
2
, n
4
), (n
3
, n
1
),
(n
3
, n
4
), (n
4
, n
6
), (n
5
, n
4
), (n
6
, n
5
), (n
1
, n
7
)}). Assume that
the discriminating power of R
3
is greater than that of both
R
1
and R
2
. Thus, the only candidate node in
b
G
h
is n
3
, and,
hence, t
1
(
b
G
h
) = (V
′
,U
′
, E
′
) where:
V
′
= {n
1
, n
2
, n
5
, n
6
, n
7
},
U
′
= (
/
0∪ {n
1
, n
2
}) ∩ {n
1
, n
2
, n
5
, n
6
, n
7
} = {n
1
, n
2
}, and
E
′
= {(n
1
, n
2
), (n
1
, n
5
), (n
6
, n
5
), (n
1
, n
7
)}.
The resulting graph is that reported in Figure 3(b). More-
over, n
3
is an outstanding node, since it is a candidate in
t
0
(
b
G
h
) =
b
G
h
and does not belong to U and, as such, R
3
is an outstanding rule. In t
1
(
b
G
h
) there are two source
nodes: n
1
and n
6
which are also candidate nodes. Nev-
ertheless, n
1
is not an outstanding node in t
1
(
b
G
h
) since it
belongs to U
′
, while n
6
is. By applying the t(·) operator
again, we obtain t
2
(
b
G
h
) = (V
′′
,U
′′
, E
′′
) where: V
′′
=
/
0,
U
′′
= {n
1
, n
2
} ∩V
′′
=
/
0, and E
′′
=
/
0. Hence, t
2
(
b
G
h
) = G
/
0
.
Summarizing, in
b
G
h
there are two outstanding nodes,
that are, n
3
and n
6
and, hence, R
3
and R
6
are the outstanding
rules.
Before leaving the section, we provide the ratio-
nale underlying the asymmetry of the operator t(·) in
treating supernodes and subnodes of candidate nodes.
Assume that the supernodes {n
′
} of a candidate
node n are maintained in the transformed graph t(G )
Phase 1:
Determine the set B of conditions co-supported
by the databases T
′
and T
′′
Phase 2:
For each simple condition h that can be built on
the set of attributes A:
a. build the graph
b
G
h
b. Determine the outstanding nodes N in
b
G
h
c. Augment the solution set R with the set of
rules {R(n) | n ∈ N }
Return the rules in R ranked by decreasing dis-
criminating power
Figure 4: The Discriminating RUle InDuctor (DRUID) al-
gorithm.
and marked as blocked, as it is the case for the subn-
odes of n. Thus, if one such a node n
′
becomes can-
didate in t(G ), then all its subnodes n
′′
are marked as
blocked and prevented to be selected as outstanding.
Clearly, while the rule R(n
′
) is not interesting enough
to be prompted to the analyst since its (better) subrule
R(n) has been already selected, this is not the case for
the rule R(n
′′
) which, conversely, is neither a subnode
nor a supernode of R(n).
Assume, conversely, that the subnodes {n
′
} of a
candidate node n are deleted from the transformed
graph t(G ), as it is the case for the supernodes of n.
Moreover, assume that n
′
has a supernode n
′′
in G
such that R(n
′
) is preferred to R(n
′′
). Since the node n
′
is not in t(G ), n
′′
could become an outstanding node.
Recall that the rule R(n
′
) is a subrule of both rules
R(n) and R(n
′′
). Since R(n) is preferred to R(n
′
), it is
the case that the rule R(n) significantly increases the
discriminating power of R(n
′
) by augmenting its body
with some interesting, that is to say correlated, simple
conditions. Furthermore, since R(n
′
) is preferred to
R(n
′′
), it is also the case that the rule R(n
′′
) augments
the body of R(n
′
) with some simple conditions, but
this time they cannot be considered interesting, as the
discriminating power of R(n
′′
) is worse than that of
R(n
′
).
5 ALGORITHM
Given two databases T
′
and T
′′
on the same set of
attributes A, we are interested in finding the outstand-
ing rules discriminating T
′
from T
′′
. In this section
we present the algorithm DRUID (for Discriminating
RUle InDuctor) solving this task. The algorithm con-
sists in two main phases (see Figure 4).
We say that a condition is co-supported by
databases T
′
and T
′′
if its support on database T
′
is
DETECTION OF DISCRIMINATING RULES
175
above threshold θ
′
sup
and its support on database T
′′
is above threshold θ
′′
sup
. First of all the set B of co-
supported conditions in the two databases has to be
determined (phase 1). This can be done by adapt-
ing any efficient frequent itemset mining algorithm
to work simultaneously on two databases in order to
take into account only co-supported conditions. In
our current implementation an A-priori like algorithm
(Rakesh et al., 1993) is employed to compute the set
B of co-supported conditions. The set B is mined
only once, since it can be “reused” for each potential
head.
During Phase 2 the outstanding discriminating
rules are mined. For each simple condition h employ-
able as head of a discriminating rule, phase 2a of the
algorithm builds the graph
b
G
h
associated with h. Sub-
sequent phase 2b determines the outstanding nodes in
b
G
h
by applying the operator t(·), until the graph be-
comes empty. The outstanding nodes in the graphs
b
G
h
are collected into the set R , and the associated
outstanding rules are eventually presented to the user.
As for the temporal cost of the method, the cost
of Phase 1, corresponding to the execution of the A-
priori algorithm, is in general exponential with re-
spect to the number of database attributes. As for the
cost of Phase 2, it is polynomial in the size of the
graph, whose number of nodes is upper bounded by
the size |B | of the output of the A-priori algorithm,
and linear in the number of tuples of the database, due
to the need of computing the confidence of the rules.
6 EXPERIMENTAL RESULTS
In this section, we present experimental results ob-
tained by applying the proposed technique on some
real databases. We considered two extensively used
test datasets, that are Mushroom
1
and Census
2
(also
referred to in the following as DS1 and DS2, respec-
tively). The Mushroom dataset includes descriptions
of 8,124 hypothetical samples corresponding to 23
species of gilled mushrooms in the Agaricus and Lep-
iota Family. There are 22 categorical attributes. Each
species is identified as edible (4,208 instances) or poi-
sonous (3,916 instances). On the basis of this clas-
sification, the data was partitioned in two databases
T
e
and T
p
. The Census dataset contains information
about old people. It consists of 333,011 tuples each
of which is composed of 10 categorical attributes plus
one class attribute Income, which represents the an-
1
http://archive.ics.uci.edu/ml/.
2
http://www.cs.waikato.ac.nz/ml/weka/
index datasets.html.
0 0.2 0.4 0.6 0.8 1
0
2
4
6
8
10
12
14
x 10
4
Support
Number of discriminating rules
θ
cnf
= 0.0
θ
cnf
= 0.5
θ
cnf
= 0.9
(a) DS1: discriminating rules
0 0.2 0.4 0.6 0.8 1
0
1000
2000
3000
4000
5000
6000
Support
Number of discriminating rules
θ
cnf
= 0.0
θ
cnf
= 0.5
θ
cnf
= 0.9
(b) DS2: discriminating rules
0 0.2 0.4 0.6 0.8 1
0
500
1000
1500
2000
2500
Support
Number of outstanding rules
θ
cnf
= 0.0
θ
cnf
= 0.5
θ
cnf
= 0.9
(c) DS1: outstanding rules
0 0.2 0.4 0.6 0.8 1
0
50
100
150
200
250
300
350
Support
Number of oustanding rules
θ
cnf
=0.0
θ
cnf
=0.5
θ
cnf
=0.9
(d) DS2: outstanding rules
0.1 0.2 0.3 0.4 0.5 0.7 1
10
−2
10
−1
10
0
10
1
10
2
10
3
10
4
Support
Execution time of second phase [sec]
θ
cnf
= 0.0
θ
cnf
= 0.5
θ
cnf
= 0.9
(e) DS1: execution time
0.1 0.2 0.3 0.4 0.5 0.7 1
10
−2
10
−1
10
0
10
1
10
2
Support
Execution time of phase 2 [sec]
θ
cnf
= 0.0
θ
cnf
= 0.5
θ
cnf
= 0.9
(f) DS2: execution time
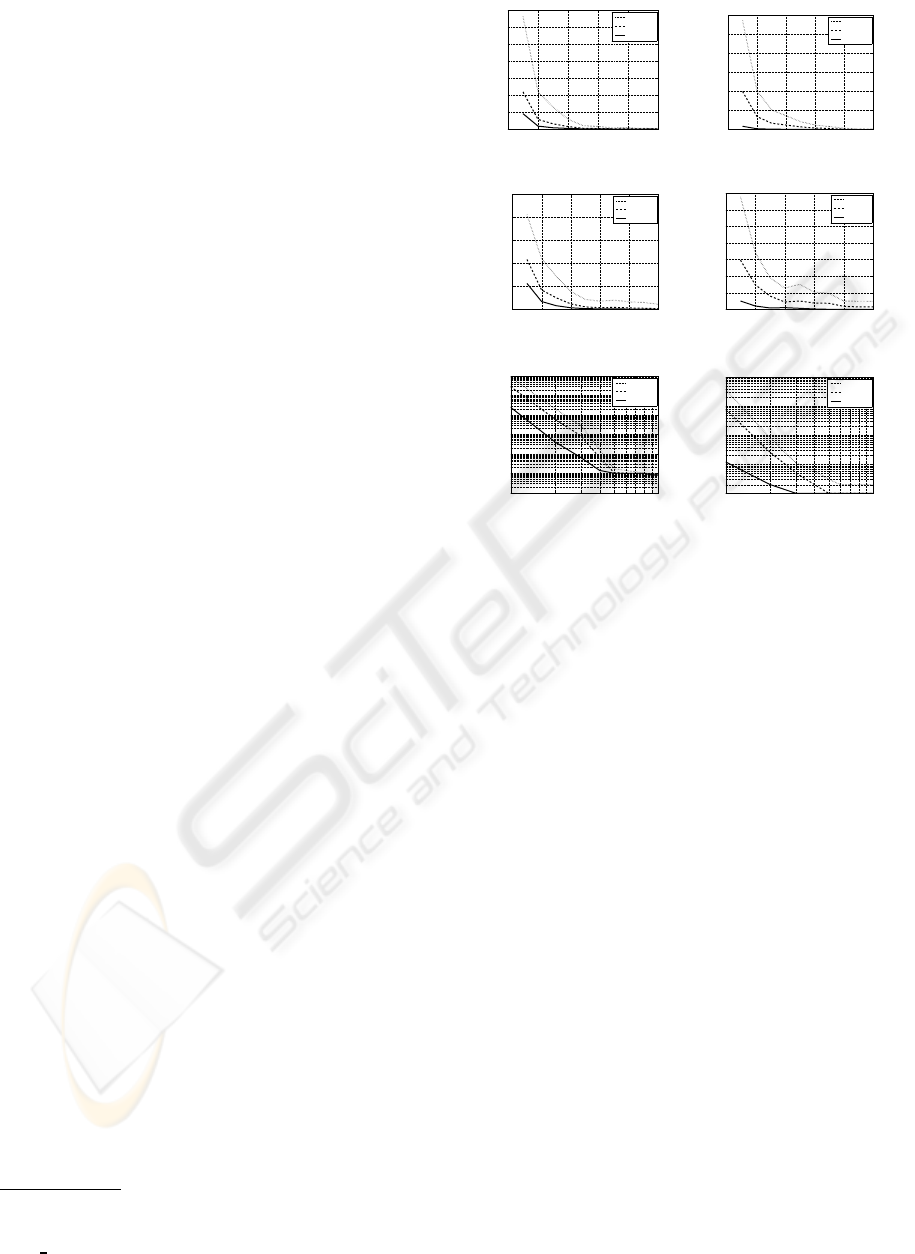
Figure 5: Experimental results.
nual income, assuming two distinct values, that are
“below50K” and “over50K”. Hence, we split it in
two databases, T
<50
(consisting of 327,216 tuples)
and T
>50
(consisting of 5,795 tuples), on the basis
of the value of the class attribute. We considered
this dataset in order to verify the technique on two
significantly unbalanced subpopulations. Indeed, the
T
>50
subpopulation can be considered here as includ-
ing “anomalous” individuals to be compared against
the ”normal” subpopulation T
<50
.
Experiments are organized as follows. First of
all, we present a sensitivity analysis of the method
by measuring execution time, number of discriminat-
ing rules, and number of outstanding rules, for vari-
ous combinations of the threshold parameters θ
sup
and
θ
cnf
. Following that, we shall comment upon some
outstanding rules.
Figure 5 reports the results of the sensitivity anal-
ysis. The parameter θ
sup
was varied between 0.1 and
1.0, while three distinct values for the parameter θ
cnf
were considered: 0.0, 0.5, and 0.9. Figures 5(a) and
5(b) report the number of discriminating rules. Fig-
ures 5(c) and 5(d) report the number of outstanding
rules. Finally, Figures 5(e) and 5(f) report the execu-
tion time (in seconds). The time required by Phase 2
clearly depends on the number of discriminating rules
in the databases. This number increases sensibly only
for low support values, but in all cases the DRUID al-
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
176

gorithm terminated its work in a reasonable amount
of time. It employed about three hours on the hardest
instance considered on Census. We point out that this
execution time was reached for very low values of the
thresholds and, in particular, for θ
cnf
= 0. Indeed, for
more sensible values of the parameters it rapidly de-
creases to few seconds. Finally, the following table
shows the execution times (in seconds) of the Phase
1 of the algorithm, that is the variant of the A-priori
algorithm for mining co-supported conditions.
θ
sup
= 0.1 0.2 0.3 0.5 0.7 0.9 1.0
Mushroom 0.41 0.24 0.16 0.05 0.03 0.01 0.01
Census 4.30 2.55 2.19 1.28 0.54 0.01 0.01
Next we comment upon some oustanding rules re-
turned by running DRUID. Consider the Mushroom
dataset. The rule cap−sur face = f ∧ cap−shape =
x ⇒ odor = n, has pow = 0.99, cnf
e
= 0.97, cnf
p
=
0.01, sup
e
= 0.17, sup
p
= 0.11. It concerns mush-
rooms with fibrous cap surface and convex cap shape.
The rule asserts that edible mushrooms thereof are
very likely to be odorless, while poisonous are very
likely to be odorous.
The rule cap−color = g ∧ gill−spacing = c ⇒
ring−type = p, has pow = 0.84, cnf
e
= 1.00, cnf
p
=
0.16, sup
e
= 0.15, sup
p
= 0.20. It concerns mush-
rooms with gray cap color and closed gills. The
rule asserts that edible mushrooms thereof are more
likely to have a pendant ring than poisonous ones.
The rule stalk−surface−b−r = s∧ ring−number =
o ⇒ gill−size = n, has pow = 0.92, cnf
e
= 0.07,
cnf
p
= 0.90, sup
e
= 0.72, sup
p
= 0.37. It concerns
mushrooms with smooth surface of the stalk under
the ring and one ring. The rule asserts that poisonous
mushrooms thereof are more likely to have narrow
gills than edible ones.
Consider now the Census dataset. The rule
immigr = be fore75 ⇒ english = poor, has pow =
0.83, cnf
T
<50
= 0.42, cnf
T
>50
= 0.07, sup
T
<50
= 0.10,
sup
T
>50
= 0.12. It concerns people immigrated be-
fore year 1975. The rule asserts that the individ-
uals thereof whose income is below 50K are more
likely to speak a poor English than those having in-
come above 50K. The rule urban = false ⇒ race =
black, has pow(R
2
) = 0.80, cnf
T
<50
= 0.42, cnf
T
>50
=
0.09, sup
T
<50
= 0.23, sup
T
>50
= 0.15. It concerns
people living in rural areas. The rule asserts that
the individuals thereof whose income is below 50K
are more likely to be black than those having in-
come above 50K. The rule region = midw ∧ age =
below75 ⇒ sex = male, has pow = 0.80, cnf
T
<50
=
0.27, cnf
T
>50
= 0.55, sup
T
<50
= 0.11, sup
T
>50
= 0.12.
It concerns people whose age is below 75 years and
living in the Midwest. The rule asserts that the indi-
viduals thereof whose income is above 50K are more
likely to be male than those having income below
above 50K.
7 CONCLUSIONS
In this paper, the problem of characterizing the fea-
tures distinguishing two given populations has been
analyzed. We introduced the notion of discriminating
rule, a kind of logical implication which is much more
valid in a population than in the other one. We sug-
gested their use for characterizing anomalous subpop-
ulations. In order to avoid for the analyst to be over-
whelmed by the potentially huge number of rules dis-
criminating the two populations, we defined an orig-
inal notion of preference relation among discriminat-
ing rules, which is interesting from a semantical view-
point, but it is challenging to deal with since it is
not transitive and, hence, no monotonicity property
can be exploited to efficiently guide the search. We
proposed the DRUID algorithm for detecting the out-
standing discriminating rules, and discussed prelimi-
nary experimental results.
REFERENCES
Angiulli, F., Fassetti, F., and Palopoli, L. (2009). Detect-
ing outlying properties of exceptional objects. ACM
Trans. on Database Systems (TODS), 34(1).
Bay, S. D. and Pazzani, M. J. (2001). Detecting group
differences: Mining contrast sets. Data Mining and
Knowledge Discovery, 5(3):213–246.
Cheng, H., Yan, X., Han, J., and Yu, P. S. (2008). Direct dis-
criminative pattern mining for effective classification.
In ICDE, pages 169–178.
De Raedt, L. and Kramer, S. (2001). The levelwise ver-
sion space algorithm and its application to molecular
fragment finding. In IJCAI, pages 853–862.
Dong, G. and Li, J. (1999). Efficient mining of emerging
patterns: Discovering trends and differences. In KDD,
pages 43–52.
Rakesh, A., Tomasz, I., and Arun, S. (1993). Mining asso-
ciation rules between sets of items in large databases.
In SIGMOD, pages 207–216.
Zhang, X., Dong, G., and Ramamohanarao, K. (2000). Ex-
ploring constraints to efficiently mine emerging pat-
terns from large high-dimensional datasets. In KDD,
pages 310–314.
DETECTION OF DISCRIMINATING RULES
177
