TOWARDS A COMPREHENSIVE TEAMWORK MODEL FOR

HIGHLY DYNAMIC DOMAINS

Hendrik Skubch, Michael Wagner, Roland Reichle, Stefan Triller and Kurt Geihs

Distributed Systems Group, Kassel University, Wilhelmsh

oher Allee 73, Kassel, Germany

Keywords:

Mutli-agent systems, Teamwork, Coordination, Coorperation, Dynamic domains.

Abstract:

Cooperative behaviour of agents within highly dynamic and nondeterministic domains is an active ﬁeld of

research. In particular establishing responsive teamwork, where agents are able to react to dynamic changes in

the environment while facing unreliable communication and sensory noise, is an open problem. Unexpectedly

changing situations force agents to react and adapt under tight time-constraints. Hence they often cannot

communicate or agree upon their decisions before acting upon them. We present a novel model for cooperative

behaviour geared towards such domains. In our approach, the agents estimate each other’s decision and

correct these estimations once they receive contradictory information. We aim at a comprehensive approach for

agent teamwork featuring intuitive modelling capabilities for multi-agent activities, abstractions over activities

and agents, and clear operational semantics for the new model. We show experimentally that the resulting

behaviour stabilises towards teamwork and can achieve a cooperative goal.

1 INTRODUCTION

Highly dynamic and nondeterministic domains im-

pose a number of challenges for the realisation of

responsive yet coherent teamwork of autonomous

agents. Teams of agents operating in such domains

have to be robust against sensory noise, breakdown

of individual agents, and unexpectedly changing situ-

ations. Such changes in the environment require the

agents to react and adapt under tight time-constraints.

This entails that it is often impossible to explicitly

communicate – or even agree upon – a decision be-

fore acting on it. Maintaining a highly responsive and

coherent teamwork is even more difﬁcult, if commu-

nication is unreliable.

In this paper, we introduce a novel approach for

cooperative behaviour, focusing on teams of agents

acting in highly dynamic domains. The model con-

sists of the agent oriented language ALICA (A Lan-

guage for Interactive Cooperative Agents), which pro-

vides modelling facilities for cooperative behaviour,

and clear operational semantics, that determine in de-

tail how agents act.

ALICA is closely related to STEAM (Tambe,

1997), a model for teamwork based on both Joint

Intentions (Levesque et al., 1990) and Shared

Plans (Grosz and Kraus, 1996). In contrast to

STEAM, ALICA agents in general do not establish

joint intentions before acting towards a cooperative

goal. Instead, each agent estimates the decisions of

its teammates and acts upon this prediction. The re-

sulting internal states are communicated periodically,

thus allowing for individual decisions to be corrected

dynamically. ALICA provides language elements to

enforce an explicit agreement, resulting in a joint in-

tention, for activities that require time critical syn-

chronisations, such as lifting an object cooperatively.

We present operational semantics for ALICA pro-

grams based on 3APL’s semantics (Hindriks et al.,

1999). ALICA programs are modelled from a global

perspective, such that team activities are described di-

rectly instead of being the result of interacting single

agent programs. The operational semantics explic-

itly dictates how to execute an ALICA program. The

complete semantics does not ﬁt in the scope of this

paper, but can be referred to in (Skubch et al., 2009).

ALICA features a two-layered abstraction be-

tween concrete activities and agents. Roles abstract

over agents, describing capabilities and resulting pref-

erences for speciﬁc tasks. Tasks, on the other hand,

abstract from speciﬁc activities, and relate similar ac-

tivities within different contexts, called plans. This

allows for plans to be speciﬁed independently of the

team executing them and teams to be speciﬁed inde-

pendently of the plans they might execute.

The state of the art is enhanced by providing a

121

Skubch H., Wagner M., Reichle R., Triller S. and Geihs K. (2010).

TOWARDS A COMPREHENSIVE TEAMWORK MODEL FOR HIGHLY DYNAMIC DOMAINS.

In Proceedings of the 2nd International Conference on Agents and Artiﬁcial Intelligence - Agents, pages 121-127

DOI: 10.5220/0002701201210127

 SciTePress

rich language to specify cooperative behaviour, a pro-

gramming model with clear operational semantics,

and elaborate coordination mechanisms for respon-

sive teamwork at the same time. Thus, our approach

can be considered as a step towards a comprehensive

team-work model for highly dynamic domains.

The next section discusses related work and de-

scribes ALICA’s relation to STEAM and 3APL in

more detail. Section 3 formally introduces the lan-

guage, whose semantics is discussed in Section 4. In

Section 5, we present evaluation results within the

robotic soccer domain. Finally, Section 6 concludes

the paper and hints at future work.

2 RELATED WORK

Many research activities tackled the problem of de-

scribing agent behaviour and addressed the chal-

lenge to establish coherent teamwork of autonomous

agents. As a result there exist several teamwork

theories. One of them is the Joint Intentions The-

ory (Levesque et al., 1990), founded on BDI (Brat-

man, 1987). The framework focuses on a team’s joint

mental state, called a ’joint intention’. A team jointly

intends a team action if team members jointly commit

to an action while in a speciﬁed mental state. In or-

der to enter a joint commitment, team members have

to establish appropriate mutual beliefs and individual

commitments. Although the Joint Intentions Theory

does not mandate communication and several tech-

niques are available to establish mutual beliefs about

actions from observations, communication currently

seems to be the only feasible way to attain joint com-

mitments. However, a single joint intention for a

high-level goal seems not appropriate to model team

behaviour in detail and to ensure coherent teamwork.

The Shared Plans Theory (Grosz and Kraus, 1996;

Grosz and Sidner, 1990) helps to overcome this short-

coming. In contrast to joint intentions, the Shared

Plans Theory is not based on a joint mental attitude

but on an intentional attitude called ’intending that’.

’Intention that’ is deﬁned by a set of axioms that guide

an individual to take actions, enabling or facilitating

its teammates to perform assigned tasks. A Shared-

Plan for group action speciﬁes beliefs about how to

do an action and sub actions.

STEAM (Tambe, 1997) builds on both teamwork

theories and tries to combine their beneﬁts. It starts

with joint intentions, but then builds up hierarchi-

cal structures that parallel the Shared Plan Theory.

So STEAM formalises commitments by building and

maintaining joint intentions and uses Shared Plans to

treat a team’s attitudes in complex tasks, as well as

unreconciled tasks.

In contrast to STEAM, ALICA agents do not es-

tablish joint intentions before acting towards a coop-

erative goal. Instead, each agent estimates the de-

cisions of its team mates and acts upon this predic-

tion. Conﬂicting individual decisions are detected

and corrected using periodically communicated inter-

nal states of teammates. Although STEAM provides

approaches for selective communication and track-

ing of mental attitudes of teammates, we argue that

for highly dynamic domains and time-critical applica-

tions the strict requirement to establish or estimate a

joint commitment before a joint activity is started has

to be skipped. We deem agents that decide and act un-

til contradictory information is available to be much

more suitable for such applications. The assignment

of agents to teams and teams to operators employed

by STEAM seems to be too static for highly dynamic

domains. In a soccer game, for example, a defend-

ing robot should also be able to carry out an attack

if it obtains the ball and the game situation seems to

be promising to do so. In order to facilitate such be-

haviour, we provide a different deﬁnition of roles and

incorporate the concept of tasks. With its coordina-

tion approach, ALICA also abandons the concept of

a ’team-leader’ which STEAM assumes for different

purposes in team coordination.

All previously described teamwork models have

in common that they provide mechanisms to rea-

son about or to establish teamwork, but they do not

specify the internals of plans or operators. STEAM,

and its implementation TEAMCORE (Pynadath et al.,

1999), just assume reactive or situated plans, but do

not specify the internal control cycle of an agent.

Here, agent programming languages inspired the de-

sign of ALICA, in particular 3APL. ALICA incorpo-

rates many concepts of 3APL, e.g., the deﬁnition of

the belief base, substitution of variables and the inter-

pretation of goals as ’goals-to-do’, which are not de-

scribed declaratively but via plans that are directed to-

wards achieving a goal. Furthermore, ALICA deﬁnes

its operational semantics similar to 3APL through a

transition system. However, in contrast to ALICA,

3APL also facilitates explicit speciﬁcation of goals.

It introduces rule sets and beliefs to allow reasoning

about both, goals and plans. 3APL understands itself

as an abstract language, allowing to specify the de-

liberative cycle itself. ALICA is speciﬁcally aimed at

modelling multi-agent strategy from a global perspec-

tive. This is impossible in 3APL. Moreover, ALICA’s

transitional rule system is geared towards cooperative

agents, and hence is much more speciﬁc then the rule

system employed by 3APL.

Considering the aspects above, we argue that AL-

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

122

ICA enhances the state of the art in team-work mod-

els, as it provides a further step towards a compre-

hensive approach that provides support for all aspects

of team coordination and also for explicit program-

ming of team behaviour from a global perspective at

the same time. With its approach to allow agents to

decide and act towards a certain team-goal without

explicit establishment of a joint commitment, it is also

very suitable for highly dynamic domains that require

fast decisions and actions and do not allow explicit

communication and negotiations beforehand.

3 THE LANGUAGE

The central notion within ALICA are plans. A plan

describes speciﬁc activities, a team of agents has to

execute in order to achieve a certain goal. Plans

are modelled similar to petri-nets, containing states

and transitions between the states. Each transition is

guarded by a condition, which must be believed to

hold by an agent in order to progress along it.

The set of all plans in an ALICA program is de-

noted by P . Z denotes all states. The belief base of

each agent is described in a logic with language L,

hence all conditions are elements of L. Each transi-

tion τ is an element of Z × Z ×L.

ALICA abstracts two-fold from agents, by tasks

and roles. A role is assigned to an agent based on

its capabilities. This assignment is treated to be com-

partively static, i.e., it holds until the team compo-

sition changes. This is the case if an agent joins or

leaves the team, e.g., due to being incapacitated.

Tasks on the other hand abstract from speciﬁc

paths within plans. As such, they denote similar ac-

tivities in different plans. If a group of agents is

to execute a plan, the corresponding tasks are allo-

cated to the available agents based on the situation at

hand and the roles the agents are assigned. This two-

layered abstraction allows for programs to be speci-

ﬁed independently of the team composition that will

be on hand during execution. A team composition

can be described solely by the roles each agent is as-

signed, while plans can be described without referring

to roles. Each role has a numeric preference towards

tasks, which allows roles to be mapped onto tasks dy-

namically during runtime (see Section 4.1).

Since plans describe activities for multiple agents,

they have multiple initial states, each of which is an-

notated by a task. Hence, a task abstracts from spe-

ciﬁc activities within plans, and multiple plans can be

annotated with the same tasks. For instance, a plan to

build a tower and one to build a bridge might both

contain the task of moving building blocks. Since

tasks might require multiple agents, each task-plan

pair (p, τ) is annotated by a cardinality, i.e., by an in-

terval over N

∪{∞}, denoting how many agents must

at least and may at most be allocated to τ in p.

The applicability of a plan in a situation is mea-

sured in two ways. Firstly, each plan p is annotated

by a precondition Pre(p), which has to hold when

the agents start to execute it, and a runtime condition

Run(p), which has to hold throughout its execution.

Secondly, each plan p is annotated by a utility func-

tion U

, which is used to evaluate the plan together

with a potential allocation of agents to tasks within p

wrt. a situation. A utility function maps believed or

potential situations onto the real numbers. Both con-

ditions and utility functions solely refer to the belief

base of an agent, which contains believed allocations.

Plans can be grouped together in plan types, pro-

viding the agents with sets of alternatives for solv-

ing a particular problem. Choosing a speciﬁc plan

from a plan type is done autonomously by the agents

in question. This selection is guided by the utility

functions and conditions of the plans involved. Each

state contains an arbitrary number of plan types. For

each plan type, the agents involved have to choose

a plan and execute it, i.e., multiple plans, one from

each plan type, are executed in parallel. Additionally,

each state contains an arbitrary number of behaviours.

Behaviours are atomic single-agent action programs.

The set of all behaviours is denoted by B. Each be-

haviour within a state is meant to be executed by all

agents inhabiting the corresponding state.

The relationship between states, plans and plan

types spans a hierarchical structure, called the plan

tree of an ALICA program.

4 SEMANTICS

The semantics of ALICA is given by a transitional

rule system, which describes how the internal states

of agents change over time. These internal states are

referred to as agent conﬁgurations. Additionally, a set

of axioms, Σ

, constrains these conﬁgurations.

Deﬁnition 4.1 (Agent Conﬁguration). An agent con-

ﬁguration is a tuple (B, ϒ, E, θ, R), where B is the

agent’s belief base, ϒ its plan base, E ⊆ B × Z the

set of behaviours b the agent executes together with

the state in which b occurs, θ a substitution, and R is

a set of roles assigned to the agent.

The plan base contains triples (p, τ, z), indicating

that the agent is committed to task τ in plan p and cur-

rently inhabits state z within p. Each triple is reﬂected

by a literal in the belief base, In(a, p, τ, z), represent-

ing the belief that (p, τ, z) is an element of agent a’s

TOWARDS A COMPREHENSIVE TEAMWORK MODEL FOR HIGHLY DYNAMIC DOMAINS

123

plan base. Similarly, HasRole(a,r) captures the belief

that role r is assigned to a.

4.1 Task Allocation and Plan Selection

Whenever an agent enters a state, it has to take care

that a plan out of each plan type within that state is ex-

ecuted. This does not entail that the agent is required

to execute the plan, it is sufﬁcient to come to the con-

clusion that there are agents executing it. This gives

rise to the allocation problem.

An allocation done by agent a for a plan p is a

set of literals of the form In(a

, p, τ, z), referred to as

TAlloc(a, p|F ). The allocation is calculated under

the set of assumptions F . Normally, it equals the be-

lief base of a. In case of planning, F can refer to

a potential situation in the future. A task allocation is

subject to several constraints, such as the pre- and run-

time conditions of plan p, Pre(p) and Run(p). More-

over, it must be consistent with the assumptions F

under which it is computed, and the axioms Σ

. E.g.,

rule out agents taking on multiple tasks within the

same plan. Deﬁnition 4.2 captures these constraints.

Deﬁnition 4.2 (Valid Task Allocation). A Task Allo-

cation TAlloc(a, p|F ) for agent a with the conﬁgura-

tion (B, ϒ, E, θ, R) is valid iff

• Σ

∪F ∪ TAlloc(a, p|F ) 6|= ⊥

• Σ

∪F ∪ TAlloc(a, p|F ) |= (Pre(p) ∧ Run(p))θ

• Σ

∪F ∪ TAlloc(a, p|F ) |= TeamIn(p)

where TeamIn(p) denotes that the given team of

agents A executes plan p. Formally:

TeamIn(p)

de f

= (∀τ ∈ Tasks(p))(∃n

, n

)

ξ(p, τ) = (n

, n

) ∧

(∃A

⊆ A ∧ n

≤ |A

| ≤ n

∧

(∀a

∈ A )a

∈ A

↔ (∃z) In(a

, p, τ, z)

where ξ(p, τ) refers to the cardinalities of task τ in

plan p.

The set of agents that can be referred to in an al-

location is limited by Σ

to the ones believed to be

in the respective parent state z, i.e., for each agent a

occuring in TAlloc(a, p|F ), In(a

, p

, τ

, z) must hold

in F . Among all valid task allocations for p, agent a

has to choose the one that maximises the utility func-

tion of plan p. Various algorithms can be used for

this maximisation problem; we use A

∗

in our imple-

mentation. Since p is an element of a plantype P,

the optimisation extends to all plans in P. In other

words, there must not be a plan p

in P for which

a valid task allocation T

wrt. F exists such that

(F ∪ TAlloc(a, p|F )) < U

(F ∪ T

). This prob-

lem can trivially be integrated into the maximisation

by extending the search space to all elements of P.

Figure 1: Recursive Task Allocation.

If the task allocation of agent a allocates a to task

τ in p, a enters a state identiﬁed by p and τ, denoted

as Init(p, τ). Intuitively, this is the initial state for task

τ in plan p. Since Init(p, τ) can contain plan types

again, new allocation problems arise. For every plan

type P

in Init(p, τ), a plan p

in P

has to be chosen,

such that TAlloc(a, p

|F ∪ TAlloc(a, p|F )) is valid.

So, the task allocation is recursive. This recursion is

be captured by a backtracking algorithm, backtrack-

ing whenever a valid allocation cannot be found.

Note, the recursion applies only to those states the

calculating agent enters. As such, agents only deal

with a local view of the complete allocation. Figure 1

depicts an example of the backtrack search and this

local view, where agent a allocates agents a, b, and c.

Figure 1(a) shows agent a’s result of the recursive task

allocation. Agent a has to allocate itself within p

If it cannot ﬁnd a valid task allocation for p

, back-

tracking occurs (see Figure 1(b)). Figure 1(c) shows

the ﬁnal task allocation, where agent a has swapped

places with agent c within plan p

. Note, that a has

not allocated b and c within p

. This reﬂects the local

view of a on this plan tree.

After an allocation is computed, the belief base is

updated accordingly and the agent acts based on the

calculated assumptions. In order to deal with poten-

tial inconsistencies, each agent communicates its plan

base periodically. Whenever an agent receives a mes-

sage, its belief base is updated. Conﬂicts can be de-

tected and are dealt with by speciﬁc transitional rules.

They entail a reallocation, an abortion of the plan, or

the pursuit of an alternative course of action. Here,

we focus on reallocation, which an agent performs if

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

124

it believes this will improve the corresponding utility

function. In particular, the utility of a plan with an in-

valid allocation is deﬁned to be 0, and greater or equal

0 in case of a valid one.

4.2 Transitional Rule System

Transition rules deﬁne how an agent’s conﬁguration

changes during a single deliberation cycle wrt. the ex-

ecuted ALICA program. Thus, they describe the op-

erational semantics of ALICA. Each rule is guarded

by a condition and transforms the current conﬁgura-

tion of an agent into a new one.

The complete rule system (Skubch et al., 2009) is

out of scope of this paper. Essentially, each rule gov-

erns a reaction to speciﬁc situations an agent faces

with respect to an ALICA program. Rules are parti-

tioned into two sets. First, so-called operational rules,

describing the normal operation of a program. Sec-

ond, repair rules, which handle unexpected failures.

The operational rules deﬁne how an agent exe-

cutes an ALICA program. They monitor transitions,

describe how an agent leaves a state, and enforce task

allocations for newly entered states. Furthermore, op-

erational rules react to successful execution of be-

haviours or plans and propagate this information up

the plan tree. A precedence order over rules is used to

break ties between multiple applicable rules.

Repair rules handle the cases where something

went wrong. Depending on the kind of failure, the

corresponding behaviour or plan is ﬁrst aborted, and

afterwards either retried, replaced by an alternative or,

if both is impossible, the failure is propagated up the

plan tree. Each of these reactions is handled by a par-

ticular rule. In case two repair rules can be applied,

precedence is given to the one that requires the small-

est change. For example, retrying a particular plan is

less of an effort than propagating the failure upwards.

Repair rules are always overruled by operational

rules. Thereby, unnecessary repairs are avoided, and

domain speciﬁc failure handling can be modelled by

declaring transitions referring to believed failures.

The transitional rule system is not only used to

update agent conﬁgurations, but it allows the agents

to track each other’s internal state. For instance, if

an agent follows a transition, it will assume that all

other agents in the corresponding state do the same.

This assumption is corrected once an agent receives a

message containing the plan base of another.

A speciﬁc repair rule is used to handle cases where

the utility of a plan in execution is believed to be com-

paratively low. In this case, the current utility of the

plan is compared with the potential best utility achiev-

able by reallocating all involved agents. We present

this rule in more detail as it is of major importance

to the evaluation in Section 5. Given the utility func-

tion U

of the plan in question, the belief base B of

the agent containing the allocation T of p, the agent

adopts a new allocation T

= TAlloc(a, p|B \ T ) if

((B \ T ) ∪ T

) − U

(B) − Di f (p, T, T

) > t

holds, where t

is a plan speciﬁc threshold and Di f is

a similarity measurement over allocations.

Di f (p, T, T

) =

1 −

|{a|In(a, p, τ, z) ∈ T ∧ (∃z

)In(a, p, τ, z

) ∈ T

Both the threshold and the similarity measurement are

used to stabilise an assignment once it is adopted.

5 EVALUATION

We integrated ALICA into a software framework for

autonomous robots and use it to control a robotic team

in the RoboCup Midsize league. The execution loop

of each robot has a frequency of 30Hz. Each cycle,

a robot has to process new sensory data and incom-

ing messages, update its belief base, check and ap-

ply transitional rules, and execute behaviours. Every

robot peridiocally broadcasts its plan base and parts of

its belief base, more speciﬁcally, believed positions of

all objects the utility functions depend on. This infor-

mation is sent with a frequency of 10Hz

Message delay has a direct impact on the coopera-

tive behaviour, since received data are integrated into

the belief base regardless of the message’s age. This

is done intentionally, to foster the conclusions we can

draw from experimental data. The initial allocations

of newly entered plans are protected by discarding

contradicting messages for 250ms. This ensures that

a calculated allocation has a minimal life cycle, and is

not immediately overwritten by delayed messages.

Our approach was evaluated in the robotic soccer

domain. The evaluation presented here is two-fold.

First we present results obtained in a simulated en-

vironment, with unreliable network due to packet loss

or delay. Delay and packet loss were artiﬁcially added

for clean results. Second, we present results obtained

under real-world conditions during the RoboCup ’09.

In the simulation, six agents play soccer coopera-

tively. In order to have reproducible results, there is

no opponent team. The sole plan with a dynamic util-

The frequency is chosen as to keep the network load

low.

TOWARDS A COMPREHENSIVE TEAMWORK MODEL FOR HIGHLY DYNAMIC DOMAINS

125

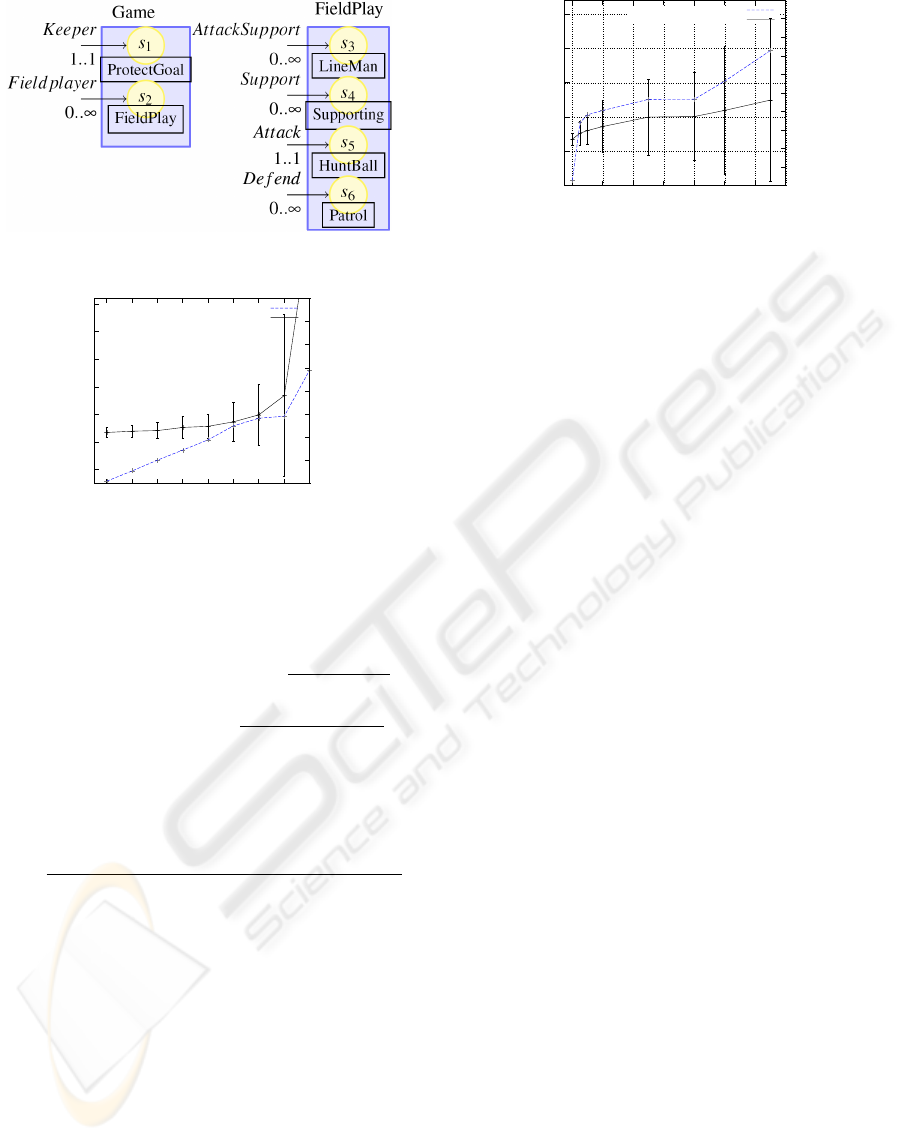
Figure 2: Simple Example Plan in the Soccer Domain.

-500

500

1000

1500

2000

2500

0 10 20 30 40 50 60 70 80

1.25

1.5

1.75

2.25

2.5

2.75

Average Time To Coordinate (ms)

Average Belief Count

Packet Loss (%)

Average time

Average belief count

Figure 3: Average Times To Coordinate and Average Belief

Count with Packet Loss.

ity function (U

) in this test is depicted in Figure 2.

= 0.1Pri + 1.0 max

x∈Attack

(1 −

Dist(x, Ball)

FieldSize

)

+0.2 max

y∈De f end

(1 −

Dist(y, OwnGoal)

FieldSize

)

where FieldSize refers to the maximal possible dis-

tance on the football ﬁeld. Pri sums over the prefer-

ences of each agent’s roles towards their tasks.

Pri =

∑

τ∈Tasks(p)

∑

In(x,p,τ,z)

max

HasRole(x,r)

Pref(r, τ)

∑

τ∈Tasks(p)

∑

In(x,p,τ,z)

We use two measures, “Time To Coordinate”

(TTC) refers to the average length of the time inter-

vals, the team was in disagreement about the allo-

cation within plan FieldPlay. “Belief Count” (BC)

refers to the average number of different allocations

believed by at least one robot. In the used data,

the average frequency of events requiring an alloca-

tion change was about 7.8 per minute. The simulator

caused these events by resetting the ball’s position.

Figure 3 illustrates the inﬂuence of packet loss on

the two measures. Under perfect conditions, TTC

is 177ms, with a standard deviation of 89ms. BC is

1.028 with standard deviation of 0.22. TTC slowly

increases till packet loss is at 50%, at which point

TTC is at 370ms with standard deviation of 352ms.

-500

500

1000

1500

2000

0 200 400 600 800 1000 1200 1400

1.1

1.2

1.3

1.4

1.5

1.6

1.7

1.8

1.9

Average Time To Coordinate (ms)

Average Belief Count

Packet Delay (ms)

Average time

Average belief count

Figure 4: Average Times To Coordinate and Average Belief

Count with Packet Delay.

Beyond this point, the curve steepness increased. At

80% packet loss, TTC is already at 3894ms and co-

ordination hardly occurs any more. Note that the

standard deviation of TTC follows the same pattern.

This is due to the increasing likelihood that two dis-

agreement intervals overlap and the increasing noise,

which introduces additional small disagreement pe-

riods. The belief count on the other hand proves to

be more resistant against packet loss, it grows linear

with the amount of packet loss. The same holds for

its standard deviation, which reaches 1.0 at 60% loss.

The relationship between packet delay and the

two measures is shown in Figure 4. Packet delay

was introduced with a uniformly distributed noise in

[−25ms, 25ms]. After an initial steep ascend of both

TCC and BC in the interval from 0ms to 50ms delay,

both measures grow only slowly with additional de-

lay. At 50ms, TTC is 263ms with a standard deviation

of 177ms, and BC equals 1.34 with standard devia-

tion of 0.7. Afterwards, deviation of BC stays almost

constant while the deviation of TTC continues to rise.

Again, this is due to intervals overlapping and delayed

messages inducing short periods of disagreement.

The most interesting fact here is the initial ascend

of the two measures. This indicates a beneﬁt of dis-

carding messages older than a certain time span, as

the data indicate a delay of 100ms is as bad as packet

loss of 40%. Note that, when in disagreement, the

robots still act, at no point in time a robot did not try to

fulﬁl a task. In summary, with disagreement periods

of 177ms under perfect conditions, 370ms under 50%

packet loss, and 361ms under 200ms delay, we can

state that the agents not only react quickly to changes

in the environment but also achieve agreement about

the task allocation quickly and hence act and cooper-

ate according to the modelled plans.

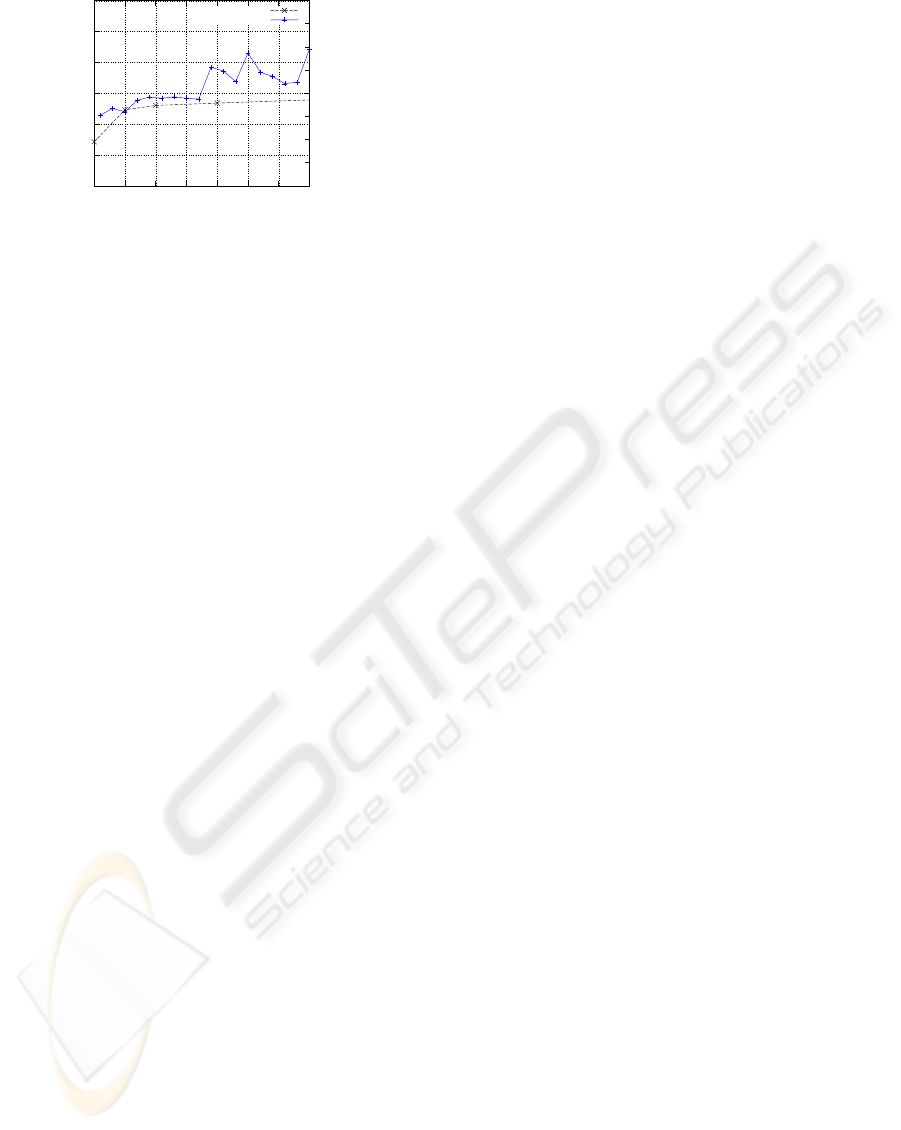
Figure 5 shows the average belief count during ac-

tual soccer matches. The data are normalised by the

number of robots involved. For comparison, simula-

tion results are shown as well. The data was gathered

from 226.6 minutes of game play. Unfortunately, the

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

126

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0 50 100 150 200 250 300 350

1.25

1.5

1.75

2.25

2.5

2.75

Average Belief Count per Robot

Average Belief Count

Average Packet Delay (ms)

WC 2009

Simulation

Figure 5: Normalised Average Belief Count vs Packet De-

lay during RC 2009.

network quality ﬂuctuated to quickly to draw mean-

ingful TTC values from the data collected. In aver-

age, a disagreement lasted for 300ms, i.e., 3 commu-

nication cycles. They occurred 22.8 times per minute.

Hence, in 11% of the time, a disagreement over the al-

location existed. Given the dynamic character of the

domain, reﬂected by the fact that each robot modi-

ﬁed its plan base to accommodate a new situation 17.5

times per minute, we deem this acceptable.

Compared with the simulation, the conditions are

harder, as the game is faster and much more dynamic.

Also, sensor noise degrades the coherence of informa-

tion used for team coordination. Especially in close-

quarter situations, our robots disregarded communi-

cated data in favour for local sensor data. This led to

breakdowns in the teamwork. Hence, it is imperative

to use fused information only for task allocations in

order to guarantee resolution of such conﬂicts.

However, the average belief count during the

RoboCup corresponds to the simulation data, even

though the plans employed during the RC were

more complex. Not only allocated the robots them-

selves within one plan, but also did they choose au-

tonomously the same plan out of a plan type. In gen-

eral, three plans were available on the level of Field-

Play, two defensive and one aggressive. This is a

small indicator that the approach scales well with the

complexity of the employed plans. A situation from

an actual game displaying dynamic allocations can

be found under http://www.youtube.com/watch?

v=3V_vedh95kc.

6 CONCLUSIONS

In this paper, we sketched a new language for describ-

ing multi-agent plans together with an operational se-

mantics. This language is geared towards highly dy-

namic domains in which agents have to take decisions

under tight time constraints. Such domains often oc-

cur in robotic scenarios. We presented how agents can

estimate their team mates’ decisions, act upon them,

and correct them when new information is available.

We showed experimentally that this approach is ro-

bust against a high degree of packet loss and delay,

common properties of communication in robotic sce-

narios.

Several open questions remain. It is still unclear

how coordination is affected if several domain prop-

erties, which are not observable by all agents, are used

for utility and condition calculations. We believe that

the approach employed by STEAM, namely commu-

nicating failures together with their reason, is a suit-

able method to foster coordination in this case. Fi-

nally, an embedding of ALICA into 3APL is work in

progress.

REFERENCES

Bratman, M. (1987). Intentions, Plans, and Practical Rea-

son. Harvard University Press.

Grosz, B. J. and Kraus, S. (1996). Collaborative plans

for complex group action. ARTIFICIAL INTELLI-

GENCE, 86(2):269–357.

Grosz, B. J. and Sidner, C. L. (1990). Plans for discourse.

In Intentions in Communication. MIT Press.

Hindriks, K. V., Boer, F. S. D., Hoek, W. V. D., and Meyer,

J.-J. C. (1999). Agent programming in 3APL. Au-

tonomous Agents and Multi-Agent Systems, 2(4):357–

401.

Levesque, H. J., Cohen, P. R., and Nunes, J. H. T. (1990).

On Acting Together. In Proc. of AAAI-90, pages 94–

99, Boston, MA.

Pynadath, D. V., Tambe, M., and Chauvat, N. (1999).

Toward team-oriented programming. In Intelligent

Agents VI: Agent Theories, Architectures, and Lan-

guages, pages 233–247.

Skubch, H., Wagner, M., and Reichle, R. (2009). A lan-

guage for interactive cooperative agents.

Tambe, M. (1997). Towards ﬂexible teamwork. Journal of

Artiﬁcial Intelligence Research, 7:83–124.

TOWARDS A COMPREHENSIVE TEAMWORK MODEL FOR HIGHLY DYNAMIC DOMAINS

127