MULTI-AGENT VOTING FOR CONFLICT RESOLUTION

A Fuzzy Approach

Miklos Nagy

Knowledge Media Institute, The Open University, Milton Keynes, United Kingdom

Maria Vargas-Vera

Computing Department, The Open University, Milton Keynes, United Kingdom

Keywords:

Multi-agents, Fuzzy systems, Voting, Conﬂict resolution.

Abstract:

Software agents that interpret the possible meaning of Semantic Web data differently should be able to resolve

their differences i.e. resolve conﬂicts effectively. One typical use case is ontology mapping where different

agents using different similarity measures create beliefs in the assessed similarities, which needs to be com-

bined into a more coherent state. The combination of these contradicting beliefs can easily worsen the mapping

precision and recall, which leads to poor performance of any ontology mapping algorithm. In these scenarios

agents, which use different similarities and combine them into a more reliable and coherent view can easily

become unreliable when these contradictions are not managed effectively between the different agents. In this

paper we propose a solution based on the fuzzy voting model for managing such situations by introducing

trust and voting between software agents that resolve contradicting beliefs in the assessed similarities.

1 INTRODUCTION

The continuously increasing semantic meta data on

the Web will soon make it possible to deploy multi-

agent systems on the Semantic Web that are able to in-

tegrate data from distributed and heterogeneous data

sources. However a prerequisite for these systems is

that agents deployed to different domains can develop

a certain degree of understanding of their data and

are able to map their data with other agents. There-

fore ontology mapping (Euzenat and Shvaiko, 2007)

is a key component of agent systems that need to in-

tegrate semantic data, which alone has several chal-

lenges(Shvaiko and Euzenat, 2008) before one can

develop real word applications. One of these chal-

lenges is how to handle conﬂicting information that

stems from the interpretation of Semantic Web data.

The source of conﬂict can range from missing or

insufﬁcient information to the contradicting descrip-

tion of the same or similar terms. As an example

consider two ontologies, which describe conferences.

Both contain concepts about the location of the event

where Ontology 1 contains the concept “Location” in

the context of the “Event” whereas Ontology 2 con-

tains “Place” in the context of the “Building”, “Ses-

sion room” or “Conference hall”. Considering the ex-

tended contexts of these terms e.g. Wordnet hyper-

nyms one can derive that both describes some kind of

space or position of something. The trouble is that this

information cannot be explicitly derived from the on-

tologies as “Place” refers to buildings and their parts,

while “Location” refers to geographical region (coun-

try or city) where the conference is held. In order to

resolve this contradiction human experts can discuss

their point of view and reach a consensus if the map-

ping can be made or not. Multi-agent systems that

create ontology mapping operate without human in-

tervention therefore need to mimic the before men-

tioned conﬂict resolution process, which can improve

the quality of the mapping if the contradiction can ef-

fectively be resolved. Our main contribution in this

paper is managing conﬂicting beliefs using a fuzzy

voting model and present a comparison using differ-

ent membership functions for resolving conﬂict be-

tween beliefs in similarities, which is the core com-

ponent of the DSSim ontology mapping system.

The paper is organized as follows. Section 2 pro-

vides the description of the problem and its context.

Section 3 describes the voting model and how it is ap-

plied for determining trust during the ontology map-

178

Nagy M. and Vargas-Vera M. (2010).

MULTI-AGENT VOTING FOR CONFLICT RESOLUTION - A Fuzzy Approach.

In Proceedings of the 2nd International Conference on Agents and Artiﬁcial Intelligence - Artiﬁcial Intelligence, pages 178-183

DOI: 10.5220/0002701301780183

 SciTePress

ping. Section 4 gives and overview of the related

work. Finally, section 5 describes our future work.

2 BELIEF COMBINATION AND

CONFLICTS

2.1 Combination of Similarity Measures

In the context of the Semantic Web it is envisioned

that multi-agent systems can interpret and exchange

the available data in order to achieve a speciﬁc task

e.g. map concepts from different data sources be-

fore answering a user query. It is unlikely that one

agent can haveall the algorithmsto determine similar-

ities alone therefore more agents are neccessary with

utilising different similarity measures that need to be

combined into a more coherent view. This trend can

be noticed in nearly all the systems that participate

in the OAEI

. Most of the participating systems are

not based on a multi-agent architecture however they

all utilise different similarity measures. Once the dif-

ferent similarities have been assessed they are com-

bined into a single measure which in turn is used to

determine to select the best possible mapping pairs.

The description of how mapping systems determine

or built up beliefs in similarities and how systems de-

termine semantic similarity are out of the scope of

this paper nevertheless each system is described in the

OAEI papers

. The system that inspired our work is

called DSSim which uses a multi-agent architecture

to build up beliefs in similarities and combines them

using the Demster combination rule.

2.2 Source of Conﬂict

In our domain of interest namely ontology mapping

several challenges had been identiﬁed by Shvaiko and

Euzenat(Shvaiko and Euzenat, 2008), which are con-

sidered as major roadblocks for developing ontology

mapping solutions that perform well on different do-

mains. We have identiﬁed two problems that are the

main source of contradictions when algorithms need

to “interpret” the meaning of the data represented by

the different ontologies. These problems are as fol-

lows:

1. Representation Problems and Uncertainty.

Data on the semantic web is represented by on-

tologies, which typically consist of a number of

classes, relations, instances and axioms. These

http://oaei.ontologymatching.org/

http://om2008.ontologymatching.org/

elements are expressed using a logical language.

The W3C has proposed RDF(S)(Beckett, 2004)

and OWL(McGuinness and Harmelen, 2004) as

Web ontology language however OWL has three

increasingly-expressive sublanguages(OWL Lite,

OWL DL, OWL Full) with different expressive-

ness and language constructs. In addition to

the existing Web ontology languages W3C has

proposed other languages like SKOS(Miles and

Bechhofer, 2008), which is a standard to sup-

port the use of knowledge organization systems

(KOS) such as thesauri, classiﬁcation schemes,

subject heading systems and taxonomies within

the framework of the Semantic Web. SKOS are

based on the Resource Description Framework

(RDF) and it allows information to be passed be-

tween computer applications in an interoperable

way. Ontology designers can choose between

these language variants depending on the intended

purpose of the ontologies. As a result of these

representation differences ontology mapping sys-

tems will always need to consider the uncertain

and conﬂicting aspects of how the semantic web

data can be interpreted and processed by different

similarity algorithms.

2. Quality of Semantic Web Data. Data quality

problems (Wang et al., 1993) (Wand and Wang,

1996) in the context of database integration(Batini

et al., 1986) have emerged long before the Se-

mantic Web concept has been proposed. For ev-

ery organisation or individual the context of the

data, which is published can be slightly different

depending on how they want to use their data.

Therefore from the exchange point of view in-

completeness of a particular data is quite com-

mon. The problem is that fragmented data envi-

ronments like the Semantic Web inevitably lead

to data and information quality problems causing

the applications that process this data deal with ill-

deﬁned inaccurate or inconsistent information on

the domain. In traditional integration scenarios re-

solving these data quality issues represents a vast

amount of time and resources for human experts

before any integration can take place. Software

agents that operate on the Semantic Web need to

resolve semantic data quality problems indepen-

dently from the users.

As a result it is important that multi-agent systems on

the Semantic Web can resolve their conﬂicting inter-

pretation that stem from the above mentioned prob-

lems.

MULTI-AGENT VOTING FOR CONFLICT RESOLUTION - A Fuzzy Approach

179

3 FUZZY VOTING MODEL FOR

ONTOLOGY MAPPING

3.1 Voting and the Best Possible

Alternative

The idea of individual voting in order to resolve con-

ﬂict and choose the best option available is not rooted

in computer but political science. Democratic sys-

tems are based on voting as Condorcet jury theorem

(Austen-Smith and Banks, 1996) (Young, 1988) pos-

tulates that a group of voters using majority rule is

more likely to choose the right action than an arbitrary

single voter is. In these situations voters have a com-

mon goal, but do not know how to obtain this goal.

Voters are informed differently about the performance

of alternative ways of reaching it. If each member of

a jury has only partial information, the majority de-

cision is more likely to be correct than a decision ar-

rived at by an individual juror. Moreover, the proba-

bility of a correct decision increases with the size of

the jury. But things become more complicated when

information is shared before a vote is taken. People

then have to evaluate the information before making

a collective decision. The same ideas apply for soft-

ware agents especially if they need to reach a consen-

sus on a particular issue. In case of ontology mapping

where each agent can built up beliefs over the cor-

rectness of the mappings based on partial information

we believe that voting can ﬁnd the socially optimal

choice. Software agents can use voting to determine

the best decision for agent society but in case voters

make mistakes in their judgments, then the majority

alternative (if it exists) is statistically most likely to be

the best choice. The application of voting for software

agents is a possible way to make systems more intel-

ligent i.e. mimic the decision making how humans

reach consensus decision on a problematic issue.

3.2 Fuzzy Voting Model

In ontology mapping the conﬂicting results of the dif-

ferent beliefs in similarity can be resolved if the map-

ping algorithm can produce an agreed solution, even

though the individual opinions about the available al-

ternatives may vary. Fuzzy voting model is detailed

in (Nagy et al., 2008) can be utilised for reaching this

agreement by evaluating trust between established be-

liefs through voting, which is a general method of rec-

onciling differences. Voting is a mechanism where

the opinions from a set of votes are evaluated in order

to select the alternatives that best represent the collec-

tive preferences. Unfortunately deriving binary trust

like trustful or not trustful from the difference of be-

lief functions is not so straightforward since the dif-

ferent voters express their opinion as subjective prob-

ability over the similarities. For a particular mapping

this always involves a certain degree of vagueness

hence the threshold between the trust and distrust can-

not be set deﬁnitely for all cases that can occur during

the process. Additionally there is no clear transition

between characterising a particular belief highly or

less trustful. Therefore our argument is that the trust

membership or belief difference values, which are

expressed by different voters can be modeled prop-

erly by using fuzzy representation. Before each agent

evaluates the trust in other agent’s belief over the cor-

rectness of the mapping it calculates the difference be-

tween its own and the other agent’s belief. Depending

on the difference it can choose the available trust lev-

els e.g. if the difference in beliefs is 0.2 then the avail-

able trust level can be high and medium. We model

these trust levels as fuzzy membership functions. In

fuzzy logic the membership function µ(x) is deﬁned

on the universe of discourse U and represents a par-

ticular input value as a member of the fuzzy set i.e.

µ(x) is a curve that deﬁnes how each point in the U

is mapped to a membership value (or degree of mem-

bership) between 0 and 1. Our ontology mapping sys-

tem models the conﬂict resolution as a fuzzy system

where the system componentsare described in the fol-

lowing sections:

3.3 Fuzziﬁcation of Input and Output

Variables

Fuzziﬁcation is the process of decomposing a system

input and/or output into one or more fuzzy sets. We

have experimented different types of curves namely

the triangular, trapezoidal and gauss shaped member-

ship functions. Each fuzzy set spans a region of in-

put (or output) value graphed with the membership.

Our selected membership functions overlap to allow

smooth mapping of the system. The process of fuzzi-

ﬁcation allows the system inputs and outputs to be ex-

pressed in linguistic terms so that rules can be applied

in a simple manner to express a complex system.

Deﬁnition 1. Belief difference is an input variable,

which represents the agents own belief over the cor-

rectness of a mapping in order to establish map-

pings between concepts and properties in the ontol-

ogy. During conﬂict resolution we need to be able to

determine the level of difference.

We propose three values for the fuzzy membership

value µ(x) = {small, average, large}.

Deﬁnition 2. Belief is an input variable, which de-

scribed the amount of justiﬁed support to A that is

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

180

the lower probability function of Dempster, which ac-

counts for all evidence E

that supports the given

proposition A.

belief

(A) =

∑

⊆A

) (1)

where m Demster’s belief mass function represents

the strength of some evidence i.e. m(A) is our ex-

act belief in a proposition represented by A. The

similarity algorithms itself produce these assignment

based on different similarity measures. We propose

three values for the fuzzy membership value ν(x) =

{weak, strong}.

Deﬁnition 3. Similarity is an input variable and is the

result of some syntactic or semantic similarity mea-

sure. We propose three values for the fuzzy member-

ship value ξ(x) = {low, average, high}.

Deﬁnition 4. Low, medium and high trusts are out-

put variables and represent the level of trust we can

assign to the combination of our input variables. We

propose three values for the fuzzy membership value

τ(x) = {low, medium, high}.

3.4 Rule Set

Fuzzy sets are used to quantify the information in

the rule-base, and the inference mechanism oper-

ates on fuzzy sets to produce fuzzy sets. Fuzzy

systems map the inputs to the outputs by a set of

condition− > action rules i.e. rules that can be ex-

pressed in I f −Then form. For our conﬂict resolution

problem we have deﬁned four simple rules that ensure

that each combination of the input variables produce

output on more than one output i.e. there is always

more than one initial trust level is assigned to any in-

put variables. As an example consider a rule for cases

when the trust level is deﬁned as low:

“IF ( beliefdifference IS large OR beliefdifference

IS average ) AND belief IS weak AND (similarity IS

low OR similarity IS average ) THEN trust IS low”

The rules we have initially deﬁned are the most

general ones. In our future research we intend to in-

vestigate the impact of more ﬁne grained rules (i.e.

more rules could be deﬁned to cover overlapping ar-

eas of our fuzzy sets) on our conﬂict resolution.

3.5 Defuzziﬁcation Method

After fuzzy reasoning we have the linguistic output

variables, which need to be translated into a crisp ( i.e.

real numbers, not fuzzy sets) value. The objective is

to derive a single crisp numeric value that best repre-

sents the inferred fuzzy values of the linguistic output

variable. Defuzziﬁcation is such inverse transforma-

tion, which maps the output from the fuzzy domain

back into the crisp domain. In our ontology mapping

system we have selected the Center-of-Area (C-o-A)

defuzziﬁcation method. The C-o-A method is often

referred to as the Center-of-Gravity method because

it computes the centroid of the composite area repre-

senting the output fuzzy term. In our system the trust

levels are proportional with the area of the member-

ship functions therefore other defuzziﬁcation meth-

ods like Center-of-Maximum (C-o-M) or Mean-of-

Maximum (M-o-M) does not correspond well to our

requirements.

Deﬁnition 5. For representing trust in beliefs over

similarities we have deﬁned three membership func-

tions, χ(x) = {low, average, high}.

3.6 Possible Membership Functions for

Conﬂict Resolution

For our conﬂict resolution problem we have carried

out experiments in order to select the best possible

membership function combination that ﬁt well to our

problem. We have chosen the trapezodial, triangular

and gauss membership function and their combina-

tions to represent our input and output variables. For

each test have generated 300 scenarios, which contain

random input variables (belief difference, belief and

similarity) that maps to a single trust level i.e. output

variable(high, medium or low trust). In addition we

have deﬁned nine combination of membership func-

tions that describes our input and output variables. We

repeated our experiment 1000 times regenerating the

300 scenarios in each iteration.

3.7 Results on the Use of Different

Memberships Functions

Experiments have shown that the the fuzzy conﬂict

resolution is really sensitive on the input membership

function. The best results can be achieved using tri-

angular membership functions. In each experiments

the average wrong answers are 121 and the minimum

wrong answers are 109 whereas the maximum are 134

when choosing triangular input functions. The re-

sults are promising as we are able to resolve conﬂict

in nearly 2/3 of the cases. In practice the real im-

provements in the ontology mapping quality can be

foreseen where the number of conﬂict for the candi-

date mapping set is high. These situation of course

likely to occur where both source and target ontolo-

gies contain large number (up to 10.000) of concepts

and properties. The selection of the output function

MULTI-AGENT VOTING FOR CONFLICT RESOLUTION - A Fuzzy Approach

181

does not inﬂuence the end result of the conﬂict reso-

lution.

4 CASE STUDY

We have carried out experiments with the benchmark

ontologies of the Ontology Alignment Evaluation Ini-

tiative(OAEI)

, which is an international initiative

that has been set up for evaluating ontology match-

ing algorithms. The experiments were carried out to

assess how trust management inﬂuences results of our

mapping algorithm. Our main objective was to evalu-

ate the impact of establishing trust before combining

beliefs in similarities between concepts and properties

in the ontology. The OAEI benchmark contains tests,

which were systematically generated starting from

some reference ontology and discarding a number of

information in order to evaluate how the algorithm

behave when this information is lacking. The bibli-

ographic reference ontology (different classiﬁcations

of publications) contained 33 named classes, 24 ob-

ject properties, 40 data properties. Further each gen-

erated ontology was aligned with the reference ontol-

ogy. The benchmark tests were created and grouped

by the following criteria:

• Group 1xx: simple tests such as comparing the

reference ontology with itself, with another irrel-

evant ontology or the same ontology in its restric-

tion to OWL-Lite.

• Group 2xx: systematic tests that were obtained by

discarding some features from some reference on-

tology e.g. name of entities replaced by random

strings, synonyms, name with different conven-

tions, strings in another language than english, hi-

erarchy that can be suppressed, expanded or ﬂat-

tened.

• Group 3xx: four real-life ontologies of biblio-

graphic references that were found on the web e.g.

BibTeX/MIT, BibTeX/UMBC.

As the benchmark is the only test-set in the OAEI

tracks where the results are also available we have run

ﬁrst our experiments where DSSim applies the fuzzy

voting model for evaluating trust and one without it.

Therefore as a basic comparison we have modiﬁed

our algorithm (without trust), which does not evaluate

trust before conﬂicting belief combination just com-

bine them using Dempster’s combination rule. The

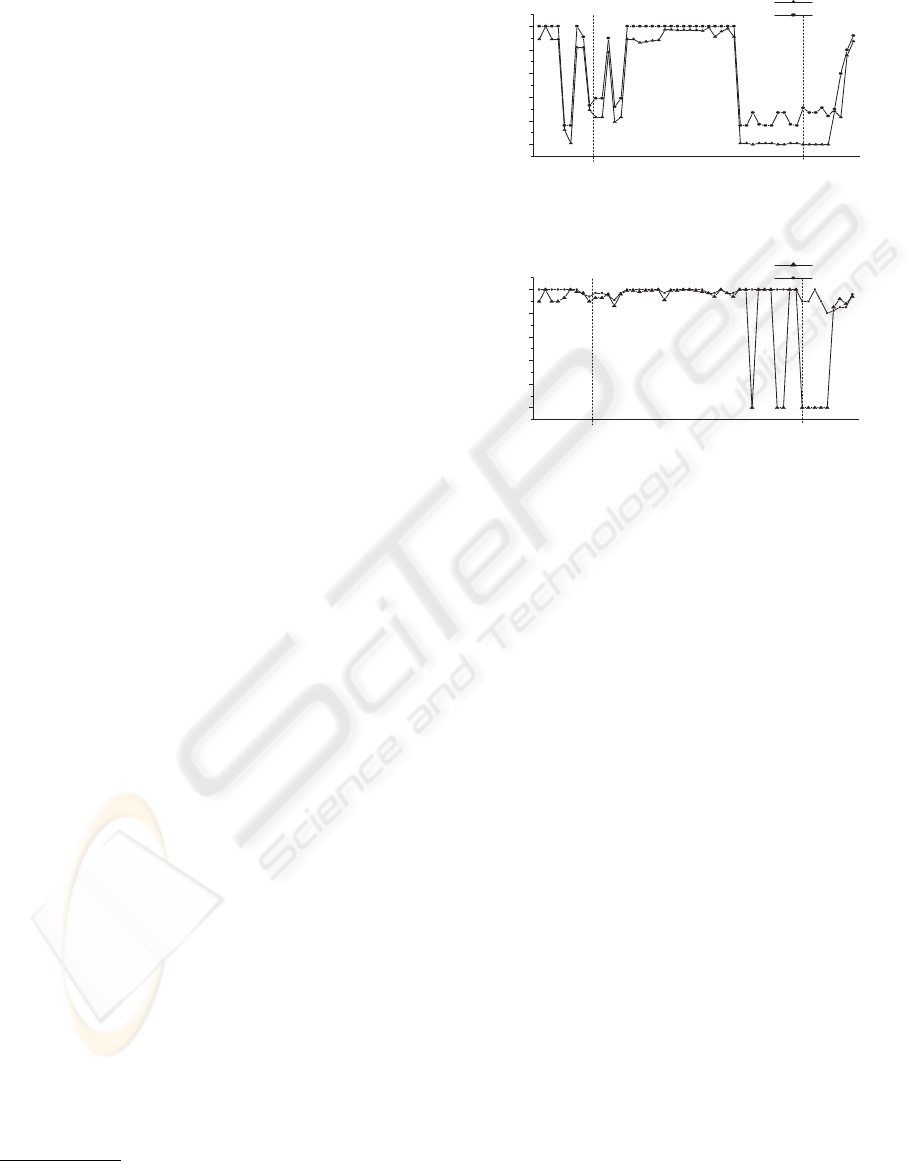
recall and precision graphs for the algorithm with

trust and without trust over the whole benchmarks are

depicted on Fig. 1, 2. Experiments have proved that

http://oaei.ontologymatching.org/

with establishing trust one can reach higher average

precision and recall rate.

0.0

0.2

0.4

0.6

0.8

1.0

3xx

2xx1xx

Recall

Benchmarks

Without trust

With trust

Figure 1: Recall graph with and without applying fuzzy vot-

ing.

0.0

0.2

0.4

0.6

0.8

1.0

3xx

2xx1xx

Precision

Benchmarks

Without trust

With trust

Figure 2: Precision graph with and without applying fuzzy

voting.

5 RELATED WORK

Different approaches to eliminate contradictions for

ontology mapping have been proposed by the ontol-

ogy mapping community. These approaches can be

classiﬁed into two distinct categories. First group in-

clude solution that considers uncertainty and fuzzi-

ness as an inherent nature of the ontology mapping

and tries to describe it accordingly. Ferrera et. al.

(Ferrara et al., 2008) models the whole ontology map-

ping problem as fuzzy where conﬂicts can occur.

Their solution use fuzzy Description Logic theories

to the problem of mapping validation as a different

way of handling mapping uncertainty with respect to

probabilistic approaches. As a result, they propose

a mapping validation algorithm based on fuzzy inter-

pretation of mappings in order to detect inconsisten-

cies. Tang et.al. (Tang et al., 2006) formalises the on-

tology mapping problem as the problem of Bayesian

decision making as strategy. Their sytem RiMOM

has participated in the OAEI competition since 2006.

Their solution do consider two kinds of conﬂicts in

metadata heterogeneity, structure conﬂict and name

conﬂict. However they use thesaurus and statistical

techniques to resolve them before combining the re-

sults. The second group however differ conceptually

because they mainly utilise data mining and logic rea-

soning techniques in pre and post processing stages of

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

182

the mapping. Liu et.al. (Liu et al., 2006) proposes

a four-stage ontology mapping approach with inte-

grating the available information of labels, instances,

past experiences, and the structures in different stages

gradually. Besides, reusing the past experiences, re-

ducing the aggregation-level mismatch before itera-

tion, mining the logic relation of attributes account

for the improvement of mapping results thus eliminat-

ing the available contradictions. Similar solution has

been proposed by the ASMOV system (Jean-Mary

and Kabuka, 2008) , which automates the ontology

alignment process using a weighted average of mea-

surements of similarity along four different features

of ontologies, and performs semantic validation of re-

sulting alignments. This system acknowledges that

conﬂicting mappings are produced during the map-

ping process but they use an iterative post processing

logic validation in order to ﬁlter out the conﬂicting

mappings.

6 CONCLUSIONS

In this paper we have shown how the fuzzy voting

model can be used to resolve contradictory beliefs be-

fore combining them into a more coherent state by

evaluating fuzzy trust. The main contribution of this

paper is managing conﬂicting beliefs using different

fuzzy variables and to present a comparison using

different membership functions and fuzzy variables

for resolving conﬂict between beliefs in similarities,

which is the core component of the DSSim ontology

mapping system. We have proposed new levels of

trust for resolving these conﬂicts in the context of on-

tology mapping, which is a prerequisite for any sys-

tems that makes use of information available on the

Semantic Web. Our system is conceived to be ﬂex-

ible because the membership functions for the vot-

ers could be changed dynamically in order to inﬂu-

ence the outputs according to the different similar-

ity measures that can be used in the mapping sys-

tem. We have described initial experimental results

with the benchmarks of the Ontology Alignment Ini-

tiative, which demonstrates the effectiveness of our

approach through the improved recall and precision

rates. There are many areas of ongoing work, with our

primary focus considering the effect of the changing

number of voters and the impact on precision and re-

call or applying our algorithm in different application

areas. We also aim to measure the proportion of the

obvious and difﬁcult conﬂicts that can occur during

the mapping process and how these affect the overall

performance of our solution.

REFERENCES

Austen-Smith, D. and Banks, J. S. (1996). Information ag-

gregation, rationality, and the condorcet jury theorem.

The American Political Science Review, 90(1):34–45.

Batini, C., Lenzerini, M., and Navathe, S. B. (1986). A

comparative analysis of methodologies for database

schema integration. ACM Computing Surveys,

18(4):323–364.

Beckett, D. (2004). Rdf/xml syntax speciﬁcation,

http://www.w3.org/rdf/.

Euzenat, J. and Shvaiko, P. (2007). Ontology matching.

Springer-Verlag, Heidelberg (DE).

Ferrara, A., Lorusso, D., Stamou, G., Stoilos, G., Tzou-

varas, V., and Venetis, T. (2008). Resolution of con-

ﬂicts among ontology mappings: a fuzzy approach.

In Proceedings of the 3rd International Workshop on

Ontology Matching.

Jean-Mary, Y. R. and Kabuka, M. R. (2008). Asmov: Re-

sults for oaei 2008. In Proceedings of the 3rd Interna-

tional Workshop on Ontology Matching.

Liu, X.-J., Wang, Y.-L., and Wang, J. (2006). Towards a

semi-automatic ontology mapping - an approach us-

ing instance based learning and logic relation min-

ing. In Fifth Mexican International Conference (MI-

CAI 2006) on Artiﬁcial Intelligence.

McGuinness, D. L. and Harmelen, F. V. (2004). Owl

web ontology language, http://www.w3.org/tr/owl-

features/.

Miles, A. and Bechhofer, S. (2008). Skos simple knowl-

edge organization system, http://www.w3.org/tr/skos-

reference/.

Nagy, M., Vargas-Vera, M., and Motta, E. (2008). Manag-

ing conﬂicting beliefs with fuzzy trust on the semantic

web. In The 7th Mexican International Conference on

Artiﬁcial Intelligence (MICAI 2008).

Shvaiko, P. and Euzenat, J. (2008). Ten challenges for on-

tology matching. Technical Report DISI-08-042, Uni-

versity of Trento.

Tang, J., Li, J., Liang, B., Huang, X., Li, Y., and Wang, K.

(2006). Using bayesian decision for ontology map-

ping. Web Semantics: Science, Services and Agents

on the World Wide Web, 4(243–262).

Wand, Y. and Wang, R. Y. (1996). Anchoring data quality

dimensions in ontological foundations. Communica-

tions of the ACM, pages 86–95.

Wang, R. Y., Kon, H. B., and Madnick, S. E. (1993). Data

quality requirements analysis and modeling. In Pro-

ceedings of the Ninth International Conference on

Data Engineering, pages 670–677.

Young, H. P. (1988). Condorcet’s theory of voting. The

American Political Science Review, 82(4):1231–1244.

MULTI-AGENT VOTING FOR CONFLICT RESOLUTION - A Fuzzy Approach

183