DOCUMENTS REPRESENTATION BASED ON INDEPENDENT

COMPRESSIBILITY FEATURE SPACE

Nuo Zhang and Toshinori Watanabe

Graduate School of Information Systems, The University of Electro-Communications

1-5-1, Chofugaoka, Chofu-shi, Tokyo, Japan

Keywords:

Documents representation, PRDC, Independent component analysis, Feature space, Clustering, Data com-

pression.

Abstract:

There are two well-known feature representation methods, bag-of-words and N-gram models, which have

been widely used in natural language processing, text mining, and web document analysis. A novel Pattern

Representation scheme using Data Compression (PRDC) has been proposed for data representation. The

PRDC not only can process data of linguistic text, but also can process the other multimedia data effectively.

Although PRDC provides better performance than the traditional methods in some situation, it still suffers

the problem of dictionary selection and construction of feature space. In this study, we propose a method

for PRDC to construct an independent compressibility space, and compare the proposed method to the two

other representation methods and PRDC. The performance will be compared in terms of clustering ability.

Experiment results will show that the proposed method can provide better performance than that of PRDC and

the other two methods.

1 INTRODUCTION

Text classiﬁcation technique is widely used in many

ﬁelds, including scientiﬁc research, commerce ap-

plication, etc. By adopting the text classiﬁcation

technique, documents can be searched more accurate

(Richard O. Duda and Stork, 2001). Documents can

be classiﬁed according to their relative importance or

appearance frequency of words. When handling a

large number of e-documents, a good classiﬁer can

improve efﬁciency.

Text classiﬁcation performance is also dependent

on the choice of feature sets. The vector space model

is a well known method for text feature extraction and

representation. It represents the content of a docu-

ment as a vector, and each word in the document is

used as a content unit. There are several methods pro-

posed for text representation in the manner of vec-

tor space model so far. Bag-of-words (BOW) (Lewis,

1998) and N-gram models (Cavnar, 1994) are two of

the most popular methods in text retrieval, for their

simpleness and high performance. In these methods,

documents are often represented as high dimensional

feature, such as thousands of sparse vectors and only

a tiny part of them signiﬁcantly affect the efﬁciency

and the results of the mining process.

Recently, for multimedia data including sound,

image and text, a method named PRDC (Pattern Rep-

resentation Scheme Using Data Compression) (Toshi-

nori Watanabe and Sugihara, 2002) is developed to

uniformly perform analysis. It shows some effec-

tive results that are similar to the other two ap-

proaches, and outperformsthem in some applications.

PRDC represents the feature of data as compress-

ibility vectors. The measurement for all kinds of

data is the distance among the vectors. PRDC can

be combined with clustering and classiﬁcation meth-

ods. However, the performance of PRDC is depen-

dent on how to choose characteristic axes to construct

a vector space. PRDC suffers from the dimensional-

ity problem caused by incorrectly chosen dictionar-

ies. Luckily, there are a lot of methods were pro-

posed for dimension reduction (Yin Zhonghang and

Qian, 2002), (Liu Ming-ji and Yi-mei, 2002). Bar-

man, P.C., et al. have proposed a non-negative ma-

trix factorization based text mining (P. C. Barman and

Lee, 2006). In which, after extracting the uncorre-

lated basis probabilistic document feature vectors of

the word-document frequency, classiﬁcation is per-

formed. They found very high accuracy when applied

their approach to Classic3 dataset. Mao-Ting Gao, et

al. have approached in a different way, which is based

217

Zhang N. and Watanabe T. (2010).

DOCUMENTS REPRESENTATION BASED ON INDEPENDENT COMPRESSIBILITY FEATURE SPACE.

In Proceedings of the 2nd International Conference on Agents and Artiﬁcial Intelligence - Artiﬁcial Intelligence, pages 217-222

DOI: 10.5220/0002704402170222

 SciTePress

on projection pursuit (Gao and Wang, 2007). The idea

is founded on linear and non-linear structures and fea-

tures of the original high-dimensional data can be ex-

pressed by its projection weights in the optimal pro-

jection direction. Their results showed that it was ef-

fective to cluster texts. A new semi-supervised di-

mension reduction proposed by Martin-Merino, M.,

et al. is a textual data analysis method (Martin-

Merino and Roman, 2006). The Semi-supervised di-

mension reduction means exploiting manually cre-

ated classiﬁcation of a subset of documents. Re-

cently, dimension reduction based on independent

component analysis (ICA) shows better performance

(Shaﬁei et al., 2007), which uses ICA to select inde-

pendent feature vectors.

In this study, we focus on the selection of charac-

teristic axes for PRDC. The text representation abil-

ity of the proposed method is compared with bag-

of-words and N-gram models, for which, we use

the methods to construct vector feature for several

benchmark datasets respectively. A popular cluster-

ing method, called k-means, is employed to examine

the representation results. Based on experiment re-

sults, we will show the performance of the proposed

method comparing to the other two methods.

2 THE PROPOSED METHOD

AND THE TRADITIONAL

METHODS

In this section, we ﬁrst introduce the pattern represen-

tation scheme using data compression (PRDC). Then

we show how to choose characteristic axes for PRDC.

2.1 Pattern Representation Scheme

using Data Compression

In this study, data compression is used for represen-

tation of documents. In general, a model of input in-

formation source is used for encoding the input string

in data compression. And a compression dictionary

is used as the model. The compression dictionary is

automatically produced when compressing input data,

eg. Lempel-Ziv (LZ) compression (Ziv and Lempel,

1978). In the same way, PRDC constructs a compres-

sion dictionary by encoding input data forms. It pro-

duces a compressibility vector space from the com-

pression dictionary to project new input data into it.

Therefore, we can get the feature of data represented

by a compressibility vector. Finally, PRDC classiﬁes

data by analyzing these compressibility vectors.

Subsequently, PRDC is used as follows for rela-

tion analysis of similar documents. The compression

dictionaries constitute a compressibility vector space.

The compressibility vector space can be represented

by a compressibility table, which is made by project-

ing the input document into the compressibility vec-

tor space. Let N

be the input document. By com-

pressing the input document, a compression dictio-

nary is obtained, which is expressed as D

. Com-

pressing document N

by D

, we get compression

ratio C

. Where, L

is the size of the in-

put stream N

, K

is the size of the output stream.

Compressing with all of the dictionaries, we obtain

a compressibility vector for each input document. In

the compressibility table, the columns show the doc-

ument data N

, the rows show the compression dic-

tionary D

formed by the same document, and the

elements show the compressibility C

[%]. PRDC

utilizes this table to characterize documents.

2.2 The Proposed Method

In PRDC a compressibility vector space (dictionary

space) is constructed by randomly choosing dictionar-

ies. This method is simple to implement and provides

comparative performance. However, it is impossible

to know how many dictionaries to be selected and

where they are in the data space in this manner. An

appropriate selection of dictionaries for PRDC to im-

prove its representation performance is needed. Gen-

erally the method of dictionary selection in PRDC,

may be considered as selection of dictionaries from a

few large clusters in the data space. A large cluster

occupies a big area, in which the randomly selected

dictionaries may not represent the cluster properly, if

one or more chosen dictionaries are at the edge of the

cluster. The larger the clusters become, the larger the

select bias is.

Small clusters can be considered to be ’pure’.

Randomly selected dictionaries are able to make a

representative feature space in small clusters. This se-

lection provides the number of dictionaries to select

and where to select dictionaries. When the size of

dataset becomes large, the number of the aforemen-

tioned pure clusters will increase and consequently

the number of selected dictionaries will increase.

Hence, this method also suffers the curse of dimen-

sionality problem when dataset becomes large, which

is a well known problem when handling data analysis.

We propose to use ICA to improve the vector

space construction which can represent input doc-

uments properly in our method, since it produces

spatially localized and statistically independent basis

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

218

vectors. The proposed method is implemented as fol-

lows. First some dictionaries are randomly selected

to build a dictionary space. Based on which the in-

put documents are separated into a large number of

clusters to obtain small and pure ones. Then, one

document is randomly selected from each cluster to

construct dictionaries and a new dictionary space is

constructed. The input documents are compressed to

obtain a compressibility matrix in the new dictionary

space.

Let X be the compressibility matrix obtained from

X = AS, (1)

where S is a matrix consisted of input documents,

and A is a feature transform matrix. As a prepro-

cess before ICA, singular value decompositon (SVD)

is used to reduce the dimension of X. After which,

by estimating W = A

−1

in equation

S = WX itera-

tively using an ICA algorithm called JADE (Jean-

Francois Cardoso and SOULOUMIAC, 1996), the in-

dependent dictionaries can be obtained. Using the se-

lected dictionaries we can construct a new compress-

ibility space.

Note it is not guaranteed that which document

and its corresponding dictionary are important, be-

cause there is no order or ranking in the independent

components after using ICA as a dimension reduc-

tion method. We order the documents according to

the norms of the columns of the matrix W. Conse-

quently, it is able to know the corresponding dictio-

naries. These dictionaries are selected to construct

a compressibility space. A better performance can

be obtained by using the new compressibility vector

space to represent documents.

Our proposed method is also adapted to remove

stop words noise based on the consideration of the

words (or segments), which are closed to the origin,

as stop words. Those words are compressed by all of

the dictionaries. In this way, the proposed method can

process a dataset intensively.

3 EXPERIMENTS

In order to evaluate the performance of PRDC, bag-

of-words, N-gram model and the proposed method, a

popular clustering method called k-means is used to

classify the four datasets based on each of the above

four methods. And purity is used to show the perfor-

mance of each method.

Purity measures the extent to which each cluster

contains documents from primarily one class (Zhao

and Karypis, 2002). The overall purity of a clustering

solution is deﬁned as the weighted sum of individual

cluster purities:

Purity =

∑

r=1

(

)P(S

) (2)

where P(Sr) is the purity for a particular cluster of

size n

, k is the number of clusters and d is the total

number of data items in the dataset. Purity of a single

cluster is deﬁned by P(S

) = n

, where n

is the

number of documents in cluster r that belong to the

dominant (majority) class in r, i.e., the class with the

most documents in r. Obviously, the higher the pu-

rity value is, the purer the cluster in terms of the class

labels of its members is, and the better the clustering

results becomes.

In the following sections, the implementation of

N-gram models, bag-of-words model, PRDC and the

proposed method are introduced in details. Also, the

datasets for the comparison are introduced.

3.1 Document Representation Methods

• Bag-of-words Model. In the preprocessing pro-

cedure, the white spaces, newlines, and tabs are

replaced by a single space. Non-alphabetical

characters are also replaced by a single space. Up-

per case characters are all converted to lower case.

As a result, every document is divided into a bag

of words based on spaces. And all stop words

are removed based on the standard van Rijsbergen

stop word list. After that, each word is stemmed

by using Porter’s Stemmer. And any word which

appears in four documents or less in the dataset

is removed. At last, the weight of each word in a

document is calculated using the standard TF-IDF

(Term Frequency-Inverse Document Frequency).

For comparison, the feature vector for each docu-

ment is normalized to unit length.

• N-gram Model. In the preprocessing procedure,

the white spaces, newlines, and tabs are replaced

by a single space. Non-alphabetical characters are

also replaced by a single space. Upper case char-

acters are all converted to lower case. N-gram

model for any documents is realized. Then, every

N-gram which does not appear in most documents

is removed from N-gram model. The weight of

each N-gram in each document is calculated by

using the standard TF-IDF. In the same way with

bag-of-words model, the feature vector for each

document is normalized to unit length.

• PRDC. In the preprocessing procedure, the white

spaces, newlines, and tabs are replaced by a sin-

gle space. Non-alphabetical characters are also re-

DOCUMENTS REPRESENTATION BASED ON INDEPENDENT COMPRESSIBILITY FEATURE SPACE

219

placed by a single space. Upper case characters

are all converted to lower case. As a result, every

document is divided to a series of segments based

on spaces. A small number of documents are

randomly selected and compressed to construct a

compressibility space. The derived dictionaries

are used to compress all of the documents and ob-

tain a compressibility vector for each document.

In the same way, the feature vector for each docu-

ment is normalized to unit length.

• The Proposed Method. The processing proce-

dure is the same with that of PRDC, except for

reconstructing compressibility vector space by us-

ing our proposed method as described perviously.

Furthermore, in the compressibility vector space,

a word (segment) which is near to the original

point is considered as stop word (segment). All

stop words (segments) are removed from docu-

ments.

3.2 Data Collections

In this study, we use several benchmark datasets to

evaluate the proposed method and the traditional doc-

ument representation approaches. The benchmark

datasets are CLASSIC3, URCS and Reuters-21578.

In order to examine all the representation methods for

Japanese documents, we collected some news from

ceek.jp newswire.

• CLASSIC3. This dataset is comprised of 3891

abstracts from 3 disjoint research ﬁelds. They

are aeronautical system papers (Cranﬁeld: 1398

abstracts), medical papers (Medline: 1033 ab-

stracts), and information retrieval papers (CISI:

1460 abstracts).

• URCS (University of Rochester Computer Sci-

ence Technical Reports). This dataset consists of

609 abstracts from 4 categories.

Artiﬁcial Intelligence: 119 items,

Robotics: 97 items,

Systems: 218 items,

Theory: 175 items.

They are all derived from computer science. And

a fair amount of shared terminology between the

categories is expected.

• A Subset of Reuters-21578. This dataset consists

of 21578 news appeared on the Reuters newswire

in 1987. The documents were assembled and in-

dexed with categories by personnel from Reuters

Ltd. and Carnegie Group, Inc. Reuters-21578

is currently the most widely used test collection

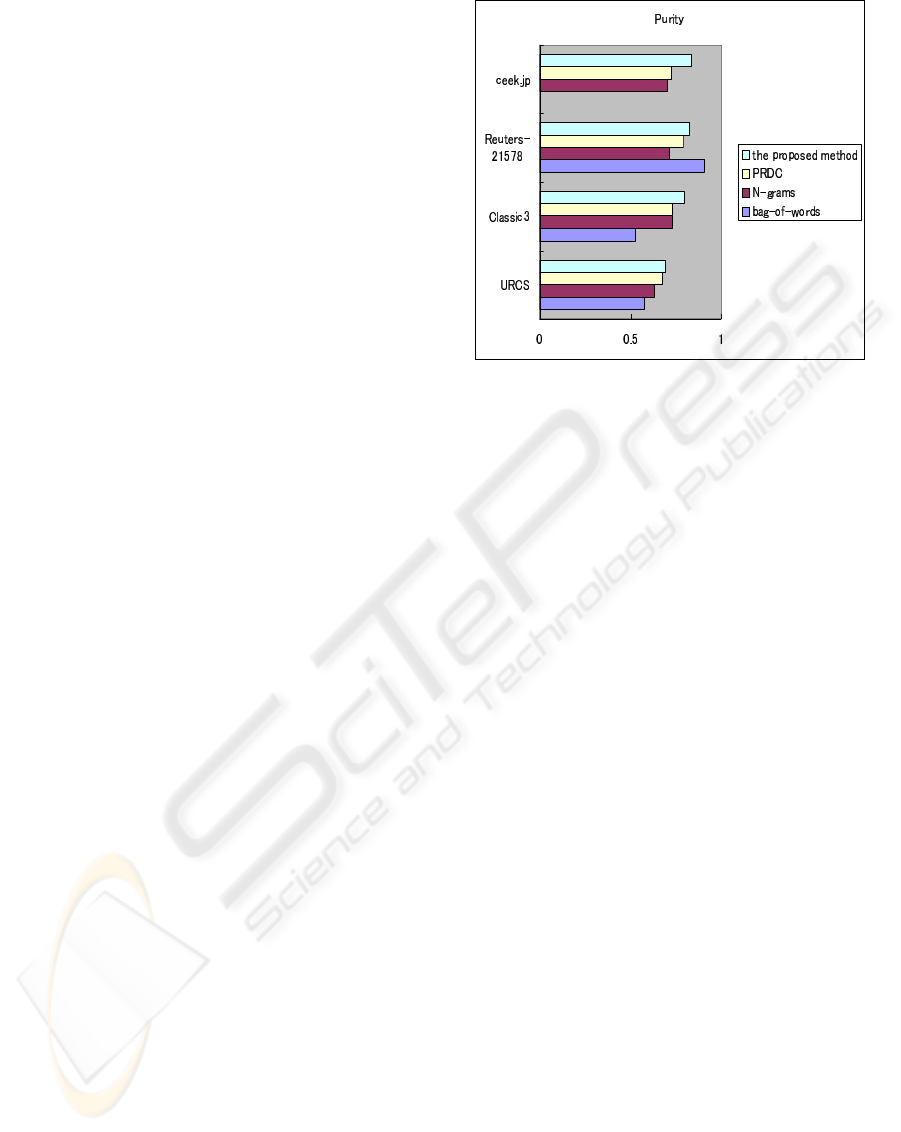
Figure 1: Comparison of the proposed method, PRDC, bag-

of-words and N-gram.

in information retrieval, machine learning, and

other corpus-based research. Since the dataset

contains some noise, such as repeated documents,

unlabeled documents, and empty documents, we

choose a subset of 10 relatively large groups (acq,

coffee, crude, earn, interest, money-fx, money-

supply, ship, sugar, and trade) of 9295 documents

in our experiments. For each of the articles in the

10 categories that will be used, only the text bod-

ies are extracted.

• A Subset Downloaded from ceek.jp. This

dataset consists of 300 Japanese news from a

newswire ceek.jp in Jun 2008. They are news in

IT (100 items), sports (100 items), and politics

(100 items). The ceek.jp news is used by many

researchers for evaluating their algorithms’ per-

formances when processing Japanese documents.

3.3 Comparison with using Small-Scale

Data Sets

In this experiment, we compare the performance

of bag-of-words, N-gram, PRDC and our proposed

method with using small-scale subsets extracted from

ceek.jp (45items(= 15× 3)), URCS (60items(= 15×

4)), CLASSIC3 (45 items (= 15 × 3)) and Reuters-

21578 datasets (500items(= 50× 10)) respectively.

The results are shown in Fig. 1. For Classic3

and ceek.jp datasets, PRDC showed similar purity

with N-gram model, whereas the proposed method

showed better performance than that of the two meth-

ods. For URCS and Classic3 datasets, the proposed

method showed better performance than that of all

the other methods. For Reuters-21578, the proposed

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

220

method was better than N-gram and PRDC methods.

In this case, bag-of-words method provided the best

performance. For ceek.jp dataset, the performance of

the proposed method was better than that of N-gram

and PRDC methods. Since morphological analysis is

required for bag-of-word model processing Japanese

documents, the result of it is not shown in this study.

For all the datasets, the proposed method provided

better performance than that of PRDC.

From the observation in Fig. 1, we can see that

the proposed method averagely showed better per-

formance comparing with the other methods when

processing relatively small-scale datasets. Although,

for Reuter-21578, a large number (500) of docu-

ments was extracted, and bag-of-words model was

able to provide correspondingly better representation

for documents in this case, when the number of doc-

uments was small, there was no much data to be

used to construct the document feature for represen-

tation. The purity of bag-of-words model had big

change in this experiment. In this case, the bag-of-

words and N-gram models suffered from severely de-

grade. The proposed method was more robust, be-

cause an independent compressibility vector space is

constructed for each dataset. The proposed method

provided better performance both in processing En-

glish and Japanese datasets without working with a

stop list. In contrast, bag-of-words model failed to

process Japanese documents without extra process-

ing. The experiments also showed that the proposed

method outperformed PRDC, with ICA to reduce di-

mension and select independent feature vectors.

3.4 Comparison with using Large-Scale

Data Sets

In this experiment, we compare the performance

of bag-of-words, N-gram, PRDC and the proposed

method with using large scale (full size) datasets.

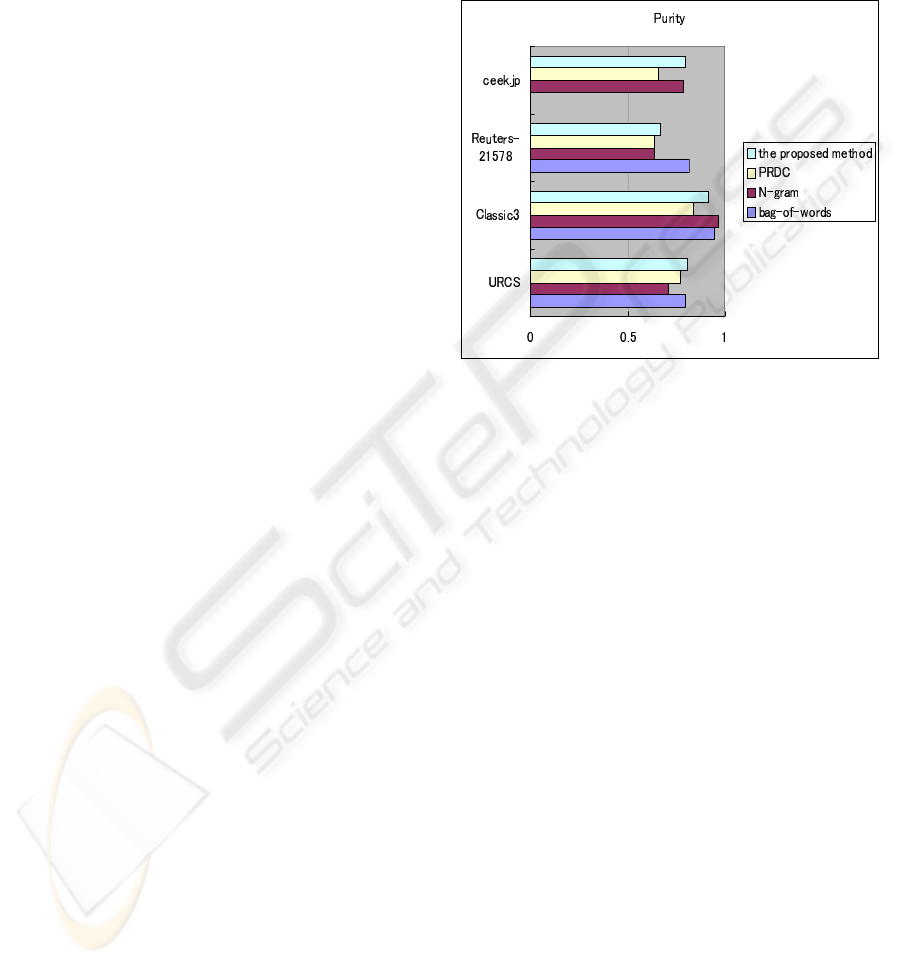
The results are shown in Fig. 2. For URCS

dataset, both PRDC and the proposed method showed

better performance than that of N-gram model. The

proposed method also showed better performance

than that of bag-of-words model. For ceek.jp news,

we only compared the proposed method with PRDC

and N-gram model, since the bag-of-words model

cannot process Japanese without extra morphological

analysis. The results showed that the performance of

the proposed method was better than that of N-gram

model. Without independent compressibility vector

space and removal of stop words, PRDC provided the

lowest purity result in the rank of processing Japanese

documents. For Reuters-21578, bag-of-words model

was more accurate than the proposed method and N-

gram model, because the large number of documents

and repeated words helped bag-of-words to feature

documents. However, the proposed method showed

better performance than that of PRDC and N-gram

model with constructing a independent feature space.

For Classic3 dataset, the performance of the proposed

method was similar to the other two methods.

Figure 2: Comparison of the proposed method, PRDC, bag-

of-words and N-gram.

For all the datasets the proposed method pro-

vided better representation ability than that of PRDC.

The proposed method averagely showed better per-

formance comparing with bag-of-words and N-gram

models when the scale of dataset is relatively small.

Also the proposed method provided similar perfor-

mance with bag-of-words and N-gram models in pro-

cessing Classic3 dataset.

4 CONCLUSIONS

In this study we introduced our proposed method and

compared it with bag-of-words, N-gram models and

PRDC. The proposed method does not need a stop

list. Furthermore, the proposed method represents

data in an independent feature space and provides

good performance. The comparison results of the

proposed method and all other thress methods by us-

ing ceek.jp, URCS, CLASSIC3 and Reuters-21578

dataset was implemented. Our proposed method

showed generally good performance in each compar-

ison experiment. The future work for the proposed

method is in processing large scale and complicated

dataset.

DOCUMENTS REPRESENTATION BASED ON INDEPENDENT COMPRESSIBILITY FEATURE SPACE

221

ACKNOWLEDGEMENTS

This research was partially supported by the Ministry

of Education, Science, Sports and Culture, Grant-in-

Aid for Scientiﬁc Research (C), 19500076, 2009.

REFERENCES

Cavnar, W. B. (1994). Using an n-gram-based docu-

ment representation with a vector processing retrieval

model. TREC-3: text retrieval conference, pages 269–

277.

Gao, M.-T. and Wang, Z.-O. (2007). A new algorithm for

text clustering based on projection pursuit. Sixth In-

ternational Conference on Machine Learning Cyber-

netics, 6:3401–3405.

Jean-Francois Cardoso, J.-f. C. C. and SOULOUMIAC, A.

(1996). Jacobi angles for simultaneous diagonaliza-

tion. SIAM J. Mat. Anal. Appl, 17:161–164.

Lewis, D. D. (1998). Naive (bayes) at forty: The indepen-

dence assumption in information retrieval. Proceed-

ings of ECML-98, 10th European Conference on Ma-

chine Learning, 1398:4–15.

Liu Ming-ji, W. X.-f. and Yi-mei, R. (2002). Feature acquir-

ing algorithm on the web text. Mini-Micro Systems,

23(6):683–686.

Martin-Merino, M. and Roman, J. (2006). A new semi-

supervised dimension reduction technique for textual

data analysis. Intelligent Data Engineering and Auto-

mated Learning - IDEAL 2006. 7th International Con-

ference. Proceedings, 4224:654–662.

P. C. Barman, N. I. and Lee, S.-Y. (2006). Non-negative ma-

trix factorization based text mining: feature extraction

and classiﬁcation. Neural Information Processing.

13th International Conference, ICONIP 2006. Pro-

ceedings, Part II, 4233:703–712.

Richard O. Duda, P. E. H. and Stork, D. G. (2001). Pattern

classiﬁcation (2nd edition). John Wiley and Sons.

Shaﬁei, M. Singer Wang Zhang, R. M. et al. (2007). Docu-

ment representation and dimension reduction for text

clustering. 2007 IEEE 23rd International Conference

on Data Engineering Workshop, pages 770–779.

Toshinori Watanabe, K. S. and Sugihara, H. (May. 2002).

A new pattern representation scheme using data com-

pression. IEEE TransPAMI, 24(5):579–590.

Yin Zhonghang, Wang Yongcheng, C. W. and Qian, D.

(2002). A comparative study on two techniques of

reducing the dimension of text feature space. Journal

of Systems Engineering and Electronics, 13(1):87–92.

Zhao, Y. and Karypis, G. (2002). Criterion functions for

document clustering: Experiments and analysis. Tech-

nical Report TR, Department of Computer Science,

University of Minnesota,Minneapolis, MN.

Ziv, J. and Lempel, A. (1978). Compression of individual

sequence via variable-rate coding. Information The-

ory, IEEE Transactions on, 24(5):530–536.

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

222