
AN EFFICIENT ALGORITHM TO ESTIMATE REAL-TIME
TRAFFIC INFORMATION BASED ON MULTIPLE DATA SOURCES
Du Bowen, Liang Yun, Ma Dianfu, Lv Weifeng and Zhu Tongyu
State Key Laboratory of Software Development Environment, Beihang University, Beijing, China
Keywords:
Real-time traffic information, Dempster-Shafer theory, Real-time traffic information fusion algorithm, Real-
time floating car system, Quality of data.
Abstract:
Gathering traffic congestion information from all available sources to provide real-time traffic information not
only makes reliable traffic predictions for management center, but also supports travelers to help guiding their
transit decision. However, the key issue is that the quality of existing multiple traffic data sources are uncertain,
and how to use them for performing trusty travel time estimation is a question. In this paper, a novel algorithm
is proposed to address this problem. Firstly, through analyzing large amounts of traffic data, the reliability
of evidence and its relationship with road network are defined in spatio-temporal dimension. Secondly, after
using an improved aggregation method based on Dempster-Shafer evidence theory, the optimized evidences
are adopted to estimate each link’s average link travel time. Comparative experiments of the real test-vehicle
scheduling signals and real-time system data (supported by some 15000 floating cars and 320 loop detectors)
indicate that the new algorithm is proved to be both reasonable and practical. It can be applied in real-time
systems to manage large amount of data.
1 INTRODUCTION
The Real-Time Traffic Information (RTTI) plays a
more and more important role in modern society.
Through RTTI, the travelers can obtain optimized
routes and traffic information before traveling, which
can make them keep away from block roads and acci-
dents (Aomori, 1999). In other words, using RTTI to
travel can make process of their trip more economic
and effective, among which the actual Average Link
Travel Time (ALTT) is a basic component of it. How-
ever, how to solve data stability and data accuracy of
ALTT becoming the key issue of current research.
Fortunately, the information fusion technology
has been developed and introduced to solve the prob-
lem.On the one hand, using inductive Loop Detectors
(LDs) to collect data are the most widely used means
nowadays because of the maturity of the inductance
technique, and the most important advantage of LDD
is their stability (Pushkar A, 1994). On the other hand,
by using large amount of floating cars to obtain ALTT
is considered as one of the most efficient and promis-
ing methods. Based on data from numerous floating
cars, travel time at divided Road sections(links) can
be calculated directly (Corrado de Fabritiis, 2008).
In this paper, Real Time Traffic Information
Fusion Algorithm (RTTIFA) is proposed. Firstly,
through providing appropriate dynamic weights for
each piece of traffic data, the real time floating car
data(FCD) and loop detector data (LDD) are opti-
mized. Secondly, a method based on modified D-S
theory in order to classify the evidence is addressed.
Finally, according to a decision rule, the valid data is
selected to estimate traffic state and ALTT.
2 STATISTICAL DATA ANALYSIS
Extensive deployment of loop detectors is able to
provide tremendous amount of baseline data for real
system, it is a kind of statistic data. For each loop
detector,there several statistical results are estimated
in a sampling interval(the sampling interval is 5min
in practice, and amount sampling interval of 24 hours
is 288), each of them is viewed as a piece of LDD.
In the review of literatures, we know that stability is
its key point (Petty, 1998), so γ
j
k
′′
is used to adapt the
weight of loop detector LD
k
′′
.
507
Bowen D., Yun L., Dianfu M., Weifeng L. and Tongyu Z. (2010).
AN EFFICIENT ALGORITHM TO ESTIMATE REAL-TIME TRAFFIC INFORMATION BASED ON MULTIPLE DATA SOURCES.
In Proceedings of the 2nd International Conference on Agents and Artificial Intelligence - Artificial Intelligence, pages 507-510
DOI: 10.5220/0002705405070510
Copyright
c
SciTePress

It can be expressed as:
γ
j
k
′′
=
|speed
k
′′
− ALTS
′
j
|
max{speed
k
′′
, ALTS
′
j
}
, k
′′
= 1, 2, . . . K
′′
(1)
Where speed
k
′′
describes the speed value of LD
k
′′
in the last sampling interval. ALTS
′
j
is the average
link travel speed of link j in previous sampling inter-
val. K
′′
is the sample size of LD
k
′′
in current sampling
interval.
Using floating cars, real-time OD data can be ob-
tained. From the point of view of urban road network,
the length of link is relativelyshort and most of the ve-
hicle tracks are constituted by two or more road links
in the urban network, thus the calculated average ve-
locities above should be distributed spatially to these
road links. So in our method,the weight value of each
track is definited (Qing-jie Kong and Liu, 2007). It
not only consider travel information of track k’ which
cover current link, but also consider travel informa-
tion of track k’ on its adjacent links. That is,
γ
j
k
′
=
∑
J
j=1
D
j
∑
J
j=1
l
j
, k
′
= 1, 2, . . . K
′
(2)
Where
∑
J
j=1
D
j
describes the traveled distance of
track k’ on link l
j
and its adjacent links,
∑
J
j=1
l
j
de-
scribes the overall length of these links. The number
of tracks which covered link l
j
is the sample size and
express as K’.
3 APPLICATION OF D-S
EVIDENCE THEORY IN DATA
FUSION
The general goal of our method is to acquire real-time
and accurate ALTT of each link in road network. In
this section, we utilize an improved evidence theory
for data classification. Firstly, traffic status are di-
vided into three levels: jam (speed≤20 km/h), slow
(20 km/h < speed ≤ 40 km/h) and smooth (speed
> 40km/h). Each one is viewed as a classification
and an element of the frame of discernment. That is,
Θ = { jam, slow, smooth} The power set is:
2
Θ
= {⊘, { jam}, {slow}, {smooth}, { jam, slow},
{slow, smooth}, { jam, smooth}, { jam, slow, smooth}
Among these, A =
{{ jam}, {slow}, {smooth}}, ∀A
f
∈ A is single-
tons set. At the same time, because we are not
sure which singleton the evidence belong to, so
B = {{ jam, slow}, {slow, smooth}}, ∀B
g
∈ B is
defined as the set of uncertain sets; { jam, smooth}, ⊘
are meaningless, { jam, slow, smooth} is an unknown
set.
In a sampling interval, each link has been labeled
by several velocities of different vehicles and loop de-
tectors. Every track or a piece of LDD is defined as
an evidence and express as t. The basic probability as-
signment, or mass function, assigns some quantity of
belief to the elements of the frame of discernment. In
our algorithm, m(C
z
) is the measure of the belief as-
signed by support degree of a evidence t
k
, which can
be assigned as:
m(C
z
) =
γ
N
′
∀C
z
∈ 2
Θ
(3)
Where γ is the weight of an evidence , N’ is the
sample size of evidence set in the current sampling
interval.
The belief Bel(A
f
) measures the degree given by
a source support the belief in a specified element as
the right answer. It is given by:
Bel
j
(A
f
) =
∑
m(A
f
) ∀A
f
∈ A (4)
The plausibilityPl(A
f
) measures how much we
should believe in an element if all unknown belief is
assigned to it. So we comprehensivelytake account of
the information of all the surrounding evidences that
in the edge transition area: uncertain set is assigned
by the evidence which the labeled in the edge transi-
tion area.
Pl(A
f
) =
∑
C
z
∩A
f
6=⊘
m(C
z
) ∀A
f
∈ A,C
z
∈ 2
Θ
(5)
At last, we define m(Θ) as:
m(Θ) =
N
′
∑
k=1
1− γ
k
N
′
(6)
Where N’ is the sample size of evidences set.
4 ALGORITHM DESCRIPTION
In this section, there are two critical procedures: one
is data cluster based on D-S theory, the other is the
method for decision rule.
4.1 Evidence Classification
It is tricky that assorted evidences from different
IDs generally share some common road link, while
declaring disparate average velocities on it. A prac-
tical way is to optimize all these distributed velocity
contributions on the road link as well as their corre-
sponding weight factors into account integrated, then
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
508

formulate a reasonable result.In other words, the set
of evidence can be optimized as:
Ω
j
= {t
k
|
γ(t
k
)
γ(t
k,max
)
≥ G}, k = 1, 2, . . . N (7)
Where γ(t
k,max
) express which has the best weight
value among γ(t
k
), Ω
j
is the optimized set of link l
j
,
G is threshold value.
The classification strategy on evidence is based on
its support degree to singletons. So the classification
of each evidence k is defined according to the labeled
value of γ
j
. However, when the labeled value is near
the dividing lines (such as 20 km/h) among the traf-
fic condition levels, it should allocate proper support
value to the uncertain propositions. In our algorithm,
we set edge transition area (near the traffic state divid-
ing lines) to solve this problem. In a simplified illus-
tration in Figure 1, V
s
is the step size, the size of tran-
sition area is 2δ, and the threshold of dividing lines v
d
are valued as v
jam−slow
d
= V
s
and v
slow− f ree
d
= 2V
s
.
To reduce uncertainty degree of evidence, the
Figure 1: Illustration the definition of dividing lines.
amounts and support degree of evidences to singleton
Bel
j
(A
f
) is defined as:
Bel
j
(A
f
) =
∑
m(A
f
) +
∑
B
g
∩A
f
6=⊘
m
′
(B
g
)
m
′
k
(B
g
) =
|speed
j
k
−v
d
|
δ
m
k
(B
g
)
|speed
j
k
− v
d
| < δ
(8)
Where speed
j
k
is the labeled speed of evidence k,
m(A
f
) is the measure of the belief assigned by a given
evidence to singleton with no doubt. m(B
g
) is the
measure of the belief assigned by a given evidence
(the labeled speed in the edge transition area).
4.2 Decision Rule
In view of literatures, Ying-Ming Wang (Wang, 2005)
brings forward a simple but more practical and more
rational preference ranking method. We apply this
algorithm to obtain the combined fusion result in the
Evidential Reasoning Framework. Meanwhile, we
do some modifications according to the need of our
application.
The approach is summarized as follows:
P
j
(A
f
> A
g
)=
max[0,Pl({A
f
})−Bel({A
f
})]−max[0,Bel({A
f
})−Pl({A
g
})]
[Pl({A
f
})−Bel({A
f
})]+[Pl({A
g
})−Bel({A
g
})]
(9)
Where ∀A
f
, A
g
∈ AThe degree of preference of A
f
over A
g
can be defined in the same way. It is obvious
that P
j
(A
f
) + P
j
(A
g
) = 1 and P
j
(A
f
) = P
j
(A
g
) = 0.5
when A
f
= A
g
. In this situation, we can make our
final estimats of the traffic state on each road link in
terms of which classification the evidence fall into.
5 EVALUATION
In order to verify the model presented in this paper,
we arrange some 200 test-cars to traveling along 10
scheduled routes in daytime and their every seconds
GPS data to be processed as actual value. Each route
tested 4 or 5 times by more than 50 test-cars.
In the experiment, we divide the scheduled route
into several parts, and record the time when the vehi-
cle travels passing the starting and the ending location
of every part. We describes the error rate of the results
as follows:
E =
|t
e
− t
a
|
t
a
(10)
Where t
e
escribes the travel time of some parts of
the route calculated from the system,t
a
describes the
actual travel time that we recorded from test-vehicles.
For testing weight of evidence, 3 different meth-
ods (simple average, link-based method and CR-
based method) were taken to sample selection and the
field data was collected from a path of XUEYUAN
road,Beijing, a part of one scheduled route which is a
typical road section in urban arteries.
19:02 19:22 19:42 20:02 20:22 20:22 20:42 21:02
0
20%
40%
60%
80%
100%
time
travel time error
Figure 2: Travel time error by RTFCS results.
AN EFFICIENT ALGORITHM TO ESTIMATE REAL-TIME TRAFFIC INFORMATION BASED ON MULTIPLE
DATA SOURCES
509
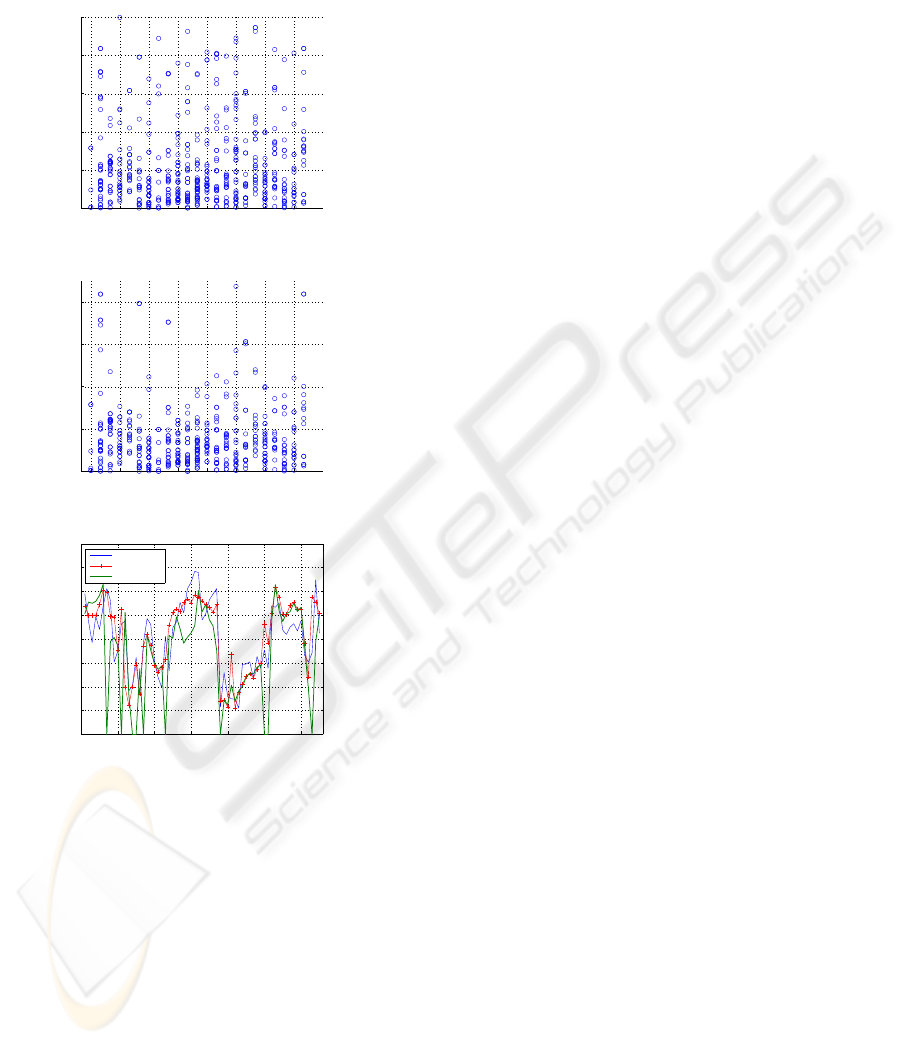
As a result, random sampling analysis was imple-
mented as mentioned in following. Each blue mark
’O’ expresses standard deviation by a floating car, and
the results were shown in Figure 2 to Figure 4.
19:02 19:22 19:42 20:02 20:22 20:22 20:42 21:02
0
20%
40%
60%
80%
100%
time
travel time error
Figure 3: Travel time error by link-based results.
19:02 19:22 19:42 20:02 20:22 20:22 20:42 21:02
0
20%
40%
60%
80%
time
travel time error
Figure 4: Travel time error by CR-based results.
0 10 20 30 40 50 60
0
10
20
30
40
50
60
70
80
link series
travel speed
By test vehicle
By RTTFA
By RTFCS
Figure 5: The difference in traveling speed.
The accuracy of them is evaluated by averaging
test-cars results. As we expected, the result of CR-
based expected to produce the most accurate result,
and Figure 4 confirms this by showing the lowest stan-
dard deviation for this method.
To evaluate the accuracy of our method, the follow-
ing experimentcompares the difference among travel-
ing speed provided by RTTFA results, RTFCS results
and test-cars results, and the results of comparison are
shown in Figure 5. It is obvious that for both stability
and accuracy, the performance of RTTIFA is better
than the results of RTFCS. In other words, utilizing
optimized evidence set to estimate ALTT, can ensure
the reliable of evidences and improve the accuracy of
RTTI.
6 CONCLUSIONS
In this paper, we present a novel algorithm for ac-
quiring link traffic information based on the merits
of LD and FCD. In order to achieve this task, we
established the relationship of contact evidences and
road network in spatio-temporal dimension at first,
and then we classify evidences by improved aggrega-
tion method based on Demoster-Shafer evidence the-
ory. By applying a decision rule, the ALTT of each
link is estimated at last. From the evaluation, the con-
clusion can be made that the algorithm proposed in
this paper can fully take advantage of the superiori-
ties of these two sources’ merits.
REFERENCES
Aomori, N. K. (1999). Prefectural travel time system
by using vehicle information and communicationsys-
tem (vics). In International Conference of Intelligent
Transportation Systems.
Corrado de Fabritiis, Roberto Ragona, G. V. (2008). Traffic
estimation and prediction based on real time floating
car data. In he 11th International IEEE Conference on
Intelligent Transportation Systems, Beijing, China.
Petty, K. F. (1998). Accurate estimation of travel times from
single-loop detectors. Transportation Research Part
A: Policy and Practice.
Pushkar A, F.L. Hall, J. A.-D. (1994). Estimation of speeds
from single-loop freeway flow and occupancy data us-
ing cusp catastrophe theory model. Transportation
Research Record.
Qing-jie Kong, Y. C. and Liu, Y. (2007). An improved evi-
dential fusion approach for real-time urban link speed
estimation. In IEEE Intelligent Transportation Sys-
tems Conference Seattle, WA, USA.
Wang, Y.-M. (2005). Computers and operations research.
In A preference aggregation method through the esti-
mation of utility.
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
510
