
SYNTHETIC IRIS IMAGES FROM IRIS PATTERNS BY MEANS OF
EVOLUTIONARY STRATEGIES
How to Deceive a Biometric System based on Iris Recognition
Alberto de Santos Sierra, Javier Guerra Casanova
Centro de Dom
´
otica Integral, Campus de Montegancedo, 28223 Pozuelo de Alarc
´
on, Madrid, Spain
Carmen S
´
anchez
´
Avila, Vicente Jara Vera
Applied Mathematics Department, ETSIT, Polytechnical University of Madrid, Madrid, Spain
Keywords:
Biometric iris recognition, Synthetic iris images, Iris falsification, Security, Evolutionary strategies.
Abstract:
Synthetic Biometric is emerging nowadays as a new research field in biometrics. An artificial iris tissue or a
synthetic fingerprint could compromise the security, allowing a non-registered individual to enter the system.
However, inverse biometric can also improve current identification systems, enhancing not only its strength
against fake-based attacks, but also by replicating unavailable or corrupted data, due to a bad acquisition, for
instance. The methods proposed in this document aim to provide a procedure to create a synthetic iris tissue
from a stored biometric template, so that a non-registered user could access the system under a registered
identity. These algorithms will come out with the result that synthetic sample could be so similar to original
as desired.
1 INTRODUCTION
Biometric systems based on Iris Recognition are
known to be one of the most reliable systems in terms
of security (Daugman, 1993; Daugman, 2004). Con-
sidering the fact that Iris is already stable in very early
stages of life and unalterable since that moment, it is
obviously impossible to modify the iris itself. Thus,
any method attempting to deceive a system based on
iris recognition should focus on the acquired image,
which is already stored in the system when captured.
Despite of being suggested that there exists no
previous development of an automated iris recon-
struction, (Yanushkevich, 2006), there is indeed a pre-
vious work on iris synthesis, (Cui et al., 2004), but
focused on creating synthetic biometric databases for
testing purpose, far beyond the scope provided in this
paper, where the aim consists on accessing the system
by means of synthetic iris images. On the other hand,
several attempts already exist in other biometric tech-
niques such as fingerprint (Capelli et al., 2006), face
recognition (Yanushkevich et al., 2007), handwritten
signature (Guyon, 1996; Yanushkevich, 2006), voice
(Cook, 2002), and so forth.
Overall biometric systems relies their strength on
the fact that once the templates are extracted, there is
no function able to find an acquisition, whatever its
nature (fingerprint, iris, hand veins), whose template
coincides with the required pattern.
This paper provides two approaches attempting to
implement such a function, i.e., a function able to
come out with an image iris, whose pattern may be
so similar to the desired template as required. Based
on evolutionary strategies, the procedure will provide
the best solution to meet the required goal. There-
fore, this algorithm may be extended to other biome-
tric techniques, and all biometric systems will benefit
of it, since their main applications consider not only
enhancing the system against fakes, but also impro-
ving its performance, by replicating corrupted data or
testing algorithms with synthetic databases.
2 CREATING A SYNTHETIC IRIS
The main problem this approach tackles with is about
creating an artificial iris tissue. In order to meet this
goal, two approaches have been implemented with a
twofold purpose: first, providing two possible solu-
tions, and second, comparing them in terms of visual
aspect and overall performance.
Each approach is based on evolutionary strategies
194
de Santos Sierra A., Guerra Casanova J., Sánchez Ávila C. and Jara Vera V. (2010).
SYNTHETIC IRIS IMAGES FROM IRIS PATTERNS BY MEANS OF EVOLUTIONARY STRATEGIES - How to Deceive a Biometric System based on
Iris Recognition.
In Proceedings of the Third International Conference on Bio-inspired Systems and Signal Processing, pages 194-201
DOI: 10.5220/0002706601940201
Copyright
c
SciTePress

(Eiben and Smith, 2003; Schwefel, 1995), but the
schemes on which they are based are completely dif-
ferent. Nonetheless, before describing the algorithms
in detail, the problem to be solved must be stated.
2.1 Problem Statement
The problem these two approaches attempt to tackle
with can be stated mathematically as a function A ,
whose input is the template of a user already regis-
tered in the database, T
RU
. More in detail, A can be
expressed as:
A : T 7−→ D
T ∈ T 7−→ A(T ) ∈ D
(1)
where T represents the set of all possible tem-
plates in a Biometric System, in other words, T is the
information stored in the biometric database, (Daug-
man, 2004); and D stands for the set of all possible
images of a given database, related to previous T .
Both sets verify to have the same number of elements,
same cardinality, and each element in T corresponds
to only one element in D, and vice-versa.
This paper will suppose that the information of the
database is available, but in most current systems, the
stored information is protected and encrypted, so un-
veiling patterns in T is an arduous, but possible, task.
As an overview, A is a function which provides
an image A(T) ∈ D when being applied to a template
T ∈ T .
Continuing on mathematical representation, Z is
defined as the algorithm responsible for extracting the
template from an image. In other words,
Z : D 7−→ T
I ∈ D 7−→ Z(I) ∈ T
(2)
In fact, Z(D) = T , because each element in T
corresponds to only one element in D.
Furthermore, a measure must be defined in order
to assess how similar two templates are. Let η ∈ R be
a function able to measure to what extend two tem-
plates coincides or not. This measurement can be de-
fined in terms of T as follows,
η : T × T 7−→ R
T
1
, T
2
∈ T 7−→ η(T
1
, T
2
)
(3)
For the sake of simplicity, η is implemented by
Euclidean distance in this document, but other mea-
sures can be deployed, (Gonz
´
alez et al., 2004). In any
case, η(T
1
, T
2
) will tend to zero, when T
1
tends to T
2
.
Finally, considering previous equations Eq. (1)-
(3), the main problem can be stated as:
Given T
RU
(a registered user template) and η
0
(a threshold), implement A in order to verify that
η(
e
T , T
RU
) ≤ η
0
, where
e
T = Z(A(T
RU
)). In other
words, the problem can be defined in terms of func-
tions as:
Attempt to find A so that A = Z
−1
.
Before dealing with the problem of finding A,
several constraints concerning Z should be made.
First of all, and for the sake of simplicity, Z will
be defined as in previous approaches (S
´
anchez-
´
Avila
and S
´
anchez-Re
´
ıllo, 2002; de Santos-Sierra et al.,
2007), losing some generality. This approach will
be explained in next section 2.2. However, the main
ideas are suitable not only for other feature extrac-
tors (Boles and Boashash, 1998; Chun and Chung,
2004; Daugman, 2004), but also for other biometric
techniques. Secondly, A has been tested in CASIA
v3 database (http://www.sinobiometrics.com), a low
quality database, so that, Z will provide low resolu-
tion templates. Testing these algorithms in different
databases, remains as a future work.
2.2 Template Description
Evidently, a falsification must consider how the tem-
plate is extracted, otherwise the problem could be
unattainable. The extraction step begins after pre-
processing the image, once the iris has been isolated
from pupil, eyelids, and so forth, (Daugman, 1993;
de Santos-Sierra et al., 2007). Furthermore, a first
‘raw’ template is extracted from the isolated iris, be-
ing afterwards processed in order to obtain a better
result in identification.
This approach regards only these previous ‘raw’
data, for the sake of simplicity. Note these consi-
derations do not lack of generality, since posterior
processing is inherent to each Biometric System, and
furthermore, such post-processing is easily reversible
due to the algorithms involved in that step, (S
´
anchez-
´
Avila and S
´
anchez-Re
´
ıllo, 2002; de Santos-Sierra
et al., 2007).
The template is extracted by Z, using a circular
section (Fig. 1), averaging the intensities values along
the radius of the crown, ρ, for each angle of the pre-
vious section, α
i
, ∀i ∈ N ∩ [0, 255], (de Santos-Sierra
et al., 2007).
The circular section provides a template of 256
points, where each point is represented by a double
precision value in [0, 255], due to the grayscale repre-
sentation of the iris image. By the use of a 256
o
circu-
lar section, eyelids are avoided, although a 360
o
sec-
tion can be considered when suitable, regarding eye
aperture, (de Santos-Sierra et al., 2007).
SYNTHETIC IRIS IMAGES FROM IRIS PATTERNS BY MEANS OF EVOLUTIONARY STRATEGIES - How to
Deceive a Biometric System based on Iris Recognition
195

Figure 1: Region of Interest in Feature Extraction.
2.3 From Original to Synthetic
Once the template extraction has been presented, the
reader could realize that not the whole image is con-
sidered as a part of the template, but only many pixels.
In fact, those pixels are included in the previous circu-
lar section. Furthermore, a certain image I is consid-
ered as a base image, from which the algorithms will
be able to evolve a fake image. This must be done, if
a close-human fake is required. It is far easier to fake
several points in an image than the whole image.
According to these previous statements, several
definitions must be considered, before starting with
the explanation of the approaches. First of all, the im-
age I is randomly selected. From now, I will be con-
sidered as a matrix, where X and Y represent the sets
for horizontal and vertical coordinates respectively,
assuming that a pixel of I is represented by its position
within the image, (x, y) ∈ X × Y , and its color inten-
sity, I(x, y) ∈ N ∩ [0, 255], (Gonz
´
alez et al., 2004).
Let V be the matrix containing all the intensity
values within previous circular section. Matrix V has
256 columns and ρ rows, where ρ is the previous cir-
cular section width. Therefore, Ξ ⊂ X and ϒ ⊂ Y are
defined as those positions, in terms of X and Y , whose
pixels are contained in V . In other words, Ξ and ϒ are
the matricial representation of previous circular sec-
tion.
Matrix V is calculated once for image I, since V
gathers the unique values to be modified to fake im-
age I. When image I is presented to the system, fea-
ture extraction step will come up with a template read
from those pixels located in Ξ and ϒ, the rest of I is
neglected for template extraction.
In fact, template T associated with image I can be
obtained as:
T ( j) =
∑
i
V (i, j)
ρ
(4)
Once the nomenclature is stated, the two ap-
proaches are presented. First approach regards evo-
lutionary algorithms, (Michalewicz, 1996), finding
optimal solution by evolving those pixels contained
in V . On the other hand, second approach contem-
plates the possibility of changing the order in Ξ and
ϒ, in other words, changing the position of each pixel,
but not altering its intensity. Both approaches entail
evolutionary strategies, but with different approaches.
The performance of both will be presented in section
3.
2.3.1 Evolutionary Strategies on V
An evolutionary algorithm is a suitable manner of
tackling minimization and maximization problems,
(Michalewicz, 1996; Eiben and Smith, 2003). How-
ever, the problem must be adapted to make it suit-
able for evolutionary strategies. Since each template
T ∈ T verifies to be a 256 components vector, the
strategy involves dividing the problem into 256 in-
dependent problems. The j-component of T corre-
sponds to the average of the components in column j
from matrix V , being the representation for the sub-
problem j a vector called v
j
=< a
1, j
, a
2, j
, . . . , a
ρ, j
>
with ρ components and a
i, j
∈ V where i ∈ {1,. . . , ρ}
and j ∈ {1, . . . , 256}.
The procedure deployed under this section con-
templates several steps before meeting the goal of ob-
taining an optimal solution:
• Fitness Function: This function provides the al-
gorithm with a Termination Condition. The evo-
lutionary algorithm will seek the solution until a
certain value of fitness function is achieved. An
appropriate fitness function is as follows in Eq. 5.
|T ( j) − ¯v
j
| =
T ( j) −
∑
ρ
i=1
a
i
ρ
(5)
This fitness function must be minimized until a
certain extent η
0
according to previous problem
statement. This function exists for each subpro-
blem.
• Population and Initialization: The population of
each subproblem consists of 50 members, each of
them different to each other, in order to ensure di-
versity property, (Eiben and Smith, 2003). Each
member of the population is created based on a
uniform distribution. Such a distribution is uni-
form in the set formed by minimum and maxi-
mum value of column j for each j-subproblem.
BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing
196

For each subproblem, 50 members of the popu-
lation (vectors) are created. The reason why this
initialization is performed is due to the fact that
they present a previous solution quite close to the
final result which still remains unknown.
• Parent Selection: Parent Selection will provide
those individuals in the population most suitable
to mate, without neglecting the fact that less suit-
able individuals should be also considered as pos-
sible parents to create next offspring.
Thus, every individual is selected based on:
ξ
j
= |T ( j) − ¯v
j
|
which indicates to what extend the results dif-
fers from aim. According to ξ
j
, those individuals
more capable (with ξ
j
→ 0) are more likely to be
selected than those whose ξ
j
is far from 0. In the
literature, (Eiben and Smith, 2003), the Parent Se-
lection described within this document is similar
to Fitness Proportional Selection.
• Recombination: Having parents selected, a new
offspring emerges as a result of mating previous
parents. However, a recombination must be done
in order to provide more richness to such off-
spring. The algorithm proposed in this approach
is known as Whole Arithmetic Recombination,
(Eiben and Smith, 2003), with its parameters set
to α = 0.3, accordingly to (Eiben and Smith,
2003; Back et al., 2000a; Back et al., 2000b),
where 0 < α < 1 is suggested. On the other hand,
a Uniform Crossover operator is proposed to carry
out such an operation with a p
c
= 0.7 probability.
Lower values may make the algorithm not to con-
verge in a reasonable time, (Back et al., 2000a;
Back et al., 2000b).
• Mutation: Mutation is an operator capable of
modifying the offspring by changing several el-
ements in the alleles (individuals). For the sake of
an optimal solution, mutation must always be car-
ried out, but with lower probability than Recom-
bination. In this work, mutation probability was
experimentally set to p
m
= 0.25. Higher values
of p
m
make the algorithm not to converge, (Eiben
and Smith, 2003; Back et al., 2000a; Back et al.,
2000b).
• Survivor Selection Mechanism: This mechanism
is responsible for managing the process whereby
the population of parents (µ) and the new off-
spring (λ) is reduced to the size of popula-
tion. Concretely, this approach considers Elitism,
(Eiben and Smith, 2003), as the most suitable
mechanism for survivor selection, since it com-
bines Age-based replacement and Fitness-based
Replacement, in the same way parent selection is
carried out.
Finally, the algorithm under this approach will be
indicated as A
V
, as it is based on V matrix. The per-
formance of this algorithm will be considered in sec-
tion 3.
2.3.2 Evolutionary Strategies on Ξ and ϒ
This approach, namely A
Ξ,ϒ
, despite of being differ-
ent from previous algorithm, attempts the same aim.
Nonetheless, this approach intends to fake the iris, by
rotating rows in matrix V . In other words, this proce-
dure attempts to find the right combination for what a
solution is found in terms of problem statement.
Matrix V has ρ columns and 256 rows and is mod-
ified in column directions. In fact, the algorithm A is
conceived in this approach as an operator responsi-
ble for shifting the columns of V , so that the template
T changes as the evolutionary strategies attempts to
find the optimal solution. The operator able to carry
out every shift is called σ
m
i
with i = {1, . . . , nPop} and
m = {1,. . . , ρ}, where nPop is the number of individ-
uals in the population of the evolutionary algorithm.
This value will be set to nPop = 1000, according to
(Eiben and Smith, 2003; Back et al., 2000a; Back
et al., 2000b).
Despite of considering only shifts in row direc-
tion, there exist the possibility of also shifting in col-
umn directions. The operator responsible for this
strategy is defined as α
m
j
with j = {1, . . . , 256} and
m = {1, . . . , ρ}. Although possible, the implementa-
tion of an evolutionary algorithm considering both σ
m
i
and α
m
j
involves a non-acceptable processing time and
the results compared to an approach using only σ op-
erator, does not differ significatively. Thus, σ
m
i
opera-
tor is considered, but α
m
j
operator is ignored, although
its integration remains as future work.
The description of this approach follows in the
same manner as previous algorithm was described.
Most of the concepts coincide with those above in
section 2.3.1, since most representation has been con-
served, for the sake of simplicity regarding implemen-
tation.
• Fitness Function: Same function as in previous
section is selected. However, several considera-
tions must be taken into account. For instance,
threshold η
0
cannot be assured to be achieved, but
minimum of fitness function can be obtained, al-
though the performance of the whole algorithm
could not be so promising as previous approach.
Note the constraints of this algorithm are more
restrictive than before, being on the contrary less
complex in terms of processing time. Thus, same
SYNTHETIC IRIS IMAGES FROM IRIS PATTERNS BY MEANS OF EVOLUTIONARY STRATEGIES - How to
Deceive a Biometric System based on Iris Recognition
197

1 2
3
ρ
1
2
3
256
1
1000
Figure 2: Population structure for A
Ξ,ϒ
.
function is considered as in Eq. (5) but searching
the minimum, and not a defined threshold η
0
.
• Population and Initialization: In this case, 1000
individuals for each population is selected, since
a wider population is require due to the simpli-
city of the operator σ
m
i
, (Eiben and Smith, 2003).
Each individual represent a V matrix, where the
operator σ
m
i
has been carried out. Fig. 2 intends
to clarify the structure of the population and pro-
vides a visual idea about the population. However,
σ
m
i
is the actual operator to be evolved, although
it is easier to think on the problem in terms of ma-
trices Ξ and ϒ.
• Parent Selection: Since this approach slightly dif-
fers from previous approach in the fact that what
is evolved is not the data, but the operators σ
m
i
,
parents must be selected based on those displace-
ments which provide a ξ
j
(as defined in Eq. (4))
close to zero.
• Recombination and Mutation: Both steps have
been gathered under this section. The operators
evolved are σ
m
i
and thus, the operators used be-
fore lack of any meaning in this section. Instead,
permutation operators are involved. More in de-
tail, Partially Mapped Crossover was carried out
for recombination with a probability of p
c
= .7,
and Swap Mutation was considered as a suitable
operator for Mutation, carried out with a proba-
bility of p
m
= .25, (Eiben and Smith, 2003; Back
et al., 2000a; Back et al., 2000b). These previous
values were set according to experimental results,
lower values for p
c
and higher values for p
m
made
the algorithm not converge.
• Survivor Selection Mechanism: As previously
stated, Elitism is selected as the most suitable so-
lution, based on experimental results.
3 RESULTS
Considering the aim of these algorithms, a function
is required to measure how similar an original and a
fake are. Many different proposals exist in literature,
(Gonz
´
alez et al., 2004), in order to assess how dif-
ferent two signals are. The selected function, namely
ε, provide with a fast and accurate manner of meet-
ing this goal, and coincides with fitness function in its
definition. Given two functions, f and g, ε is defined
as follows:
ε =
Z
| f − g| (6)
Notice that this function is the simplest measure-
ment function. Main reason to use this function re-
gards the fact that if with the simplest function the
results are promising and acceptable, (see section 3),
more complicated measurement functions will pro-
vide more thorough and precise results. Nonetheless,
an implementation with more complex functions re-
mains as future work.
Once evaluation function is defined, an experi-
ment comparing deviation in terms of ε was car-
ried out among different samples of same individu-
als, and different samples of their corresponding syn-
thetic copies. Next picture highlights the results ob-
tained in these experiments: horizontal lines indicate
the average (µ
Orig
,
) and standard deviation range
(σ
Orig
, ) of ε among real samples of a same in-
dividual. On the other hand, dotted lines ( and
) indicate the performance of the algorithms A
V
and A
Ξ,ϒ
respectively. Notice how horizontal lines
split the space in three different regions: a region
where falsifications are more similar to original than
real samples of the same user from which original
was taken (‘Best’); a region where fake is similar to
real samples (‘Good’) and a region where falsifica-
tions could not deceive the system (‘Bad’).
Since both implementations of the algorithm, A
V
and A
Ξ,ϒ
, depends on η, several performance of both
implementations were carried out for each value of η,
(Fig. 3). However, notice that although A
Ξ,ϒ
depends
on η, its aim attempts to achieve the closest minimum
to η
0
, which might not coincide with η
0
.
Several conclusions can be extracted from Fig. 3.
First of all, A
V
and A
Ξ,ϒ
come out with solutions
more similar to their respective originals (from which
they were copied) than even those samples taken from
the same individual from which original images were
taken. In other words, depending on η, falsifications
can be ‘Good’ if ε is in the deviation interval among
real samples, better if ε is under that range, or ‘Bad’
otherwise. In this former case, the result provided by
A
V
and A
Ξ,ϒ
is not considered as a valid solution.
BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing
198
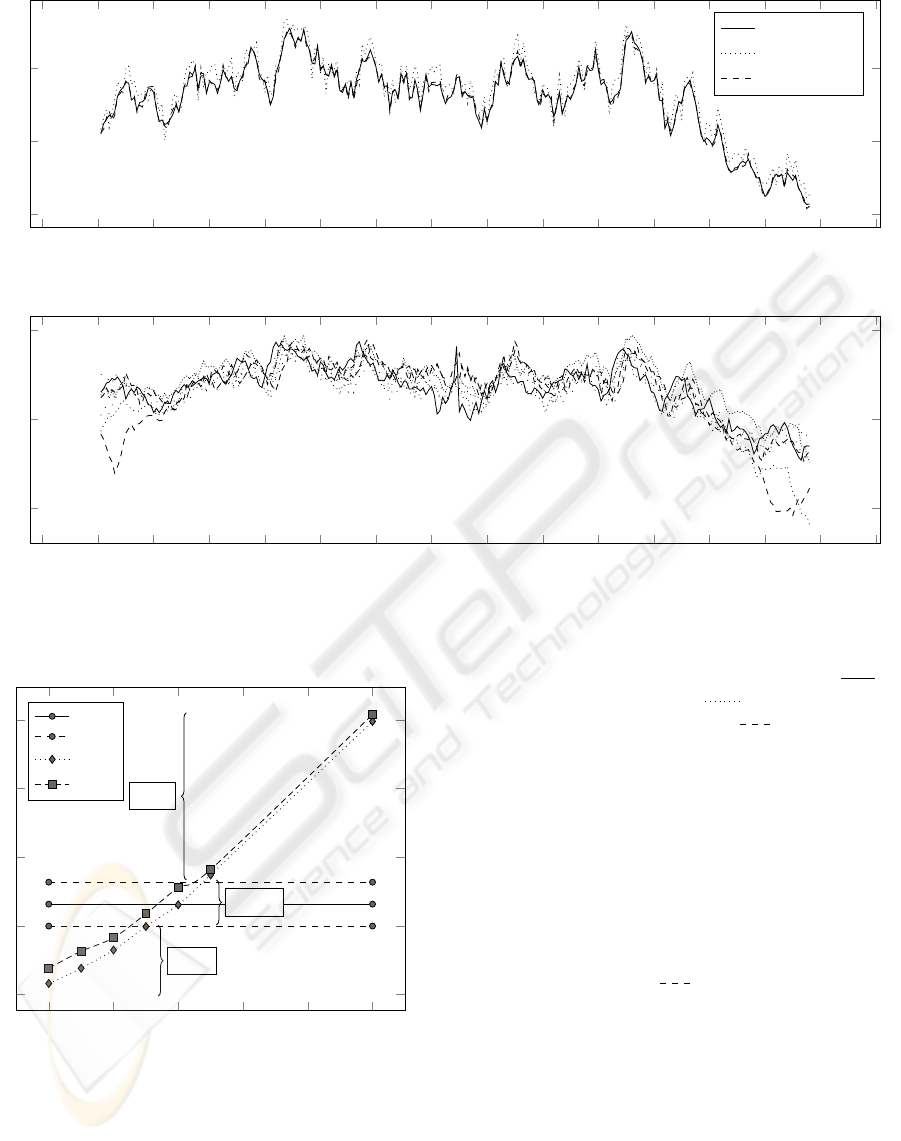
−20 0 20 40
60
80 100 120 140
160
180 200 220 240
260
280
130
140
150
Original
A
Ξ,ϒ
, η = 0
A
V
, η = 0
Figure 4: Result of both approaches, A
V
and A
Ξ,ϒ
, compared to the original pattern.
−20 0 20 40
60
80 100 120 140
160
180 200 220 240
260
280
120
140
160
Figure 5: Patterns from different samples belonging to the same user.
0 2 4
6
8 10
0
2
4
6
8
η
η(η)
µ
Orig
σ
Orig
A
V
A
Ξ,ϒ
Good
Best
Bad
Figure 3: Comparison between A
V
, A
Ξ,ϒ
and original sam-
ples in terms of η.
The performance of A
V
and A
Ξ,ϒ
is presented in
Fig. 4. Notice that A
V
is almost equal to the ori-
ginal, and therefore, some difficulties can arise when
trying to distinguish Original from A
V
in Fig. 4. A vi-
sual evaluation of the performance of both algorithms
can be seen in Fig. 8 and in Fig. 9, where ( )
represents an original pattern, ( ) represents a per-
formance of A
Ξ,ϒ
with η = 0 and ( ) represents a
performance of A
V
with η = 0. The performance of
A
V
is in general better than A
Ξ,ϒ
due to its own defi-
nition, however both provide optimal solutions when
compared to real data from same individuals.
This statement can be assessed in Fig. 5, where
patterns of the same user are depicted. Notice how
different are two samples from the same user. In fact,
that difference is far more noticeable among original
samples belonging to the same user, than among fal-
sification of a certain original sample. Furthermore,
the fake provided by A
V
( ) is extremely similar to
original.
Together with these previous visual patterns, and
important question comes up: How does a fake iris
image look like? Obviously, reader must notice that
a considerable amount of pixel within the image have
been altered, so that the image may look strange to
a human. However, that appearance lacks of mean-
ing for a computer, since the system extracts only that
region suitable for a posterior pattern extraction, ig-
noring how ‘human’ the iris looks like.
Thus, although an altered image by these former
SYNTHETIC IRIS IMAGES FROM IRIS PATTERNS BY MEANS OF EVOLUTIONARY STRATEGIES - How to
Deceive a Biometric System based on Iris Recognition
199
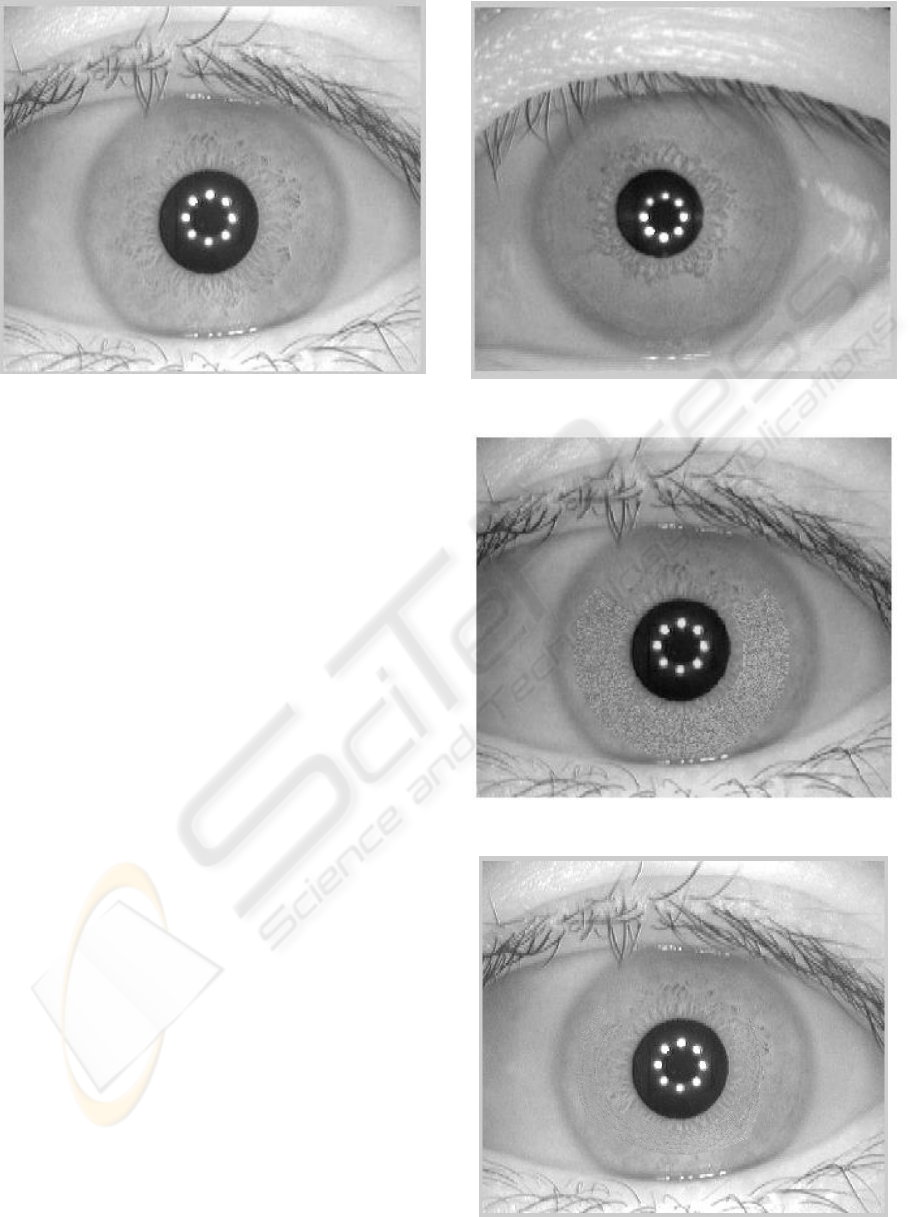
Figure 6: Image where falsification will take place.
methods could seem weird at first sight, it is totally ac-
cepted by the computer. In the end, the computer will
be responsible of processing the image, not the hu-
man. Actually, providing the synthetic image with a
more human-like appearance remains as future work.
However, the main difference between A
V
and
A
Ξ,ϒ
consists of the fact that A
V
achieves more pre-
cise results and can obtain a solution closer to the tar-
get, but on the contrary, the visual aspect of a fake
image is far from being real, in other words, it is ob-
vious that the image has been altered. On the other
hand, A
Ξ,ϒ
achieves worst results and is more time-
consuming. However, the visual aspect provided by
this latter approach (A
Ξ,ϒ
) does not look very differ-
ent from a human iris, and in fact, this difference is
negligible.
Fig. 6 shows the image used to make falsifica-
tion. This image is chosen randomly, and the algo-
rithm does not depend on this previous image selec-
tion. Moreover, Fig. 7 provides the image to fake. In
other words, the idea is to enter the system where Fig.
7 is registered, using Fig. 6.
The results of the algorithms are shown in Fig. 8
and in Fig. 9, which represent the performance of A
V
and A
Ξ,ϒ
respectively. Notice how the appearance of
Fig. 8 is slightly different from a human iris, and how
Fig. 9 almost does not differ from Fig. 6. It must
be emphasized the fact that although visually they do
not look ‘standard’ human iris, the system makes no
difference. Furthermore, achieving a more human ap-
pearance in both performance remains as future work.
Figure 7: Image whose template is T
RU
.
Figure 8: Visual result of A
V
.
Figure 9: Visual result of A
Ξ,ϒ
.
BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing
200

4 CONCLUSIONS
This article presents two approaches for biometric
synthesis. Both provide an accurate performance
when creating a fake copy from an original pattern,
although both compromise accuracy, time and human
appearance. Main conclusion highlights the fact that
copies are better than original samples.
Use cases inferred from synthetic biometric data
regard biometric data reconstruction, synthetic data
for testing biometric systems, or tightening up bio-
metric security.
Regarding future work, stricter constraints will
lead to a more human-like appearance in final syn-
thetic image, focusing on the texture. Furthermore,
tests will be carried out in more databases apart from
CASIA v3, once the algorithm is able to deal with
more complex textures. Despite of being far be-
yond the scope of this article, time performance must
be considered for a real time application. However,
reader must notice that time is not a constraint when
doing ‘hacking’ activities.
One more aspect regards performance of
the whole biometric system when identify-
ing/authenticating a certain individual. No efforts
have been done focusing on this aspect, since
synthetic copies are so similar to originals, that the
performance of the biometric system will be obvi-
ously decreased if these images are included within
the database. However, to what extent a biometric
system loses accuracy with these images remains as
future work.
Finally, a more complex algorithm, merged as a
result of both approaches, will be considered as a
more precise and promising procedure, gathering best
characteristics of each algorithm, including also α
m
j
operator as described before, (Gonz
´
alez et al., 2004).
REFERENCES
Back, T., Fogel, D. B., and Michalewicz, Z. (2000a). Evo-
lutionary Computation 1: Basic Algorithms and Op-
erators. Taylor & Francis, Bristol, 1
st
edition.
Back, T., Fogel, D. B., and Michalewicz, Z. (2000b). Evo-
lutionary Computation 2: Advanced Algorithms and
Operators. Taylor & Francis, Bristol, 1
st
edition.
Boles, W. and Boashash, B. (1998). A human identification
technique using images of the iris and wavelet trans-
form. In IEEE Trans. Signal Processing, volume 46,
page 11851188.
Capelli, R., Lumini, A., Maio, D., and Maltoni, D. (2006).
Can fingerprints be reconstructed from iso templates?
In Proc. International Conference on Control, Au-
tomation, Robotics and Vision (ICARCV2006).
Chun, C. N. and Chung, R. (2004). Iris recognition for
palm-top application. In International Conference on
Biometric Authentication (ICBA 2004), volume 3072,
pages 426–433. Springer-Verlag.
Cook, P. R. (2002). Real Sound Synthesis for Interactive
Applications. AK. Peters, 1
st
edition.
Cui, J., Wang, Y., Huang, J., Tan, T., Sun, Z., and Ma, L.
(2004). An iris image synthesis method based on pca
and super-resolution. In Proc. Int. Conf. on Pattern
Recognition.
Daugman, J. (1993). High confidence visual recognition
of persons by a test of statistical independence. In
IEEE Transactions on Pattern Analysis and Machine
Intelligence, volume 15.
Daugman, J. (2004). How iris recognition works. In IEEE
Transactions on Circuits and Systems For Video Tech-
nology, volume 14.
de Santos-Sierra, A., S
´
anchez-
´
Avila, C., and S
´
anchez-
Re
´
ıllo, R. (2007). Sistema de identificaci
´
on
biom
´
etrica mediante patr
´
on de iris utilizando op-
eradores morfol
´
ogicos y representaci
´
on. In Con-
greso Iberoamericano de Seguridad Inform
´
atica
(CIBSI2007), pages 427–434.
Eiben, A. E. and Smith, J. E. (2003). Introduction to Evolu-
tionary Computing. Springer, Berlin.
Gonz
´
alez, R. C., Woods, R. E., and Eddins, S. L. (2004).
Digital Image Processing. Prentice All, 2
nd
edition.
Guyon, I. (1996). Handwriting synthesis from handwritten
glyphs. In Proc. 5th Int. Workshop on Frontiers of
Handwriting Recognition, page 309312.
Michalewicz, Z. (1996). Genetic Algorithms + Data Struc-
tures = Evolutionary Programs. Springer, Berlin, 3
rd
edition.
S
´
anchez-
´
Avila, C. and S
´
anchez-Re
´
ıllo, R. (2002). Iris-
based biometric recognition using dyadic wavelet
transform. In IEEE Aerospace and Electronic Systems
Magazine, pages 3–6.
Schwefel, H. P. (1995). Evolution and Optimum Seeking.
Wiley, New York.
Yanushkevich, S. N. (2006). Synthetic biometrics: A sur-
vey. In International Joint Conference on Nueral Net-
works, pages 676–683.
Yanushkevich, S. N., Wang, P. S. P., and Gavrilova, M. L.
(2007). Image Pattern Recognition: Synthesis and
Analysis in Biometrics. Imperial College Press.
SYNTHETIC IRIS IMAGES FROM IRIS PATTERNS BY MEANS OF EVOLUTIONARY STRATEGIES - How to
Deceive a Biometric System based on Iris Recognition
201
