RATIO-HYPOTHESIS-BASED FUZZY FUSION WITH

APPLICATION TO CLASSIFICATION OF CELLULAR

MORPHOLOGIES

Tuan D. Pham

School of Engineering and Information Technology, University of New South Wales, Canberra, ACT 2600, Australia

Xiaobo Zhou

Center for Biotechnology and Informatics, Methodist Hospital Research Institute, Houston, TX 77030, U.S.A.

Keywords:

Permanence of ratio, Information fusion, Pattern classiﬁcation, Cellular phenotypes, Bio-imaging.

Abstract:

Fusion of knowledge from multiple sources for pattern recognition has been an active area of research in

many scientiﬁc disciplines. This paper presents a fuzzy version of a probabilistic fusion scheme, known

as permanence-of-ratio-based combination, with application to analysis of cellular imaging for high-content

screening. Classiﬁcation of cellular phenotypes has been carried out to illustrate the usefulness of the

permanence-of-ratio-based fuzzy fusion.

1 INTRODUCTION

Information or data fusion can be deﬁned as the use of

mathematical methods that combine data from multi-

ple sources to obtain the resultant knowledge in or-

der to achieve inferences, which will be more efﬁ-

cient and potentially more accurate than if they were

achieved by means of considering separate single

sources. Information fusion can be performed on a

low-level or high-level process depending on the pro-

cessing stage at which fusion takes place. Low-level

fusion combines several sources of raw data to pro-

duce new raw data (Pellizzeri et al., 2002). The ex-

pectation is that fused data is more informative and

synthetic than the original raw data. High-level fusion

typically combines features from multiple classiﬁers,

or signals from multiple sensors for logical decision

making (Muller et al., 2001; Das, 2008).

There are many mathematical operators developed

for data fusion such as the averaging rule, multiplica-

tion rule, probabilistic models, mathematical theory

of evidence, machine learning methods, and fuzzy in-

tegral (Chi et al., 1996). For high-level fusion, the ra-

tionale of combining knowledge from various sources

is that it is always difﬁcult or impossible to design

a single classiﬁer or to use a single feature for pat-

tern classiﬁcation to achieve the best results, because

a particular classiﬁer or feature can only be robust for

handling a particular identity of an object, which may

vary under different settings. Furthermore, different

problems may require different data fusion methods

to obtain effective solutions depending on the types

of features.

This paper discusses the use of fuzzy measures for

combining evidences from multiple sources, where

the strong assumption of data independence is relaxed

(Journel, 2002). The utilization of such novel idea ap-

pears to be promising for pattern classiﬁcation but it is

still rarely explored in the new ﬁeld of bioinformatics.

We are interested in applying an information fusion

scheme for combining output from multiple classi-

ﬁers in order to improvethe results for classifying var-

ious cellular phenotypes for robust automated analy-

sis of genome-wide high-content screening of ﬂuores-

cent microscopy images of cells.

The rest of this paper is organized as follows. Sec-

tion 2 introduces the concept of the permanence of

ratio hypothesis for knowledge combination. Sec-

tion 3 proposes a ratio-hypothesis-based fuzzy fusion

scheme. Section 4 illustrates the application of the

proposed fusion model for classifying cellular pheno-

types for genome-wide screening, such screening is

essential to the rapid discovery of basic biological cell

principles such as control of cell cycle and cell mor-

202

D. Pham T. and Zhou X. (2010).

RATIO-HYPOTHESIS-BASED FUZZY FUSIONWITH APPLICATION TO CLASSIFICATION OF CELLULAR MORPHOLOGIES.

In Proceedings of the Third International Conference on Bio-inspired Systems and Signal Processing, pages 202-207

DOI: 10.5220/0002707902020207

 SciTePress

phology. Section 5 presents the use of a Gaussian dis-

tribution for estimating fuzzy densities. Finally, the

conclusion of the ﬁnding is given in Section 6.

2 INFORMATION FUSION USING

PERMANENCE OF RATIO

HYPOTHESIS

Based on the engineering paradigm of the perma-

nence of updating ratios, which asserts that the rates

or ratios of increments are more stable than the incre-

ments themselves, as an alternative to the assumption

of the full or conditional independence of probabilis-

tic models; Journel introduced a scheme for informa-

tion fusion of diverse sources (Journel, 2002). This

scheme allows the combination of data events without

having to assume their independence. This informa-

tion fusion is described as follows.

Let P(A) be the prior probability of the occurrence

of data event A; P(A|B) and P(A|C) be the probabil-

ities of occurrence of event A given the knowledge

of events B and C, respectively; P(B|A) and P(C|A)

the probabilities of observing events B and C given A,

respectively. Using Bayes’ law, the posterior proba-

bility of A given B and C is

P(A|B,C) =

P(A,B,C)

P(B,C)

P(A)P(B|A)P(C|A,B)

P(B,C)

(1)

The simplest way for computing the two proba-

bilistic models is to assume the model independence,

giving P(C|A, B) = P(C|A), and P(B,C) = P(B)P(C).

Thus, (1) can be rewritten as

P(A|B,C)

P(A)

P(A|B)

P(A)

P(A|C)

P(A)

(2)

However, the assumption of conditional indepen-

dence between the data events usually does not statis-

tically perform well and leads to inconsistencies in

many real applications (Journel, 2002). Therefore,

an alternative to the hypothesis of conventional data

event independence should be considered. The per-

manence of ratios based approach allows data events

B and C to be incrementally conditionally dependent

and its fusion scheme gives

P(A|B,C) =

1+ x

a+ bc

∈ [0,1] (3)

where

a =

1− P(A)

P(A)

, b =

1− P(A|B)

P(A|B)

c =

1− P(A|C)

P(A|C)

, x =

1− P(A|B,C)

P(A|B,C)

An interpretation of the fusion expressed in (3) is

as follows. Let A is the target event which is to be up-

dated by events B and C. The term a is considered as

a measure of prior uncertainty about the target event

A or a distance to the occurrence of A without any up-

dated evidence. We have a = 0 for P(A) = 1 if target

event A is certain to occur; and a = 0 for P(A) = 0 if A

is an impossible event. Likewise, b and c measure the

distances to A knowing about its occurrence after ob-

serving evidences given by B andC, respectively. The

term x is the distance to the target event A occurring

after observing evidences given by both events B and

C. The ratio c/a is then the incremental (increasing

or decreasing) information of C to that distance start-

ing from the prior distance a. Similarly, the ration x/b

is the incremental information of C starting from the

distance b. Thus, the permanence of ratios provides

the following relation

≈

(4)

which says that the incremental information about C

to the knowledge of A is the same after or before

knowing B. In other words, the incremental contri-

bution of information from C about A is independent

of B. This expression relaxes the restriction of the as-

sumption of full independence of B and C.

For the generation of k data eventsE

, j = 1,...,k;

the conditional probability provided by a succession

of (k− 1) permanence of ratios is given as

P(A|E

, j = 1,...,k) =

1+ x

∈ [0, 1] (5)

where

x =

∏

j=1

k−1

≥ 0

a =

1− P(A)

P(A)

1− P(A|E

)

P(A|E

)

, j = 1,...,k

It is clear that expression (5) requires only the

knowledge of the prior probability P(A), and the k

elementary single conditional probabilities P(A|E

j = 1,...,k, which can be independently computed.

We next present the concept of fuzzy measures

and how we can implement fuzzy measures into the

RATIO-HYPOTHESIS-BASED FUZZY FUSIONWITH APPLICATION TO CLASSIFICATION OF CELLULAR

MORPHOLOGIES

203

framework of permanence-of-ratio hypothesis for in-

formation fusion, where the independence of joint

events can be more relaxed to provide a better model

for information consistency.

3 RATIO-HYPOTHESIS-BASED

FUZZY INFORMATION

FUSION

Let X be a ﬁnite set X = {x

,...,x

}. A fuzzy

measure g deﬁned on X is a set function g : P (X) →

[0,1] satisfying the following axioms (Sugeno, 1977):

1. g(

0) = 0, and g(X) = 1.

2. If A ⊆ B, then g(A) ≤ g(B).

where P (X) denotes the power set of X.

It is noted that when the second property is not

satisﬁed, g is called a non-monotonic fuzzy measure

(Grabisch, 1996). There are 2

coefﬁcients being

equivalent to the cardinality of P (X) to compute a

fuzzy measure on X. These coefﬁcients are the values

of g for all subsets of X and they are not independent

since they must satisfy the property of monotonicity.

Theoretically, the concept of fuzzy measures is the

generalization of the classical measure theory which

is restrictive on the hypothesis of additivity; whereas

additivity is relaxed by the theory of fuzzy measures.

Sugeno (1977) deﬁned a fuzzy measure known as

the g

-fuzzy measure that satisﬁes the following ad-

ditional condition, ∀A,B ⊂ X, and A∩ B =

(A∪ B) = g

(A) + g

(B) + λg

(A)g

(B), λ > −1.

(6)

To simplify the notation, let g

= g({x

}) which is

called a fuzzy density function. A fuzzy density g

can be interpreted as the degree of belief or degree of

importance that the corresponding attribute x

makes

an effect or contribution towards the whole fuzzy sys-

tem when all attributes are considered together. Let

A = {x

,...,x

} ⊂ X, g

(A), λ 6= 0, can be ex-

pressed as(Lesczynski et al., 1985)

(A) =

∏

∈A

(1+ λg

) − 1

(7)

The value of λ can be calculated using the condi-

tion g(X) = 1 as follows.

λ+ 1 =

∏

i=1

(1+ λg

) (8)

The following properties of the g

-fuzzy measure

will be helpful in the computation of the parameter λ

(Tahani and Keller, 1990).

1. Lemma: For a ﬁnite set {g

}, 0 < g

< 1, there

exists a unique root λ ∈ (−1,+∞), and λ 6= 0.

Based on this lemma, λ can be determined by

solving (n − 1) degree polynomial and selecting

the unique root > −1.

2. If

∑

i=1

< 1, then λ > 0.

3. If

∑

i=1

> 1, then −1 ≤ λ < 0.

Among other computer methods being useful for

clinical applications such as Mycine (Shortlie, 1976)

and several other medical expert systems (Berner,

1998), the Shafer’s theory of evidence (Shafer, 1976)

is a popular tool for medical decision making (Klir

and Wierman, 1999). There are some connections

between the belief and plausibility measures of the

theory of evidence and the Sugeno’s fuzzy measures.

The function which maps P (X) to [0, 1] is called a

belief function, denoted as bel, iff it satisﬁes the fol-

lowing conditions (Shafer, 1976):

1. bel(

0) = 0, bel(X) = 1

2. bel(

) ≥

∑

06=I⊆{x

,...,x

}

(−1)

|I|+1

bel(

)

The plausibility measure is deﬁned in terms of the

belief measure as

pl(A) = 1− bel(

A) (9)

Some other mathematical relationships between

belief and plausibility measures, ∀A ∈ P (X), are

bel(A) + bel(

A) ≤ 1, pl(A) + pl(

A) ≥ 1

and

pl(A) ≥ bel(A)

Based on the deﬁnitions and properties of the

belief and plausibility measures, Banon (1981) has

shown that a g

-fuzzy measure is a belief measure

when λ ≥ 0, and a g

-fuzzy measure is a plausibil-

ity measure when λ ≤ 0.

By allowing the calculation of the joint fuzzy

events g(A|B,C) which makes the terms b and c de-

ﬁned in (5) equal to each other, we can equivalently

deﬁne a fuzzy probabilistic fusion operator, denoted

as F , for a target event A which is to be updated by

events B and C, as

F (A|B,C) =

a+ f

(10)

where

BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing

204

a =

1− g(A)

g(A)

, and f =

1− g(A|B,C)

g(A|B,C)

The general form for the ratio-hypothesis-based

fuzzy fusion can be deﬁned by generalizing (10) to

account for the fuzzy measure of k events E

, j =

1,...,k, giving

F (A|E

, j = 1,...,k) =

a+ x

∈ [0,1] (11)

where

x =

1− g(A|E

,...,E

)

g(A|E

,...,E

)

Based on both (10) and (11), the ratio-hypothesis-

based fuzzy fusion of multiple events allows a

stronger conditional dependence than the ratio-

hypothesis-based fusion expressed in (3) and (5) but

still only requires the knowledge of the fuzzy densi-

ties of the multiple events. We next discuss how to

estimate the fuzzy densities using the Gaussian prob-

ability function and also present the Bayes classiﬁer.

4 BAYES CLASSIFIER AND

ESTIMATING FUZZY

DENSITIES BY GAUSSIAN

FUNCTION

Pattern recognition using decision-theoretic frame-

work is based on a discriminant or decision function

to assign the unknown pattern to the best match. Let

x = (x

,...,x

)

be an n-dimensional feature vec-

tor; and Ω = {ω

,ω

,...,ω

} the set of m distinct

patterns. The Bayes classiﬁer for a 0-1 loss function

is expressed as (Gonzalez and Woods, 2002)

(x) = p(x|ω

)P(ω

); i = 1,...,m. (12)

where d

(x) is a decision function that measures how

likely the unknown pattern x belongs to the ith pat-

tern class, p(x|ω

) is the probability density function

of the feature vector of class ω

, and P(ω

) is the prob-

ability that class ω

occurs.

The recognition procedure is to compute the m de-

cision function d

(x), i = 1,...,m; and then assign the

pattern to the class whose decision function value is

maximum. Using the Gaussian probability distribu-

tion function, its n-dimensional form is given as

p(x|ω

) =

(2π)

n/2

(detC

)

1/2

−

[(x−m

)

−1

(x−m

)]

(13)

where C

and m

are the covariance matrix and mean

vector of the pattern feature of class ω

, and detC

is the determinant of C

. Expression (13) is used to

determine the fuzzy density for each test sample that

will be discussed in the next section

Using the monotonically increasing property of

the logarithm, the decision function d

(x) has the fol-

lowing logarithmic form

(x) = ln[p(x|ω

)P(ω

)] = ln p(x|ω

) + lnP(ω

)

(14)

The substitution of the expression for the Gaus-

sian probability distribution function expressed in

(13) into (14) and after some mathematical rearrange-

ment give

(x) = lnP(ω

) −

ln(detC

)

−

[(x− m

)

−1

(x− m

)] (15)

The equation expressed in (15) is known as the

Bayesian decision function for Gaussian pattern class

under the condition of a 0-1 loss function.

5 FUSION-BASED

CLASSIFICATION OF

CELLULAR MORPHOLOGIES

USING PHENOTYPE

FEATURES

Fluorescent microscopy images of cells stained to re-

veal complex cellular features, such as cytoarchitec-

ture, are considered to be high-content images due to

the large amount of information they contain. These

images reveal numerous biological readouts, includ-

ing cell size, cell viability, DNA content, cell cycle,

and cell morphology. A gene’s function can be as-

sessed by analyzing alterations in a biological process

caused by the absence of that gene. A speciﬁc study

concerns a cell-based assay for the activity of the Rho

GTPase Rac1 using the Drosophila Kc167 embryonic

cell line (Wang et al., 2008).

Distinct morphological changes in cells both in

vitro and in vivo caused by constitutively active forms

of Rho proteins can be observed. Kc167 cells are

small and uniformly round.

We used 643 normal, 321 rufﬂing, and 210 spiky

RNAi cell samples in this study. Using a feature ex-

traction procedure (Wang et al., 2008), 211 texture

and shape features for each cell image were obtained.

RATIO-HYPOTHESIS-BASED FUZZY FUSIONWITH APPLICATION TO CLASSIFICATION OF CELLULAR

MORPHOLOGIES

205

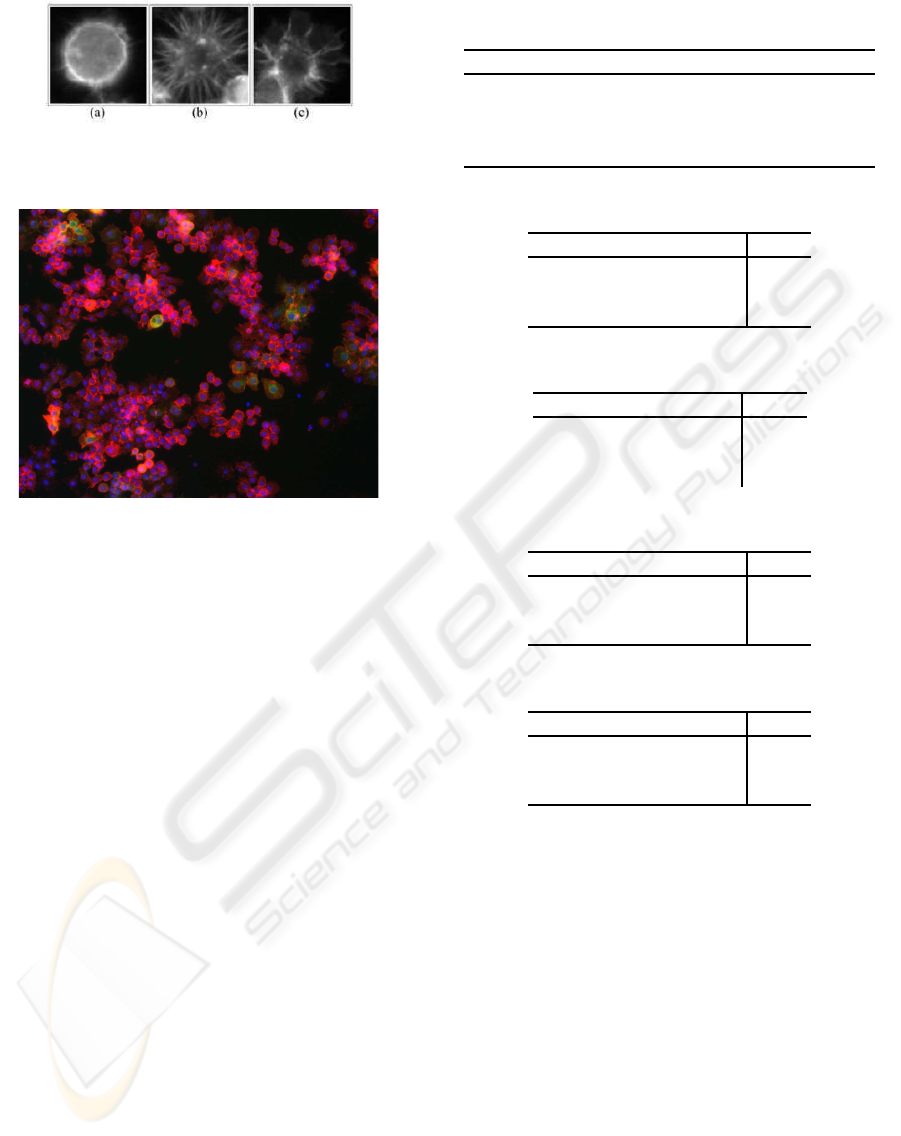
Figure 1: Three cellular phenotypes of Drosophila Kc167

cells: a) Normal; b) Spiky; c) Rufﬂing.

Figure 2: Typical screening image.

To test the performance of the proposed fuzzy infor-

mation fusion, we used only 2 sets of features, each

set consists of 12 different features of the 211 tex-

tures and shapes previously discussed. We used half

of the samples for data testing (320, 100, and 160

for class 1, class 2, and class 3; respectively) and the

other samples were used for training. Let A be a tar-

get class, and B and C the two different feature sets

used to identify A. For each set of features, expres-

sion (13) was used to compute p(x|ω

) for each sam-

ple x for class ω

, giving values for P(A|B) = g(A|B)

and P(A|C) = g(A|C) for each of the 3 classes (nor-

mal, spiky, and rufﬂing). Prior probabilities or fuzzy

densities for A for each of the 3 classes are assumed

to be equal, giving P(A) = g(A) = 1/3. We consider

that these sets of feature vectors do not completely

cover all possible features associated with the pheno-

types. Therefore, the subset φ was introduced to rep-

resent the set of all remaining possible features. The

fuzzy density of φ can be subjectively estimated. In

this study we set g({φ}) = 0.4 to represent the degree

of belief of the phenotype existence when all other

unforseen features are considered. It is noted that us-

ing different reasonable values of g({φ}) will not af-

fect the relative comparisons of the interactions of the

actual features. The Bayes classiﬁer was used to

classify the testing samples based on each of the two

feature sets. The two sets of output obtained from

the Bayes classiﬁer were then combined by the ratio-

based (probabilistic) fusion and the ratio-based fuzzy

Table 1: Correction rates (%) on classiﬁcation of cellular

phenotypes using different methods.

Class 1 2 3

Bayes classiﬁer 1 66.25 62.00 63.12

Bayes classiﬁer 2 64.06 64.00 61.25

Ratio-based fusion 76.88 65.00 65.00

Ratio-based fuzzy fusion 80.31 74.00 66.25

Table 2: Confusion matrix of Bayes classiﬁer 1.

Class 1 2 3 Total

1 212 39 69 320

2 18 62 20 100

3 27 32 101 160

Table 3: Confusion matrix of Bayes classiﬁer 2.

Class 1 2 3 Total

1 205 44 71 320

2 14 64 22 100

3 26 36 98 160

Table 4: Confusion matrix of probabilistic fusion.

Class 1 2 3 Total

1 246 25 49 320

2 16 65 19 100

3 24 32 104 160

Table 5: Confusion matrix of fuzzy fusion.

Class 1 2 3 Total

1 257 24 39 320

2 11 74 15 100

3 24 30 106 160

fusion operators.

The classiﬁcation rates obtained from Bayes clas-

siﬁer 1 (using feature set 1), Bayes classiﬁer 2 (using

feature set 2), probabilistic fusion, and fuzzy fusion

are given in Table 1. The confusion matrices (non-

diagonal elements indicate misclassiﬁed samples) of

the Bayes classiﬁer 1, Bayes classiﬁer 2, probabilis-

tic fusion, and fuzzy fusion are given in Tables 2-5,

respectively. The experimental results show that the

combined results are better than those obtained from

individual classiﬁers, and suggest the best perfor-

mance of the proposed fuzzy approach in all classes.

6 CONCLUSIONS

A proposed fusion scheme and its preliminary appli-

cation for classifying phenotypic classes of biologi-

BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing

206

cal cells have been discussed. The initial result for

validating the proof of concept of the model seems

to be promising for combining results from various

sources.

Extended investigation of the proposed approach

is under way to develop a key component for auto-

matic cellular phenotype identiﬁcation as an effort to-

ward the construction of a robust automated imaging

system for high-content genome-wide screening.

REFERENCES

Banon G. Distinction between several subsets of fuzzy mea-

sures, Fuzzy Sets and Systems 1981, 5: 291-305.

Berner ES, Ball MJ, Hannah KJ, Eds. Clinical Decision

Support Systems: Theory and Practice. New York:

Springer-Verlag, 1998.

Chi Z, Yan H, Pham, T. Fuzzy Algorithms: With Appli-

cations to Image Processing and Pattern Recognition.

Singapore: World Scientiﬁc, 1996.

Das S. High-Level Data Fusion. Norwood: Artech House,

2008.

Gonzalez RC, Woods RE. Digital Image Processing. NJ:

Prentice Hall, 2002.

Grabisch M. The representation of importance and interac-

tion of features by fuzzy measures, Pattern Recogni-

tion Letters 1996, 17: 567-575.

Journel AG. Combining knowledge from diverse sources:

An alternative to traditional data independence hy-

potheses, Mathematical Geology, 34 (2002) 573-595.

Klir GJ, Wierman MJ. Uncertainty-Based Information: El-

ements of Generalized Information Theory. Heidel-

berg: Physica-Verlag, 1999.

Lesczynski K, Penczek P, Grochulski PW. Sugeno’s fuzzy

measure and fuzzy clustering, Fuzzy Sets and Systems

1985, 15: 147-158.

Muller C, Rombaut M, Janier M. Dempster Shafer approach

for high level data fusion applied to the assessment

of myocardial viability, T. Katila et al. (Eds.): LNCS

2230, pp. 104-112, 2001.

Pellizzeri TM, Lombardo P, Oliver CJ. A new maximum

likelihood classiﬁcation technique for multitemporal

SAR and multiband optical images, Proc. IGARSS

2002, pp. 24-28

Shafer GA. A Mathematical Theory of Evidence. NJ:

Princeton University Press, 1976.

Shortliffe EH. Computer-based Medical Consultations:

Mycine. New York: Elsevier, 1976.

Sugeno M. Fuzzy measures and fuzzy integrals: A survey,

in: Fuzzy Automata and Decision Processes, Amster-

dam: Elsevier, pp. 89-102, 1977.

Tahani H, J. Keller J. Information fusion in computer vision

using the fuzzy integral, IEEE Trans. Systems, Man,

and Cybernetics 1990, 20: 733-741.

Wang J, Zhou X, Bradley PL, Chang SF, Perrimon N,

Wong STC. Cellular phenotype recognition for high-

content RNA interference genome-wide screening, J.

Biomolecular Screening 2008, 13: 29-39.

RATIO-HYPOTHESIS-BASED FUZZY FUSIONWITH APPLICATION TO CLASSIFICATION OF CELLULAR

MORPHOLOGIES

207