INFORMATION GAIN OF STRUCTURED MEDICAL

DIAGNOSTIC TESTS

Integration of Bayesian Networks and Ontologies

Marin Prcela, Dragan Gamberger, Tomislav Šmuc

Rudjer Boskovic Institute, Bijenicka 54, Croatia

Nikola Bogunović

Faculty of Electrical Engineering and Computing, University of Zagreb, Unska 3, Zagreb, Croatia

Keywords: Knowledge representation, Ontologies, Bayesian networks, Integration, Information gain, Decision support

system, Expert system.

Abstract: Usage of Bayesian networks in medical decision support system is in general case twofold: (1) for obtaining

probabilities of occurrence of medical events (i.e. possible diagnosis) and (2) for obtaining information gain

of actions that can be taken (i.e. diagnostic tests). On the other hand, typical role of ontology is to provide a

framework for definition of medical concepts, their structure and relations among them. In medical practice

diagnostic tests are commonly comprised of number of measurements or sub-tests – a structure which is

straightforwardly described by ontological language. In this paper we are analyzing the information gain of

such structured medical diagnostic tests. The purpose of this analysis is to allow finding (1) which

structured medical diagnostic test is at the given point the most informative one and (2) which elementary

measurements within a given diagnostic test are the most informative ones. Furthermore, we are analyzing

some computational issues which arise in the reasoning process.

1 INTRODUCTION

Bayesian networks (BN) have already demonstrated

their practical value in medical decision support

systems. The most exploited features of such system

are (1) finding probabilities of possible events in the

system (usually probabilities of diagnosis) and (2)

finding information gain (IG) of possible actions

that can be taken (usually medical diagnostic tests).

On the other hand, ontologies have become de facto

standard in medical decision support systems for

formalization of descriptive medical knowledge:

defining domain concepts and relations among them.

Medical domain is particularly suitable for usage

of IG as a decision support parameter. For example,

(Jagt 2002) uses BN to describe probabilistic

relations among medical concepts and uses IG to

find the most informative medical measurement

(test) considering possible final diagnoses (diseases).

In practice, medical diagnostic tests are commonly

comprised of more than one diagnostic parameters,

e.g. laboratory analysis of blood sample measures

levels of glucose, creatinine, cholesterol, urea, etc. It

would be useful to allow the decision support system

to perceive such structured medical test as a

conceptual unit. Still, one should be aware that it is

not necessary to measure all existing parameters

within test; one can choose which parameters are

currently interesting and disregard the others and

thus presumably cut the expenses of medical test and

save some time.

In this paper we are proposing approach which

uses BN for description of probabilistic relations

among medical concepts and measures IG of

composite medical diagnostic tests defined within

ontology. As we will demonstrate, the integration of

those two knowledge formalisms brings in some

additional features for the decision making but also

rises some computational issues in the reasoning

process.

It should also be noted that in medical practice

very often some other (non-medical) factors must be

taken into account: e.g. price of the test, availability

235

Prcela M., Gamberger D., Šmuc T. and Bogunovi

c N. (2010).

INFORMATION GAIN OF STRUCTURED MEDICAL DIAGNOSTIC TESTS - Integration of Bayesian Networks and Ontologies.

In Proceedings of the Third International Conference on Health Informatics, pages 235-240

DOI: 10.5220/0002713902350240

 SciTePress

of medical instruments, urgency, etc. Although

measure of IG does not take into account these

factors, it is possible to derive a weighted

combination (or some other type) of those factors to

form a comprehensive scale of medical test utility.

However this paper analyzes solely IG of actions in

pure medical sense.

The organization of paper is as follows. Chapter

2 previews the existing approaches for integration of

ontologies and BN. Chapter 3 demonstrates the

usage of BN in a medical decision support system.

Chapter 4 upgrades the described decision support

services with ontological knowledge and analyzes

means for performing reasoning tasks. Chapter 5

gives example of practical usage of such integrated

knowledge base in a single decision support system.

Chapter 6 discusses some performance issues of the

described approach related to reasoning phase.

2 RELATED WORK

Integration of ontologies with BN is not a new

paradigm. In (Pan 2005) BN is used to recognize

semantic relations between concepts in two different

ontologies, which enables automatic generation of

mappings between ontology concepts. Application

of this approach is described in the domain of

Semantic Web where problem of semantic relation

between ontologies is emphasized.

In (Devitt 2006) knowledge stored in the

ontology is used for generating possible structures of

BN. Since ontologies thoroughly define domain

concepts and existing relations among them there is

a possibility to use such knowledge to generate the

structure of BN. In (Town 2004) ontology is used

both to learn BN structure and in the process of

network training, i.e. learning probability tables of

network nodes. The usual process of BN training

(using existing data set) is augmented by scoring

scheme which is based on the ontological

knowledge.

In (McGarry 2007) high level knowledge

obtained from ontologies is integrated with newly

discovered knowledge extracted from BN which was

trained on existing data set. In (Huhns 2007)

ontology is used for management of evidence in the

BN. In (Wang 2008) ontology is used for integration

of heterogeneous data sources and BN is used for

making probabilistic suggestions.

In medical domain, (Jeon 2007) uses ontology

for semi-automatic construction of BN for

diagnosing diseases. In (Zheng 2005) guideline

modelling tool that uses ontological workflow

management (GLIF) is integrated with probabilities

obtained by BN.

As we have demonstrated in this brief overview,

previous attempts of integration of these knowledge

representation formalisms are focused mainly on

calculation of probabilities of outcomes of some

events. Methodology proposed in this paper is

focusing mainly towards the IG of possible actions.

This is the crucial difference of the proposed

methodology with already existing approaches of

integration of ontologies and BNs.

3 USING BAYESIAN NETWORK

It is possible to construct BN (1) manually by

knowledge acquisition (in interaction with medical

experts), (2) automatically by machine learning

algorithms (from available medical data sets), where

it is possible to learn network structure and

conditional probabilities separately.

The machine learning approach is especially

useful in the medical domain where it is very hard to

explicitly state medical knowledge, and on the other

hand there already are plenty of available medical

data sets. With arrival of new patient data the

network can be updated and improved. If the

environment of the network is changed (e.g. the

system is applied in another country), new network

can be obtained by learning on new data set.

Figure 1 shows a provisional example of BN that

was built manually and that is used in the paper for

methodology demonstration purposes (from heart

Figure 1: Provisional BN for diagnosing heart failure

disease.

HEALTHINF 2010 - International Conference on Health Informatics

236

failure domain). Based on defined conditional

probabilities it is possible to calculate probabilities

(beliefs) of each outcome of each node in the

network (e.g. expecting normal ejection fraction in

70% cases).

In cases when physician is uncertain about the

diagnosis she should perform additional diagnostic

tests. In that case it would be very useful to know

which medical tests are the most appropriate in

currently observed patient situation. In other words,

it is useful to calculate IG of each observation node

for each target node. There are many measures

which could be appropriate in this situation; the

expected decrease of entropy is a measure which is

most commonly used (Jagt 2002).

To calculate the entropy of the target node we

use the probabilities of all outcomes of the target

node:

ppXEXEntropy

log)()(

∑

−==

where X is a target node and o is the outcome of the

target node. The maximum value of entropy is 1

(when considering only two possible outcomes: Y

and N

O) and it is reached when the information

about the target node is completely uncertain (when

P(Y

ES) = P(NO) = 0.5). As probability of target node

approaches towards ends (0 and 1) the entropy is

falls into zero. It is better to have the entropy values

as close to zero as possible since that indicates that

the answer to the target question is clearer.

A summary measure which takes all possible

outcomes of diagnostic test into account is called

expected entropy which is calculated as follows:

),|(),( dDXEpDXtropyExpectedEn

∑

where X is target node, D is observation node, d

is a single outcome of node D, p

is probability of

occurrence of d outcome, and E(X|D=d) is the

entropy of the target node X when outcome d has

happened. It can be shown that in any BN value of

expected entropy cannot be raised by any diagnostic

test, only lowered (Jagt 2002).

When the procedure described above is repeated

for all observation nodes, a diagram shown on

Figure 2 is obtained. The figure indicates that for

reaching the final decision whether patient has or

has not diastolic heart failure the most informative

diagnostic tests is measuring diastolic blood

pressure. After physician actually measures diastolic

blood pressure beliefs in the network are updated.

Accordingly, observation nodes are updated with

fresh IG values. Such reasoning procedure in BN is

referenced in the literature as “explaining away”.

Figure 2: IG of all diagnostic nodes for target concept

IASTOLICHF, for a patient that has not performed a single

diagnostic test yet.

4 STRUCTURED MEDICAL

DIAGNOSTIC TESTS

In medical practice some diagnostic measurements

are never performed separately (e.g. systolic and

diastolic blood pressure). Ontology provides a

framework for organizing all possible diagnostic

tests into groups as they appear in medical practice.

In the ontology grouped diagnostic tests are

organized easily by arranging the ontology structure

as shown on Figure 3.

Figure 3: Diagnostic tests are defined within ontology.

The figure shows which elementary diagnostic

values are measured by performing blood pressure

measurement grouped diagnostic test. Besides

identifying blood pressure measurement as an

independent test, it is at the same time a constituent

part of a more thorough tests which is called

physical examination. In this manner it is possible to

organize diagnostic tests into groups and subgroups.

Additionally, some elementary observation can be a

part of two different tests; e.g. heart rate can be

measured both on physical examination and on

INFORMATION GAIN OF STRUCTURED MEDICAL DIAGNOSTIC TESTS - Integration of Bayesian Networks and

Ontologies

237

ECG. Grouped diagnostic tests are not necessarily

disjunctive.

4.1 Outcomes of Structured Tests

Difficulty with structured diagnostic tests is that the

number of possible outcomes grows extremely fast.

Namely, it is equal to the product of number of

outcomes for every elementary test in the group. For

example, if group blood pressure measurement has

only two elementary measurements (systolic and

diastolic) where each has three possible outcomes

(high, normal, low), there are nine possible

outcomes of such test. It is evident that the growth

rate of total number of outcomes in the group is of

combinatorial nature.

4.2 Information Gain of Structured

Medical Test

Formally speaking, to calculate the IG of a group for

every possible outcome g of the group G one must

calculate (1) the a priori probability of occurrence of

observed group outcome p

, and (2) entropy of the

target concept when observed outcome g happens E

= E(X | G = g). Then the expected entropy of the

target concept is equal to:

∑

EpGXtropyExpectedEn ),(

where X is observed target node and G is observed

grouped diagnostic test.

To find exact value of probability p

it is possible

to construct a dummy node in the BN which would

have all nodes from the observed group as parent

nodes and conditional probability table defined as

truth table which evaluates to Y

ES only in the

column of the observed outcome g. When network

beliefs are updated the belief of outcome Y

ES in that

node will be equal to p

. By setting the evidence on

the same dummy node to the outcome YES one

could read out the a posteriori probability of the

observed target node and thus calculate value E

This procedure should be repeated (1) for every

possible outcome, (2) of every possible diagnostic

group test, and (3) for every possible target node.

With large number of target nodes, large number of

grouped diagnostic tests and large number of

possible outcomes the procedure becomes extremely

computationally demanding. This calls for other

potential solutions which would compute in more

acceptable time.

One possibility for solving this issue is to use the

sampling algorithms. Namely, it is possible to

generate arbitrarily large set of samples (artificial set

of patients) depending on the properties of the BN

and depending on patient evidence that is present

and to use it to calculate required probability values.

The same procedure applies with grouped tests:

samplesofnumber

goutcomewithsamplesofnumber

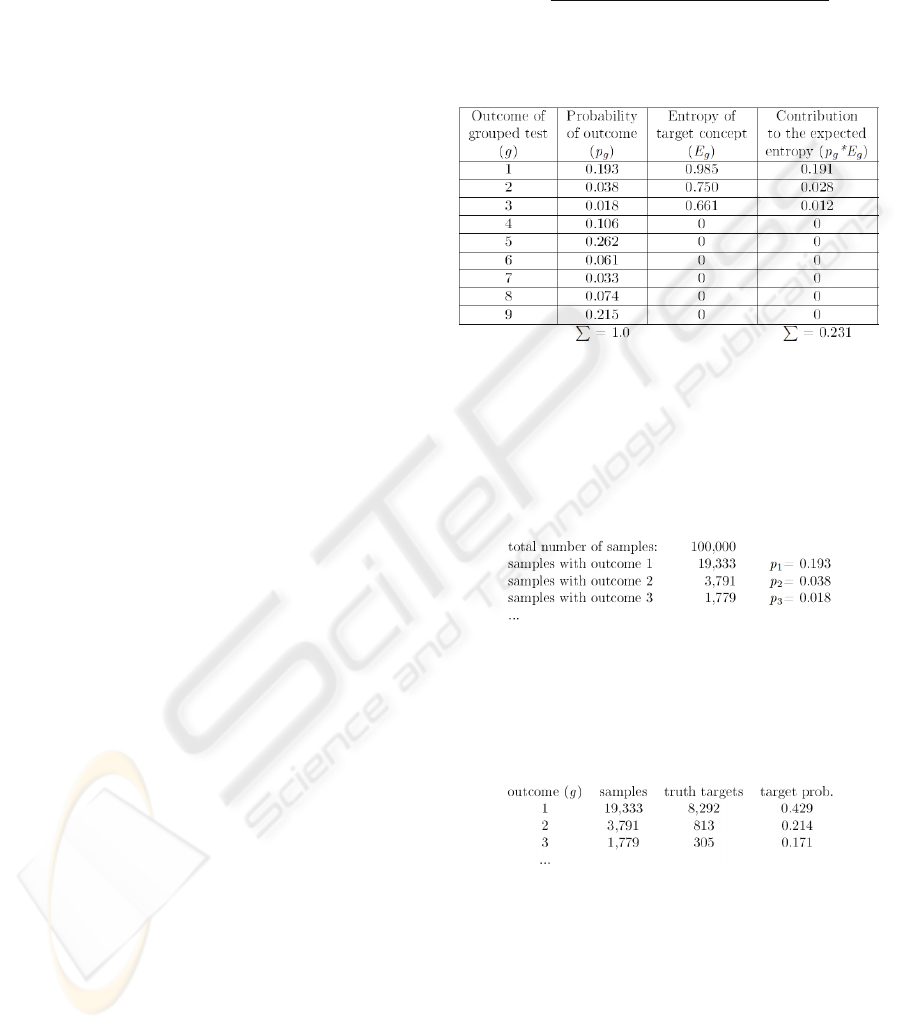
Table 1: Calculating the expected entropy of the target

concept with respect to the grouped diagnostic test.

Table 1 explicates the procedure for computing

the expected entropy (0.231) of the target node

IASTOLIC HF) after performing grouped diagnostic

test (measuring blood pressure). By counting the

number of samples with observed outcome one

calculates probabilities of outcomes p

(second

column of Table 1):

This way the initial set of samples has been

divided (unevenly) into nine disjoint subsets. In each

subset it is possible to count samples for which the

target node was assigned with positive diagnosis.

This way a posteriori target probabilities are also

calculated from the same sample set:

Now it is also possible to calculate the a

posteriori entropy values and also the final IG value.

5 USAGE EXAMPLE

By starting the decision support services physician

finds out probabilities of diseases for the observed

patient considering all currently known patient data.

An example is shown on Figure 4. When the

analysis of IG for all defined grouped diagnostic

HEALTHINF 2010 - International Conference on Health Informatics

238

tests in the ontology is performed, the physician can

find out which test is the most informative one

considering observed target nodes. Figure 5 shows

the example results of such analysis.

Figure 4: Probabilities of target nodes for observed patient

considering all currently known patient data.

Figure 5: IG of ontologically organized diagnostic tests

considering the target concept “Heart failure signs”.

Medical interpretation of results shown on Figure

5 is following: considering all his currently known

data and considering all previously recorded cases of

the disease (cases which are inherently encoded

within BN) observed patient has 60% possibility of

having heart failure signs. If physician wants to be

more certain he can perform some additional

medical tests. Analysis of IG (again, considering all

known patient data and considering all previously

recorded cases) indicates that physical examination

is the most informative test that can be performed.

Physical examination contains more diagnostic

tests one of which is measuring blood pressure,

which can be further divided into measuring

diastolic and systolic blood pressure (structure

defined within the ontology). All such tests (both

grouped and elementary) have their own IG value.

A different view of the results is also possible:

one can compare the summary impacts of grouped

diagnostic tests on defined target concept. Figure 6

demonstrates the comparison of two diagnostic tests:

echocardiography and physical examination. This

way physician can compare the overall values of IG

of all medical tests which helps him to make a

decision which medical test (tests) should be

performed next.

Figure 6: Comprehensive view of IG of available medical

diagnostic tests.

6 PERFORMANCE

Behaviour of the system in a great deal depends

upon some inherent characteristic both of the

ontology and the BN. Within this paper

measurements are conducted using a single specific

BN and a single specific ontology; hence, the

analysis is merely a preview of some provisional

setting. However, we assume that behaviour of a

single problem instance at least to some extent

indicates its general behaviour.

The main concern in the performance of the

described system is with (1) time required for

reasoning and (2) error made in reasoning.

Furthermore, it is evident that there is a trade-off

between those two parameters.

Figure 7: Standard error made in reasoning depends upon

number of elementary measurements in the test and the

number of samples.

Figure 7 shows the dependency of error made in

the reasoning process upon the number of

elementary measurements in the test and the number

of samples used. For example, if one is calculating

the IG of some grouped test which contains 10

elementary measurements using 50,000 samples

INFORMATION GAIN OF STRUCTURED MEDICAL DIAGNOSTIC TESTS - Integration of Bayesian Networks and

Ontologies

239

standard error made in calculations will be

somewhere near 1%.

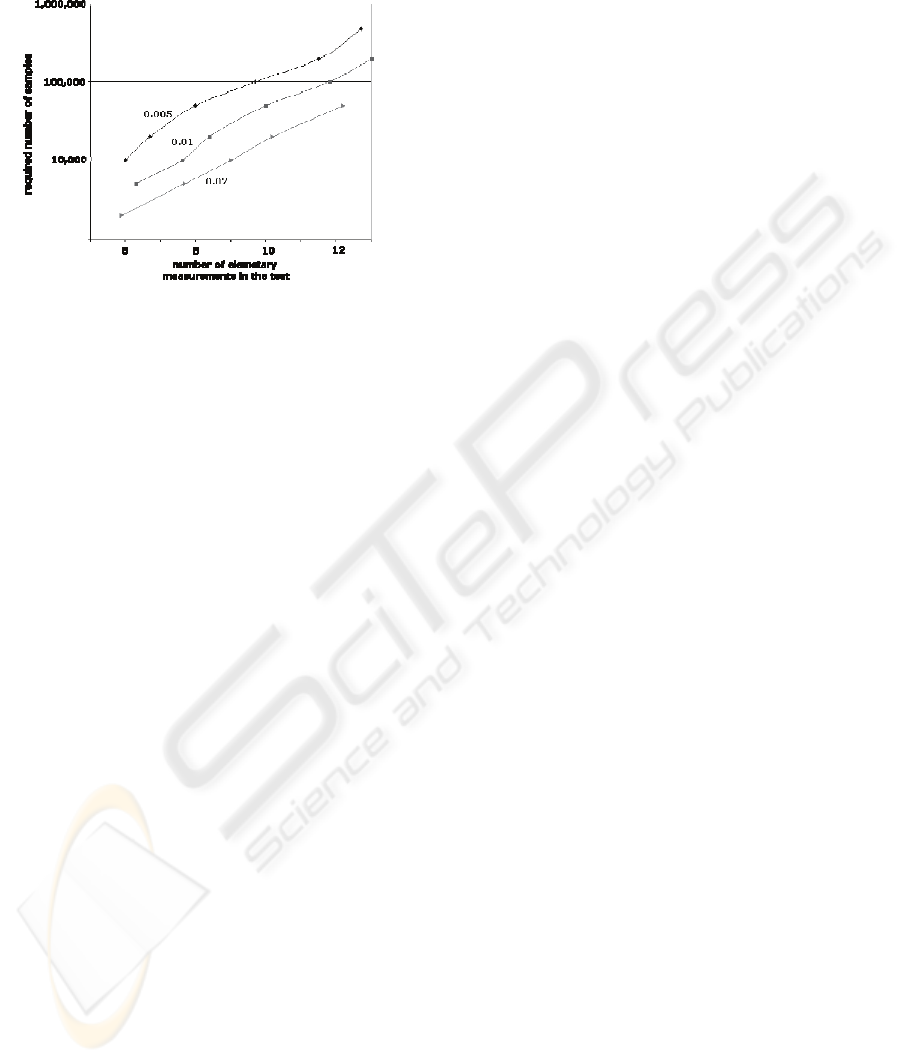
Figure 8: The appropriate number of samples depends on

used number of elementary measurements in the tests and

on chosen error rate.

Figure 8 is indicating a minimum number of

samples one should use depending on sizes of

defined groups in the ontology and on chosen error

rate. E.g., if one is satisfied with error rate of 1% and

has up to 12 elementary measurements in a group

she should use at least 100,000 samples in reasoning

phase. Chart depicts such relation for error rates of

2%, 1% and 0.5%.

7 CONCLUSIONS

In this paper we have demonstrated the approach for

integration of knowledge from BNs and ontologies

in order to calculate the IG of structured medical

test. We strongly believe that the approach is sound

and can be very useful in practical medical decision

support systems.

The main obstacle in the described methodology

appeared to be the combinatorial nature of the

number of outcomes in grouped diagnostic tests.

However, practical experiments indicate that this

obstacle in some cases can be to some extent

avoided by usage of sampling algorithms in the

reasoning phase. The measurements have

demonstrated the dependency of error rate and

required number of samples. On that basis, and

considering some specific system properties such as

number of nodes in the network, sizes of grouped

diagnostic tests, acceptable time of reasoning,

acceptable error rate, and properties of machine that

performs reasoning, one can conclude which number

of samples should she use in the reasoning phase.

Structure of BNs inherently assumes conditional

independency – an assumption that in general case

does not stand for medical diagnostic tests. In spite

of that, vast majority of decision support systems

that make use of BNs ignore this issue. However,

one should be fully aware of this drawback when

using proposed methodology in practice.

Suggested methodology of integration of BNs

and ontologies still calls for more thorough testing

of its overall performance and has yet to

demonstrate its practical utility in real medical

environments. Furthermore, suitability of the

approach in some other domains remains to be

shown. All above mentioned problems seem to be

rather interesting topics for the future work.

REFERENCES

Pan, R., Ding, Z., Yu, Y., Peng, Y. (2005). A Bayesian

Network Approach to Ontology Mapping. Fourth

international Semantic Web Conf. 2005, 563-577.

Devitt, A., Danev, B., Matusikova, K. (2006).

Constructing Bayesian Networks Automatically using

Ontologies. Ontology Meet Industry workshop 2006.

Town, C. (2004). Ontology-driven Bayesian Networks for

Dynamic Scene Understanding. IEEE Computer

Society Conference on Computer Vision and Pattern

Recognition Workshops 2004.

McGarry, K., Garfield, S., Wermter, S. (2007). Auto-

Extraction, Representation and Integration of a

diabetes Ontology using Bayesian Network.

Computer-Based Med. Sys. Symposium ’07, 612-617

Huhns, M.N., Valtorta, M.G. (2007). Ontological Support

for Bayesian Evidence Management. Ontology for the

intelligence community 2007, 47-51.

Wang, W., Zeng, G., Zhang, D., Huang, Y. et al. (2008).

An intelligent Ontology and Bayesian Network based

Semantic Mashup for Tourism. IEEE Congress on

Services, part I, 128-135.

Jeon, B.J., Ko, I.Y. (2007). Ontology-Based Semi-

Automatic Construction of Bayesian Network Models

for Diagnosing Diseases in E-health Applications.

Frontiers in the Convergence of Bioscience and

Information Technologies, fbit, pp.595-602

Zheng, H.T., Kang, B.Y., Kim, H.G. (2005). An

Ontology-based Bayesian Network Approach for

Representing Uncertainty in Clinical Practice

Guidelines, Uncertainty Reasoning for the Semantic

Web workshop 2005.

Jagt, R.M. (2002). Support for multiple cause diagnosis

with Bayesian Networks. Thesis for degree of Master

of Science in Applied Mathematics. Information

Sciences department, University of Pittsburgh, USA.

HEALTHINF 2010 - International Conference on Health Informatics

240