A MULTI-AGENT MPC ARCHITECTURE FOR DISTRIBUTED

LARGE SCALE SYSTEMS

Valeria Javalera, Bernardo Morcego and Vicenç Puig

Advanced Control Systems Group, Institut de Robòtica i Informàtica Industrial, CSIC-UPC

C/. Llorens i Artigas, 4-6, 08028 Barcelona, Spain

Keywords: Large scale systems, Multi agent systems, Distributed model predictive control, Reinforcement learning.

Abstract: In the present work, techniques of Model Predictive Control (MPC), Multi Agent Systems (MAS) and

Reinforcement Learning (RL) are combined to develop a distributed control architecture for Large Scale

Systems (LSS). This architecture is multi-agent based. The system to be controlled is divided in several

partitions and there is an MPC Agent in charge of each partition. MPC Agents interact over a platform that

allows them to be located physically apart. One of the main new concepts of this architecture is the

Negotiator Agent. Negotiator Agents interact with MPC Agents which share control variables. These shared

variables represent physical connections between partitions that should be preserved in order to respect the

system structure. The case of study, in which the proposed architecture is being applied and tested, is a

small drinking water network. The application to a real network (the Barcelona case) is currently under

development.

1 INTRODUCTION

Large Scale Systems (LSS) are complex dynamical

systems at service of everyone and in charge of

industry, governments, and enterprises. The

applications are wide. Examples of applications of

LSS in continuous domains are: power networks,

sewer networks, water networks, canal and river

networks for agriculture, etc. Other examples of

applications of LSS in discrete domain are traffic

control, railway control, manufacturing industry, etc.

Experts in automatic control have developed

many solutions for this kind of systems. However,

the increase of automation of LSS renders problems

with a noticeable increase in complexity. Such

complexity is due to the size of the system to be

controlled and the huge number of sensors and

actuators needed to carry out the control.

Additionally, LSS are composed of many interacting

subsystems. Thus, LSS control is difficult to be

implemented using a centralized control structure

because of robustness and reliability problems and

due to communication limitations. For all these

reasons, distributed control schemes have been

proposed over the last years.

One of the main problems of distributed control

of LSS is how relations between system partitions

are preserved. These relations could be, for example,

pipes that connect two different control zones of a

decentralized water transport network, or any other

kind of connection between different control zones.

When these connections represent control variables,

the distributed control has to be consistent for both

zones and the optimal value of these variables will

have to accomplish a common goal.

The authors believe that this open problem in

control theory can be solve by the combination of

adequate control and computer science techniques,

more precisely, the combination of Model Predictive

control (MPC), Multi-Agent Systems (MAS), and

Reinforcement Learning (RL).

Due to Distributed Control (DC) present the

same philosophy of Distributed Artificial

Intelligence (DAI), the idea is to apply MAS

techniques and technology to DC problems as

communication, coordination, need of adaptation

(learning), autonomy and intelligence.

The use of RL in the negotiation process will

allow to:

1) Make the process of negotiation adaptive; 2)

Learn from its own experience; 3) Explicitly

consider the whole problem of two goal-oriented

agents; 3) Deal with a dynamical and uncertain

environment; 4) Optimize with or without a model;

544

Javalera V., Morcego B. and Puig V. (2010).

A MULTI-AGENT MPC ARCHITECTURE FOR DISTRIBUTED LARGE SCALE SYSTEMS.

In Proceedings of the 2nd International Conference on Agents and Artiﬁcial Intelligence - Artiﬁcial Intelligence, pages 544-551

DOI: 10.5220/0002715805440551

 SciTePress

5) Connect the process of negotiation whit the one of

the control MPC, this because of compatibilities

found between them.

Model Predictive Control (MPC), also known as

receding horizon control, is a control technique

widely used in industry (see (Qin & Badwell, 2003)

and (Camacho & Bordons, 2004)) well suited for the

control of continuous LSS. In MPC, the control

input is obtained by solving a discrete-time optimal

control problem over a given horizon, producing an

optimal open-loop control input sequence. The first

control in that sequence is applied. At the next

sampling instant, a new optimal control problem is

formulated and solved based on the new

measurements.

The MPC control aim is to find actions

, …, u

k+Nc

, such that after N

steps, a sequence of

predicted outputs y approaches a set point y

The theory of MPC is well developed; most

aspects, such as stability, nonlinearity, and

robustness, have been discussed in the literature

(see, e.g., (Bemporad & Morari, 1999) (Morari &

Lee, 1999). Besides, MPC is very popular in the

process control industry because the actual control

objectives and operating constraints can be

represented explicitly in the optimization problem

that is solved at each control instant.

Typically, MPC is implemented in a centralized

fashion. The complete system is modelled, and all

the control inputs are computed in one optimization

problem.

The goal of the research described in this paper is

to exploit the attractive features of MPC (meaningful

objective functions and constraints) in a distributed

implementation combining learning techniques to

perform the negotiation of these variables in a

cooperative Multi Agent environment and over a

Multi Agent platform. All these ideas are the basis

of the proposed architecture. A methodology for the

application of the proposed architecture is also

provided.

Organization of the paper is as follows: Section

2 introduces the problem to be solved and Section 3

describes known approaches to it based on

distributed MPC. The formalization of the proposed

architecture is given in Section 4. Section 5 and 6

are devoted to an application example and the results

obtained. Finally, Section 7 presents the paper

conclusions and Section 8 presents the current and

further research that is being developed.

2 THE PROBLEM

In order to control a LSS in a distributed way, some

assumptions have to be made on its dynamics, i.e. on

the way the system behaves. Assume, first, that the

system can be divided into n subsystems, where each

subsystem consists of a set of nodes and the

interconnections between them. The problem of

determining the partitions of the network is not

addressed in this paper; instead the reader is referred

to (Siljack, 1991). The set of partitions should be

complete. This means that all system states and

control variables should be included at least in one

of the partitions.

Definition 1. System Partitions. P is the set of

system partitions and is defined by

},,,{

21 np

pppP …

(1)

where each system partition (subsystem) p

described by a deterministic linear time-invariant

model that is expressed in discrete-time as follows

)()()()(

)()()()1(

kkkk

iidiiuiii

dDuDxCy

dBuBxAx

++=

(2)

where variables x, y, u and d are the state, output,

input and disturbance vectors, respectively; A, C, B

and D are the state, output, input and direct matrix,

respectively. Subindices u and d refer to the type of

inputs the matrix model, either control inputs or

disturbances.

Definition 2. Internal Variables. Internal variables

are control variables that appear in the model of only

one subsystem in the problem. The set of internal

variables of one partition is defined by

},,,{

21 nu

uuuU …

(3)

Definition 3. Shared Variables. Shared variables

are control variables that appear in the model of at

least two subsystems in the problem. Their values

should be consistent in the subsystems they appear,

so they are also called negotiated variables. V is the

set of negotiated variables defined by

},,,{

21 nv

vvvV …=

(4)

Each subsystem i is controlled by an MPC

controller using:

- the model of the dynamics of subsystem i

given by equation (2);

- the measured state x

(k) of subsystem i;

A MULTI-AGENT MPC ARCHITECTURE FOR DISTRIBUTED LARGE SCALE SYSTEMS

545

- the exogenous inputs d

(k+1) of subsystem

i over a specific horizon of time;

As a result each MPC controller determines the

values u

(k) of subsystem i. The internal control

variables are obtained directly by the MPC

controller of this subsystem while the shared

variables are proposed to be negotiated with the

MPC controllers of the corresponding subsystem.

When there are no shared variables between

subsystems, this control scheme is usually referred

to as decentralized control. When the set of shared

variables is not empty, it is usually referred to as

distributed control. The problem addressed in this

paper is an agent based distributed control. There is

one agent in charge of each system partition and its

duties are to negotiate the shared variables with

other agents and to calculate the control actions from

the MPC formulation of its partition.

Figure 1, on the left, shows a sample system

divided into three partitions. There are three

overlapping sets that contain four shared variables.

The relations that represent those variables are

shown on the right as lines. The problem consists in

optimizing the manipulated variables of the global

system in a distributed fashion, i.e. with three local

control agents that must preserve consistency

between the shared variables.

Figure 1: The problem of distributed control.

3 DISTRIBUTED MPC

In distributed control schemes, local control inputs

are computed using local measurements and

reduced-order models of the local dynamics

(Scattolini, 2009).

Distributed MPC is attractive because it requires

only local process data for controller design and

model maintenance. Computing demands are

smaller on each control agent. Furthermore, routine

maintenance operations such as removing sensors or

actuators for repairing are achieved much more

easily under distributed MPC. Nevertheless, there is

one well known drawback: the performance of

distributed MPC is usually far from optimal when

the subsystems interact significantly. Centralized

MPC, on the other hand, achieves optimal nominal

control for any system. However, centralized MPC

is viewed by most practitioners as impractical and

unsuitable for control of large networked systems.

(Venkat et al., 2005).

Distributed MPC algorithms are classified into

iterative and non-iterative and further subclassified

into independent or cooperative algorithms.

In iterative algorithms information is bi-

directionally transmitted among local regulators

many times within the sampling time. In non-

iterative algorithms information is bi-directionally

transmitted among local regulators only once within

each sampling time. (Scattolini, 2009) gives a

review of distributed control architectures for LSS.

Independent (non-cooperative) algorithms are

widely studied in game theory. Their aim is to get

better results than the other controllers, which are

seen as opponents. They have also been applied in

MPC distributed control strategies [see, for instance,

(Jia & Krogh, 2002) (Camponogara, 2002)].

Contrarily, cooperative algorithms intend to find

a compromise for shared variables in order to

maximize the performance of the complete system,

worsening if necessary the performance of

partitions. (Negenborn et al., 2008) and (Venkat et

al., 2005) are two recent examples of the application

of cooperative algorithms, the first one is non-

iterative and the second one is iterative.

4 MULTI-AGENT MPC

ARCHITECTURE

In this section, the proposed multi-agent MPC

(MAMPC) architecture is presented. First the

elements of the proposed architecture are presented.

Then, the whole architecture is described.

4.1 Elements

The elements of the proposed architecture are: MPC

Agents and Negotiator Agents. They interact over an

Agent Platform that is composed by a set of Nodes.

Sub-division of the plant

Relations

between

controllers

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

546

Definition 4. MPC Agent. An MPC Agent is the

entity that is in charge of controlling one specific

partition of the system.

There is one MPC Agent for each system

partition. The MPC Agent solves an MPC control

problem considering the internal variables of the

partition and cooperating with one or more

Negotiator Agents to determine the optimum value

of the shared variables. A is the set of MPC Agents

},,,{

21 na

aaaA …=

(5)

Definition 5. Negotiator Agent. A Negotiator

Agent is the entity that is in charge of determining

the value of one or more shared variables between

two MPC Agents.

In this negotiation, each MPC Agent is arranged

to cooperate so that the negotiator agent solves the

optimization of a common goal by means of an

algorithm based on Reinforcement Learning. A

negotiator Agent exists for every pair of MPC

Agents that have one or more shared variables in

common. N is the set of Negotiator Agents defined

},,,{

21 nn

nnnN …=

(6)

Definition 6. Nodes. A node is the physical device

(commonly a computer) in which the agents are

located. W is the set of nodes defined by

},,,{

21 nw

wwwW …=

(7)

There is a node for each MPC Agent. Nodes are

communicated via some communication

infrastructure (LAN, WAN or Internet).

Definition 7. Agent Platform. The agent platform

works as a virtual machine providing the agents a

homogenous medium to communicate and providing

the user a way to manage agents. The agent platform

is denoted by b.

This platform has to be installed and running in

all nodes.

4.2 Architecture

Definition 8. MAMPC Architecture. The MAMPC

distributed control architecture is defined as:

},,,,,,{ bUVWPNA

nann

(8)

where: A is the set of MPC Agents, N is the set of

Negotiator Agents, P is the system partitions, W is

the set of nodes, V

is the set formed by all sets of

Shared Variables, U

is the set formed by all sets of

Internal Variables and b is the Agent platform.

A methodology has been developed to apply this

MAMPC architecture in a given system. This

methodology will be illustrated in the following

section with an example.

4.3 Cooperation of MPC-Agents

The cooperative interaction of MPC agents is a basic

issue in the proposed approach. Three main actions

are necessary to perform this cooperation:

 To perform actions and provide data required

by the Negotiatior Agent

 To accept the value(s) provided by the

Negotiator Agent of its shared variable(s).

 To solve the MPC control problem of its

partition, adjusting the value(s) of its shared

control variable(s) in order to coordinate the

solution of the negotiation.

The Negotiator Agent determines the optimal

value of the values in set V

. This set contains the

shared variables of two, and just two MPC Agents.

The Negotiator Agent optimizes them through a

Negotiation algorithm based on Reinforcement

Learning (RL). Each shared variable is an

optimization problem. This problem is solved as a

whole looking for the optimal value of the relation.

The method is based on the reinforcements given at

each step and on the experience obtained. This

experience is stored in a knowledge base, one for

each negotiation variable.

In the distributed model of the system, shared

variables appear in the local models of each MPC

Agent involved in the relation, therefore they end up

duplicated.

The Negotiator Agent restores the broken

connections when the system was partitioned,

unifiying this duplicate variables in a single one, just

as in the original model. Therefore, for the

Negotiator Agent, this two control variables are

taken as one.

The philosophy of the proposed negotiation

algorithm is to consider the shared variables as

belonging to a single problem with a single goal,

instead of two different problems with conflicting

goals. The Negotiator Agent solves the optimization

problem for that variable and communicates the

result to the MPC Agents at each sampling time.

Then, MPC Agents set those values as a hard

constraint in its respective internal control variables

and recalculate the multivariable control problem.

The optimization of the Negotiator Agent

algorithm is based on its experience and on

maximizing the reinforcements received at every

action taken in the past on similar situations.

A MULTI-AGENT MPC ARCHITECTURE FOR DISTRIBUTED LARGE SCALE SYSTEMS

547

This algoritm is based on the Q-learning

algorithm, and adapted to be applied in dynamical

environments. Next, the formulation of the

algorithm is detailed.

4.3.1 Formulation of the Negotiation-

learning Problem

The goal of the Negotiator Agent is to detemine the

optimal value of the set of shared variables V

. Each

element of the set V

is an optimization problem

addressed individually by the Negotiator Agent and

there is a knowledge base for each one. The internal

architecture of the Negotiator Agent comprises the

following elements:

 A set of knowledge bases (Q-tables); each Q-

table represents the knowledge base of the

agent, which has a Q-table for each shared

variable because each one can have diferent

behaviour and even different goals.

 A communication protocol that allows it to

have bi-directional communication with two

MPC-Agents.

 A negotiation algorithm

Next, these elements are described in further

detail.

Q-Table. The Q-table represents the knowledge

base of the agent, which has a Q-table for each

shared variable because each one can have diferent

behaviour and even different goals.

Q-tables maintain the reinforcement gained for

each possible state and action. A state represents the

global state of each sub-problem, which is

established in terms of the error of the output with

respect to the goal. The definition of the error that

MPC Agents use is:

iii

yg −=

(9)

where ε

is the error, g

is the goal and y

is the

output of variable i.

The state value is determined by:

21 ii

εε

(10)

where ε

is the error of the variable i of first agent,

and ε

of the corresponding variable in the second

agent. This state is updated every sampling time.

Since states are continuous, they have to be

discretized for the application of the RL algorithm.

Actions are all the posible values that the shared

variable can take. Since actions are continuous, they

have to be discretized for the application of the RL

algorithm.

The reward function determines the reward of

every action taken by the agent. In this case, the

reward function is:

−

(11)

where ρ is a value greater or equal than s

Communication Protocol. MPC Agents start the

comunication by interchanging the resulting output

of the control applied (y

(k)), the vector of controls

applied (u

(k)), the absolute error whith respect to the

goal of the shared variable ε

(k) and the sampling

time k. Then, the algorithm of the Negotiator Agent

is executed. When it finishes, it communicates the

result of the optimization and the parameters needed

by de MPC Agents to solve their multivariable

problems, taking as restrictions the values given by

the negotiator. Then the procces starts again.

Negotiation Algorithm. This algorithm is divided in

two phases, the training phase and the exploitation

phase. In both cases, the updated rule for Q-table

values is:

)),((),( asQrasQ ×

(12)

The training phase creates a new Q-table off-line

using stored data obtained, for instance, from the

control actions determined by the centralized

approach.

Once the Q-table is initialized, the exploitation

phase can start. The main difference here is that

actions are chosen according to

)),((max' asQa

(13)

in order to select for the next time instant, the value

of the action (negotiated variable) with maximum

reward

5 APPLICATION EXAMPLE

5.1 Description

A small drinking water network is used to exemplify

the proposed MAMPC architecture. The example

was proposed in (Barcelli, 2008) where a centralized

and a decentralized solution was studied and

compared. This hypothetical water distribution

network has 8 states (tanks) and 11 control variables

(valves). It has been divided into two subsystems.

Two MPC Agents are used to determine the internal

control variables of each subsystem. Furthermore,

one Negotiator Agent is responsible of negotiating

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

548

the values of the two shared control variables

between the two MPC agents (see Figure 2).

5.2 Analysis

In the analysis phase, the MAMPC Architecture is

defined. This phase comprises the following tasks:

Definition of the Optimization Goals. The control

goal of the application presented in Figure 2 is to

keep a water volume in each tank around 3m

Partitioning of the Network. The system is splitted

into two partitions:

Figure 2: Case study and its partitioning.

},,,,{

654211

xxxxxp =

(14)

},,{

8732

xxxp =

(15)

},{

1110

uuV =

(16)

},,,,,{

9876211

uuuuuuU =

(17)

},,{

5432

uuuU =

(18)

The plant is defined by all its state and input

variables

},,,,,,,,

,,,,,,,,,,{

11109876543

2187654321

uuuuuuuuu

uuxxxxxxxxPlant =

(19)

An important step is to check that the

partinioning of the plant leads to a complete set of

partitions. This is accomplished verifying the

following relation:

VUPPlant ∪∪=

(20)

which can be easily verified,

VUUppPlant ∪∪∪∪=

2121

(21)

Thus, the partition is a complete set of partitions.

Definition of the Architecture. In this step, the

MAMPC Architecture is defined for the water

network case study. Considering the definition of

the architecture in (8), the remaining elements are

defined as follows:

},{

aaA

(22)

}{

(23)

},{

wwW

(24)

Inclusion of Restrictions and Considerations. The

maximum water volume in tanks is 20m

, the control

value of the measured variables ranges from 0.0 to

0.4 except for u

that it ranges from 0.0 to 0.1. The

sampling time is 1 hour and the prediction horizon is

24 hours. The demands are considered as measured

perturbations. They typically present a sinusoidal

behaviour throghout the day.

5.3 Design

In the design process, the subproblems of every

MPC Agent and Negotiator Agent are formulated.

This formulation is based on the information

collected in the analysis phase that allows to know

the internal structure of the MPC Agents.

The core of the MPC agent is a MPC controller.

This controller solves the multivariable problem of

one partition of the plant based on a model. This

model contains the set u

of the agent. Other

important part of the MPC Agent is the

communication block. MPC Agents can

communicate in a sophisticated way because they

are implemented using the Agent Oriented

Paradigm. This paradigm provides methods,

standards and tools that allow good communication

skills.

Formulation of the MPC Problem. In this step, all

the MPC parameters and requierements have to be

defined for both agents, such as:

1)The plant; 2) The measured, non-measured and

manipulated variables; 3) Limits and constraints; 4)

The negotiation variables are set as restrictions; 5)

References (goals); 6) Prediction horizon; 7) Control

Horizon; 8) Initial state; 9) Perturbations models

All these data have to be set in all MPC Agents.

The prediction and control horizon should be the

same for all MPC Agents.

5.3.1 Training and Exploitation

As in any RL algorithm, the proposed architecture is

based on the agent experience and the expected

reinforcements. The richer the agent experience has

been, the more efficient the optimization algorithm

will be.

A MULTI-AGENT MPC ARCHITECTURE FOR DISTRIBUTED LARGE SCALE SYSTEMS

549

An off-line training was done in order to provide

this experience to the Negotiatior Agent. First,

control actions determined from a 48 hours scenario

of the centralized approach were used as

initialization values for the agent training process.

From this point, the training continued taking

random actions The reward was calculated for all

actions.

In the RL exploitation phase the knowledge

adquired in the exploration (and training) phase is

used.

The exploitation phase uses the knowledge

adquired in order to solve the MPC distributed

problem through the MA system.

6 RESULTS

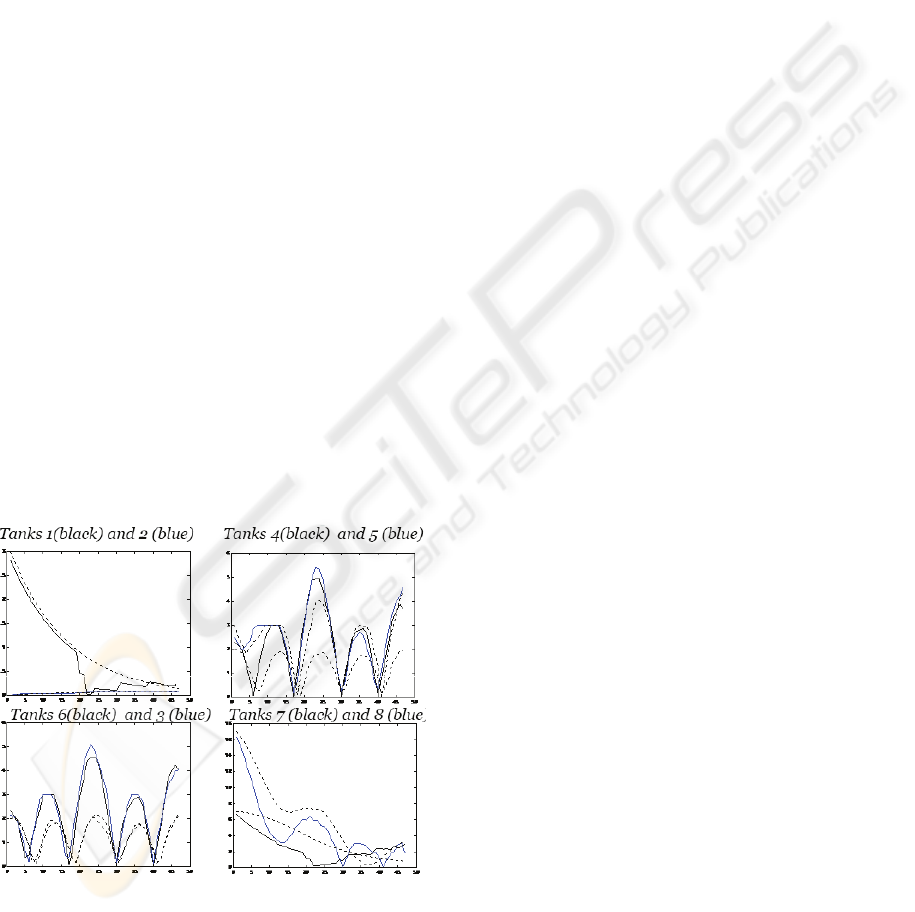
The results obtained using the proposed MAMPC

Architecture are shown in Figure 3. Each graph

presents a 48 hour scenario, showing the absolute

error with respect to the goal (volume of 3m

in each

tank) at every time step. The results are contrasted

with the centralized solution (dashed line) for all

tanks.

The distributed solution was expected not to be

as good as the centralized one. However, the graphs

shows that, in some cases (tanks 1, 2, 7 and 8) the

distributed MAMPC Architecture solution is better.

It is important to note that the volume of tanks 1, 7

and 8 depends on the valute of the negotiated

variables (u

and u

Figure 3: Distributed MA-MPC Architecture solution

against centralized solution.

7 CONCLUSIONS

The results obtained suggest that the use of a Multi-

Agent control architecture based on negotiation can

converge to the centralized solution with an

acceptable degree of approximation but taking

advantage from the MAS properties and the tools

that the Agent Oriented Paradigm (AOP) provides

for development and implementation. Even more,

the application of learning techniques can provide

the Negotiatior Agent the ability of prediction.

Training of the negotiator can be made directly from

a centralized MPC or from human operator driven

control. In order to achieve optimization, no model

is needed by the negotiator. Data from centralized

MPC is advisable but not essential. The type and

quality of the training is a very important issue in

order to obtain an efficient optimization. Also the

compromise between exploration and explotation

can be implemented on line to enable the system not

just adaptation to the problem but adaptation to

changes in time. In this paper, this capability is not

addressed in training but in exploring during the

optimization. Communication protocols and

coordination methods for MAS have to be studied

and tested in a more complex case of study in which

many agents interact.

8 FURTHER RESEARCH

The MAMPC Architecture presented in this work is

currently being tested on the Barcelona water

transport network. The Barcelona water network is

comprised of 200 sectors with approximately 400

control points. At present, the Barcelona information

system receives, in real time, data from 200 control

points, mainly through flow meters and a few

pressure sensors. This network have been used as a

LSS case of study to test several LSS control

approaches, see (Brdys & Ulanicki 1994) and

(Cembrano et al, 2002) (Cembrano et al, 2004)

(Cembrano et al., 2000). As starting point for the

application of the MAMPC Architecture, recent

work on centralized (Caini et al., 2009) and

decentralized MPC (Fambrini & Ocampo, 2009)

applied to the Barcelona network is being used, as

well as, the partitioning algorithm developed by

(Barcelli, 2008).

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

550

ACKNOWLEDGEMENTS

This work is in the context of the European Project

Decentralized and Wireless Control of Large Scale

Systems, WIDE - 224168 - FP7-ICT-2007-2. First

author is sponsored by the Consejo Nacional de

Ciencia y Tecnología (CONACYT) of México and

is partially supported by the Instituto Tecnológico

Superior de Cajeme (ITESCA).

REFERENCES

Barcelli, D. (2008). Optimal decomposition of Barcelona´s

water distribution network system for applying

dsitribuited Model Predictive Control. Master thesis .

Universitat Politècnica de Cataluña-IRI-Universitá

degli Study di Siena.

Bemporad, A. and Morari, M. “Robust model predictive

control: A survey,” in Robustness in Identification and

Control (Lecture Notes in Control and Information

Sciences), vol. 245. New York: Springer-Verlag,

1999, pp. 207-226.

Brdys, M. A., & Ulanicki, B. (1994). Operational control

of water systems, Structures, Algorithms and

Applications. Great Britain: Prentice Hall

International.

Caini, E., Puig Cayuela, V., & Cembrano, G. (2009).

Development of a simulation environmet for water

drinking networks: Application to the validation of a

centralized MPC controller for the Barcelona Case of

study. Barcelona, Spain: IRI-CSIC-UPC.

Camacho, E. F., & Bordons, C. (2004). Model Predictive

Control. Springer-Verlag, London.

Cembrano, G., Figueras, J., Quevedo, J., Puig, V.,

Salamero, M., & Martí, J. (2002). Global control of

the Barcelona Sewerage system for environment

protection. IFAC.

Cembrano, G., Quevedo, J., Salamero, M., Puig, V.,

Figueras, J., & Martí, J. (2004). Optimal control of

urban drainage systems. A case of study. Control

Engineering Practice (12), 1-9.

Cembrano, G., Wells, G., Quevedo, J., Pérez, R., &

Argelaguet, R. (2000). Optimal Control of a water

distribution network in a supervisory control system.

Control of Engineering Practice (8), 1177-1188.

Fambrini, V., & Ocampo Martinez, C. (2009). Modelling a

decentralized Model Predictive Control of drinking

water network. Barcelona, Spain: IRI-CSIC-UPC.

Negenborn, R. R. (2008). Multi-Agent Model Predictive

Control with applications to power networks.

Engineering Applications of Artificial Intelligence ,

21, 353-366.

Negenborn, R. R., De Shutter, B., & Hellendoorn, J.

(2004). Multi-Agent model predictive control: A

survey. Technical report, Delf University of

Technology, Delf center for systems and control.

Qin, S. J., & Badwell, T. A. (2003). A survey of industrial

Model Predictive Control Technology. Control

Engineering Practice, 11, pp. 733–764.

Scattolini, R. (2009). Architectures for distributed and

hiearical Model Predictive Control- A Review. Journal

of Process Control , 723-731.

Siljack, D.D. (1991). Decentralized Control of Complex

Systems, Academic Press, New York.

Venkat, A. N., Rawlings, J. B., & Wrigth, S. J. (2005).

Stability and Optimality of distributed Model

Predictive Control. IEEE Conference on Decision and

Control / IEE European.

A MULTI-AGENT MPC ARCHITECTURE FOR DISTRIBUTED LARGE SCALE SYSTEMS

551