
COOPERA
TIVE LEARNING OF BDI ELEVATOR AGENTS
Yuya Takata, Yuki Mikura, Hiroaki Ueda and Kenichi Takahashi
Graduate School of Information Sciences, Hiroshima City University, Hiroshima 731-3194, Japan
Keywords:
Multiagent systems, BDI architecture, Reinforcement learning.
Abstract:
We propose a framework of cooperative learning of BDI agents. Our framework uses some kinds of agents,
including a task management agent (TMA) and rational agents. TMA is designed as a learning agent. It
manages assignment of tasks to rational agents. When a task is created, TMA evaluates the most useful strategy
on the basis of reinforcement learning. Rational agents also evaluate the value that the task is assigned to them
according to the strategy, and they give the value as their intention to TMA. Then, TMA optimally assigns the
task to a rational agent by using both the value and the rough strategies, and the rational agent processes the
task. In this article, we apply the proposed method to an elevator group control problem. Experiment results
show that the proposed method finds better task assignment than the methods without cooperative learning.
1 INTRODUCTION
In recent years, agent systems such as the RoboCup
soccer simulator (The RoboCup Federation, 2009)
and the multi-car elevator system (The IEICE Engi-
neering Sciences Society, Concurrent System Tech-
nology, 2009) have emerged as an active subfield of
artificial intelligence. In the agent circumstances, au-
tonomous agents are required to learn optimal rules
for their decision making or to infer their optimal be-
havior. Thus, many kinds of methods such as re-
inforcement learning (Sutton and Barto, 1998), evo-
lutionary computation (Katagiri et al., 2000) and
the BDI reasoning engine (Rao and Georgeff, 1991;
Doniec et al., 2006) have been proposed.
Reinforcement learning is one of traditional meth-
ods to learn optimal rules for agent behavior. It can
obtain optimal agent behavior efficiently for simple
agent circumstances such that agents can sense a few
percepts or cooperative behavior of agents is not re-
quired. For complex agent circumstances, however,
reinforcement learning requires quite a lot of trial and
error processes to learn the optimal agent behavior,
since the number of states increases exponentially as
the numbers of percepts and agents increase.
In Ref. (Excelente-Toledo and Jennings, 2003), it
is reported that anticipating other agent’s intention is
important for acquiring cooperative behavior. Ratio-
nal agents following the BDI (Belief Desire Intention)
model can anticipate other agent’s intention and infer
their optimal behavior. In order to infer the optimal
behavior, the designer of agent circumstances needs
to give a set of inference rules to the agents. For com-
plex agent circumstances, however, it is difficult for
the designer to design a set of rules.
In this article, we propose a framework of cooper-
ative learning of BDI agents. In a multiagent circum-
stance, it is difficult for the designer to give a set of in-
ference rules for optimizing cooperative behavior. On
the other hand, it is not difficult to give inference rules
optimizing behavior of a single agent and the designer
often has some rough strategies for optimizing coop-
erative behavior. Thus, we think that the pseudo op-
timal cooperative behavior is acquired by using both
inference rules for a single agent and the rough strate-
gies for cooperative behavior. In our framework, we
use two types of agents, a task management agent
(TMA) and rational agents. TMA manages assign-
ment of tasks to rational agents. For efficient task
assignment, TMA uses rough strategies given by the
designer. In order to learn which strategy is useful for
a current situation, TMA learns the policy to switch
strategies on the basis of reinforcement learning. Ra-
tional agents receive a task and the strategy selected
by TMA. They evaluate the value of the strategy as
their intention. Then, TMA optimally assigns a task
to a rational agent by using both the value and the
rough strategies, and the rational agent processes the
172
Takata Y., Mikura Y., Ueda H. and Takahashi K. (2010).
COOPERATIVE LEARNING OF BDI ELEVATOR AGENTS.
In Proceedings of the 2nd International Conference on Agents and Artificial Intelligence - Agents, pages 172-177
DOI: 10.5220/0002717201720177
Copyright
c
SciTePress

task. The framework is implemented and applied to
an elevator group control problem.
The rest of this paper is organized as follows. In
the next section, we briefly explain the elevator group
control problem and the implementation of the prob-
lem by using BDI agents. In Section 3, we present a
framework of cooperative learning of BDI agents. In
Section 4, we specify our elevator group control prob-
lem. Some experimental results are shown in Section
5. And finally, Section 6 concludes the paper.
2 IMPLEMENTATION OF BDI
ELEVATOR AGENTS
2.1 The Elevator Group Control
Problem
High-rise buildings have several shafts and cars (also
called cages) in order to transport passengers effi-
ciently. Recently, it is reported that a multi-car eleva-
tor system and elevator group control are effective for
transportation (Valdivielso et al., 2008; Ikeda et al.,
2008). In the system, buildings have several shafts
and there are two or more cars in each shaft. Passen-
gers resister their destination floor in the controller
and it schedules which car transports them. Then, the
controller guides the passengers to the scheduled car.
The objective of the elevator group control problem is
to develop the controller that transports passengers as
efficiently as possible.
2.2 Implementing the Problem as a BDI
Multiagent System
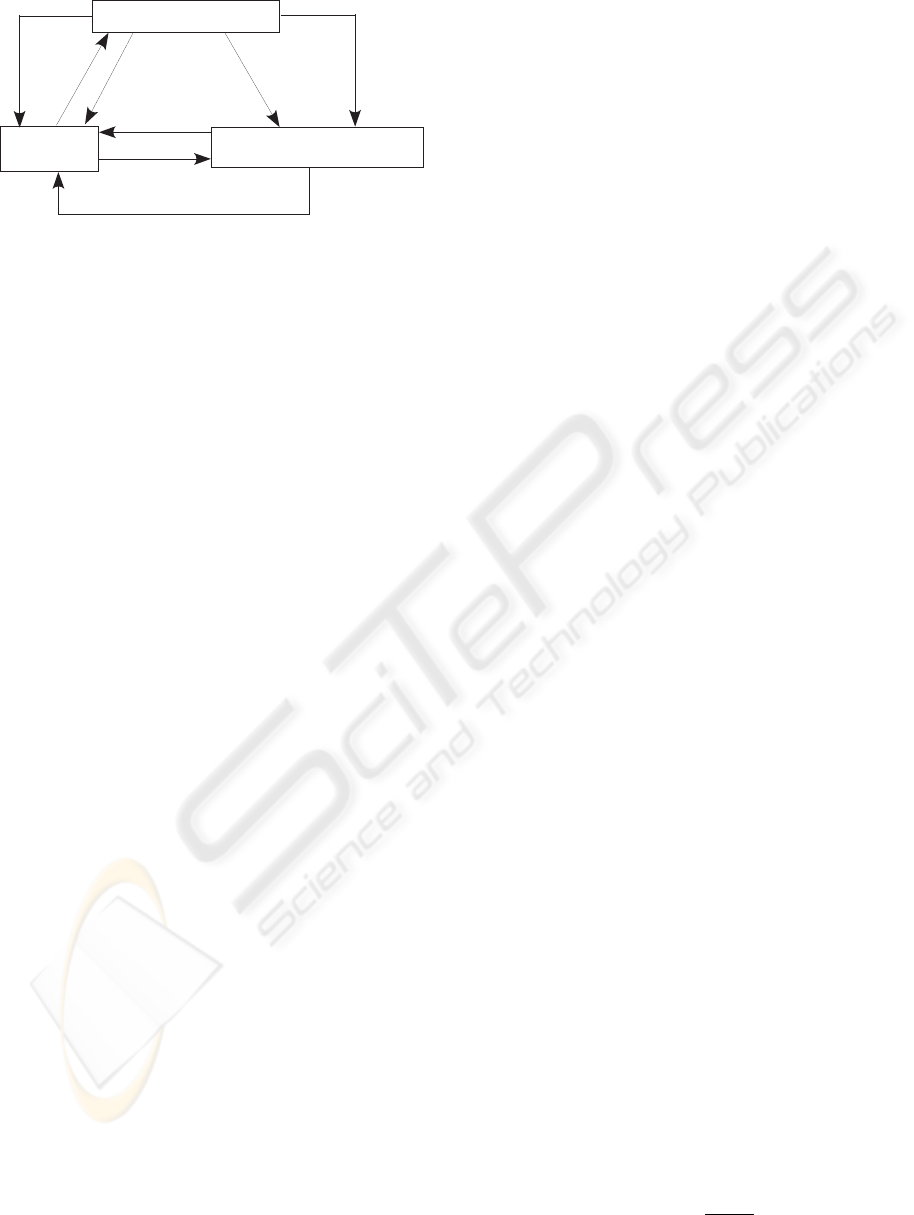
In this article, we implement the elevator group con-
trol problem as BDI multiagent system in Jadex
(Braubach and Pokahr, 2009). Our system consists
of four kinds of agents, a problem management agent
(PMA), an environment agent (EA), a task manage-
ment agent (TMA), and car agents (CAs). Passen-
gers, shafts and cars are instantiated as objects. PMA
defines an elevator group control problem such as the
number of shafts and the number of cars in each shaft.
Then PMA sets up an agent circumstance by calling
EA, TMA, and CAs. EA controls the agent circum-
stance. It creates passengers and informs the situa-
tion of both passengers and cars to TMA. When any
events, such as passengers get off a car, are occurred,
EA updates the circumstance. TMA receives situa-
tions of passengers and cars from EA. When there are
any passengers for whom the car in charge has not
been decided, TMA schedules which car transports
TMA
CA
CA CA CA
EA
passengers
control
create
inform their request
controlcontrolcontrol
assign passengers
The set of agents
The set of objects
Figure 1: Architecture of the Elevator Agent System.
them. Each CA receives the information of passen-
gers that it should serve. Then, CA moves its car in
order to transport its passengers.
2.3 The Environment Agent
The environment agent (EA) controls the agent cir-
cumstance, i.e., it creates passengers as objects,
moves cars according to decision making of CAs and
discards passengers transported to their destination
floors. Each passenger i is treated as an object with
a tuple < t
i
,s
i
,d
i
>. t
i
is the time when i is created.
s
i
and d
i
are the source and destination floors of i, re-
spectively. When i is transported to d
i
at time T , the
service time for i is defined as ST (i) = T − t
i
. Then,
the average efficiency E defined by Eq. (1) is calcu-
lated. IST (i) is the ideal service time for i and it is
defined as the duration that a car moves from s
i
to d
i
without stopping on the way. N is the total number of
passengers. In this article, we define the objective of
the elevator group control problem as minimizing E.
E =
∑
N
i=1
ST (i)
∑
N
i=1
IST (i)
(1)
EA informs the situation of both passengers and
cars to TMA and CAs. According to the informa-
tion, TMA decides which car transports each passen-
ger and each CA selects an action such as up, stop
and down in order to transport their passengers. EA
receives actions selected by CAs and moves cars.
COOPERATIVE LEARNING OF BDI ELEVATOR AGENTS
173

2.4 The Task Management Agent
The task management agent (TMA) decides which car
transports each passenger. Since the policy of TMA
greatly influences E, the designer of an agent system
should design the policy carefully.
One of traditional methods to design the optimal
policy is reinforcement learning. We can construct
the percept spaces as the combination of situations of
cars and passengers. However, it is difficult to acquire
the optimal policy by reinforcement learning, since
the percept space becomes huge. Another method to
design the optimal policy is to use a BDI reasoning
engine. However, it is difficult for the designer to de-
fine inference rules for efficient transportation. That
is, it is difficult to design the optimal policy when we
use either reinforcement learning or a BDI reasoning
engine.
Fortunately, a designer often has some rough
strategies for efficient transportation, such as “the
nearest car from a passenger should transport him.”
In our implementation, we collect a couple of rough
strategies. Then, TMA is designed as a learning
agent, where TMA learns which strategy is useful for
a current situation. The details of learning mechanism
are discussed in Section 3.
2.5 The Car Agents
We designed car agents (CAs) as rational agents,
where each CA can control one car. Five kinds of
plans are implemented for CAs. The list of plans is
shown below.
Go Plan. CA moves its car to a source or destination
floor of passengers.
Call Plan. CA evaluates the nearest source floor of
passengers waiting in an elevator hall.
Board Plan. Passengers take the car.
Transport Plan. CA evaluates the nearest destina-
tion floor of passengers being on board.
Get off Plan. Passengers get off the car.
CAs control their cars by switching these plans.
The Jadex BDI reasoning engine is used for selecting
a plan. Here, we define four inference rules (R1)–
(R4). i, j, k and m indicate passengers. call(i) is a
predicate indicating that the source floor of the pas-
senger i is the nearest from the car. transport(i) in-
dicates that the destination floor of i is the nearest
from the car. board(i) indicates that the car is stop-
ping at the source floor of i and i can board the car.
get o f f (i) indicates that the car is stopping at the des-
tination floor of i. BEL(X) indicates that CA believes
X is true. GOAL(X) indicates that CA has a goal to
make X true. U is the tense operator “until”.
(R1) BEL(call(i)) ⊃
GOAL(call(i)) U (GOAL(transport( j)) ∨
GOAL(board(k)) ∨ GOAL(get o f f (m))
(R2) BEL(transport(i)) ⊃
GOAL(transport(i)) U (GOAL(board( j)) ∨
GOAL(get o f f (k)))
(R3) BEL(board(i)) ⊃
GOAL(board(i)) U GOAL(get o f f ( j))
(R4) BEL(get o f f (i)) ⊃ GOAL(get o f f (i))
These inference rules give the first priority to pas-
sengers who get off the car, the second priority to pas-
sengers who board the car, and the third priority to
passengers who are on board for transported by the
car. The passengers waiting in an elevator hall are
given the lowest priority. When source floors of some
passengers are on the way of the car, however, the car
stops at the floors for the passengers exceptionally.
3 COOPERATIVE
REINFORCEMENT LEARNING
When a passenger resisters his destination floor in the
controller, TMA selects CA that transports the pas-
senger. Then, CA infers a schedule to transport the
passenger. That is, the elevator group control prob-
lem is considered as the problem to find the optimal
policy to assign cars to passengers for minimizing E.
In order to find the optimal policy, we should con-
sider huge kinds of situations. When we try to obtain
the policy by reinforcement learning only by TMA, it
might be difficult to find the optimal policy efficiently.
When we use a BDI reasoning engine for TMA, it is
difficult for the designer to give inference rules induc-
ing the optimal policy. Thus, we introduce coopera-
tive learning of TMA and CAs.
3.1 Framework of Cooperative
Learning
Figure 2 shows the framework of cooperative learn-
ing. The designer of the agent circumstance often has
some rough strategies for efficient transportation. In
our framework, TMA learns which strategy is useful
for a current situation. Reinforcement learning is used
for acquiring the policy of TMA.
When a passenger is created by EA, TMA evalu-
ates the value of each strategy. Each CA also evalu-
ates the value of assigning itself to the passenger on
the basis of reinforcement learning. By using values
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
174
< t
i
,s
i
, d
i
>, S
k
CA
EA
TMA
Plans
Percepts (O
t
)
Percepts (P
t
),
< t
i
,s
i
, d
i
>
Reward(r
i
)
v(O
t
, S
k
)
Assign the passenger i
Reward(r
i
)
Figure 2: Framework of Cooperative Learning.
evaluated by TMA and CAs, TMA selects CA trans-
porting the passenger.
3.2 Learning the Policy of TMA
TMA learns values of strategies for a current situa-
tion. In this article, we gave two strategies to TMA.
S
1
: The nearest car from a passenger should transport
him.
S
2
: The car whose load is the lowest should transport
a passenger.
V (P
t
,S
k
), which is the value of the strategy S
k
for
a current situation P
t
, is evaluated by reinforcement
learning. P
t
= {p
1,t
,...p
M,t
} is a current percept vec-
tor of TMA. p
j,t
is a value of the j-th percept variable
at time t. Now, we assume that TMA assigns CA to
the passenger i at time t on the basis of the strategy S
k
.
We also assume that the car transports the passenger
to his destination floor at time T (> t). Then, V (P
t
,S
k
)
is updated by Eq. (2).
V (P
t
,S
k
) ← V (P
t
,S
k
) + α (r
i
−V (P
t
,S
k
)) (2)
r
i
is a reward defined by IST (i)/ST (i). ST (i) is the
service time for i defined by ST (i) = T − t. IST (i) is
the ideal service time for i. α is a learning ratio.
When TMA assigns CA x to the passenger i, only
the car controlled by x can transport i. When the car
is full, i cannot board the car. In this case, TMA re-
ceives a negative reward r
i
and V (P
t
,S
k
) is updated.
Then, TMA assigns CA to i again. During reinforce-
ment learning, TMA selects a strategy by the epsilon
greedy strategy. When the strategy S
k
is selected,
TMA assigns CA to a passenger only by using S
k
.
3.3 Learning Values by CAs
Each CA learns the value of assigning itself to a pas-
senger, v
x
(O
t
,S
k
). O
t
= {o
1,t
,...o
m,t
} is a current per-
cept vector of CA x at time t. S
k
is the strategy se-
lected by TMA at t. Now, we assume that TMA as-
signs CA x to the passenger i at time t on the basis of
the strategy S
k
. When the car controlled by x trans-
ports the passenger to his destination floor, a positive
reward, r
i
= IST (i)/ST (i), is given to x. Otherwise,
x receives a negative reward. Then, v
x
(O
t
,S
k
) is up-
dated by Eq. (3).
v
x
(O
t
,S
k
) ← v
x
(O
t
,S
k
) + α (r
i
− v
x
(O
t
,S
k
)) (3)
3.4 The Value of a Task Assignment
After trial and error processes (the learning phase)
have been done, TMA acquires which strategy is use-
ful for a current situation and each CA also has the
value of assigning a passenger to it. Then, we can de-
fine the criterion to select a car for a passenger. Equa-
tion (4) defines the value of assigning x to a passenger
at time t. CA x maximizing C(x) is selected as the
most suitable CA for the current situation. In Eq. (4),
K is the number of strategies given by the designer.
C(x) =
K
∑
k=1
V (P
t
,S
k
) v
x
(O
t
,S
k
) (4)
4 SPECIFICATION OF THE
PROBLEM
4.1 Specification
Table 1 shows the specification of our elevator group
control problem. The values of almost parameters are
equal to the values defined in Ref. (The IEICE En-
gineering Sciences Society, Concurrent System Tech-
nology, 2009). The number of cars in a shaft is two in
the reference. When there are multiple cars in a shaft,
it is difficult for us to give inference rules for con-
trolling cars optimally. Thus, we assume that there
is a single car in a shaft. When we can give infer-
ence rules for controlling multiple cars in a shaft, the
proposed framework is applicable to the multi-car el-
evator system. When EA creates a passenger, his ac-
companying persons might be created. In this article,
we call the passenger and his accompanying persons
the passenger group. The number of parsons in a pas-
senger group y is decided on the basis of the Poisson
distribution f (y = n). Equation (5) is the probability
that y = n. λ is 4. The source and destination floors
are decided on the basis of the uniform distribution.
f (y = n) =
e
−λ
λ
n
n!
(5)
COOPERATIVE LEARNING OF BDI ELEVATOR AGENTS
175

Table 1: Specification of the Elevator Group Control Prob-
lem.
The number of floors 30
The number of shafts 4
The number of cars in a shaft 1
The distance between adjacent floors 4 [m]
The maximum speed of a car 6 [m/sec]
The acceleration of a car ±2 [m/sec
2
]
The capacity of a car 20 [persons]
The duration of the simulation 20,000 [secs]
The number of passengers
per minute (before 10,000 secs). 30
The number of passengers
per minute (after 10,000 secs). 34
4.2 Percept Vectors
We assume that TMA can sense two kinds of percepts,
the number of passenger groups towards upper floors
up and the number of passenger groups towards lower
floors down. For efficient reinforcement learning, the
percept values are categorized. Here, we translate the
percept variables up and lower into the categorized
percept variables p
1
and p
2
, respectively. When up ≤
2, p
1
is set to 1. When 2 < up ≤ 5, p
1
is set to 2.
Otherwise, p
1
is set to 3. down is also translated to
p
2
(∈ {1, 2, 3}) in the same manner for up,
CA x can sense three kinds of percepts, the re-
mainder capacity of the car reminder
x
, the distance
between the car and the current passenger distance
x
,
and the load of the car load
x
.
reminder
x
is defined by Eq.(6).
reminder
x
= capacity − (#PW + #PB
x
) (6)
capacity is the capacity of a car. #PW is the number
of persons of the passenger group i that TMA cur-
rently tries to assign to CA. #PB
x
is the number of
passengers in the car controlled by x. Here, we trans-
late the percept variable reminder
x
into the catego-
rized variable o
1
. When reminder
x
≤ 8, o
1
is set to 1.
When 8 < reminder
x
≤ 20, o
1
is set to 2. Otherwise,
o
1
is 3.
distance
x
defined by Eq. (6) is the pseudo dis-
tance between the car controlled by x and the passen-
ger group i.
distance
x
= dist + β #ST
x
(7)
dist is evaluated by using both the situations of the
car and i. Now, we define the situation of the car as
< CF
x
,DF
x
>. CF
x
is the floor that the car is in. DF
x
is
the farthest destination floor of passengers that are in
the car. The situation of i is < t
i
,s
i
,d
i
>. When s
i
is
on the way of the car, i.e., (d
i
− s
i
)(DF
x
−CF
x
) > 0
and (s
i
− CF
x
)(DF
x
− CF
x
) > 0, then dist is evalu-
ated as |s
i
− CF
x
|. Otherwise, dist is evaluated as
|DF
x
−CF
x
| + |DF
x
− s
i
|, since the car should trans-
port all passengers in x before transporting i. #ST
x
is
the predicted number of stops before arriving at the
source floor of i. β is a parameter indicating the cost
of a stop which is defined as 2. The percept vari-
able distance
x
is translated into the categorized vari-
able o
2
. When distance
x
≤ 1, o
2
is set to 1. In the
cases of 1 < distance
x
≤ 10 and 10 < distance
x
≤ 25,
o
2
is set to 2 and 3, respectively. In the cases of
25 < distance
x
≤ 40 and 40 < distance
x
≤ 70, o
2
is
set to 4 and 5, respectively. Otherwise, o
2
is 6.
The third percept variable load
x
indicates the load
of x defined by Eq. (8). N
t
is the number of passen-
ger groups in the circumstance at time t and n
x
is the
number of passenger groups assigned to x. load
x
is
also translated into the categorized variable o
3
. When
load
x
= 0, o
3
is set to 1. When 0 < load
x
≤ 1/6, o
3
is set to 2. When 1/6 < load
x
≤ 1/3, o
3
is set to 3.
Otherwise, o
3
is 4.
load
x
=
n
x
N
t
(8)
5 EXPERIMENTAL RESULTS
5.1 Experimental Setup
Here, we compare four kinds of methods shown be-
low.
S
1
) The nearest car from a passenger should transport
him.
S
2
) The car whose load is the lowest should transport
a passenger.
Learning) TMA switches the strategy according to
the values of strategies S
1
and S
2
.
Cooperative) The proposed method. TMA assigns
passengers to CA on the basis of Eq. (4).
In Learning, TMA does not evaluate C(x). That is,
Learning does not use v
x
(O
t
,S
k
) for car assignment.
α in Eqs. (2) and (3) is 0.8. ε for the epsilon
greedy strategy is 0.2. A negative reward is defined
as −0.1. These parameter values are decided by per-
forming preliminary experiments.
5.2 Results
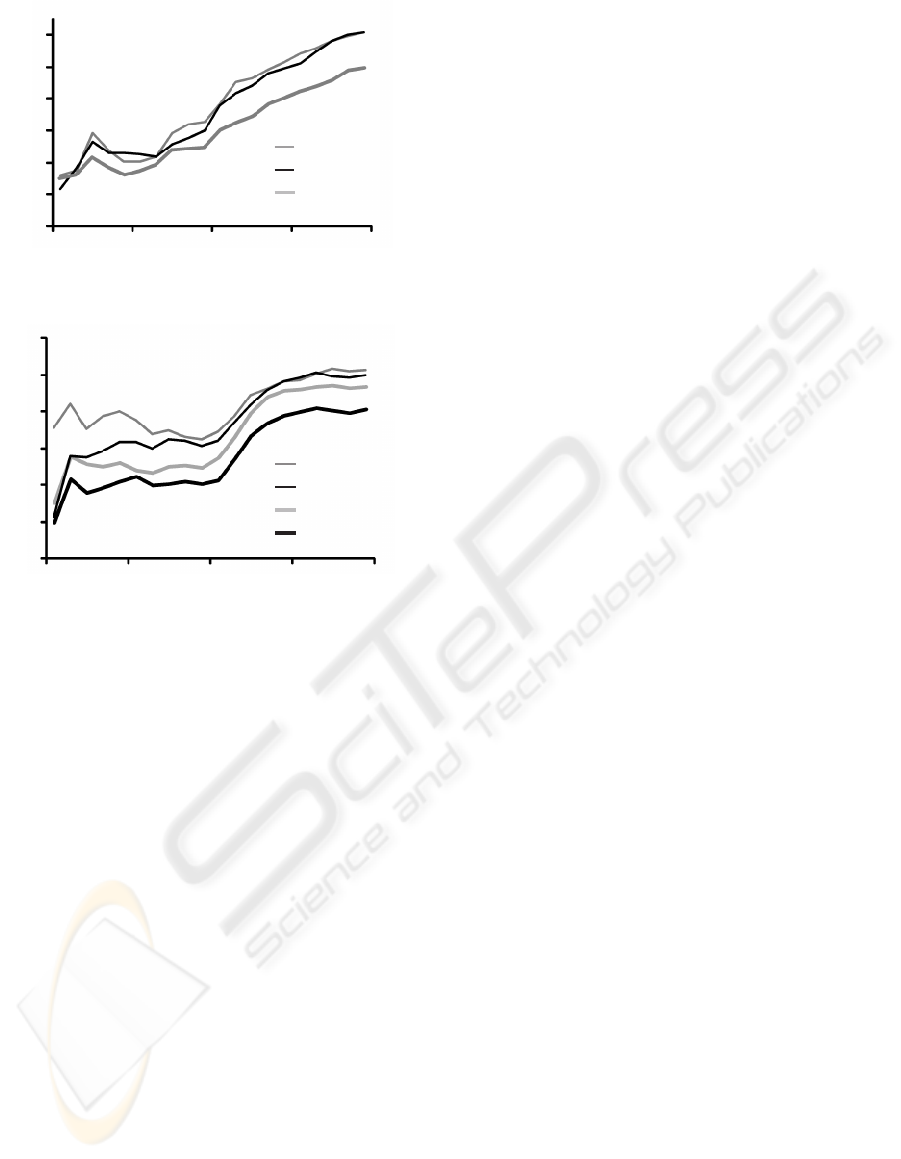
Figure 3 shows the changes of the objective func-
tion E during the learning phase. Since Learning and
Cooperative are equivalent in the the learning phase,
results for Cooperative are omitted. In Fig. 3, E for
Learning is the lowest. Thus, the policy for switching
strategies has been acquired well.
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
176
Learning
S
2
S
1
E
t
3.2
2.0
2.4
2.8
0 5,000 10,000 15,000 20,000
Figure 3: Changes of E during the learning phase.
E
t
3.2
2.0
2.4
2.8
0 5,000 10,000 15,000 20,000
Learning
S
2
Cooperation
S
1
Figure 4: Results of cooperative assignment.
Figure 4 shows the results of cooperative assign-
ment. Here, we use a passenger sequence that is dif-
ferent from the sequence used in the previous experi-
ment. Cooperative assigns a passenger to CA by us-
ing Eq. (4). In Learning, the optimal strategy is se-
lected according to V (P
t
,S
k
). When a passenger se-
quence is changed, Learning is more efficient than
S
1
and S
2
. E for Cooperative is lowest of all. That
is, V (P
t
,S
k
) and v
x
(O
t
,S
k
) are acquired adequately by
reinforcement learning, and C(x) is a good criterion
for efficient assignment of a car.
6 CONCLUSIONS
We have proposed a cooperative reinforcement learn-
ing method for rational agents, and the method have
been applied to the elevator group control problem.
Experiment results show that the proposed method ac-
quires better rules than the methods without coopera-
tive learning.
In this article, however, we have not applied our
method to a multi-car elevator system and percept
variables such as reminder
x
are discretized manually.
Improvement of our method to overcome these prob-
lems is remained as our future works.
ACKNOWLEDGEMENTS
The authors would like to thank the anonymous re-
viewers for their valuable comments.
REFERENCES
Braubach, L. and Pokahr, A. (accessed 11 August, 2009).
Jadex BDI agent system – overview.
http://vsis-www.informatik.uni-
hamburg.de/projects/jadex/.
Doniec, A., Espi
´
e, S., Mandiau, R., and Piechowiak, S.
(2006). Non-normative behaviour in multi-agent sys-
tem: Some experiments in traffic simulation. In Pro-
ceedings of IAT2006, pages 30–36.
Excelente-Toledo, C. B. and Jennings, N. R. (2003). Learn-
ing when and how to coordinate. Web Intelligence and
Agent Systems, IOS Press, 1(3-4):203–218.
Ikeda, K., Suzuki, H., Kita, H., and Markin, S. (2008).
Exemplar-based control of multi-car elevators and
its multi-objective optimization using genetic algo-
rithm. In The 23rd International Technical Confer-
ence on Circuits/Systems, Computers and Communi-
cations, pages 701–704.
Katagiri, H., Hirakawa, K., and Hu, J. (2000). Genetic net-
work programming - application to intelligent agents
-. In Proceedings of SMC2000, pages 3829–3834.
Rao, A. S. and Georgeff, M. P. (1991). Modeling rational
agents within a BDI-architecture. In Proceedings of
KR’91, pages 473–484.
Sutton, R. S. and Barto, A. G. (1998). Reinforcement Learn-
ing. The MIT Press.
The IEICE Engineering Sciences Society, Concurrent Sys-
tem Technology (accessed 11 August, 2009). CST so-
lution competition 2008.
http://www.ieice.org/ cst/compe08/. (in Japanese).
The RoboCup Federation (accessed 11 August, 2009).
http://www.robocup.org/.
Valdivielso, A., Miyamoto, T., and Kumagai, S. (2008).
Multi-car elevator group control: Schedule comple-
tion time optimization algorithm with synchronized
schedule direction and service zone coverage oriented
parking strategies. In The 23rd International Techni-
cal Conference on Circuits/Systems, Computers and
Communications, pages 689 – 692.
COOPERATIVE LEARNING OF BDI ELEVATOR AGENTS
177
