
OBSERVATION WITH BOUNDS OF BIOLOGICAL SYSTEMS
A Linear Programming Approach
Fernando Tadeo and Mustapha Ait Rami
Dpto. Ingenieria de Sistemas y Automatica, Universidad de Valladolid, 47005 Valladolid, Spain
Keywords:
Compartmental models, Observers, Linear Programming, Kinetic models.
Abstract:
This paper presents a technique to estimate the states of biological systems that cannot be directly measured,
by using available measurements of other states that affect them. More precisely, the proposed technique
makes it possible to derive, at each moment, the possible range of variation of these unmeasured states. It is
based on having a compartmental model of the system (which might include uncertain parameters), and then
solving a Linear Programming problem. A practical example, based on the kinetic model of drug distribution
through the human body, is provided to show its applicability.
1 INTRODUCTION
It is well known that most biological systems can be
represented mathematically in quite a precise way by
compartmental models (Jacquez, 1985). The main
characteristic of these compartmental systems is that
that the internal states are nonnegative by nature, as
they represent concentrations, temperatures, cell birth
or losses, etc: See (Hynne et al., 2001; Luzyanina
et al., 2007; Linninger et al, 2009) and references
therein for many practical examples.
Thus, this paper considers the compartmental ob-
servation problem, which consists of constructing
compartmental observers (Vanden Hof, 1998), that is,
observers that ensure the compartmental properties of
the states (i.e., positivity and conservation). These ob-
servers are very important in biological systems: stan-
dard observers and filters provided by systems theory
(Luenberger, 1966; Gover and Brown, 1992), if they
are not designed taking into account the characteris-
tics of compartmental systems, might give some neg-
ative values, which are completely illogical (those ob-
servers might, for example, estimate that certain con-
centrations are negative). The method presented here,
which circumvents this problem, is based on some re-
cent results on the theory of positive observers (Ait
Rami et al, 2007a; Ait Rami et al., 2007b), which can
be applied to compartmental models. These results
are used here to provide conditions for the observa-
tion of biological systems described by compartmen-
tal models, providing a simple approach to numeri-
cally address the determination of compartmental ob-
servers (as linear programs can be solved easily using
off-the-shelf software).
Moreover, the proposed compartmental observers
can be used to obtain tight upper and lower bounds on
the estimated variables, even in the presence of uncer-
tain parameters in the model. That is, if bounds on the
initial states of the observed system are known, and
uncertainty in the system matrices can be evaluated,
which is common in practice, the evolution of the un-
measured states will always be between the estimated
bounds, providing a bounding observer. Moreover,
these estimated bounds converge to the real value,
and, compared to previous approaches for bounding
observers (Gouze et al., 2000; Rapaport, 2005; Alamo
et al, 2005), the proposed observer is simple to im-
plement, and the design of the observer parameters
is based on straightforward conditions (this design is
based on solving simple Linear Programming condi-
tions).
The proposed approach is directly applicable to
many systems in biology (including medicine), such
as those in (Hynne et al., 2001; Luzyanina et al., 2007;
Linninger et al, 2009). As an example, the kinetic
models of the bone-seeking radiopharmaceutical Tc-
99m(Sn)methylenediphosphonate (Tc-MDP) in adult
humans, that were derived in (Makler and Charkes,
1980), are used here to present the problem, and show
that, by using the proposed approach, it is possible
to provide tight estimations of the unmeasured states,
giving upper and lower bounds on the real states.
The paper is organized as follows: Section 2
presents the example that will be used as case study,
230
Tadeo F. and Ait Rami M. (2010).
OBSERVATION WITH BOUNDS OF BIOLOGICAL SYSTEMS - A Linear Programming Approach.
In Proceedings of the Third International Conference on Bio-inspired Systems and Signal Processing, pages 230-235
DOI: 10.5220/0002717602300235
Copyright
c
SciTePress

Section 3 gives the structure of the proposed bound-
ing observer and a methodology to select the observer
parameters. Finally, Section 4 presents a complete ap-
plication to the case study, and some conclusions are
given.
2 MOTIVATING EXAMPLE
An example is now given to show the kind of prob-
lems we want to solve: Kinetic models are frequently
used to determine doses of drugs in radiotherapy. For
instance, the short-lived bone-seeking radiopharma-
ceutical
99m
Tc-methylene diphosphonate (Tc-MDP)
is used in bone imaging for investigating the state
of the skeleton in diffuse metabolic bone diseases
(osteoporosis, hyperparathyroidism) or at local ab-
normalities in metastatic bone disease (Blake et al.,
2002). Based on clinical measurements in adult hu-
mans, the portion of the administered dose of Tc-
MDP in some compartments of the human body was
determined (Makler and Charkes, 1980) to be pre-
cisely given by the following compartmental model:
dx
dt
=
-k
21
− k
41
− k
51
k
12
0 k
14
k
15
k
21
-k
12
-k
32
k
23
0 0
0 k
32
-k
23
0 0
k
41
0 0 -k
14
0
k
51
0 0 0 -k
15
x(t),
y(t) =
c 0 0 0 0
x(t).
(1)
where the vector x(t) contains the states, that cor-
respond to the portion of the dose of the Tc-MDP
tracer in the different compartments: x
1
(t) is the por-
tion of the dose in the blood, x
2
(t) in the bone-ECF,
x
3
(t) in normal bone, x
5
(t) in the tubular urine and
x
4
(t) in the rest of the human body. Some values for
the parameters of the model were obtained from phys-
iological data. Our objective is to provide a technique
that uses this mathematical model and the available
information on the parameters to design an observer
that gives time-dependent upper and lower bounds on
the portions in the different compartments. The esti-
mations will be continuously updated based on mea-
surements of the dose in the blood just after an in-
jection (this is the only measurement that is assumed
here to be available, but the technique can be directly
extended to other measurements).
Model (1) corresponds to the general class of pos-
itive (compartmental) systems described by
dx
dt
= Ax(t), y(t) = Cx(t), x(0) ≥ 0. (2)
It is well known (Luenberger, 1966) that the ob-
servation of the states of dynamical systems described
by (2)) can be based on using a classical Luenberger
observer, that consists of integrating the linear differ-
ential equations, starting from adequate initial condi-
tions, of the following dynamical system:
dΘ
dt
= (A− LC)Θ(t) + Ly(t).
(3)
The observer design is then based on selecting a ma-
trix L that gives closed-loop stability and some per-
formance. This design is frequently based on placing
the eigenvalues of the matrix A− LC in desired posi-
tions. Once L is selected, it is only necessary to in-
tegrate (3), starting from adequate initial conditions,
to get estimations that converge to the real state: this
simplicity of concept and implementation has made
Luenberger observers useful for those practical appli-
cations where the system can be precisely described
by a dynamical system.
Unfortunately, the Luenberger observer in (3)
does not take into account the fact that the system
(2) is compartmental, so unrealistic results might be
(temporarily) obtained for some of the states.
Moreover, in many applications, it is important to
ensure upper and/or lower bounds on the real states,
but standard Luenberger observers do not ensure that
the estimated states converge from above (or from be-
low) to the real states.
Another problem of classical observers is that the
uncertainty in the system parameters or the initial
state cannot be easily incorporated into the observer:
For example, clinical trials detected a variation be-
tween individuals between 0.502 and 0.578 for k
12
,
whereas k
32
was found to vary between 1.018 and
1.092. Methodologies to include this information
for designing the observer are available but are quite
complex (Gouze et al., 2000; Combastel, 2005; Rapa-
port, 2005). Our objectiveis to give a general method-
ology that is simple to apply and does not need in-
volved calculations.
Thus, this paper concentrates on providing a prac-
tical methodology to estimate states for biological
systems, that can be described by (2), which ensures
that the estimated states are logical (i.e., never nega-
tive), provide tight bounds on the estimated variables,
and takes into account uncertain parameters. This
proposed methodology is described in the next sec-
tion.
OBSERVATIONWITH BOUNDS OF BIOLOGICAL SYSTEMS - A Linear Programming Approach
231

3 PROPOSED BOUNDING
OBSERVER
We assume that the system whose states are to be es-
timated on-line can be described as a compartmen-
tal system (maybe including uncertain parameters),
where there are p measured variables (that form the
column vector y(t)) and n internal states (that describe
each compartment, and form the state vector x(t)).
More precisely, we consider models that can be de-
scribed by the following linear dynamical model:
˙x(t) = Ax(t), y(t) = Cx(t), x(0) ≥ 0 (4)
Thus, the square constant matrix A is composed of
n × n elements (that will be denoted by a
ij
), and the
constant matrix C has n rows and p columns of el-
ements denoted by c
ij
. These matrices are assumed
to be uncertain, but they can be bounded by known
matrices A, A, C and C, such that
A ≤ A ≤ A and C ≤ C ≤ C. (5)
Mathematically, system (4) is said to be compartmen-
tal if the matrix A does not have negative off-diagonal
elements (it is called a Metzler matrix) and satisfies
the following property:
n
∑
i=1
a
ij
≤ 0. (6)
It is assumed that bounds on the initial state are
known: x ≤ x(0) ≤ x. In the uncertain case A does
not have negative off- diagonal elements, but A and
A probably do not fulfill the property (6): they pro-
vide a positive system, but probably not a compart-
mental one. As has been discussed in Section 2, clas-
sical observers are not adequate for compartmental
systems, specially in the presence of uncertainty in
the parameters of the system. Thus, we propose to
incorporate to the observer the available information
on the system uncertainties, by using an observer that
gives upper and lower bounds on the real states. This
makes it possible to incorporate uncertainty into the
initial states of the system, as they are never perfectly
known. The proposed approach is based on using an
observer with two independent sets of states: one set
(denoted Θ) is used to derive an upper bound on the
real state, whereas the other set (Θ) makes it possible
to derive a lower bound.
The proposed observer is then given by the fol-
lowing two independent dynamical equations:
dΘ
dt
= (A− LC)Θ(t) + Ly(t),
dΘ
dt
= (A− LC)Θ(t) + Ly(t).
(7)
The states are then estimated by integrating (7), start-
ing from adequate initial conditions. The design is
then based on estimating an observer gain L which
ensures that
1) both sets of dynamical equations in (7) are stable,
2) the integration of the dynamical equations evolve
towards the real state,
3) the states are always between Θ(t) and Θ(t)
4) the lower bound Θ(t) is always nonnegative, pro-
vided that the initial condition is nonnegative.
To characterize the set of observer gains that fulfill
these properties the following condition is proposed
(based on the results in (Ait Rami et al., 2007b)):
There exists a bounding observer of system (4) of the
form (7) if and only if the following Linear Program
has a solution:
A
T
λ−C
T
∑
n
i=1
z
i
< 0,
c
T
i
z
j
≥ 0 for i, j = 1, . . . , n,
a
ji
λ
j
− c
T
i
z
j
≥ 0 for i 6= j,
λ > 0.
(8)
The variables of this Linear Programming prob-
lem are λ = [λ
1
. . . λ
n
]
T
∈ R
n
and z
1
, . . . , z
n
∈ R
r
,
whereas L can be obtained from any feasible solution
of this LP problem:
L =
1
λ
1
z
1
1
λ
2
z
2
...
1
λ
n
z
n
. (9)
To clarify the notation, a
ij
are the elements of the ma-
trix A, c
i
are the columns of C, etc. It must be pointed
out that the proposed approach can be extended to re-
lated problems, such as compartmental systems with
delays (Ait Rami et al., 2007b), discrete-time systems
(Ait Rami et al, 2007a), disturbances, etc.
4 APPLICATION TO THE
EXAMPLE
Based on clinical measurements (Makler and
Charkes, 1980) obtained the following parameters
for the compartmental model (1), including vari-
ability in the parameters: k
12
= 0.540 ± 0.038,
k
21
= 0.095 ± 0.003, k
14
= 0.277 ± 0.007,
k
41
= 0.431 ± 0.011, k
15
= 0.233, k
51
= 0.024,
k
23
= 0.049 ± 0.001, and k
32
= 1.055 ± 0.037. To
take into account the unavoidable measurement errors
we fix c = 1± 0.05.
BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing
232

Based on the result presented in the previous sec-
tion, the Linear Programming problem (3) can be eas-
ily solved to obtain a compartmental observer with the
following observer gain:
L =
12 0.0365 0.005 0.335 0.024
. (10)
It is now shown how the compartmental observer (7),
with this gain, can be used to provide upper and lower
bounds on the estimated states, taking also into ac-
count the unavoidable uncertainty in the system pa-
rameters and initial conditions.
For simulation, assume that the concentration in
the blood is continuously measured, shortly after in-
jection, so the conditions of the system when the
observation starts are bounded within the following
range:
y(0) − 0.05
0
0
0
0
≤ x(0) ≤
y(0) + 0.05
0.2
0.3
0.6
0.04
. (11)
with y(0) the first measurement of the dose in blood.
Thus, to get a bounding observer, the initial
condition of the lower observer states is Θ(0) =
y(0) − 0.05 0 0 0 0
T
, whereas the initial
condition of the upper observer states is Θ(0) =
y(0) + 0.05 0.2 0.3 0.6 0.04
T
. By the re-
sult in Section 3, the evolution of the state x(t) will
always be between the estimated states Θ(t) ≥ 0 and
Θ(t). Moreover,these estimations converge to the real
value, and are always nonnegative.
These claims can be confirmed in Figures 1 to
5, which plot the state evolutions for the parame-
ters obtained for one of the patients in the origi-
nal study, starting from the initial conditions (x(0) =
0.5 0.05 0.15 0.4 0.01
T
), when the dos-
ing has finished (i.e., with null input), together with
the bounds estimated using the approach proposed
in Section 3 and the gain (11). For simplicity, it is
assumed that the system parameters remain constant
throughout the experiment (the plant parameters cor-
respond to mean values) and there is no measurement
noise. It is possible to see that the estimated states are
nonnegative and converge to the real values, giving
lower and upper bounds on the real states that con-
verge to the real values.
Thus, for example, using the proposed approach,
it is possible to give tight estimations of the concen-
tration of in the bone-ECF (see Figure 2), despite the
uncertain initial conditions, and the person-to-person
variations in the nominal parameters: for example, in
Figure 2, it is possible to see that just two minutes
after the start of measurements of the concentration
of Tc-MDP in the blood it is possible to predict pre-
cisely that the portion of dose in the bone-ECF will be
greater than 0.022 and smaller than 0.037, whereas for
the non-bone-ECF ten minutes are enough to estimate
the portion of dose with a 10% accuracy.
These estimations can be easily used to derive the
figures of merits usually used to derive imaging times.
In this case, the objective is to distinguish, in the im-
ages, the bone from the surrounding tissue, so, fol-
lowing common practice, we define the target to be
Q
T
= 0.1x
1
+ x
2
+ x
3
, (assuming a 10% of blood vol-
ume in the skeleton), whereas the background is pro-
vided to be Q
B
= 0.9x
1
+ x
4
. This makes it possible
to easily derive bounds on figures of merits frequently
used, such as the contrast, shown in Figure 6:
Contrast =
C
T
C
B
, (12)
or the relative contribution of target and background,
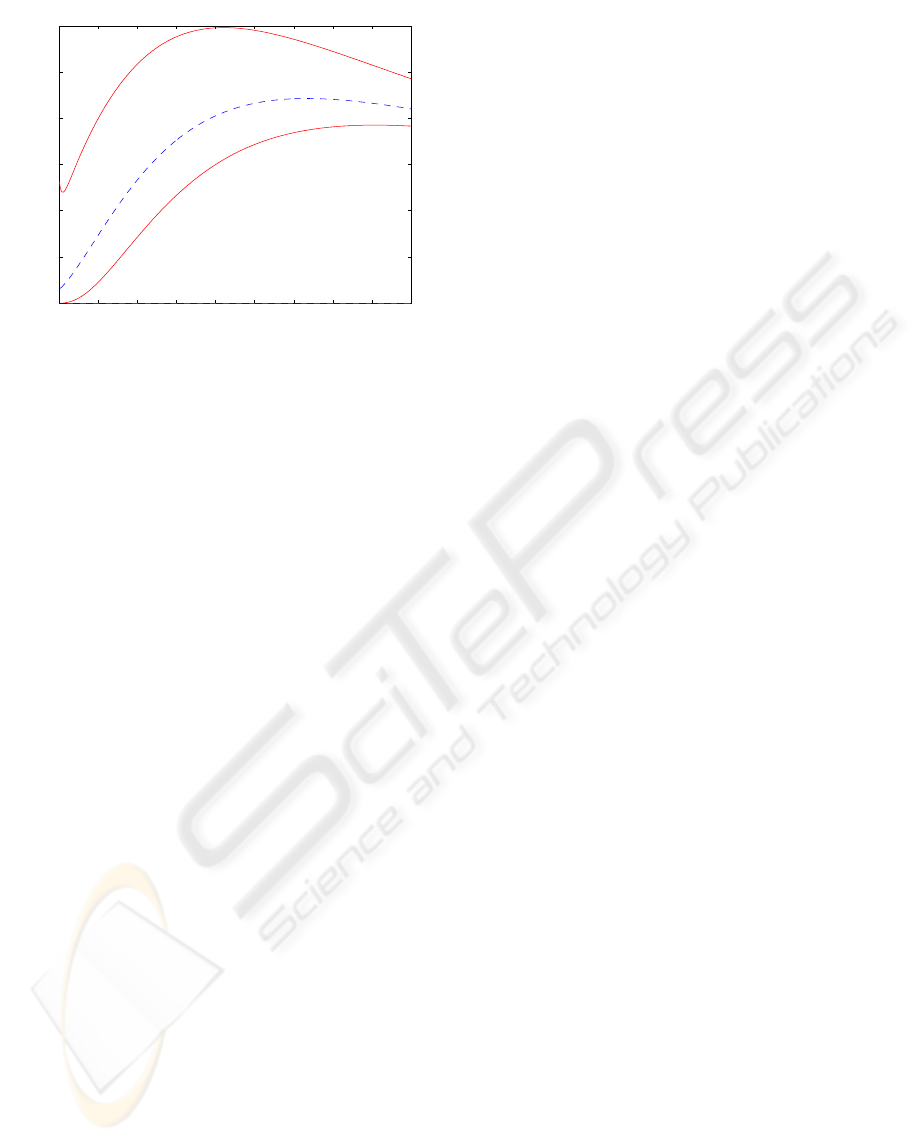
depicted in Figure 7, which statistically corresponds
to the Beck-Harper figure of merit:
Q =
(C
T
−C
B
)
2
C
T
+C
B
. (13)
The obtained results agree with those obtained in
practice (Subramanian et al., 1975; Rosenthall et al.,
1997; Fogelman et al, 1979).
We must point out that parallel results can be ob-
tained when dosing is measured in the urine, maybe
simultaneously with measurement in the blood, fol-
lowing the same procedure, and it is directly applica-
ble to other tracers used in medical imaging, such as
18
F-Fluoride (Cook et al., 2000). Moreover, the pro-
posed methodology is general, as the only property
used is the fact that the system can be described as a
compartmental model with uncertainty (which is the
case of most biological systems (Jacquez, 1985)).
5 CONCLUSIONS
This paper has proposed a new approach to solve the
observation problem for compartmental models in bi-
ology, by providing upper and lower bounds on the
unmeasured states, which incorporates uncertainty in
the parameters and initial conditions of the system.
This problem has been studied, and a simple nec-
essary and sufficient condition for its solvability has
been proposed, based on solving a Linear Program-
ming Problem. An illustrative case study, based on a
radiopharmaceuticalproblem, shows the feasibility of
the proposed approach, and how it can be used to de-
rive upper and lower bounds on the estimated states.
OBSERVATIONWITH BOUNDS OF BIOLOGICAL SYSTEMS - A Linear Programming Approach
233

0 10 20 30 40 50 60
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
State 1, with bounds given by the proposed observer
−
[1]
O
x[1]
−[1]
O
t (minutes)
Portion of dose
Figure 1: Evolution of the concentration in the blood, and
estimated bounds.
0 10 20 30 40 50 60
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
State 2, with bounds given by the proposed observer
−[2]
O
x[2]
−[2]
O
t (minutes)
Portion of dose
Figure 2: Evolution of the concentration in the bone-ECF,
and estimated bounds.
0 10 20 30 40 50 60
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
State 3, with bounds given by the proposed observer
−
[3]
O
x[3]
−[3]
O
t (minutes)
Portion of dose
Figure 3: Evolution of the concentration in the bone, and
estimated bounds.
0 10 20 30 40 50 60
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
State 4, with bounds given by the proposed observer
−
[4]
O
x[4]
−[4]
O
t (minutes)
Portion of dose
Figure 4: Evolution of the concentration in the non-bone-
ECF, and estimated bounds.
0 10 20 30 40 50 60
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
State 5, with bounds given by the proposed observer
−[5]
O
x[5]
−[5]
O
t (minutes)
Portion of dose
Figure 5: Evolution of the concentration in the urine, and
estimated bounds.
0 10 20 30 40 50 60 70 80 90
0
1
2
3
4
5
6
7
8
9
Contrast: estimated worst−case bounds
t(min)
%uncorrected dose (uncorrected)
Figure 6: Contrast, with estimated bounds.
BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing
234
0 10 20 30 40 50 60 70 80 90
0
1
2
3
4
5
6
Quality Q=target/background
t(min)
%uncorrected dose (uncorrected)
Figure 7: Figure of merit Q with estimated bounds.
Further work is being carried out to include the
effect of measurement noise, and applying the pro-
posed technique to complicated problems in biology
(including the presence of time-varying delays).
This work has been funded by MiCInn DPI2007-
66718-C04-02 and a ”Ram´on y Cajal” grant.
REFERENCES
Ait Rami, M., Helmke, U., Tadeo, F. Positive Observation
Problem For Linear Time-Lag Positive Systems IFAC
Workshop on Systems, Structure and Control, Foz de
Iguazu, Brazil, 2007.
Ait Rami, M., Helmke, U., Tadeo, F. Positive observation
problem for time-delays linear positive systems. IEEE
Mediterranean Control Conference, Greece, 2007.
Alamo, T., Bravo, J.M., Camacho, E.F., Guaranteed state
estimation by zonotopes, Automatica, 41(6): 1035-
1043, 2005.
Blake, G.M., Park-Holohan, S.-J., Fogelman, I., Quantita-
tive Studies of Bone in Postmenopausal Women Using
18
F-Fluoride and
99m
Tc-Methylene Diphosphonate. J
of Nuclear Medicine, 43:338-345.
Combastel, C.. A state bounding observer for uncertain non-
linear continuous-time systems based on zonotopes.
44th IEEE CDC, Seville, 2005.
Cook, G.J.R., Lodge, M.A., Blake, G.M., Marsden, Pl.K.,
Fogelman, I. Differences in skeletal kinetics between
vertebral and humeral bone measured by
18
F-Fluoride
positron emission tomography in postmenopausal
women. J Bone Mineralization Research 15:763-769,
2000.
Fogelman, I., Citrin, D.L., McKillop, J.H. et al., A clini-
cal comparison of Tc-99m HEDP and Tc-99m MDP
in the detection of bone metastases. J of Nuclear
Medicine 20: 98-101, 1979.
Gouze, J.L., Rapaport, A., Hadj-Sadok, Z.M.. Interval ob-
servers for uncertain biological systems. J of Ecologi-
cal Modelling, 133:4556, 2000.
Gover, R., Hwang, P.Y.C., Introduction to Random Signals
and Applied Kalman Filtering. John Wiley & Sons,
1997.
Hynne, F., Dano, S., Sorensen, P.G., Full-scale model of
glycolysis in Saccharomyces cerevisiae. Biophysical
Chemistry, 94: 12116, 2001.
Jacquez, J.A., Compartmental Analysis in Biology and
Medicine. Ann Arbor, MI: University of Michigan
Press, 1985.
Linninger, A.A., Xenos, M., Sweetman, B., Ponkshe, S.,
Guo, X., Penn, R. A mathematical model of blood,
cerebrospinal fluid and brain dynamics. J of Mathe-
matical Biology, 59(6): 729-759, 2009.
Luenberger, D.G., An introduction to observers. IEEE
Trans. Aut. Control, 16: 596–602, 1966.
Luzyanina, T., Mrusek, S., Edwards, J.T., Roose, D., Ehl,
S., Bocharov, G., Computational analysis of CFSE
proliferation assay. J of Mathematical Biology 54(1):
57-89, 2007.
Makler, P.T., Charkes, N.D. Studies of Skeletal Tracer
Kinetics IV. Optimum Time Delay for Tc-99m(Sn)
Methylene Disphosphonate Bone Imaging, J of Nu-
clear Medicine, 21: 641-645, 1980.
Rapaport, A., Dochain, D., Interval observers for bio-
chemical processes with uncertain kinetics and inputs,
Mathematical Biosciences, 193(2) 235-253, 2005.
Rosenthall, L., Arzoumanian, A., Lisbona, R., et al., A lon-
gitudinal comparison of the kinetics of
99m
Tc-MDP
and
99m
Tc-EHDP in humans, Clin. Nucl. Med, 2:
232-234, 1997.
Subramanian, G., McAfee, J.G., Blair R.J. et al., An
evaluation of
99m
Tc-labeled phosphate compounds
as bone imaging agents, Radiopharmaceuticals, 319-
328, 1975.
Van Den Hof, J.M., Positive linear observers for linear
compartmental systems. SIAM J on Control and Op-
timization, 36: 590–608, 1998.
OBSERVATIONWITH BOUNDS OF BIOLOGICAL SYSTEMS - A Linear Programming Approach
235
