PREDICTING TRAFFIC FLOW IN ROAD NETWORKS

Using Bayesian Networks with Data from an Optimal Plate Scanning Device

Location

S. S´anchez-Cambronero, A. Rivas, I. Gallego and J. M. Men´endez

Department of Civil Engineering, University of Castilla-La Mancha, 13071 Ciudad Real, Spain

Keywords:

Trafﬁc data updating, Gaussian Bayesian networks, Probability intervals, Plate scanning, RMARE.

Abstract:

This paper deals with the problem of predicting route ﬂows (and hence, Origin-Destination (OD) pair and

link ﬂows) and updating these predictions when plate scanned information becomes available. To this end,

a normal Bayesian network is built which is able to deal with the joint distribution of route and link ﬂows

and the ﬂows associated with all possible combinations of scanned link ﬂows and associated random errors.

The Bayesian network provides the joint density of route ﬂows conditioned on the observations, which allow

us not only the independent or joint predictions of route ﬂows, but also probability intervals or regions to be

obtained. A procedure is also given to select the subset of links to be observed in an optimal way. An example

of application illustrate the proposed methodology and shows its practical applicability and performance.

1 INTRODUCTION

As is well known, in trafﬁc problems several types of

ﬂows can be considered, such us route, OD-pair, link

and node ﬂows, but other types are also possible in-

cluding disaggregated versions of ﬂows, as OD-pair

ﬂows through a given link or node and with a given

origin and/or destination, etc. In this paper, we aim

at estimating route ﬂows, because once they are es-

timated, other trafﬁc ﬂows such as OD-pair and link

ﬂows can be immediately calculated from the corre-

sponding incidence matrices. We also deal with an-

other type of ﬂow, which corresponds to ﬂows pass-

ing only through a given subset of links. This is the

natural type of ﬂow for the plate scanning technique.

In the trafﬁc literature, several problems related to

these types of trafﬁc ﬂows were studied, such as trip

matrix estimation (ME) or trafﬁc assignment prob-

lems. The assignment model has as inputs the OD

pair ﬂows and produces as outputs the probabilities of

a traveler to select the different routes of an OD pair

(see (Castillo et al., 2008c) for deterministic models

and (Praskher and Bekhor, 2004) for stochastic mod-

els). On the contrary, the ME problem has as inputs

these probabilities and link ﬂows and produces as out-

puts the OD pair ﬂows. However, these two problems

are closely connected and some inconsistencies can

occur in the trafﬁc estimation if they are solved sep-

arately. To solve this problem, they can be combined

into one problem, in which the trip matrix ﬂow esti-

mation and the trafﬁc assignment problems become a

single one. Several techniques have been proposed to

solve this combined problem, which include, the well

known bi-levelapproaches (see (Conejo et al., 2006)).

In the ME problem one tries to estimate origin-

destinations (OD) trip matrices based on some ob-

served link ﬂows. Unfortunately, this is an under-

speciﬁed problem, due to the fact that the number of

paths between OD pairs is normally much larger than

the number of observed links (i.e. the incidence ma-

trix is not full rank), and there are inﬁnitely many so-

lutions satisfying the conservation laws. In order to

have a unique solution, one has to provide more in-

formation by means of a prior OD trip matrix, which

can come from many different sources, including an

out-of-date, subjectively-guessed, or obtained by an

alternative method, etc. Based on the observations

(OD or link ﬂows) and this prior OD matrix, the OD

matrix can be estimated by many different methods,

such as the least squares and the generalized least

squares methods ((Doblas and Benitez, 2005)), the

entropy or information based methods ((Van Zuylen

and Willumsen, 1980)), and statistical based meth-

ods (see (Cascetta and Nguyen, 1988), for classi-

cal approaches, and (Tebaldi and West, 1996) for

the Bayesian approaches). Some other works used

552

Sánchez-Cambronero S., Rivas A., Gallego I. and M. Menéndez J. (2010).

PREDICTING TRAFFIC FLOWIN ROAD NETWORKS - Using Bayesian Networks with Data from an Optimal Plate Scanning Device Location.

In Proceedings of the 2nd International Conference on Agents and Artiﬁcial Intelligence - Artiﬁcial Intelligence, pages 552-559

DOI: 10.5220/0002717705520559

 SciTePress

Bayesian networks such as (Sun et al., 2006) and

(Castillo et al., 2008b).

In this paper we have used the plate scanning tech-

nique in order to deal with the problems exposed

above: the under-speciﬁcation on one hand, and the

inconsistences between OD matrix estimation and the

assignment problems on the other (see (Castillo et al.,

2008a)). The idea is to register the plate numbers of

the circulating vehicles together with the correspond-

ing times at some subsets of links and use this in-

formation to reconstruct vehicle routes. The plate

scanning approach to trafﬁc ﬂow estimation and re-

construction has been revealed as a very promising

alternative to other existing methods based on link

ﬂows or trafﬁc surveys, as was done in other standard

methods, because it provides much richer informa-

tion about trafﬁc ﬂows than simply observing (count-

ing) link ﬂows (see (Watling, 1994) or (Castillo et al.,

2008a)).

The new contribution of this paper consists of pre-

senting a Bayesian network to estimate route ﬂow

based on plate scanning. It combines two recently de-

veloped techniques, Bayesian network and plate scan-

ning, to predict trafﬁc ﬂows. Using both thechniques,

the random dependence structure of trafﬁc ﬂows in-

cluding not only OD-pair and link ﬂows but route

ﬂows and ﬂows associated with subsets of links are

provided. In addition, a procedure is also given to se-

lect the subset of links to be observed in an optimal

way subject to a given budget.

The paper is organized as follows. In section 2 the

problem of selecting an optimal subset of links to be

scanned is dealt with. Section 3 introduces Bayesian

networks and describes the proposed model for route

ﬂow estimation. In Section 4 a example of applica-

tions is used to illustrate the effectiveness of the pro-

posed model and clarify some of its implementation

details. Finally, Section 5 provides some conclusions.

2 THE PLATE SCANNING

DEVICE LOCATION PROBLEM

In real life, the true error or reliability of an esti-

mated O D matrix is unknown. (Yang et al., 1991)

proposed the concept of maximal possible relative er-

ror (MPRE), which represents the maximum possible

relative deviation of the estimated O D matrix from

the true one. Based on this concept (Yang and Zhou,

1998) proposed several location rules. In this paper,

since the scanner location problem is of different na-

ture to the counting location problem based on link

ﬂows, we derive an analogous formulation based on

prior link and ﬂow values and the following measure

(RMSRE, root mean squared relative error):

RMSRE =

∑

i∈I



− t



, (1)

where t

and t

are the prior and estimated ﬂow of

O D -pair i, respectively, and m is the number of O D -

pairs belonging to the set I . Note that we propose this

alternative formulation because our model uses prior

information and we also assume that the real network

ﬂows will be similar to those given by the prior ap-

proach, therefore our models try to reproduce through

an estimation method the prior O D pair ﬂows as ex-

actly as possible, when other information is not avail-

able. Since the prior O D pair ﬂowst

are known, they

are used to calculate the relative error.

Given the set R of all possible routes, if R

is the

set of routes belonging to O D -pair i, we have t

∑

r∈R

, and then the RMSRE can be expressed as:

RMSRE =

∑

i∈I

−

∑

r∈R

, (2)

where y

is a binary variable equal to one if route r is

identiﬁed uniquely (observed) by the scanned links,

and zero otherwise. Note that the minimum possible

RMSRE-value corresponds to y

= 1; ∀r ∈ R, where

= t

and RMSRE=0. However, if n

∑

r∈R

≤ n

then RMSRE> 0, and then, one interesting question

is: how do we select the routes to be observed so that

the RMSRE is minimized? From (2) we obtain

m× RMSRE

∑

i∈I

1−

∑

r∈R

, (3)

where it can be concluded that the bigger the value

∑

r∈R

the lower the RMSRE. If the set of

routes is partitioned into observed (O R ) and unob-

served (U R ) routes associated with y

= 1 or y

= 0,

respectively, (3) can be reformulated as follows

m× RMSRE

∑

i∈I



1−

∑

r∈(R

∩O R )



∑

i∈I



∑

i∈(R

∩U R )



(4)

so that routes to be observed (y

= 1) should be chosen

minimizing (4).

The main shortcoming of equations (3) or (4) is

their quadratic character which makes the RMSRE

minimization problem to be nonlinear. Alternatively,

the following RMARE (root mean absolute value rel-

ative error) based on the mean absolute relative error

PREDICTING TRAFFIC FLOWIN ROAD NETWORKS - Using Bayesian Networks with Data from an Optimal Plate

Scanning Device Location

553

norm can be deﬁned:

RMARE =

∑

i∈I



− t



∑

i∈I



−

∑

r∈R



(5)

and since the numerator is always positive for error

free scanners (0 ≤

∑

r∈R

≤ t

; ∀i ∈ I), the abso-

lute value can be dropped, so that the RMARE as a

function of the observed and unobserved routes is

RMARE = 1 −

∑

i∈I

∑

r∈(R

∩O R )

∑

i∈I

∑

r∈(R

∩U R )

(6)

which implies that minimizing the RMARE is equiv-

alent to minimizing the sum of relative route ﬂows of

unobserved routes, or equivalently, maximize the sum

of relative route ﬂows of observed routes.

Note also that even though the knowledge of prior

O D pair ﬂows could be difﬁcult in practical cases,

the aim of the proposed formulation is determining

which O D ﬂows are more important than others in

order to prioritize their real knowledge. In fact the

prior O D matrix is only used as a weighting factor

for O-D pairs ﬂows. Alternatively, the MPRE crite-

rion proposed by (Yang et al., 1991) could be used for

those cases where a prior O-D matrix is unavailable.

Note that existing methods such us the one proposed

by (Yang and Zhou, 1998) and according to their max-

imal ﬂow-interception rule, also use a ﬂow pattern as-

sociated with a prior O-D matrix.

The ﬁrst location model to be proposed in this pa-

per considers full route observability, i.e. RMSRE=

0, but including budget considerations. In the trans-

port literature, each link, denoted by a, is considered

independently of the number of lanes it has. Obvi-

ously, when trying to scan plate numbers links with

higher number of lanes are more expensive (usually

the number of scanning devices is bigger):

= Minimize

∑

a∈A

(7)

subject to

∑

a∈{A }

(λ

+ λ

)(1− λ

≥ 1

(

∀(r,r

)|r < r

∑

a∈A

> 0

(8)

∑

a∈A

≥ 1;∀r, (9)

where z

is a binary variable taking value 1 if the link

a is scanned, and 0, otherwise, r and r

are paths, Λ is

the route incidence matrix with elements λ

Note that constraint (8) guarantees that the se-

lected subset of scanned links is able to distinguish

the users of any given pair of paths r and r

based on

their scanned plate numbers, i.e. there exists at least

one scanned link which is in path r and not in path

or vice-versa. In addition, constraint (9) ensures

that any route or path contains at least one scanned

link, and therefore information, not only of all O D

pairs but all the routes, becomes available. P

is the

cost of plate scanning link a. Note that constraint

(8) forces to select the scanned links so that every

route is uniquely deﬁned by a given set of scanned

links (every row in the incidence matrix Λ is differ-

ent from the others) and (9) ensures that at least one

link for every route is scanned (every row in the inci-

dence matrix Λ contains at least one element different

from zero). Both constraints (8) and (9) force to ob-

serve the maximum relative route ﬂow and provide

the full identiﬁability of observed path ﬂows. Note

also that all O D pairs are totally covered. In addi-

tion, this model allows us the estimation of the re-

quired budget resources B

∗

∑

a∈A

∗

for covering

all O D pairs in the network which obviously must be

the minimum for full identiﬁability of routes. How-

ever, budget is limited in practice, meaning that some

O D pairs or even some routes may remain uncovered,

consequently based on (6) the following model is pro-

posed in order to observe the maximum relative route

ﬂow:

= Maximize

y,z

∑

∀i∈I

∑

r∈R

(10)

subject to

∑

a∈{A }

(λ

+ λ

)(1− λ

≥ y

(

∀(r,r

)|r < r

∑

a∈A

> 0

(11)

∑

a∈A

≥ y

; ∀r, (12)

∑

a∈A

≤ B , (13)

where f

and t

are the route and O D -pair ﬂows, re-

spectively, of a prior O D matrix, y

is a binary vari-

able equal to 1 if route r can be distinguished from

others and 0 otherwise, z

is a binary variable which

is 1 if link a is scanned and 0 otherwise, and B is the

available budget.

Constraint (11) guarantees that the route r is able

to be distinguished from the others if the binary vari-

able y

is equal to 1. Constraint (12) ensures that

the route which is able to be distinguished contains at

least one scanned link. Both constraints (11) and (12)

ensure that all routes such that y

= 1 can be uniquely

identiﬁed using the scanned links. It is worthwhile

mentioning that using y

instead of 1 in the right hand

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

554

side of constraints (11) and (12) immediately con-

verts into inactive the constraint (9) for those routes

the ﬂow of which are not fully identiﬁed.

Note that the full identiﬁability of observed path

ﬂows is included in the optimization itself and it will

be ensured or not depending on the available budget

B , i.e. depending on whether or not constraint (13)

becomes active. For example, if the available bud-

get equals the optimal value of the objective function

given by model M

(B = B

∗

), model M

provides full

O D coverage. Note also that previous models can

be easily modiﬁed in order to include some practical

considerations as for example the fact that some de-

tectors are already installed and additional budget is

available. To do that one only need to include the fol-

lowing constraint to models M

or M

= 1; ∀a ∈ O L . (14)

where O L is the set of already observed links (links

with scanning devices already installed).

3 THE PROPOSED MODEL FOR

TRAFFIC PREDICTION

Bayesian network models have been used frequently

to solve a wide range of practical problems (see, for

example, (Castillo et al., 1995), (Bouckaert et al.,

1996), (Castillo et al., 1996), (Castillo et al., 1999),

or (Castillo and Kjaerulff, 2003)). In this section we

have used the Bayesian network tool to built a model

for trafﬁc prediction using data from plate scanning

devices. In addition a detailed description and justiﬁ-

cation of its main assumptions are presented.

3.1 Bayesian Networks

A Bayesian network is a pair (G ,P ), where G

is a directed acyclic graph of a set of nodes X,

which are the random variables, and a set P =

{p(x

|π

),..., p(x

|π

)} of n conditional probability

densities, where Π

is the set of parents of node X

in G . The graph G contains qualitative information

about the relationships among the variables, and P

contains the quantitative information and deﬁnes the

associated joint probability density of all nodes as

p(x) =

∏

i=1

p(x

|π

). (15)

Bayesian networks are very useful to represent

the statistical relationship among multivariate random

variables. In particular, (Sun et al., 2006), (Castillo

et al., 2008b; Castillo et al., 2008c) apply Bayesian

networks to trafﬁc ﬂow problems.

Bayesian networks have a high practical interest

because: (a) the conditional independence relations

among the X variables can be inferred directly from

the graph G , which is relevantto given variables when

the knowledge of other variables become available,

and (b) the updating of probabilitiescan be very easily

done when new variables become known.

In this paper we use Gaussian Bayesian networks

(GBN), that is, Bayesian networks such that their joint

probability distributions of all their variables are mul-

tivariate normal N(µ,Σ) distributions. This assump-

tion is very common in the transport literature

3.2 Updating Information in GBN after

having Evidences

When one works with Gaussian Bayesian networks, it

is possible to introduce the observed value of several

variables of the network an computing the probability

distribution of the rest of variables.

Let Y and Z be two sets of random variables rep-

resenting unobserved and observed variables, respec-

tively, and having a multivariate Gaussian distribution

with mean vector and covariance matrix given by

µ =





and Σ =





respectively, where µ

and Σ

are the mean vector

and covariance matrix of Y, µ

and Σ

are the mean

vector and covariance matrix of Z, and Σ

is the co-

variance ofY and Z. Then the conditional probability

distribution (CPD) of Y given Z = z (the evidence)

is multivariate Gaussian with mean vector µ

Y|Z=z

and

covariance matrix Σ

Y|Z=z

that are given by

Y|Z=z

= µ

+ Σ

−1

(z− µ

), (16)

Y|Z=z

= Σ

− Σ

−1

. (17)

Note that the conditional mean µ

Y|Z=z

depends on

z but the conditional variance Σ

Y|Z=z

does not. There-

fore equations (16) and (17) suggest a procedure to

calculate the means and variances of any subset of

variablesY ⊂ X, given a set of evidential nodes Z ⊂ X

whose values are Z = z.

3.3 Model Assumptions

Assuming the route ﬂows are multivariate random

variables, we build a Gaussian Bayesian network us-

ing the special characteristics of trafﬁc ﬂow variables.

To this end, we consider the route ﬂows as parents

and the subsets of scanned link ﬂows as children

and reproduce the conservation law constraints in an

exact or statistical (i.e., with random errors) form. In

PREDICTING TRAFFIC FLOWIN ROAD NETWORKS - Using Bayesian Networks with Data from an Optimal Plate

Scanning Device Location

555

our Gaussian Bayesian network model we make the

following assumptions:

Assumption 1. It is clear that the F of route ﬂows

random variables are correlated. For example, dur-

ing peak commuting periods trafﬁc increases for all

routes and strong weather conditions reduce trafﬁc

ﬂows in all routes. In order to represent these corre-

lations and obtain the associated variance-covariance

matrix, we make the following assumption:

= k

U + η

, (18)

where k

,r = 1, ... ,m are positive real constants, U

is a normal random variable N(µ

,σ

), and η

are

independent normal N(0,γ

) random variables. The

meanings of these variables are as follows:

U: Random positive variable that measures the level

of total mean ﬂow. This means that ﬂow varies

randomly and deterministically in situations simi-

lar to those being analyzed (weekend period, labor

day, beginning or end of a holiday period, etc.).

K: Column matrix whose element k

measures the

relative weight of the route r ﬂow with respect to

the total trafﬁc ﬂow (including all routes). It mea-

sures the importance or level of trafﬁc ﬂow asso-

ciated with route r (the larger the value of k

, the

larger the ﬂow trafﬁc in route r).

η : Vector of independent random variables with null

mean such that its r element measures the vari-

ability of the route r ﬂow with respect to its mean.

Then, we have

F =



K | I







−−





(19)

and the variance-covariance matrix Σ

of F is



K | I



(U,η)





−−





(20)

= σ

+ D

, (21)

where the matrices Σ

(U,η)

and D

are diagonal.

Assumption 2. The ﬂows associated with the combi-

nations of scanned link ﬂows and counted link ﬂows

can be written as

W = ∆F+ ε, (22)

where the W

variables represent the trafﬁc ﬂow as-

sociated with each feasible combination of scanned

links, which is related to the route ﬂows; δ

(element

of matrix ∆) is 1 if route r contains all and only the

links associated with W

, and ε = (ε

,ε

,. ..,ε

) are

mutually independent normal random variables, inde-

pendent of the random variables in F, and ε

has mean

E(ε

) and variance ψ

;s = 1, 2, ... ,n. The ε

repre-

sents the error in the corresponding subset of scanned

links. In particular, they can be assumed to be null i.e.

the plate data is assumed error free.

Then, we have









I | 0

− + −

∆ | I









−−





which implies that the mean E[(F,W)] is

E[(F,W)] =





E(U)K

− − − − − − −

E(U)∆K+ E(ε)





, (23)

and the variance-covariance matrix of (F,W) is

(F,W)





| Σ

∆

−− + − − −−

∆Σ

| ∆Σ

∆

+ D





. (24)

All these assumptions imply that the joint PDF of

,. ..,F

,. ..,W

) can be written as

f( f

, f

,.. ., f

,.. ., w

) =

N(µ

,Σ

)

( f

, f

,.. ., f

)

∏

s=1

N(µ

∑

r∈Π

∆

( f

−µ

),ψ

)

(25)

To complete our Bayesian network model we need to

deﬁne the graph. Any probability distribution can be

represented by a directed graph. The only problem,

to build the Bayesian network graph, is the number of

links required, that can be large if the order of nodes

is not adequately chosen.

In this paper we give what we think is the most

convenient graph (see Fig. 2): the route ﬂows F

are

the parents of all link ﬂow combinations W

used by

the corresponding travelers, and the error variables

are the parents of the corresponding ﬂows, that is, the

are the parents of theW

, and the η

are the parents

of the F

. Finally, the U variable is on top (parent)

of all route ﬂows, because it gives the level of them

(high, intermediate or low). This solves the problem

of “parent” being not well deﬁned, without the need

for recursion - in general graphs, one could seemingly

have a “deadlock” situation in which it is not clear

what node is the parent of which other nodes.

In this paper we consider the simplest version of

the proposed model, which considers only the route

ﬂows, and the scanned link ﬂow combinations. There-

fore, a further requires that a model with all variables

must be built i.e. including the mean and variance

matrix of the all variables (U, η

;r = 1,2,.. .,m and

;s = 1,2,.. . ,n).

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

556

3.4 Trafﬁc Prediction

Once we have built the model, we can use its JPD

(25) to predict route and link trafﬁc ﬂows when some

information becomes available. The idea consists of

using the joint distribution of routes ﬂows conditioned

on the available information. In fact, since the re-

maining variables (those not known) are random, the

most informative item we can get is its conditional

joint distribution, and this is what the Bayesian net-

work methodology supplies. In this section we pro-

pose an step by step method to implement the plate

scanning-Bayesian network model:

Step 0: Initialization Step. Assume an initial K

matrix (for example, obtained from solving a SUE

problem for a given out-of-date prior OD-pair

ﬂow data), the values of E[U] and σ

, and the

matrices D

and D

Step 1: Select the Set of Links to be Scanned.

The set of links to be scanned must be selected.

This paper deals with this problem in Section 2

providing several methods to select the best set of

links to be scanned.

Step 2: Observe the Plate Scanning Data. The

plate scanning data w

are extracted.

Step 3: Estimate the Route Flows. The route ma-

trix F with elements f

are estimated using the

Bayesian network method, i.e., using the formu-

las (see (16) and (17)):

E[F] = E[U]K (26)

E[W] = E[U]∆K+ E[ε] (27)

= Diag(νE[F]) , (28)

= σ

+ D

(29)

= Σ

∆

(30)

= Σ

(31)

= ∆Σ

∆

+ D

(32)

E[F|W = w] = E[F] + Σ

−1

(w− E[W])

(33)

F|W=w

= Σ

− Σ

−1

(34)

E[W|W = w] = w (35)

W|W=w

= 0 (36)

F = E[F|W = w]|

(F,W)=F

(37)

where ν is the coefﬁcient of variation selected for

the η variables, and we note that F and W are

the unobserved and observed components, respec-

tively.

Step 4. Obtain the F Vector. Return the the f

route ﬂows as the result of the model. Note that

from F vector, the rest of trafﬁc ﬂows (link ﬂows

and OD pair ﬂows) can be easily obtained.

4 EXAMPLE OF APPLICATIONS

In this section we illustrate the proposed methods by

their application to a simple example. We assume that

plate scanning trafﬁc data have no errors.

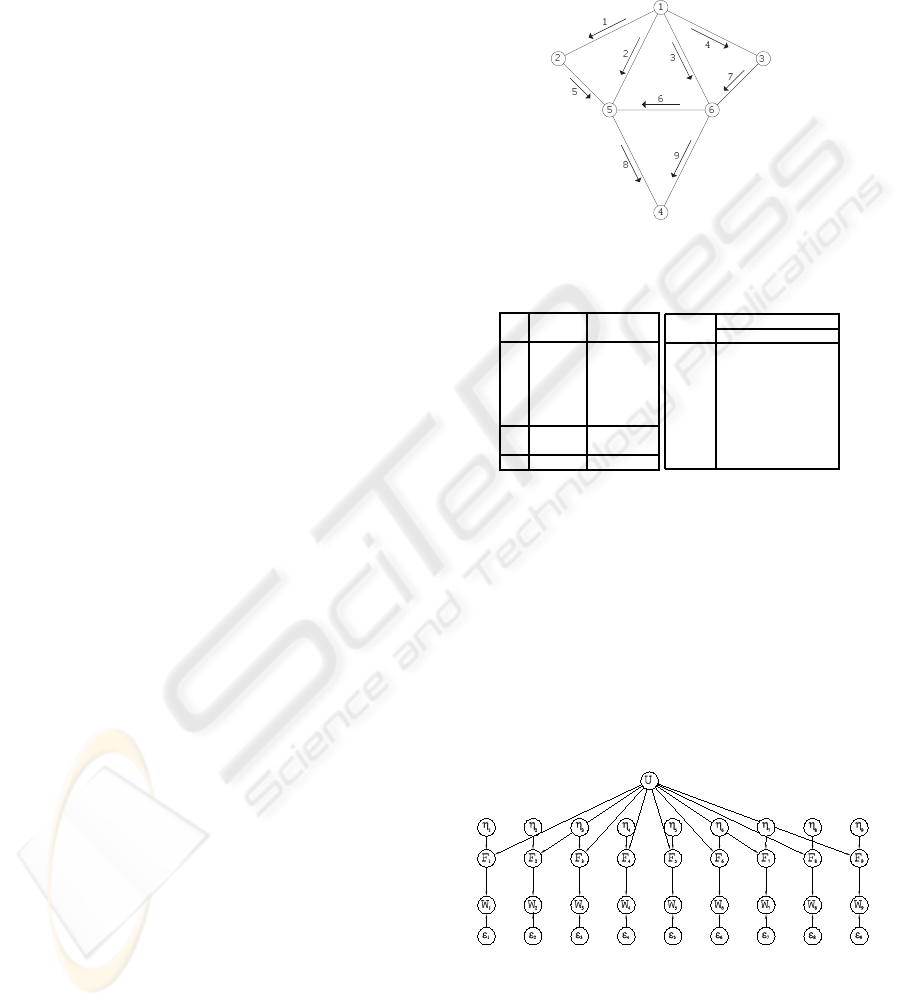
Figure 1: The elementary example network.

Table 1: Required data for the simple example.

path code

OD (r) Links

1-4 1 1 5 8

1-4 2 2 8

1-4 3 3 9

1-4 4 3 6 8

1-4 5 4 7 9

1-4 6 4 7 6 8

2-4 7 5 8

2-4 8 7 6 8

3-4 9 7 9

set code Scanned links

(s) 1 2 3 4 7 8

1 X X

2 X X

3 X

4 X X

5 X X

6 X X X

7 X

8 X X

9 X

Consider the network in Fig. 1 with the routes and

OD-pairs in Table 1, which shows the feasible combi-

nation of scanned links after solving the M

model.

As described in Section 3, the graph of the as-

sociated Bayesian network is shown in Fig. 2 for

S L = {1,2,3,4,7,8}. Note that the route node F

has

as parents only node U and η

, and any ﬂow from

plate scanning data node W

has its associated routes

as parents, i.e., those routes with all and only all the

corresponding subset of scanned links (see Table 1).

Next, the proposed method in Section 3 is applied.

Figure 2: BN associated with the example.

Step 0: Initialization Step. To have a reference

ﬂow, we have considered that the true route ﬂows

are those shown in the second column of Table 2.

The assumed mean value was E[U] = 10 and the

value of σ

is 8. The initial matrix K is obtained

PREDICTING TRAFFIC FLOWIN ROAD NETWORKS - Using Bayesian Networks with Data from an Optimal Plate

Scanning Device Location

557

by multiplying each true route ﬂow by an inde-

pendent random uniform U(0.4, 1.3)/10 number.

The D

is assumed diagonal matrix, the diagonal

of which are almost null (0.000001) because we

have assumed error free in the plate scanning pro-

cess. D

is also a diagonal matrix which values

are associated with a variation coefﬁcient of 0.4.

Step 1: Select the Set of Links to be Scanned.

The set of links to be scanned have been selected

using the M

model for different available budget,

i.e. using the necessary budget for the devices

needed to be installed in the following links:

S L ≡ {1,2,3,4,7,8}; S L ≡ {1,4,5,7,9};

S L ≡ {1,4,7,9}; S L ≡ {4,7,9};

S L ≡ {1,5}; S L ≡ {2}.

Step 2: Observe the Plate Scanning Data. The

plate scanning dataW

is obtained by scanning the

selected links (a detailed explanation of how this

can be done appears in (Castillo et al., 2008a)).

Step 3: Estimate the Route Flows. The route

ﬂows F with elements f

are estimated using the

Bayesian network method and the plate scanning

data, i.e., using the formulas (26)-(37)

Table 2: Route ﬂow estimates using BN and LS approaches.

True Scanned links

Route ﬂow Method 0 1 2 3 4 5 6

1 5.00 BN 4.26 4.35 5.00 4.91 5.00 5.00 5.00

LS 4.26 4.26 5.00 4.26 5.00 5.00 5.00

2 7.00 BN 6.84 7.00 7.76 7.89 7.91 7.85 7.00

LS 6.84 7.00 6.84 6.84 6.84 6.84 7.00

3 3.00 BN 3.45 3.52 3.91 3.00 3.00 3.00 3.00

LS 3.45 3.45 3.45 3.00 3.00 3.00 3.00

4 5.00 BN 3.00 3.07 3.41 3.46 3.47 3.45 5.00

LS 3.00 3.00 3.00 3.00 3.00 3.00 5.00

5 6.00 BN 5.36 5.47 6.08 6.00 6.00 6.00 6.00

LS 5.36 5.36 5.36 6.00 6.00 6.00 6.00

6 4.00 BN 3.37 3.45 3.82 4.00 4.00 4.00 4.00

LS 3.38 3.38 3.38 4.00 4.00 4.00 4.00

7 10.00 BN 8.90 9.08 10.00 10.25 10.28 10.00 10.00

LS 8.90 8.90 10.00 8.90 8.90 10.00 10.00

8 7.00 BN 3.97 4.06 4.50 7.00 7.00 7.00 7.00

LS 3.97 3.97 3.97 7.00 7.00 7.00 7.00

9 5.00 BN 5.45 5.57 6.18 5.00 5.00 5.00 5.00

LS 5.45 5.45 5.45 5.00 5.00 5.00 5.00

The method has been repeated for different sub-

sets of scanned links shown in step 2 of the process.

The resulting predicted route ﬂows are shown in Table

2. The ﬁrst rows correspond to the route predictions

using the proposed model. With the aim of illustrat-

ing the improvement resulting from the plate scanning

technique using Bayesian networks when compared

with the standard method of Least Squares (LS), for

example (see (Castillo et al., 2008a)), we have imple-

mented this model using the same data. The results

appear in the second rows in Table 2. A compari-

son of the results obtained from both methods con-

ﬁrm that the plate scanning method using Bayesian

networks outperforms the standard method of Least

Squares for several reasons:

• The BN tool provides the random dependence

among all variables. This fact allows us improve

the route ﬂow predictions even though when we

have no scanned link belonged to this particular

route. Note that using the LS approach the predic-

tion is the prior ﬂow (the fourth column in Table

2, i.e with 0 scanned links in the network)

• The BN tool provides not only the variable pre-

diction but also the probability intervals for these

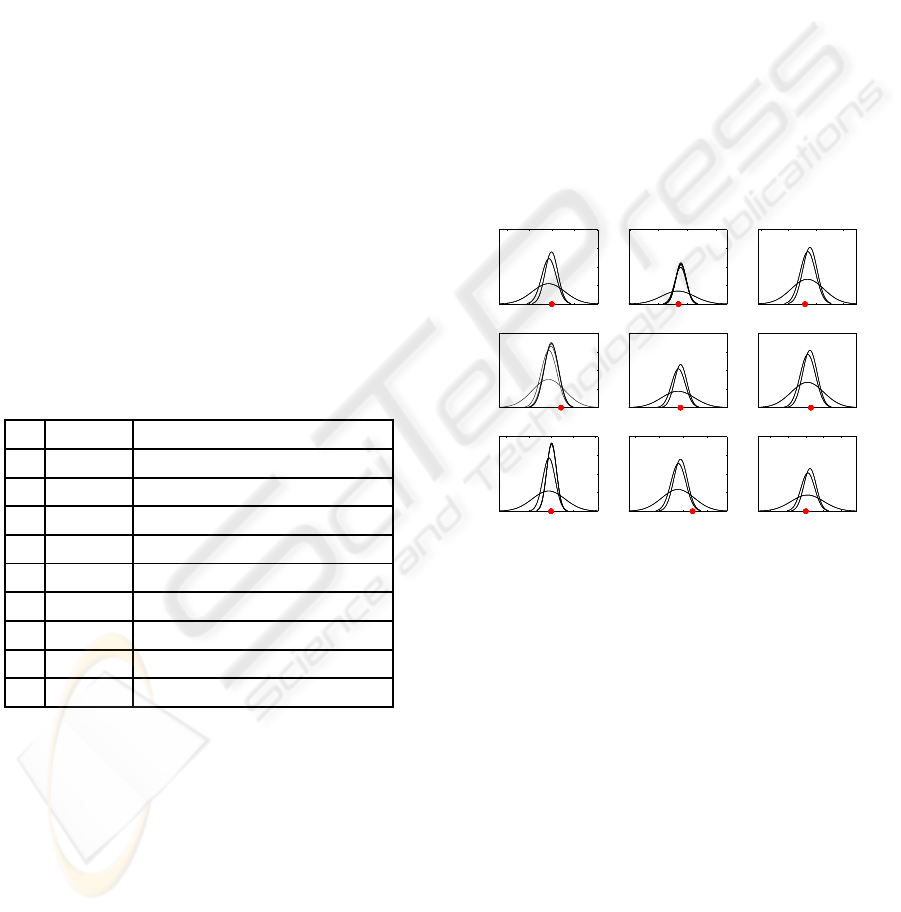
predictions using the JPD function. Fig. 3 shows

the conditional distributions of the route ﬂows the

different items of accumulated evidence. From

left to right and from top to bottom F

.. . pre-

dictions are shown. In each subgraph the dot rep-

resents the real route ﬂow in order to analyze the

predictions.

−5 0 5 10 15

0.1

0.2

0.3

0.4

−10 0 10 20

0.1

0.2

0.3

0.4

−5 0 5 10

0.1

0.2

0.3

0.4

0 5 10

0.1

0.2

0.3

0.4

−5 0 5 10 15

0.1

0.2

0.3

0.4

−5 0 5 10

0.1

0.2

0.3

0.4

−10 0 10 20 30

0.05

0.1

0.15

0.2

−5 0 5 10

0.1

0.2

0.3

0.4

−5 0 5 10 15

0.1

0.2

0.3

0.4

Figure 3: Conditional distribution of the route ﬂows.

It is necessary to point out that the proposed mod-

els have been applied to real size networks as for ex-

ample the city of Cuenca (Spain) but the results can-

not be showed for space problems. The network con-

sists of 672 links, 232 nodes, 139 OD-pairs and 528

routes. In this network, 100 scanned links are sufﬁ-

cient for full observability using M

proposed model.

5 CONCLUSIONS

The main conclusions that can be drawn from this pa-

per are the following:

1. Bayesian networks are very natural tools for re-

producing the random dependence structure of

trafﬁc ﬂows including not only OD-pair and link

ﬂows but route ﬂows and ﬂows associated with

subsets of links. Therefore, the combination of

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

558

Bayesian networks and scanned link ﬂows seems

to be a very good and practical tool to predict traf-

ﬁc ﬂows. The example in this paper illustrate the

improvement of this combination when combined

with other methods and shows that it outperforms

other alternatives.

2. The updating techniques for Bayesian networks

allow us obtaining the distribution of route ﬂows

conditioned by the observed ﬂows, accounting for

all the information available (evidences).

3. The knowledge of plate scanned observations

modify substantially the means and reduces the

variance of the route ﬂows leading to more precise

predictions, which improve with increasing num-

ber of scanned links and can be exact for an ade-

quate selection of the set of scanned and counted

links i.e. using the M

proposed model.

4. Several models have been presented for an ade-

quate selection and location of plate scanning de-

vices including budget constraints together with

the consideration of already existing devices. In

addition, they allow us improving the route ﬂow

estimations.

5. Errors in scanned links can produce important al-

terations of the parameters estimates, because sev-

eral users of several routes can be confounded if

they are not been observed in some links. This

aspect is not the focus of this paper and its full

treatment will be dealt with in an outgoing work.

In any case one approach for solving this problem

is treated in (Castillo et al., 2008a).

REFERENCES

Bouckaert, R., Castillo, E., and Guti´errez, J. M. (1996). A

modiﬁed simulation scheme for inference in Bayesian

networks. International Journal of Approximate Rea-

soning, 14(1):55–80.

Cascetta, E. and Nguyen, S. (1988). A uniﬁed frame-

work for estimating or updating origin/destination ma-

trices from trafﬁc counts. Transportation Research,

22B:437–455.

Castillo, E., Guti´errez, J. M., and Hadi, A. S. (1995). Para-

metric structure of probabilities in bayesian networks.

In European Conference on Symbolic and Quantita-

tive Approaches to Reasoning and Uncertainty (EC-

SQARU 95), pages 89–98. Symbolic and Quantitative

Approaches to Reasoning and Uncertainty.

Castillo, E., Guti´errez, J. M., and Hadi, A. S. (1996). A new

method for efﬁcient symbolic propagation in discrete

bayesian networks. Networks, 28(1):31–43.

Castillo, E. and Kjaerulff, U. (2003). Sensivity analy-

sis in Gaussian Bayesian networks using a symbolic-

numerical technique. Reliability Engineering and Sys-

tem Safety, 79/2:139–148.

Castillo, E., Men´endez, J. M., and Jim´enez.P (2008a). Trip

matrix and path ﬂow reconstruction and estimation

based on plate scanning and link observations. Trans-

portation Research B, 42:455–481.

Castillo, E., Men´endez, J. M., and S´anchez-Cambronero, S.

(2008b). Predicting trafﬁc ﬂow using Bayesian net-

works. Transportation Research B, 42:482–509.

Castillo, E., Men´endez, J. M., and S´anchez-Cambronero, S.

(2008c). Trafﬁc estimation and optimal counting lo-

cation without path enumeration using Bayesian net-

works. Computer Aided Civil and Infraestructure En-

gineering, 23:189–207.

Castillo, E., Sarabia, J. M., Solares, C., and G´omez,

P. (1999). Uncertainty analyses in fault trees and

Bayesian networks using form/sorm methods. Reli-

ability Engineering and System Safety, 65:29–40.

Conejo, A., Castillo, E., M´ınguez, R., and Garc´ıa-Bertrand,

R. (2006). Decomposition Techniques in Mathemati-

cal Programming. Engineering and Science Applica-

tions. Springer, Berlin.

Doblas, J. and Benitez, F. G. (2005). An approach to esti-

mating and updating origin-destination matrices based

upon trafﬁc counts preserving the prior structure of

a survey matrix. Transportation Research, 39B:565–

591.

Praskher, J. N. and Bekhor, S. (2004). Route choice mod-

els used in the stochastic user equilibrium problem: a

review. Transportation Reviews, 24:437–463.

Sun, S. L., Zhang, C. S., and Yu, G. Q. (2006). A Bayesian

network approach to trafﬁc ﬂow forecasting. IEEE

Transactions on Intelligent Transportation Systems,

7(1):124–132.

Tebaldi, C. and West, M. (1996). Bayesian inference on

network trafﬁc using link count data. Journal of the

American Statistical Association, 93:557–576.

Van Zuylen, H. J. and Willumsen, L. (1980). Network to-

mography: The most likely trip matrix estimated from

trafﬁc-counts. Transportation Research B, 14:291–

293.

Watling, D. (1994). Maximum likelihood estimation of

an origindestination matrix from a partial registration

plate survey. Transportation Research, 28B:289–314.

Yang, H., Iidia, Y., and Sasaki, T. (1991). An analysis of

the realiability of an origin-destination trip matrix es-

timated from trafﬁc counts. Transportation Research,

25B:351–363.

Yang, H. and Zhou, J. (1998). Optimal trafﬁc counting loca-

tions for origin-destination matrix extimation. Trans-

portation Research, 32B:109–126.

PREDICTING TRAFFIC FLOWIN ROAD NETWORKS - Using Bayesian Networks with Data from an Optimal Plate

Scanning Device Location

559