
IMPROVING AIRCRAFT MAINTENANCE WITH INNOVATIVE
PROGNOSTICS AND HEALTH MANAGEMENT TECHNIQUES
Case of Study: Brake Wear Degradation
Susana Ferreiro and Aitor Arnaiz
Fundacion TEKNIKER, Eibar, Gipuzkoa, Spain
Keywords: Aircraft maintenance, Aircraft availability, Prognosis, Probabilistic model, Reliability analysis.
Abstract: Maintenance is going through to major changes in a lot of activity fields where the current maintenance
strategy must adjust to the new requirements. The aeronautics industry belongs to one these activity fields
which are trying to carry out important changes around its maintenance strategy. It needs to minimize the
cost for the maintenance support and to increase its operational reliability and availability (avoiding delays,
cancellations, etc) which would lead to a further decrease in costs. However, to support this change, it
requires transforming the traditional corrective maintenance practice of “fail and fix” to “prevent and
predict”. The aim of this article is to show the usefulness and the benefits of innovative techniques such as
Bayesian Networks to support an intelligent function “decision support”, the basis for the new type of
maintenance strategy based on prediction and prognosis. It helps to achieve a maximum optimization of
resources and operational availability while minimizing economic costs, and replaces the current
maintenance carried out in the aircraft industry up to now.
1 INTRODUCTION
Today’s maintenance is going through major
changes practically in all of its activity fields. In
aeronautics industry, the need involves minimize the
maintenance support and increase efficiency of the
process. All airlines are striving for reduce the cost
of aircraft maintenance while ensuring aircraft
reliability and availability (eliminating delays and
cancellations) with new technologies initiatives. But
although there are more and more novel
maintenance solutions, it is still unscheduled process
and it remains a significant problem.
For example, the current decision support in
aircraft maintenance is limited to a GO or NO-GO
decision for the aircraft next flight based on a pre
flight check of certain components of the aircraft.
This check is part of the ‘Maintenance Execution’
which takes care of on-aircraft and off-aircraft
maintenance, and includes all checks executed in the
hangar. Usually, the pre flight check is based on an
assessment of the Maintenance Minimum
Equipment List (MMEL) for relevant items. It
means that the decision support is a reactive process,
focused on unscheduled (trouble shooting) or
deferred maintenance activities, which involves a
Figure 1: Not detected failures at early stage could be
cause a delay or cancellations in the next flight, impacting
directly into the operational planning of the aircraft/fleet.
high percentage of direct operating cost in aircraft
maintenance (Fig.1).
Prognostic Health Management (PHM) systems
are working to overcome this problem by integrating
all the condition monitoring, health assessment and
prognostics into an open modular architecture and
then further supporting the operator by adding
intelligent decision support tools.
The new decision support presented in this paper
includes the “operational support” unit (Fig. 2) and
adds a proactive function to the actual maintenance
procedure, where GO and NO-GO decision will be
supported by aircraft health assessment.
568
Ferreiro S. and Arnaiz A. (2010).
IMPROVING AIRCRAFT MAINTENANCE WITH INNOVATIVE PROGNOSTICS AND HEALTH MANAGEMENT TECHNIQUES - Case of Study: Brake
Wear Degradation.
In Proceedings of the 2nd International Conference on Agents and Artificial Intelligence - Artificial Intelligence, pages 568-575
DOI: 10.5220/0002718405680575
Copyright
c
SciTePress

On top of “operational support”, the “operational
risk assessment” concept appears: an extended
function of the operational support for calculating
and evaluating the operational risk for aircraft and
fleet operation. It creates or reshapes the long-term
maintenance plan based on aircraft conditional view,
as well as it evaluates the impact of virtual
maintenance plan on alternative future operational
scenarios and provides quantified operational risk
indicators for further decision support.
Figure 2: Operational support.
Conditional View module is the first module of
“operational support” and it will provide remaining
useful life (RUL) estimated (with their associated
confidence level) in real operation time. Conditional
View provides a basis for operational risk
estimation, along with other sources of information
such as operational constraints, economic/safety
information, etc.
2 CONDITIONAL VIEW MODEL
ISSUES
Conditional View generates an operational view of
the aircraft taking into account component health
status and remaining useful life and updating this
data with specific information concerning future
usage of the aircraft that can be derived from
operational plan.
In order to develop the Conditional View model,
several issues must be taken into account. First, as
expressed in (Byington, 2002), there are basically
three types of information that may be the basis of
the RUL prediction in prognostic approaches:
Statistical models: knowledge based just on
failure probabilities coupling with expert
judgments (reliability data).
Physical or mathematical models:
knowledge based on parameters and
connections between them to study
complex system behaviour. This type of
model is validated physically at test-
benches.
Models based on condition or performance
monitoring: normally knowledge based on
the identification of partial information
(condition data) with the model that allows
deriving incomplete models of the
degradation of monitored systems.
Given this, it is a key point to achieve an
appropriate confidence levels. This task involves
two main sources of uncertainties that should be
quantified to improve and adapt RUL predictions:
Original RUL estimations (at current time)
are normally set up as part of laboratory
work including mathematical, physical
and/or statistical modelling together with an
expert criterion. As a result of uncertainties
included in the model (data incompleteness,
model incompleteness…) there is an
uncertainty addition to every RUL
prediction (Díez, 2000).
RUL predictions (at future time) based on
the prediction of the RUL assuming input
parameters on the model took from
expected usage.
Figure 3: Confidence loss.
These two sources of uncertainty are translated
into confidence loss and it depends on the window
of the prediction. Figure 3 shows how confidence
bounds increase over the time as well as the
confidence loss.
Adaptation and knowledge update is another
change relates to the need to keep Conditional View
updated. Once there is a knowledge based system
(from experience or historical data), there exist
many motivations for learning and knowledge
changing, as it explains in (Gilabert, 2006).
Conditional View performs an adaptive prognosis
based on fleet feedback. Initially, prognosis will be
based on an initial model to predict the RUL with
the limits of warning, but it will be improved
(adapted) as more knowledge (concerning with
degradation trends, or with relations between aircraft
usage and degradation) is available. Conditional
IMPROVING AIRCRAFT MAINTENANCE WITH INNOVATIVE PROGNOSTICS AND HEALTH MANAGEMENT
TECHNIQUES - Case of Study: Brake Wear Degradation
569

view uses fleet feedback such as fleet statistics and
operational usage to compare aircraft degradation
patterns against initial RUL degradation pattern.
According to the characteristics, Conditional
View should be use technologies that provide
accurate estimation for degradation and reliability
models, abilities to include confidence information
as part of estimation, to link usage-based
information as part of the input information
(influence factors) of the models and to re-assess
and modify models from feedback information.
The next sections show Conditional View
techniques for the aircraft’s brake wear prediction
(#UC1: Brake Wear – based on Bayesian Networks).
The basis of Bayesian Networks will be explained in
previous sections.
3 BAYESIAN NETWORKS
OVERVIEW
Bayesian Network (BN) is a model representation
for reasoning under uncertainty. Formally, its
representation is a directed acyclic graph (DAG)
where each node represents a random variable and
edges represent (often causal) dependence relations
among them. Thus, each variable represents a unique
event or hypothesis, it has a finite set of mutually
exclusive states: X={x
1
, … , x
n
} and there must be a
state for each possible value and their conditional
probabilities.
If the variable is discrete, the conditional
probabilities distribution (CPD) is represented as a
conditional probabilities table (CPT), which gives
the probability that the node takes on each of its
different states for each combination of the states of
its parents. Figure 4 shows an example, in which all
the nodes are discrete and binary (with two possible
values, denoted by T=true and F=false). There are
two events which could cause that C3=T: C1=T or
C2=T. Also, when it C2=T, the C1 usually does not
turned on.
Otherwise, if the variable is continuous, the table
specifies Gaussian (normal) distribution function by
its mean and variance parameters rather than a CPT.
Continuous node has associated a single Gaussian
distribution function for each configuration of its
discrete parents’ states and the mean is linearly
dependent on the states of its continuous parents
(Fig. 5).
Figure 4: Bayesian Network (discrete nodes).
Figure 5: Bayesian Network (discrete & continuous
nodes).
In order to specify Bayesian Network and fully
represent the joint probability distribution to take
advantage of this paradigm for uncertain knowledge
representation, it is necessary to build a model
(structure and parameters of the network) and
specify for each node X the a-priori probability
distribution for X conditional upon X's parents.
Firstly, there are three main ways for building the
structure of a BN:
By hand: the structure is modelled by an
expert in the domain.
Learning Bayesian network structure from
a data base of cases. There are basically
two approaches: algorithms based on
relations of conditional independence and
algorithms based on the definition of a
metric and the search for the structure that
optimize this metric (score+search).
However, there are also hybrid methods
which are a mixture of both
approximations.
Mixture of the previous ways.
Secondly, a-priori probability distribution for each
node can be obtained from:
Expert criterion and experience, where not
data is needed.
From statistical data used to estimate the
probability distribution in each node.
Mixed approach between expert criterion
and statistic.
Advanced information about Bayesian Network
learning can be found in (Dietterich, 1999) and
(Neapolitan, 2004).
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
570

Moreover, Bayesian Network can be used to
answer probabilistic queries. For example, the
network can be used to find out updated knowledge
of the state of a subset of variables when other
variables (the evidence variables) are observed. In
(Fig. 5), the model can answer what is the
probability of C2=T, given C3=T by using
conditional probability formula:
)3(
)2,3(
)3|2(
TCP
TCTCP
TCTCP
=
==
===
(1)
In the same way, the model showed in (Fig. 6) gives
a conditional Gaussian distribution function for each
of the states of C1:
)1.2,431(
)3,2,"1"1|4(
yxN
yCxCStateCCP
++=
====
(2)
This process of computing the posterior
distribution of variables given evidence is called
probabilistic inference and it is useful in different
situations like diagnostic (abductive reasoning) and
prediction (or deductive reasoning). Introduction to
inference and advanced inference for Bayesian
Networks is available in (Dietterich, 1999).
As an example, for the brake wear, the use case
that will be presented in the next section, Figure 6
represents probabilistic inference computed by
HUGIN software (http://www.hugin.com) after
giving evidences (emphasized in red). The model
consists of four nodes that represent aircraft weight,
landing velocity, brake operation during landing and
brake wear degradation. Brake wear degradation
changes depending on the values for the first three
variables (evidences).
Notice that for the evidence: (aircraft
weight=(148825-inf]; landing velocity=(55.5307-
58.36295],
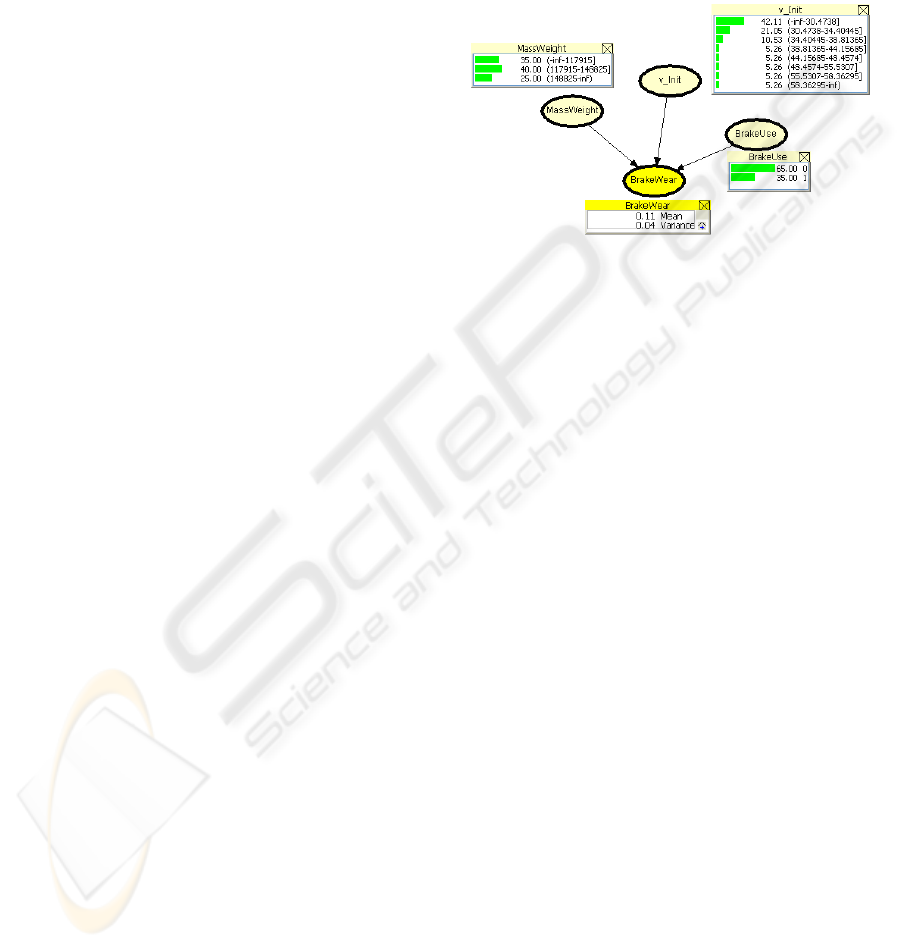
Figure 6: Bayesian Network inference (aircraft weight=
(-inf-117915]; landing velocity=(-inf-30.4738], brake
operation=true).
brake operation=true), the brake wear degradation
value would be higher than for the evidence shown
by the Figure 6 because aircraft weight and landing
velocity have an influence on brake wear
degradation; the higher weight and velocity values,
the higher the degradation.
Eventually, the join probability distribution
(global model) is specified through marginal and
conditional distributions (local models) taking into
account conditional independence relations amongst
the nodes and its parents. This modularity provides
an easy maintenance and reduces the number of
parameters necessary to specify the global model.
This way, the estimation of the parameters is easier,
there is a reduction of the storing needs and the
inference is more efficient.
Furthermore, Bayesian Network is very useful
because it is adaptable. It is possible to build an
initial network with a limited knowledge in a
domain and increase it as new knowledge becomes
available. But the most significant issue is that it is
possible to learn from experience, that is, Bayesian
Networks can refine (conditional) probabilities
specified amongst the states of the nodes by taking
into account real observations. For example,
following with the former example, if we fix the
values for aircraft weight, landing velocity, brake
use operation, and we also fix the real value for
brake degradation for the values we have used, the
net has the capability of propagating and changing
its conditional probabilities, adapting these to the
newly established knowledge.
Bayesian Networks have some advantages over
other techniques (Byington, 2002) (Goode, 1999) as
explained in this section:
They can manage causalities and
uncertainties.
They are an effective technique for solving
diagnostic and prediction problems in
situations where knowledge comes from
different sources because they are able to
mix a priori knowledge and experimental
knowledge.
There are efficient algorithms for
estimating its structure and its a-priori
probability distributions.
It provides with adaptation process in order
to redefine conditional probabilities from
experience (i.e. evidences).
Its representation of knowledge is graphical
and intuitive.
Bayesian Network is being implemented
extensively for different domains. In medicine, it is
used for medical diagnosis such as prostate cancer,
benign prostate hyperplasia, for screening cervical
IMPROVING AIRCRAFT MAINTENANCE WITH INNOVATIVE PROGNOSTICS AND HEALTH MANAGEMENT
TECHNIQUES - Case of Study: Brake Wear Degradation
571
cancer or liver disorders (Onisko, 1998). They are
used for medical prognosis as well, attempting to
predict the future state of the patient with the
evidence we have (symptoms, signs, laboratory test
results, etc) and the treatment (Sierra, 1998). BNs
are also applied in fields as robotic localization and
in the area of mobile robotics (Lazkano, 2007).
Industrial maintenance has evolved from condition
based maintenance to predictive maintenance thanks
to new technologies as BNs, being able to support
the decision process on fault diagnosis and
troubleshooting based on the faults prediction for
non-critical machinery such as elevators and
machine tools (Gilabert, 2006). But there are lots of
references in the literature about the application of
BNs in other fields of application: sensor validation
(Ibargüengoytia, 2006), reliability analysis of
Systems (Doguc, 2009), detection of broken rail for
railway infrastructure (Oukhellou, 2008), diagnosis
of radio access networks of cellular Systems (Barco,
2009), etc.
4 CONDITIONAL VIEW: BRAKE
WEAR DEGRADATION BASED
ON BAYESIAN NETWORKS
Currently, the estimation of brake wear degradation
in aeronautics is performed through a physical
model. It was been developed by British Aerospace
Systems using tests data from Airbus UK and it is
based on the following input parameters:
Aircraft weight
Landing velocity
Brake operation during landing
Flap position
Initial brake temperature
Besides using physical model to make
estimations about brake wear degradation, it may be
possible use Standard Degradation or Simple
Extrapolation as models. Standard Degradation uses
‘standard landing’ wear rate taken as the mean wear
rate based on the experience (0.1mm), whereas
Simple Extrapolation attempts to predict future
brake wear degradation by relying on real data from
historical data. We propose two novel models based
on a Bayesian Network: PhysicalBN & OpBN.
PhysicalBN model takes into account the most
influencing parameters on the degradation
estimation used by the physical model: aircraft
weight (MassWeight), landing velocity (V_Init) and
brake operation during landing (BrakeUse). It was
built from expert criterion to determine the structure
of the net and from a statistical analysis of the data
estimated by the physical model (developed by
British Aerospace Systems) from 3000 samples
randomly generated in order to estimate the
probabilities of each parameter. Figure 7 represents
PhysicalBN and shows the information behind the
main nodes corresponding with the variables
mentioned and their influence on brake wear
degradation.
Figure 7: Bayesian Network (HUGIN researcher 6.8).
PhysicalBN model has some advantages against
the physical model, Standard Degradation or Simple
Extrapolation:
Causalities and probabilities can be
established by an expert criterion and
statistical analysis from test- benches of the
physical model.
The model predicts approximately 0.11mm
wear degradation per flight when there is
no information about future conditions for
aircraft weight, landing velocity and brake
operation during the landing. So, it
simulates well the physical model standard
wear rate.
The model associates brake wear
degradation prediction with a confidence
level of 95%.
However, brake wear degradation may change
substantially depending on flight conditions. A key
issue to highlight is to fit the prognosis modelling to
the available information. This information is not the
same for each case, as can be operational plan
information, historical lifetime measurements, trends
or distributions about the components’ behaviour,
etc.
There is important information into an
operational plan that may be used to predict
degradation parameters. Operational flight plan may
be determine the value of the degradation parameters
and it can be known in advanced. For instance,
aircraft weight typically depends on flight distance,
since the longer the distance the more extra fuel
should be loaded on the aircraft for dealing with odd
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
572

situations, more passengers, more freight, etc. Table
1 shows an operational plan:
Table 1: Operational plan.
FlightNo. Route Flight
distance
(hours)
Check
date
Wear
AF0011 CDG-DEL 12 -
AF0012 DEL-CDG 12 06/01/2008 105.451
… … … …
… … … …
AF348 BOM-
CDG
12 -
AF349 CDG-NRT 19 04/02/2008 62.747
… … … …
Airport
code
Runway
length
Runway
condition
Weather
CDG 3600 Good Wet 90%
DEL 3810 Fair Dry 80%
… … … … …
BOM 3445 Fair Dry 95%
The fact is that for the PhysicalBN is not
possible to have aircraft weight, landing velocity and
brake operation parameters a priori, and their values
are not available before the flight in order to predict
brake wear degradation. But Bayesian Network
structure allows configure causal relations between
operational plan features and PhysicalBN model
inputs affected. Thus, a second Bayesian Network
model (OpBN) is used for explaining the influence
of ‘operational plan parameters’ in the original
model input nodes. The original PhysicalBN is
structurally expanded with the new information
coming from the operational plan and OpBN appears
the following way (Fig. 8):
Now, it is possible to estimate real predictions
concerning the values of the input parameters for the
brake wear estimation at each future flight with
certain assumptions:
FlightDistance represents hours of flight
and it influences into the weight of the
aircraft as it was explained before.
RunwayLength symbolizes runway length
and both landing velocity and brake
operation during the landing will be
dependent on it. Being landing velocity
smaller the shorter the length of the
runway; and being less necessary the use of
brakes as its length increases.
Weather is linked with runway condition. If
the weather is rainy, then the runway surely
will be wet, whereas if it is sunny, the
runway will be dry.
Figure 8: Bayesian Network with operational plan
parameters.
RunwayCondition is the runway condition
and the use of the brake operation during
the landing will be dependent on it. If the
runway is wet, then it is more probable that
brake operation will be off during the
landing. On the other hand, when the
runway is dry, the use of brake operation
during landing will be more probable.
As result, brake wear can be calculated (in mm)
and mapped onto an estimate of RUL (in mm or in
nominal number of landings using ‘standard
landing’ wear rate). But the RUL prediction (RUL
update) error will increase during the computational
process (Fig. 9), having an impact on the operational
risk.
The computational process of RUL prediction starts
as expected usage which is what OpBN can really
forecast (expected usage) linked to RUL estimation,
and it relies on the past behaviour:
Figure 9: Process of computing brake wear RUL.
IMPROVING AIRCRAFT MAINTENANCE WITH INNOVATIVE PROGNOSTICS AND HEALTH MANAGEMENT
TECHNIQUES - Case of Study: Brake Wear Degradation
573

)__
;_()1()(
parametersdataprocess
usageExpectedftRULtRUL −−=
(3)
with
)(_ tusageExpected
normally distributed
being
0
()
R
UL t =initial brake’s thickness (mm)
In order to minimize this confidence loss, two issues
are taken into account:
1. Cumulative Variance and Confidence
Levels.
Assuming brake wear degradation follows a
Gaussian distribution with a 95% of confidence
level for each flight, and further assuming
independence between flights, the loss/gain
assessment of the confidence curve for a whole
distribution is defined as follows by the addition
of these Gaussian distributions:
321
)1(_
meanmeanmean
tusageExpected
=+=
=+
(4)
2
2
2
13
2
)1(
_
σσ
+−=
=+
mean
tlowe
r
Confidence
(5)
2
2
2
13
2
)1(
_
σσ
++=
=+
mean
tuppe
r
Confidence
(6)
where
sd=
σ
2. Status Observation.
After some flights (at time tj) there will be a
check-in at the gate and the brake wear real
degradation will be known. Both confidence
levels and predicted brake wear degradation are
fixed at the same value of real degradation.
Then, it will retrieve 100% of confidence level.
Figure 10 illustrates RUL prediction at time t
0
with confidence levels for the next 11 flights:
PhysicalBN - RUL
27
27.5
28
28.5
29
29.5
30
30.5
ham gva muc mxp her cag tls gib fnc gva muc
Operational Plan (Airports)
RUL (mm)
RealWear (mm)
RUL
Lower
Upper
Figure 10: Results from prediction model.
5 EVALUATION AND FUTURE
ACTIONS
Finally, to evaluate whether it is possible to build
more accurate and adaptable model than the original,
it is shows several results for the case of the brake
wear.
In order to evaluate the goodness of the
PhysicalBN model, the error rate is calculated from
a new dataset of 100 samples by means of MSE
(mean squared error):
00587.0))(
ˆ
(
1
))(
ˆ
,(
1
2
=−=
∑
=
n
i
ii
yxf
n
xfyL
(7)
The error of the model is not significant,
however, it is necessary to evaluate the error for the
computational process of RUL prediction showed in
the Section 4 and compare it with the error of other
algorithms such as the Standard Degradation or
Simple Extrapolation. Table 2 represents the error
rate for the brake wear degradation after some
flights when there is a checking in an operational
plan for 35 flights performed by the same aircraft:
Table 2: Error rates.
Landings
after a
checking
Standard
degradation
Simple
extrapolation
PhysicalB
N
3 -0.1243 -0.0465 0.1157
12 -2.567 -1.2804 0.213
20 -14.0901 -4.2572 0.099
The difference between conventional models and
Bayesian Network is evident. Standard Degradation
and Simple Extrapolation have major error rate and
they increase quickly over the time, whereas
PhysicalBN which represents the physical model
when data is available improves the results and
unlike conventional models it does not perform
estimations superior to the real degradation. But
PhysicalBN does not fit with the prognosis because
its input parameters such as aircraft weight or
landing velocity are not available before the landing.
In this case, the results of the PhisycalBN would be
the same as the Standard Degradation’s. Even so,
PhysicalBN provides with confidence levels of the
brake wear degradation.
Nevertheless, OpBN overcame this problem
using operational plan information in order to
estimate input parameter for the PhysicalBN. The
evaluation of OpBN is more complex as the
goodness of the model depends on the accuracy of
the probabilities that link the information of the
operational parameter with the input parameters of
the PhysicalBN.
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
574

Even though Bayesian Networks give good
results compared to the current existing techniques,
there is still the possibility to improve them. A new
network is been adjusted. The first idea is that the
network will be able to adjust its probabilities faced
with the arrival of new data after some flights.
6 CONCLUSIONS
Conditional View function is an important task for
operational support and operational risk assessment
for aerospace industry. This function involves many
types of aircraft components (brake wear, electronic
components, actuators, fuel pump, etc) to be
evaluated.
Because of the fact that is not possible to achieve
this task with an only type of technique it is
necessary to look for different techniques which
involve many issues that lead to the need to cope
with uncertainties, and the need to re-assess and
adapt initial models.
Bayesian Networks are useful technologies.
Even tough most of the efforts so far have been
focused on diagnosis for Bayesian Networks, this
paper demonstrates the usage concerning prognosis,
in particular for the Conditional View in order to
improve aircraft maintenance with a new type of
decision support.
ACKNOWLEDGEMENTS
The authors gratefully acknowledge the support of
the European Commission Sixth Framework
program for Research and Technological
Development. This paper summarizes work
performed as part of FP6 project TATEM
"techniques and technologies for new maintenance
concepts" (Integrated Project AIP3-CT-2004-
502909).
The authors also acknowledge the support of
Brian Bbell and Bert Bullen of BAE Systems for
their support on the provision of data for the Brake
Wear use case.
REFERENCES
Byington, C.S, Roemer, M.J, Galie, T., 2002. “Prognostic
enhancements to diagnostic systems for improved
condition-based maintenance”. Aerospace Conference
Proceedings. IEEE Publication. Vol 6, 2815-2824.
Díez, F. J., 2000. “Introduction to Approximate
Reasoning”. In Spanish. PhD Course, UNED, Madrid.
Gilabert, E., Arnaiz, A., 2006. “Intelligent automation
systems for predictive maintenance. A case study”.
Robotics and Computer Intergrated Manufacturing
(RCIM). Vol22 numbers 5-6. pp543-549.
Dietterich, T., 1999. “Learning in Graphical Models”.
First MIT Press edition.
Neapolitan, R.E., 2004. “Learning Bayesian Networks”.
Pearson Prentice Hall.
Goode, K.B., Roylance, B., 1999. “Predicting the Time to
Failure of Critical Components- A Software Package
Strategy”. Proc. Condition Monitoring and diagnostic
engineering management (COMADEM) 99 pp. 547-
555.
Onisko, A., Druzdzel, M. J., Wasyluk, H., 1998. “A
probabilistic Causal Model for Diagnosis of Liver
Disorders”. Intelligent Information Systems VII.
Proceedings of the Workshop held in Malbork,
Poland, June 15-19.
Sierra, B., Larrañaga, P., 1998. “Predicting survival in
malignant skin melanoma using Bayesian Networks
automatically induced by genetic algorithms. An
empirical comparison between different approaches.”
Artificial intelligence in Medicine, 14:215-230.
Lazkano, E., Sierra, B., Astigarraga, A., Martínez-Otzeta,
J.M., 2007. “On the use of Bayesian Networks to
develop behaviours for mobile robots” Robotics and
Autonomus Systems 55 (2007) 253-265.
Ibargüengoytia, P. H., Vadera, S., Sucar, L. E., 2006. “A
Probabilistic Model for Information and Sensor
Validation”. The Computer Journal 2006 49(1):113-
126.
Doguc, O., Ramirez-Marquez, J. E., 2009. “A generic
method for estimating system reliability using
Bayesian networks”. Reliability Engineering and
System Safety 94 (2009) 542-550.
Oukhellou, L., Come, E., Bouillaut, L., Aknin, P., 2008.
“Combined use of sensor data and structural
knowledge processed by Bayesian network:
Application to a railway diagnosis aid scheme”.
Transportatino Research Part C 16 (2008) 755-767.
Barco, R., Díez, L., Wille, V., Lázaro, P., 2009.
“Automatic diagnosis of mobile communication
networks under imprecise parameters”. Expert
Systems with Applications 36 (2009) 489-500.
IMPROVING AIRCRAFT MAINTENANCE WITH INNOVATIVE PROGNOSTICS AND HEALTH MANAGEMENT
TECHNIQUES - Case of Study: Brake Wear Degradation
575
