
IMPROVING THE PERFORMANCE OF CODEQ
USING QUADRATIC INTERPOLATION
Mahamed G. H. Omran
Department of Computer Science, Gulf University for Science and Technology, Kuwait
Ayed Salman
Computer Engineering Department, Kuwait University, Kuwait
Keywords: Metaheuristics, Opposition-based Learning, Chaotic Search, Differential Evolution, Quadratic Interpolation.
Abstract: CODEQ is a new, population-based meta-heuristic algorithm that is a hybrid of concepts from chaotic
search, opposition-based learning, differential evolution and quantum mechanics. CODEQ has successfully
been used to solve different types of problems (e.g. constrained, integer-programming, engineering) with
excellent results. In this paper, a new mutated vector based on quadratic interpolation (QI) is incorporated
into CODEQ. The proposed method is compared with the original CODEQ and a differential evolution
variant the uses QI on eleven benchmark functions. The results show that using QI improves both the
efficiency and effectiveness of CODEQ.
1 INTRODUCTION
CODEQ (Omran 2009) is a new, parameter-free
meta-heuristic algorithm that is a hybrid of concepts
from chaotic search, opposition-based learning
(Tizhoosh 2005), differential evolution (DE) (Storn
and Price 1995) and quantum mechanics. The
performance of CODEQ was investigated and
compared with other well-known population-based
optimization approaches (e.g. DE and Particle
swarm optimization (Kennedy and Eberhart 1995))
when applied to eleven benchmark functions
(Omran 2009). The results show that CODEQ
provides excellent results with the added advantage
of no parameter tuning. In addition, the application
of CODEQ to constrained problems was
investigated by Omran and Salman (2009) with
encouraging results. Furthermore, CODEQ was
successfully used to solve integer programming
problems (Omran and al-Sharhan 2009).
Quadratic interpolation (QI) (Mohan and
Shanker 1994) is a nonlinear operator that uses three
solutions to generate a new solution lying at the
point of minima of the quadratic curve passing
through the three chosen solutions. QI has been
successfully used to improve the performance of DE
(Pant et al. 2008) and PSO (Pant et al. 2007). In this
paper, we investigate the effect of using QI with
CODEQ. Eleven well-known benchmark problems
are used to compare the proposed approach against
the original CODEQ and the method proposed by
Pant et al. (2008).
The reminder of the paper is organized as
follows: Section 2 provides an overview of CODEQ.
The proposed method is presented in Section 3.
Benchmark functions to measure the performance of
the different approaches are discussed in Section 4.
Results of the experiments are presented in Section
5. Finally, Section 6 concludes the paper.
2 CODEQ
The CODEQ algorithm (Omran 2009) works as
follows:
Step 1. A population of s vectors are randomly
initialized within the search space.
Step 2. For each parent, , of iteration t, a trial
vector, , is created by mutating the parent
vector. Two individuals , and are
randomly selected with i
1
≠ i
2
≠ i, and the difference
265
G. H. Omran M. and Salman A. (2010).
IMPROVING THE PERFORMANCE OF CODEQ USING QUADRATIC INTERPOLATION.
In Proceedings of the 2nd International Conference on Agents and Artificial Intelligence - Artificial Intelligence, pages 265-270
Copyright
c
SciTePress

vector, - , is calculated. The trial vector is
then calculated as
v
i
(t) x
i
(t) (x
i
1
(t) - x
i
2
(t))ln 1/ u
(1)
where u ~ U(0,1).
The generated offspring,
v
i
(t)
, replaces the
parent,
x
i
(t)
, only if the fitness of the offspring is
better than that of the parent (i.e. apply greedy
selection).
Step 3. For each iteration t, a new vector is created
as,
w t
L U r x
b
t if U 0,1 0.5
x
g
t x
i
1
t x
i
2
t 2c t 1
otherwise
(2)
where r ~ U(0,1), L and U are the lower and upper
bounds of the problem’s variables, x
b
(t) is the worst
(i.e. least fit) vector in iteration t, x
g
(t) is the best
(i.e. fittest) vector in iteration t,
x
i
1
(t)
, and
x
i
2
(t)
are randomly selected vectors with i
1
≠ i
2
≠ i and c(t)
is a chaotic variable defined as,
c t
c t 1 p c t 1 (0, p)
1 c t 1
1 p
c t 1 [p,1)
where c(0) and p are initialized randomly within the
interval (0,1).
Step 4. The generated vector,
w
i
(t)
, replaces the
worst vector in iteration t,
x
b
(t)
, only if the fitness
of
w
i
(t)
is better than that of
x
b
(t )
.
Step 5. Repeat steps 2-4 until a stopping criterion is
satisfied.
For more details about CODEQ, the interested
reader is referred to Omran (2009).
3 THE PROPOSED METHOD
The quadratic interpolation (QI) uses the best
solution found so far and two other solutions from
the population to determine a new solution lying at
the point of minima of the quadratic curve passing
through them. In Pant et al (2007; 2008), two
randomly chosen solutions were used along with the
best solution. In this paper, the individual solution
itself is used along with the best solution and a
randomly chosen solution. The rationale behind this
modification is that including the individual itself
induces an intensification of the search in the
vicinity of the vector itself (i.e. local search), while
the global best solution focuses on global
intensification that improves the quality of the
solutions generated. Adding a new solution adds
useful information that significantly improves
overall performance (Yin et al. 2009).
In the proposed algorithm, called CODEQ-QI,
step 2 in CODEQ is modified as follows:
For each vector, , in the
population
If (U(0,1) P
QI
) /* Use quadratic
interpolation */
v
i
t 0.5
x
i
2
t x
i
1
2
t
f x
g
t
x
i
1
2
t x
g
2
t
f x
i
t
x
g
2
t x
i
2
t
f x
i
i
t
x
i
t x
i
1
t
f x
g
t
x
i
1
t x
g
t
f x
i
t
x
g
t x
i
t
f x
i
i
t
else /* Use Eq. 1 */
v
i
(t ) x
i
(t) (x
i
1
(t ) - x
i
2
(t))ln
1
u
Endif
Endfor
In the above, P
QI
is a user-specified parameter
representing the probability of applying the QI
operator, g is the index of the best solution found so
far, , and
are randomly chosen
vectors where i
1
≠ i
2
≠ i.
The QI operator helps in finding better solutions
and enhancing the explorative capabilities of
CODEQ by looking for solutions lying between
three chosen vectors (Pant et al. 2008). All the other
steps in CODEQ remain intact.
4 BENCHMARK FUNCTIONS
Eleven functions have been used to compare the
performance of CODEQ-QI with that of other
methods. These benchmark functions provide a
balance of unimodal, multimodal, separable, non-
separable and noisy functions.
Sphere, Rosenbrock and Rotated hyper-ellipsoid
are unimodal, while the Step function is a
discontinuous unimodal function. The Quartic
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
266

Table 1: Results of CODEQ and CODEQ-QI algorithms (D=30). The average and standard deviation (in parenthesis) of the
number of function evaluations are shown in italic (between square brackets).
CODEQ
CODEQ-QI
Sphere
1.0162e-18(3.7317e-18)
[20740.7(2683.674015)]
3.1080e-31(1.6615e-30)
[12641.9(1589.139614)]
Camel Back
-1.031628(0)
[4461.5(725.928074)]
-1.031628(0)
[1748.3(460.297591)]
Rosenbrock
26.220137(0.647238)
[50000(0)]
21.732962(0.740005)
[50000(0)]
Step
0(0)
[5977.9(3111.437702)]
0(0)
[3985.5(1619.979709)]
Quartic function
9.8307e-04(8.3342e-04)
[50000(0)]
8.7277e-04(4.1858e-04)
[50000(0)]
Rotated hyper-ellipsoid
2.2595e-08(4.4983e-08)
[38257.5(5657.586032)]
3.7291e-15(1.1353e-14)
[22342.1(3210.705996)]
Rastrigin
0(0)
[21572.0(2746.662639)]
0(0)
[15588.0(1360.410283)]
Ackley
1.4585e-10(1.8038e-10)
[31914.8(3205.647252)]
8.8818e-16(0)
[17354.3(5654.812135)]
Griewank
0(0)
[19882.2(2842.014031)]
0(0)
[12388.6(1743.796465)]
Salomon
3.0882e-04(0.0012)
[48394.633333(2756.866255)]
9.3422e-08(5.0485e-07)
[38533.666667(4519.078845)]
Normalized Schwefel
-413.6818(27.4813)
[45003.466667(7553.827788)]
-418.5922(1.1923)
[31911.066667(9817.485808)]
function is a noisy function. Rastrigin, Ackley,
Griewank, Salomon and Normalized Schwefel are
difficult multimodal functions where the number of
local optima increases exponentially with the
problem dimension. The Camel-Back function is a
low-dimensional function with only a few local
optima. For more details regarding these functions,
interested reader is referred to (Omran and
Englebrecht 2009).
5 EXPERIMENTAL RESULTS
This section compares the performance of CODEQ-
QI with that of the original CODEQ (Omran 2009)
and DE-QI (Pant et al. 2008) algorithms.
Performance is measured in terms of effectiveness
and efficiency. For the DE-QI, F = 0.5, p
r
= 0.5 and
P
QI
= 0.1 as suggested in Pant et al. (2008). For
CODEQ-QI, P
QI
= 0.1 as recommended in Pant et al.
(2008). The results reported in this section are
averages and standard deviations over 30
simulations. Each simulation was allowed to run for
50,000 evaluations of the objective function using a
population size of 50 individuals (i.e. s = 50). All
functions were implemented in 30 dimensions
except for the two-dimensional Camel-Back
function. The statistically significant best solutions
have been shown in bold (using the non-parametric
statistical test called Wilcoxon’s rank sum test for
independent samples (Wilcoxon 1945) with α =
0.05).
All the tests are run on an Apple MacBook
computer with Intel Core Due 2 processor running at
2.0 GHz with 2GB of RAM. Mac OS X 10.5.6 is the
operating system used. All programs are
implemented using MATLAB version 7.6.0.324
(R2008a) environment.
5.1 Effectiveness
Performance effectiveness is measured ―in terms of
the mean best solution quality that can be obtained
by a competing algorithm when both algorithms runs
for a specified maximum number of function
evaluations‖(Yin et al. 2009). Table 1 summarizes
the results obtained by applying CODEQ and
CODEQ-QI to the benchmark functions. The results
show that CODEQ-QI outperformed CODEQ in
seven out of eleven benchmark functions. In the
remaining four functions, both CODEQ and
CODEQ-IQ reached the global optimum solution.
IMPROVING THE PERFORMANCE OF CODEQ USING QUADRATIC INTERPOLATION
267
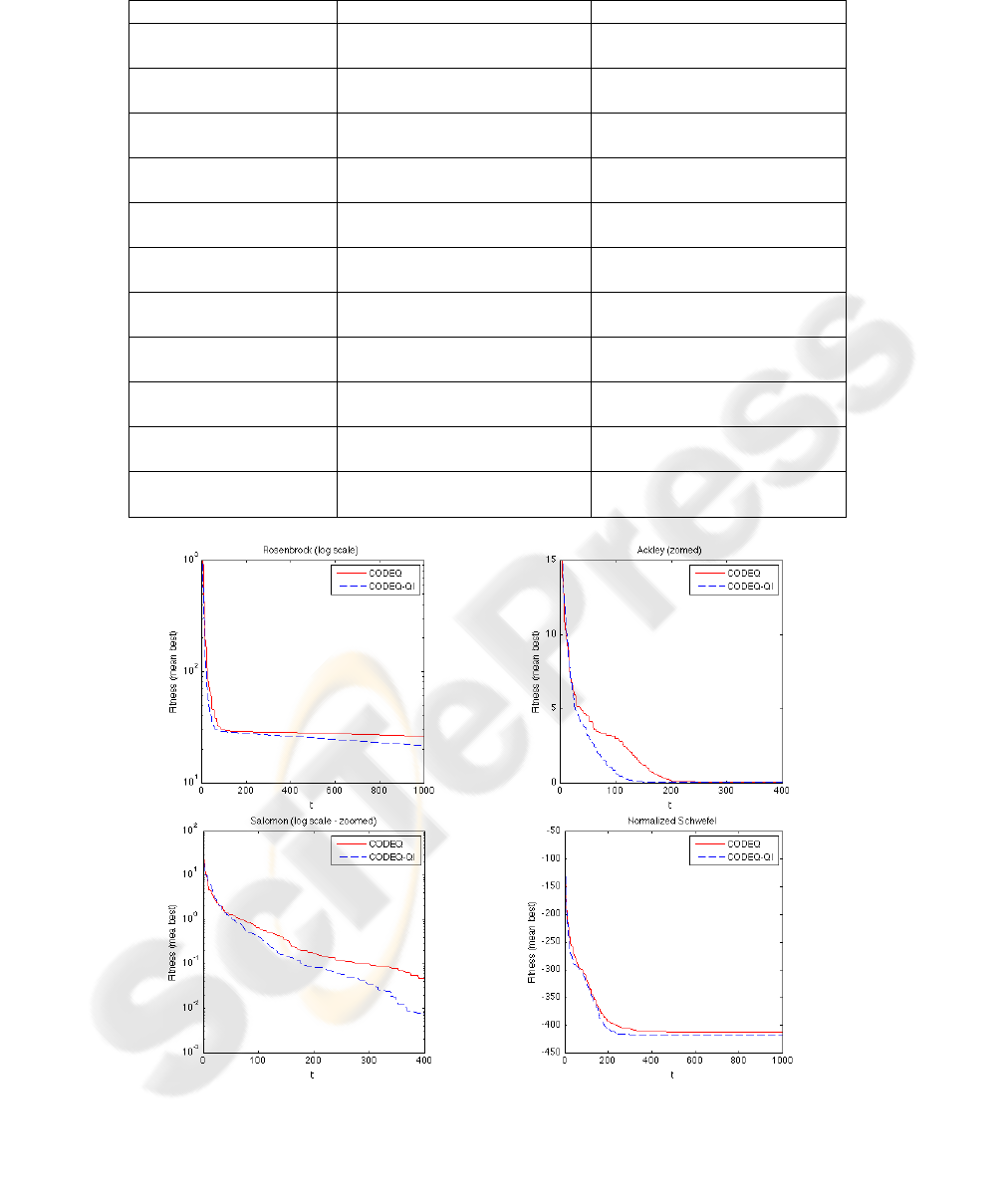
Table 2: Results of DE-QI and CODEQ-QI algorithms (D=30). The average and standard deviation (in parenthesis) of the
number of function evaluations are shown in italic (between square brackets).
DE-QI
CODEQ-QI
Sphere
5.1719e-19(3.3093e-19)
[23300(411.682837))]
6.0092e-33(1.4112e-32)
[11858.2(1553.313642)]
Camel Back
-1.031628(0)
[1596.666667(292.708321)]
-1.031628(0)
[1617.4(343.278674)]
Rosenbrock
25.671742(0.369040)
[50000(0)]
21.705992(0.531362)
[50000(0)]
Step
0(0)
[10133.333333(356.064052)]
0(0)
[4051.8(1566.423235)]
Quartic function
0.008695(0.003032)
[50000(0)]
0.000712(0.000479)
[50000(0)]
Rotated hyper-ellipsoid
7318.220555(2683.290797)
[50000(0)]
1.1695e-15(2.3274e-15)
[22024.2(3802.027521)]
Rastrigin
119.363797(9.357981)
[50000(0)]
0(0)
[15089.9(1694.940246)]
Ackley
1.7370e-10(7.0892e-11)
[33556.666667(573.965837)]
8.8818e-16(0)
[19156.3(5045.179031)]
Griewank
0(0)
[24531.666667(941.063534)]
0(0)
[12902(1639.730613)]
Salomon
0.189943(0.030300)
[50000(0)]
2.5158e-08(1.0696e-07)
[39236.7(4189.038925)]
Normalized Schwefel
-352.316511(7.430610)
[50000(0)]
-418.472872(2.793468)
[31301.866667(8886.902279)]
Figure 1: Comparison between CODEQ and CODEQ-QI for selected benchmark problems. The vertical axis represents the
average best function value and the horizontal axis represents the number of generations.
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
268

Figure 2: Comparison between DE-QI and CODEQ-QI for selected benchmark problems. The vertical axis represents the
average best function value and the horizontal axis represents the number of generations.
Similarly, Table 2 shows the results obtained by
applying DE-QI and CODEQ-QI to the benchmark
functions. The results show that CODEQ-QI
outperformed DE-IQ in eight out of eleven
functions. On the remaining three functions both
approaches reached the global optimum solution.
Note that, Omran (2009) showed that CODEQ
outperformed PSO, DE and other algorithms on the
same set of benchmark functions. Thus, it can be
concluded that CODEQ-QI outperforms these
approaches on the examined set of benchmark
functions.
5.2 Efficiency
The number of function evaluations (FEs) required
to reach an error value less than 10
-6
(provided that
the maximum limit is 50,000 FEs) was recorded in
the 30 runs and the mean and standard deviation of
FEs were calculated and shown in Tables 1 and 2
between brackets. FEs can be used to compare the
convergence speed (i.e. the efficiency) of the
different methods. A smaller FE means higher
convergence speed. On the other hand, having FEs
equal to 50,000 indicates that the approach cannot
converge to the global optima. Tables 1 and 2 show
that CODEQ-QI generally reached good solutions
faster than (or equal to) the other approaches in all
the benchmark functions (except for the Camel back
function when DE-QI performed better). Figures 1
and 2 illustrate results for selected functions. The
figures show that CODEQ-QI reached good
solutions faster than the other approaches.
6 CONCLUSIONS
In this paper, we investigated the effect of
embedding a quadratic interpolation (QI) operator
into CODEQ. The proposed method, CODEQ-QI,
was compared against CODEQ and DE-QI on
eleven benchmark functions. The results showed that
QI significantly improved the performance of
CODEQ (in terms of both efficiency and
effectiveness).
Future work will study the effect of P
QI
on the
performance of CODEQ-QI. In addition, the
performance of CODEQ-QI when applied to real
engineering optimization problems needs to be
investigated.
IMPROVING THE PERFORMANCE OF CODEQ USING QUADRATIC INTERPOLATION
269

REFERENCES
Kennedy, J., Eberhart, R., 1995. Particle Swarm
Optimization. In Proceedings of IEEE International
Conference on Neural Networks, Perth, Australia, vol.
4, pp. 1942-1948.
Mohan, C., Shanker, K., 1994. A Controlled Random
Search Technique for Global Optimization using
Quadratic Approximation. Asia-Pacific Journal of
Operational Research, vol. 11, pp. 93-101.
Omran, M., 2009. CODEQ: An Effective Meta-heuristic
for Continuous Global Optimization. Under revision.
Omran, M., al-Sharhan, S., 2009. Optimization of Discrete
Values using Recent Variants of Differential
Evolution. In the proceedings of the 4
th
IASTED
international Conference on Computational
Intelligence, Hawaii, USA.
Omran, M., Engelbrecht, A., 2009. Free Search
Differential Evolution. Accepted for publication in
proceedings of the IEEE Congress on Evolutionary
Computation (CEC’2009), Norway.
Omran, M., Salman, A., 2009. Constrained Optimization
using CODEQ. Chaos, Solitons & Fractals Journal,
Elsevier, vol. 42(2), pp. 662-668.
Pant, M., Thangaraj, R., Singh, V., 2007. A New Particle
Swarm Optimization with Quadratic Interpolation. In
proceedings of the International Conference on
Computational Intelligence and Multimedia, India,
vol. 1, pp. 55-60.
Pant, M., Thangaraj, R., Singh, V., 2008. A New
Differential Evolution Algorithm for Solving Global
Optimization Problems. In the proceedings of the
International Conference on Advanced Computer
Control, Thailand, pp. 388-392.
Storn, R., Price, K., 1995. Differential Evolution – A
Simple and Efficient Adaptive Scheme for Global
Optimization over Continuous Spaces. Technical
Report TR-95-012, International Computer Science
Institute, Berkeley, CA.
Tizhoosh, H., 2005. Opposition-based Learning: A New
Scheme for Machine Intelligence. In Proceedings Int.
Conf. Comput. Intell. Modeling Control and Autom,
vol. I, pp. 695—701.
Wilcoxon, F., 1945. Individual Comparisons by Ranking
Methods. Biometrics, vol. 1, pp. 80-83.
Yin, P., Glover, F., Laguna, M., Zhu, J., 2009. Cyber
Swarm Algorithms – Improving particle swarm
optimization using adaptive memory strategies.
European Journal of Operation Research,
doi:10.1016/j.ejor.2009.03.035.
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
270
