SVM EVALUATION FOR BRAIN COMPUTER INTERFACE

SYSTEMS

Mario Salerno, Giovanni Costantini, Daniele Casali

Giancarlo Orengo, Pietro Cavallo, Giovanni Saggio

Dipartimento di Ingegneria Elettronica, Università di Roma “Tor Vergata”, Rome, Italy

Luigi Bianchi, Lucia Quitadamo, Maria Grazia Marciani

Dipartimento di Neuroscienze, Università di Roma “Tor Vergata”, Rome, Italy

Keywords: Support Vector Machine, Classification, Brain computer interface.

Abstract: A Support Vector Machine (SVM) classification method for data acquired by EEG registration for

brain/computer interface systems is here proposed. The aim of this work is to evaluate the SVM

performances in the recognition of a human mental task, among others. Such methodology could be very

useful in important applications for disabled people. A prerequisite has been the developing of a system

capable to recognize and classify the following four tasks: thinking to move the right hand, thinking to

move the left hand, performing a simple mathematical operation, and thinking to a nursery rhyme. The data

set exploited in the training and testing phases has been acquired by means of 61 EEG electrodes and

consists of several time series. These time data sets were then transformed into the frequency domain, in

order to obtain the power frequency spectrum. In such a way, for every electrode, 128 frequency channels

were obtained. Finally, the SVM algorithm was used and evaluated to get the proposed classification.

1 INTRODUCTION

Brain electrical activity can be observed and

recorded by placing a set of ad-hoc wet electrodes

on the surface of the scalp. Every kind of task or

thought performed by the human being causes

electrical activity in different parts of the brain; thus,

the activity recognition could be considered as a

desirable machine learning application. The task is

not very trivial because of many reasons. First, the

states of all neurons in the brain are unknown,

except the mean values of them in some zones of the

outer part of the brain. Second, the electrical activity

is not limited to a single zone, depending on the task

the subject is performing: in some cases, it can even

involve the whole brain and the difference among

different tasks seems consist in the way the electrical

waves are moving from one zone to another. A third

problem concerns the base of the brain electrical

activity, even presents when no thoughts or

movements are done. So the base activity, including

breathing and all involuntary movements, can mask

the voluntary task we intend to detect. The “noise

signals” corresponding to this base activity can also

assume higher levels with respect to those of

“voluntary signals” under detection.

Stand the above considerations, the main

challenge consists in the proper classification of the

dataset collected from the electrodes, in order to

recognize the mental task the subject was

performing.

Though the classical classification method for

this kind of data makes use of artificial neural

networks (ANN) (Huan, 2004), a different kind of

classifier is here proposed. In fact we want to

evaluate how and if the Support Vector Machines

(SVM) can be recognized as a useful tool instead of,

together with or in addition to the classical neural

network. This because SVM presents the interesting

advantage to support datasets with a huge number of

components; in such a way, the need of reduction of

the feature space is not more necessary otherwise

than ANN. In addition, in the present application,

SVM training algorithm furnishes valuable

advantages with respect to the “back-propagation”, a

rule usually applied in the ANN approach.

In the following sections, the acquisition data

system, the acquired data pre-processing and the

240

Salerno M., Costantini G., Casali D., Orengo G., Cavallo P., Saggio G., Bianchi L., Quitadamo L. and Grazia Marciani M. (2010).

SVM EVALUATION FOR BRAIN COMPUTER INTERFACE SYSTEMS.

In Proceedings of the Third International Conference on Bio-inspired Systems and Signal Processing, pages 240-244

DOI: 10.5220/0002721802400244

 SciTePress

classifier will be presented. Experimental tests and

related results will be the test bench to validate the

proposed method.

EEG

Pre

rocessin

Classificatio

Figure 1: Block-diagram of the sensor system.

2 ACQUISITION DATA SYSTEM

The overall system consists in three blocks (Fig. 1),

namely data acquisition, pre-processing, and

classification.

Figure 2: Position and names of the electrodes.

The acquisition data system used 61 Ag-AgCl

scalp electrodes. The electrodes were located

according to the International 10-20 system (Huan,

2004; Wolpaw, 2002; Schogl, 2005; Yoo, 2004;

Sharbrough, 1991; Blankertz, 1970) as shown in Fig

The electrodes were connected to the computer

by fiber optic transmission channels, in order to

provide the proper electrical insulation and to

guarantee the subject by any risk of electrical shock.

The signals were processed at the sampling rate

of 256 Hz and band-pass filtered in the band from

0.5 Hz to 128 Hz. The sensitivity of the amplifier is

set to 4 mV. The picture of the sensor system is

shown in Fig. 3.

Figure 3: Picture of the sensor system.

3 PREPROCESSING

The frequencies of the waves observed in EEG

signals are usually related to different kinds of brain

activity. To this purpose, some classical waves have

been defined, namely alpha waves (8-12 Hz), beta

waves (12-19 Hz), gamma waves (around 40 Hz)

and delta waves (1-4 Hz) that are associated to

weakness, sleep, REM and other kinds of brain

states respectively (Blankertz, 2006; Brazier, 1970;

Ward, 2006).

Following this approach, the acquired dataset

was analysed in the frequency domain. In

correspondence to every task, the FFT algorithm

was applied to three windows of 256 samples and,

for each window, the ratio between the mean value

of alpha waves (8-12 Hz) and the mean value in

frequencies range (5-40 Hz) was evaluated. Only the

first half of every FFT window was considered since

the second half is symmetric and couldn’t give any

further information. Channels from 1 to 127

represent the frequencies from 1 to 127 Hz. Zero

frequency (Channel 0) was omitted. In this way, one

data point was obtained in correspondence to every

electrode and to every task to be classified. In order

to obtain a useful comparison between different

choices of electrodes, three occurrences were

considered. The first one corresponded to all the

electrodes. The second one considered a proper

selection of 19 electrodes, in particular the

electrodes: C

, C

, P

, T

, F

, O

. These electrodes are

strictly related to the sensory-motory cortical area

(related to hand moving), and to the lower parietal

(related to arithmetical operations). In the third

occurrence, the electrodes C

and C

were under

consideration, being very useful to discriminate right

hand vs. left hand, as suggested in (Blankertz, 2006),

SVM EVALUATION FOR BRAIN COMPUTER INTERFACE SYSTEMS

241

but also the electrodes around the above ones were

used, namely C

, C

, FC

Thus, in this case, a total set of 10 electrodes was

used.

As a final step, since a large variance in the

numerical values was registered, a normalization

rule was necessary, so that all the values involved be

in the interval form 0 to 1.

4 CLASSIFIER

In the latest years, the technical literature proved the

SVM to play a valid alternative rule to multi-layer

feed-forward neural networks, for data classification

and regression or PCA (Jolliffe, 2002; Burges,

1998). The basic formulation of SVM learning rule

for classification consists in the minimum norm

solution of a set of linear inequality constraints. It

seems useful to remark the relation between these

two paradigms in order specify some peculiar

properties of SVM rule: the “optimal” margin of

separation, the robustness of the solution and the

availability of efficient computational tools. Indeed,

SVM learning problem does not get to non-global

solutions and can be solved by standard routines for

Quadratic Programming (QP). In the case of a large

amount of data, some fast solvers for SVMs are

available, e.g. SVM-light (Joachims, 1999;

Scholkopf, 1999). In the following subsection, a

short description of an SVM will be given.

4.1 Support Vector Machines

Let (x

, y

), k = 1,…, m represent the training

examples for the classification problem; each

example x

∈R

belongs to the class y

∈{-1, +1}.

Assuming linearly separable classes, a separating

hyper-plane will exist, such that

+ b) > 0 k = 1,…, m (1)

The minimum distance between the data points

and the separating hyper-plane is the separation

margin. The goal of an SVM is to maximize this

margin. If the weights w and the bias b are rescaled,

the constraints (1) can be rewritten as

+ b) ≥ 1 k=1,…,m (2)

Thus, the margin of separation is equal to 1/||w||

and the maximization of the margin is equivalent to

the minimization of the Euclidean norm of the

weight vector w. The corresponding weights and

bias represent the optimal separating hyper-plane

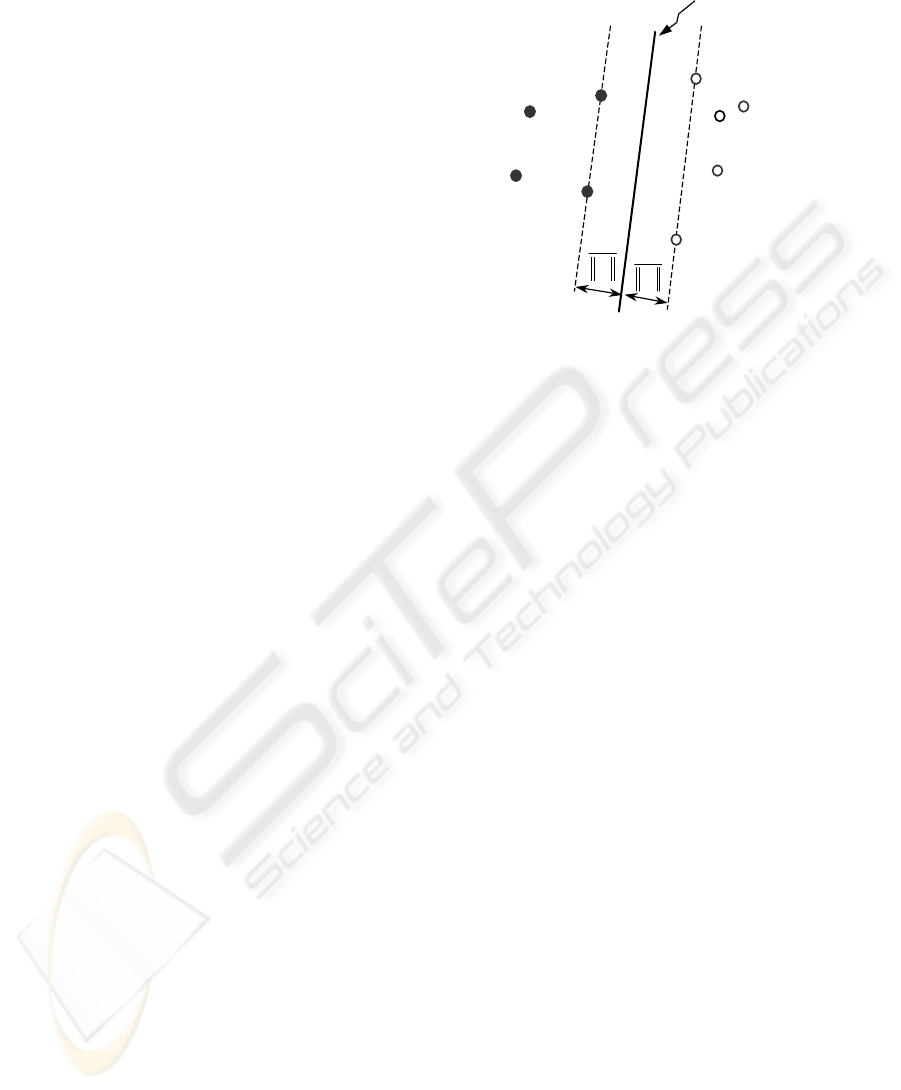
(Fig. 4).

= +1

= -1

optimal

hyperplane

Figure 4: Optimal separating hyper-plane corresponding to

the SVM solution. The support vectors lie on the dashed

lines.

5 EXPERIMENTS AND RESULTS

In the experiments, five mentally healthy subjects

(three males and two females) were involved for two

days. Each subject performed two sessions every

day. During a single session, each subject was asked

to perform 400 tasks, randomly selected among the

following ones: thinking to move the right hand,

thinking to move the left hand, performing a simple

mathematical operation, and thinking to a nursery

rhyme.

Two sessions on distinct days were recorded for

each subject. Each session consisted of 200 trials (50

for each of the four possible tasks).

The subjects sat in a comfortable armchair in

front of a computer screen. For every trial a text,

indicating the task to perform, appeared on the black

screen for 3 sec. The Inter Trial Interval (ITI) was

set to 1 sec.

The objective was to operate discrimination

between the following pairs of tasks: left hand vs.

right hand, and mathematical operation vs. nursery

rhyme. The whole dataset was spitted into training

set (60% of the dataset), validation set (15% of the

dataset) and test set (20% of the dataset). The

accuracy results for the test set on Nursery rhyme vs.

Math operation are shown on Table 1 for every

subject, while the mean values are reported on the

bottom line. The accuracy results for the test set on

Right hand vs. Left hand are shown on Table 2.

BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing

242

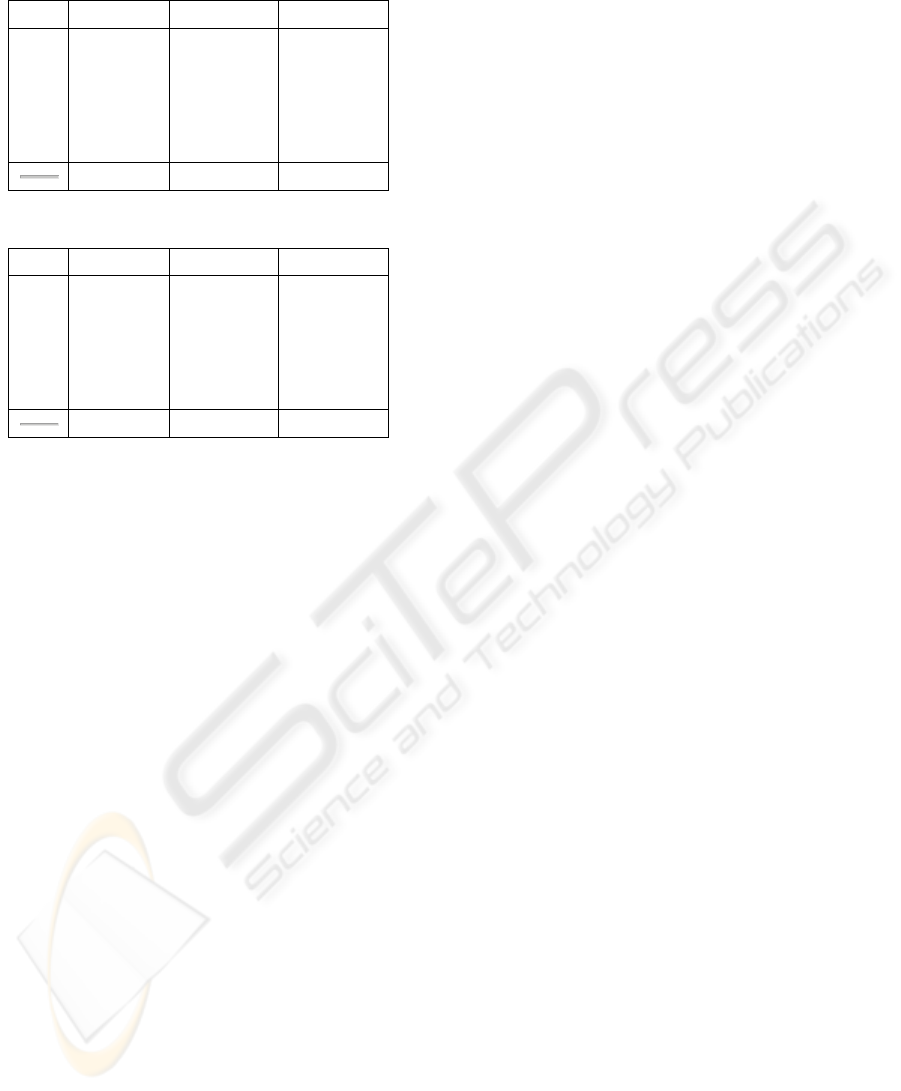
Table 1: Math vs. Nursery rhyme discrimination accuracy

results.

Subj. 61 elect. 19 elect. 10 elect.

1 75.8% 78.3% 61.5%

2 56.7% 63.3% 62.5%

3 59.2% 68.3% 53.3%

4 63.3% 73.3% 55.0%

5 73.3% 75.0% 70.8%

65.7% 71.7% 60.6%

Table 2: Left vs. Right discrimination accuracy results.

Subj. 61 elect. 19 elect. 10 elect.

1 72.5% 90.0% 75.0%

2 55.8% 76.7% 51.7%

3 55.8% 65.0% 50.8%

4 45.0% 58.3% 63.3%

5 53.4% 73.3% 63.3%

56.5% 72.6% 60.8%

For each subject (denoted with a number, for the

take of privacy), the mean values of results were

computed for two different sessions, considered

separately. No mixing of data was allowed from

different subjects, or from different sessions for the

same subject, as the results appear very different.

The accuracy in the case of usage of all the 61

electrodes is shown in the first column of the tables:

for some subject, as subject 1, it appears very high,

while it can be extremely low for some other

subjects. For instance, for subject 4 in table 2, it is

less than 50%: in this case, it could mean that,

paradoxically, a random selection between the two

choices would have given better results.

In the second column, the accuracy in the case of

19 electrodes is shown. As discussed above, an

accurate selection of best electrodes was done, in

function of the cortical areas mainly involved in the

four tasks of interest. Best results were carried out in

this case, obtaining accuracies over 70%. An error of

about 27% - 28% can be considered quite low,

accounting for the difficulty involved in the

experiment of interest: indeed, in every case, the

subject was required not to move any muscle, but

just to think of moving it. By the way, if a limb is or

is going to be really moved, the electrical activity in

the brain would become much more clear and could

be easily detected, as is shown in (Blankertz, 2006).

The accuracy in the cases of 10 electrodes is

shown in the third column. Presently, the number of

electrodes taken into account appears not sufficient

to get to good results. In particular, results appear

not useful for the discrimination between

mathematical operation and nursery rhyme, since the

selected electrodes are all around C

and C

, which

are mainly related to hand movements.

6 CONCLUSIONS

A classification method for brain-computer interface

is presented, which was able to discriminate among

different kind of mental tasks performed by a

subject. The method is based on a SVM classifier,

trained by the power frequency spectrum of EEG

signals coming from 61 electrodes set in the head

surface.

The experimental tests proved quite useful

results in case of 19 electrodes, while poor results

were obtained for 61 electrodes. This occurence is

likely to depend from the small number of trials, as

SVM method always requires a high number of

them, accounting for the large number of features to

be considered. In addition, large accuracy disparity

was found in the cases of different subjects: for

instance, in the case of 19 electrodes, accuracy up to

90% was obtained with subject 1, but just a little

over 58% with subject 4.

The results appear quite interesting compared

with other similar works, as in (Schogl, 2005), in

which different methods of classification are

considered. It was also shown SVM method to get

the best result, with accuracy average of about 63%.

The essential rules of the electrode number and

position are here pointed out, as they can

dramatically affect the classifier performance.

Future developments will include the time

domain analysis, in addition to the frequency

domain here examinated. It could be also interesting

to investigate the effect of data artefacts. They can

arise, for example, if the subject sometime can blink,

and this can produce noise in the EEG, getting worse

the performance of the classifier. Significant

improvements could be carried out cleaning the data

from this kind of noise.

REFERENCES

Huan N. J. and Palaniappan R., 2004. Neural network

classification of autoregressive features from

electroencephalogram signals for brain–computer

interface design. In Journal of Neural Engineering

vol. 1, 142-150.

Wolpaw J. R., Birbaumer N. McFarland D. J, Pfurtscheller

G. and Vaughan T. M. 2002. Brain-computer

SVM EVALUATION FOR BRAIN COMPUTER INTERFACE SYSTEMS

243

interfaces for communication and control. In

Clinical.Neurophysiology, vol. 113, no. 6, , pp. 767-

791.

Schogl, A. Lee F., Bischof H.and Pfurtscheller G., 2005

Characterization of four-class motor imagery EEG

data for the BCI-competition. In Journal of

NeuralEngineering, vol. 2, L14-L22.

Yoo S.S., Fairneny T., Chen N. K., Choo S. E., Panych P.,

Park H., Lee S. Y., Jolesz F. A., 2004. “Brain-

computer interface using fMRI: spatial navigation by

thoughts”, In Neuroreport. Jul 19;15(10):1591-5.

Sharbrough F, Chatrian G-E, Lesser RP, Lüders H, Nuwer

M, Picton TW., 1991. American

Electroencephalographic Society Guidelines for

Standard Electrode Position Nomenclature. In J. Clin.

Neurophysiol 8: 200-2.

Blankertz B., Dornhege G., Krauledat M., Müller K.-R.,

Kunzmann V., Losch F., Curio G., 2006. The Berlin

Brain-Computer Interface: EEG-based communication

without subject training. In Transactions On Neural

Systems And Rehabilitation Engineering, Vol. 14,

Issue 2, pp. 147-152.

Brazier, M. A. B., 1970. The Electrical Activity of the

Nervous System, Pitman, London.

Ward LM, Doesburg SM, Kitajo K, MacLean SE,

Roggeveen AB., 2006. Neural synchrony in stochastic

resonance, attention, and consciousness. In Can J Exp

Psychol. Dec;60(4):319-26.

Walker, 1999. Chambers Dictionary of Science and

Technology, Chambers Harrap Publishers, 2nd ed., p.

312, P.M.B.

Jolliffe I.T., 2002. Principal Component Analysis, 2nd ed.,

Springer, NY.

Burges C.J.C., 1998. A tutorial on support vector

machines for pattern recognition. In Data Mining and

Knowledge Discovery 2, Kluwer, 1998, pp.121-167.

Joachims T., 1999. Making large scale SVM learning

practical.

Scholkopf B., Burges C.J.C. and Smola A.J., 1999.

Advances in Kernel Methods-Support Vector

Learning, Eds, MIT Press, Cambridge, MA, 1999, pp.

169-184 (http://svmlight.joachims.org/).

BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing

244