STOCHASTIC GPU-BASED MULTITHREAD IMPLEMENTATION

OF MULTIPLE BACK-PROPAGATION

Noel Lopes

1,2

and Bernardete Ribeiro

CISUC - Center for Informatics and Systems of University of Coimbra, Portugal

UDI/IPG - Research Unit, Polytechnic Institute of Guarda, Portugal

Keywords:

Neural networks, Multiple back-propagation, Pattern recognition, GPU computing, Parallel programming.

Abstract:

Graphics Processing Units (GPUs) have evolved into a highly parallel, multi-threaded, many-core processor

with enormous computational power. The GPU is especially well suited to address pattern recognition prob-

lems that can be expressed as data-parallel computations. Thus it provides a viable alternative to the use of

dedicated hardware in the neural network (NN) ﬁeld, where the long training times have always been a major

drawback. In this paper, we propose a GPU implementation of the online (stochastic) training mode of the

Multiple Back- Propagation (MBP) algorithm and compare it with corresponding standalone CPU version and

with the batch training mode GPU implementation. For a fair and unbiased comparison we run the experiments

with benchmarks from machine learning and pattern recognition ﬁeld and we show that the GPU performance

excel the CPU results in particular for high complex problems.

1 INTRODUCTION

Driven by the insatiable market demand for real time

high-deﬁnition 3D graphics, the Graphics Processing

Unit (GPU) has evolved into a highly parallel proces-

sor with tremendous computational power (NVIDIA,

2009b). Modern GPUs, present in today computers,

offer increasing degrees of programmability allow-

ing enough ﬂexibility to be used to accelerate non-

graphics applications (Steinkrau et al., 2005). Due to

its inherent parallel architecture, GPUs offer remark-

able performance gains when compared to CPUs for

computationally-intensive applications, providing an

attractive alternative to use dedicated hardware in the

NN ﬁeld (Steinkrau et al., 2005). Recently, GPU im-

plementations of machine learning algorithms (Lopes

and Ribeiro, 2009) (Catanzaro et al., 2008) (Che

et al., 2008) show they are becoming a platform of

choice in the scientiﬁc computing community (Schaa

and Kaeli, 2009). In part this is due to the ad-

vent of general purpose programming languages such

as NVIDIA CUDA (Compute Uniﬁed Device Ar-

chitecture) that overcome many of the difﬁculties

of classic General-Purpose computation on the GPU

(GPGPU) (Che et al., 2008) (Jang et al., 2008). More-

over, GPUs are widely used by the large gaming in-

dustry and so they are relatively affordable (Catanzaro

et al., 2008). In this article we present a GPU imple-

mentation of the online (stochastic) training mode of

the Multiple Back-Propagation (MBP) algorithm and

compare its high throughput performance computing

both with the corresponding standalone CPU version

and the batch training mode GPU implementation.

The rest of the paper is organized as follows. Sec-

tion 2 introduces the CUDA programming model and

architecture. Section 3 explains the main steps of the

MBP algorithm. Section 4 presents the methodol-

ogy of its parallel GPU implementation. Section 5

describes the experimental setup and compares and

discusses the results obtained for both classiﬁcation

and regression benchmarks. Finally, section 6 sum-

marizes the contributions of this paper.

2 COMPUTE UNIFIED DEVICE

ARCHITECTURE (CUDA)

CUDA is a general purpose parallel architecture that

leverages the parallel computing engine in NVIDIA

GPUs to solve complex computational problems in a

more efﬁcient way than on a CPU. CUDA extends

271

Lopes N. and Ribeiro B. (2010).

STOCHASTIC GPU-BASED MULTITHREAD IMPLEMENTATION OF MULTIPLE BACK-PROPAGATION.

In Proceedings of the 2nd International Conference on Agents and Artiﬁcial Intelligence - Artiﬁcial Intelligence, pages 271-276

DOI: 10.5220/0002722102710276

 SciTePress

the C language, allowing programmers to deﬁne spe-

cial functions called kernels. Kernels are executed in

parallel by different CUDA threads, on a physically

separate device (GPU) that operates as a co-processor

to the host (CPU) running the program. Threads are

organized into blocks, containing up to 512 threads,

that are required to execute independently: it must be

possible to execute them in an arbitrary order either

in parallel or in series. This requirement allows the

set of thread blocks, called a grid, to be scheduled in

any order across any number of cores, enabling pro-

grammers to write code that scales with the number

of cores present on the device. Threads within a block

can cooperate among themselves by sharing data and

synchronizing their execution to coordinate memory

accesses. The number of thread blocks in a grid is

typically dictated by the size of the data being pro-

cessed rather than by the number of processors in the

system, which it can greatly exceed.

The CUDA architecture is built around a scal-

able array of multi-threaded Streaming Multiproces-

sors (SMs). Each SM has eight Scalar Processor

(SP) cores. When a program on the host invokes

a kernel grid, its blocks are enumerated and dis-

tributed to SM with available execution capacity. As

thread blocks ﬁnish their execution, new blocks are

launched on the vacated SMs. Each SM creates,

manages, and executes concurrent threads in hard-

ware with zero scheduling overhead and can imple-

ment fast barrier synchronization. Fast barrier syn-

chronization together with lightweight thread creation

and zero-overhead thread scheduling efﬁciently sup-

port very ﬁne-grained parallelism. To manage hun-

dreds of threads running several different programs,

the SM employs a new architecture called SIMT

(single-instruction, multiple-thread). The SM maps

each thread to one scalar processor core, and each

scalar thread executes independently with its own in-

struction address and register state. The SIMT unit

creates, manages, schedules, and executes threads in

groups of 32 parallel threads called warps (NVIDIA,

2009b).

3 MULTIPLE

BACK-PROPAGATION

Multiple Back-Propagation (MBP) is a generaliza-

tion of the Back-Propagation (BP) algorithm that can

be used to train Multiple Feed-Forward (MFF) net-

works (Lopes and Ribeiro, 2001). Jointly MFF net-

works and the MBP algorithm shape an architecture

that is (in most situations) preferable to the use of

feed-forward (FF) networks trained with the BP algo-

Figure 1: MFF Network. Squares represent inputs, white

circles neurons, gray circles multipliers and triangles the

bias.

rithm (Lopes and Ribeiro, 2003). MFF networks are

obtained by integrating two FF networks (a main net-

work and a space network) as shown in Figure 1. The

main network contains at least one selective activation

neuron. Selective activation neurons differentiate be-

tween stimulus (patterns). Their response depends on

the space localization of a pattern p presented to the

network and might be ampliﬁed or reduced accord-

ingly. Its output is given by (1):

= m

) = m

(

∑

j=1

+ θ

) , (1)

where y

is the output of neuron k, m

the importance

of the neuron for the network output that varies ac-

cordingly to the pattern (stimulus) presented, F

the

neuron activation function, a

its activation, θ

the

bias and w

the weight of the connection between

neuron j and neuron k. The farther from zero m

the more important becomes the k neuron contribu-

tion. On the other hand, an m

equal to zero implies

the neuron will not contribute at all to the network

output. Notice that if we consider all the m

to be

constant and equal to 1, i.e., if all neurons are equally

important to the network regardless of the presented

pattern, equation (1) becomes identical to the standard

neuron output equation. The importance (m

) of each

neuron k for the current pattern p is determined by

a standard FF network, that receives the same inputs

as the main network, named space network because

it is implicitly dividing the input space. The main

network can only calculate its outputs after knowing

the outputs (m

) of the space network. Thus the two

networks will function in a collaborative manner and

must also be trained together.

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

272

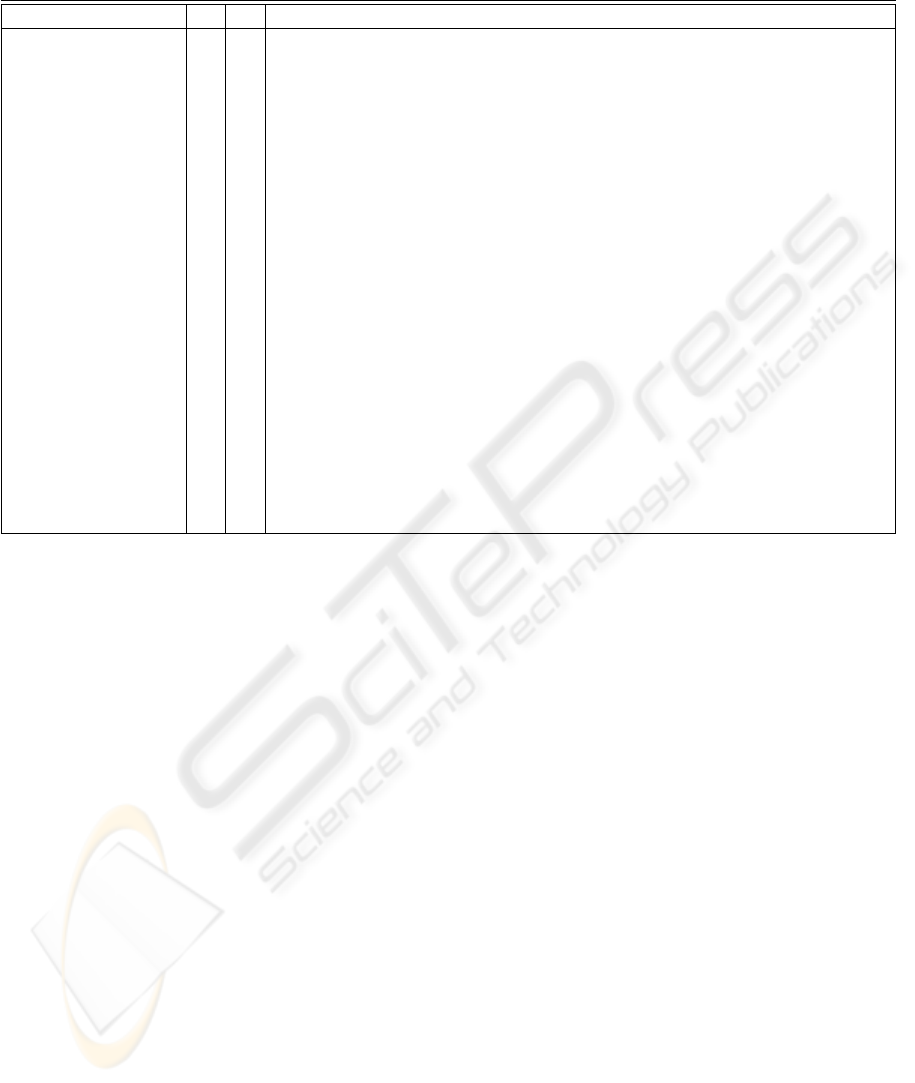
Table 1: Kernels used to implement both the BP and the MBP algorithms. The kernels used in each mode (O – online, B –

batch) are marked with an ×.

Kernel O B Purpose

FireLayer × × Calculates the outputs of all neurons in a given layer.

FireOutputLayer × × Calculates the outputs of the network output layer and the local gradients

of its neurons. If the layer contains selective activation neurons, the local

gradients of the corresponding space network neurons are also calculated.

CalcLocalGradients × × Calculates the local gradient of all neurons in a hidden layer. For selective

activation neurons, the local gradients of the corresponding space network

neurons are also calculated.

CorrectWeights × × Adjust the weights of a given layer. For the batch mode the step sizes are

also updated.

CalculateRMS × × Calculates the Root Mean Square (RMS) error of the NN.

RobustLearning × Checks if the RMS is lower than the minimum obtained so far. If so, the

minimum RMS is updated and the NN weights are stored. Otherwise, the

kernel checks whether the RMS exceeded the best RMS by a given tolerance

and in afﬁrmative case: the best weights are restored, the step sizes reduced

by a given factor and the momentum memories set to zero.

AdjustLearningRate × Randomizes the order of the patterns and then checks if the RMS is lower

than the minimum obtained so far. If so, the minimum RMS is updated

and the NN weights are stored. If not, the kernel checks whether the RMS

exceeded the best RMS by a given tolerance and in afﬁrmative case: the

best weights are restored, the step sizes reduced by a given factor and the

momentum memories set to zero. Unless the step sizes were reduced they

are then adjusted.

4 BP AND MBP PARALLEL CUDA

IMPLEMENTATION

The CUDA implementation of the batch mode for the

BP and MBP algorithms, extends the one presented

in (Lopes and Ribeiro, 2009). The current imple-

mentation has undergone a great deal of optimizations

to furthermore increase the speedups obtained, which

were already impressive (In the “two-spirals” bench-

mark, the GPU version, running on a GTX 280 de-

vice, was over 40 times faster than the CPU version).

However the main change was the addition of the ro-

bustness technique (Almeida, 1997) to complement

the adaptive step size technique already implemented.

The online implementation shares much of the

code of the batch implementation. Nevertheless there

are signiﬁcant differences in the kernel implementa-

tions and although they might have similar names,

they are optimized to the speciﬁc version. Table

1 identiﬁes the purpose of the kernels implemented

for the online and batch mode versions. The ker-

nels FireLayer, FireOutputLayer, CalcLocalGradi-

ents and CorrectWeights were designed to operate on

a generic network layer with N

neurons, each with

inputs (not including the bias) and N

output con-

nections. In the batch mode, those kernels process

(in parallel) all the N

patterns contained in the train-

ing data set, while in the online mode they process a

single pattern. Therefore in the online mode the ker-

nels must be called N

times (for each layer) in each

epoch. Although in the online mode the kernels pro-

cess a single pattern, they are actually capable of pro-

cessing several patterns in parallel. Thus they might

be used to train the NNs using small batches of pat-

terns (they could also be used to train the networks in

batch mode, but they would be inefﬁcient compared

to the kernels designed for that purpose). This imple-

mentation is sometimes referred as mini-batch where

the networks are trained using blocks of N

patterns

(1 < N

< N

5 RESEARCH DESIGN

5.1 Data Sets and Experimental Setup

The experimental setup was conducted using the

CUDA implementation (described on the previous

section) and the Multiple Back-Propagation software.

Multiple Back-Propagation is a highly optimized soft-

ware, developed in C++, for training both FF and

STOCHASTIC GPU-BASED MULTITHREAD IMPLEMENTATION OF MULTIPLE BACK-PROPAGATION

273

MFF networks with the BP and MBP algorithms.

The CPU version was benchmarked on a Intel

Core 2 6600 CPU running at 2.4 GHz, whilst the GPU

version was benchmarked on two different NVIDIA

devices: a GeForce 8600 GT with 4 SM (32 cores)

and a GTX 280 with 30 SM (240 cores).

The neural network models used in this study con-

sisted of MFF networks comprising: (i) a main net-

work containing an input layer with N

neurons, a

hidden layer with N

neurons with selective activa-

tion, an optional second hidden layer with N

neu-

rons (without selective activation) and an output layer

with N

neurons; and (ii) a space network with N

in-

puts and N

outputs.

Three benchmarks (“two-spirals”, “sonar” and

“Friedman”) were chosen for testing and comparing

the online (stochastic) and the batch parallel imple-

mentations of the MBP algorithm. The “two-spirals”

benchmark, which is considered extremely hard to

solve for algorithms of the BP family (Fahlman and

Lebiere, 1990), consists of discriminating between

the points of two distinct spirals which coil three

times around one another and the x-y plane origin.

The “sonar” benchmark

consists of discriminating

between the sonar signals bounced off a metal cylin-

der from those bounced off a roughly cylindrical rock.

The “Friedman” benchmark consists in approximat-

ing the function f (x) = 10sin(πx

)+20(x

−

)

10x

+ 5x

(Friedman, 1991).

5.2 Results and Discussion

For a fair comparison of the implementations (in both

GPU and CPU versions), the initial weights were

identical (independently of the implementation and

hardware). Table 2 shows the number of epochs

trained per minute, accordingly to the hardware used.

The number of epochs trained using the batch mode

is far superior on the GPU than on the CPU. However,

when using the online (stochastic) mode the GPU can

only achieve better results than the CPU, when the

trained NN contains a sufﬁcient large number of con-

nections. This is better emphasized in Table 3 which

shows the speedups attained by the GPU over the

CPU for both the batch and online implementations of

The latest version of Multiple Back-Propagation soft-

ware can be freely obtained at http://dit.ipg.pt/MBP.

Available at the Carnegie Mellon Univer-

sity Collection of Neural Networks Benchmarks

(http://www.cs.cmu.edu/afs/cs/project/

ai-repository/ai/areas/neural/bench/cmu/).

The training data is available at the Bilkent Univer-

sity function approximation repository (http://funapp.

cs.bilkent.edu.tr/DataSets/).

the MBP algorithm. A speedup value, S, greater than

one, means the GPU implementation is S times faster

than the corresponding CPU implementation, whilst

a speedup value smaller than one means the GPU im-

plementation is slower than the corresponding CPU

implementation. The online training mode can only

take advantage of the parallelism inherent to the NN

layers. On the other hand, the batch training mode can

also beneﬁt from the fact that each pattern can be pro-

cessed independently. Thus in the batch mode the pat-

terns can be processed in parallel, leading to greater

speedups, regardless the number of connections.

Execution pipelines on the CPUs support a lim-

ited number of concurrent threads. Modern quad-core

processors can only run 16 threads in parallel (32 if

the CPUs support Hyper-Threading). By contrast, the

smallest executable unit of parallelism on a device,

called a warp, comprises 32 threads. All NVIDIA

GPUs can support at least 768 active threads per mul-

tiprocessor. On devices that have 30 multiprocessors

(such as the GTX 280), more than 30,000 threads

can run simultaneously (NVIDIA, 2009a). Thus to

take full advantage of the GPU parallel processing ca-

pabilities a large number of threads is required and

that cannot be accomplished using the online training

mode (for the vast majority of the problems).

Table 4 shows how many times the NN weights

are corrected per minute on a GTX 280. The ratio of

the number of weights corrections in the batch mode

relatively to the online mode is far greater on the GPU

than on the CPU, where it represents a small fraction.

This is better emphasized by Table 5 which shows

the ratios between the batch and the online training

modes, for both (i) the number of epochs per minute

and (ii) the number of network weights corrections

per minute. Thus on the GPU, the online training

is not granted to converge faster than the batch train-

ing mode, even in situations where that holds true on

the CPU. In fact, in our experimental tests, we found

the batch training mode to converge faster than all the

other modes for the “two-spirals” and “sonar” bench-

marks. However, in the “Friedman” benchmark, the

mini-batch mode outperformed the batch mode, re-

gardless of the number of selected patterns, which in

turn outperformed the stochastic version. Figure 2

shows the RMS error versus the training mode. Al-

though, we run the mini-batch with 32, 64, 128, 256

and 512 patterns

the graphic only shows two results

(namely, 64 and 512 patterns) for clarity purposes.

The values for the CPU are not presented, but they can

easily be calculated from the data contained in Table 2.

The values selected for the number of patterns in the

mini-batch mode are multiples of the warp size (32) for per-

formance reasons.

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

274

Table 2: Number of epochs trained per minute using the MBP algorithm.

Core 2 6600 8600 GT GTX 280

Benchmark N

online batch online batch online batch

Sonar 104

60 10 – 1 6843.1 7201.7 7471.2 59308.5 11473.9 381079.4

60 20 – 1 3614.0 3894.3 5157.4 29919.5 11145.8 195182.3

60 30 – 1 2527.7 2645.3 3823.4 20163.3 11119.9 148379.0

Two Spirals 194

2 20 10 1 6527.4 7554.1 3531.6 79937.7 4490.5 335420.4

2 30 10 1 4715.4 5280.8 3442.5 56782.7 4293.5 293255.1

2 40 10 1 3486.3 4035.0 2982.9 37990.6 4189.7 237182.3

Friedman 40768

10 20 10 1 17.2 24.8 17.1 347.0 19.8 2089.2

10 30 10 1 11.9 17.2 14.5 249.9 19.0 1675.7

10 40 10 1 9.2 13.2 12.6 138.0 18.3 1279.5

Table 3: GPU speedups over the CPU for the MBP algorithm.

8600 GT GTX 280

Benchmark Patterns N

online batch online batch

Sonar 104

60 10 – 1 1.09 8.24 1.68 52.91

60 20 – 1 1.43 7.68 3.08 50.12

60 30 – 1 1.51 7.62 4.40 56.09

Two Spirals 194

2 20 10 1 0.54 10.58 0.69 44.40

2 30 10 1 0.73 10.75 0.91 55.53

2 40 10 1 0.86 9.42 1.20 58.78

Friedman 40768

10 20 10 1 0.99 13.97 1.15 84.08

10 30 10 1 1.22 14.53 1.59 97.45

10 40 10 1 1.37 10.42 1.99 96.60

Even for large data sets, the online training is not a vi-

able alternative with respect to the batch GPU-based

training mode, because it cannot efﬁciently take ad-

vantage of its inherent parallel processing capabili-

ties. When running the NNs with large datasets a fea-

sible choice to the batch mode can be found on mini-

batch mode. Thus the only valid reason for using the

online mode is memory constraints, since this is the

mode which requires less memory.

Figure 2: Evolution of RMS error accordingly to the train-

ing mode for the “Friedman” benchmark (N

= 30).

6 CONCLUSIONS

In this paper we presented a GPU implementation of

the online (stochastic) training mode of the Multiple

Back-Propagation algorithm. For complex problems

(with sufﬁcient large number of connections) the GPU

online version is faster than the corresponding CPU

version. Nevertheless, our tests showed that the batch

GPU-based training mode is always preferable to the

online training (independently of using a GPU or a

CPU), even for large datasets. However, when train-

ing the neural networks using large datasets the GPU

mini-batch mode represents a wiser choice than the

batch and the online training modes.

The GPU is ideally suited for computations that

can be run in parallel which typically involves thou-

sands, if not millions, arithmetic operations on large

datasets. Neural networks which are highly parallel

learning machines are good examples of the advan-

tage of being programmed in GPU.

Future work will address the GPU-based imple-

mentation of recurrent neural networks.

STOCHASTIC GPU-BASED MULTITHREAD IMPLEMENTATION OF MULTIPLE BACK-PROPAGATION

275

Table 4: Number of times the NN weights are corrected per minute, using a GTX 280.

mini-batch

Benchmark N

online batch N

= 32 N

= 64 N

= 128 N

= 256 N

= 512

Sonar

10 1193287.8 381079.4 581639.6 414031.1 – – –

20 1159161.8 195182.2 349966.5 244664.9 – – –

30 1156465.7 148378.9 286450.9 189953.6 – – –

Two Spirals

20 871164.0 335420.4 615589.1 501868.1 345947.6 – –

30 832947.7 293255.1 564835.0 448190.4 312088.2 – –

40 812805.6 237182.3 507663.2 399210.5 266595.6 – –

Friedman

20 806414.2 2089.2 506097.8 390957.4 256279.8 150710.4 81876.3

30 773508.1 1675.7 433436.5 309343.4 202831.6 118571.7 63747.8

40 746486.7 1279.5 375362.8 257192.4 164875.6 91971.6 48687.8

Table 5: Ratios between the batch and the online training modes, for the number of epochs per minute and for the number of

network weights corrections per minute.

Core 2 6600 8600 GT GTX 280

Benchmark N

epochs corrections epochs corrections epochs corrections

Sonar

10 1.05 0.0101194 7.94 0,0763292 33.21 0,3193525

20 1.08 0.0103610 5.80 0,0557812 17.51 0,1683822

30 1.05 0.0100628 5.27 0,0507083 13.34 0,1283038

Two Spirals

20 1.16 0.0059654 22.63 0,1166737 74.69 0,3850255

30 1.12 0.0057727 16.49 0,0850235 68.30 0,3520691

40 1.16 0.0059659 12.74 0,0656492 56.61 0,2918069

Friedman

20 1.44 0.0000354 20.26 0,0004970 105.62 0,0025907

30 1.44 0.0000354 17.20 0,0004219 88.32 0,0021663

40 1.44 0.0000353 12.22 0,0002997 69.88 0,0017141

REFERENCES

Almeida, L. B. (1997). Handbook of Neural Computation,

chapter C1.2 Multilayer perceptrons, pages C1.2:1–

C1.2:30. IOP Publishing Ltd and Oxford University

Press.

Catanzaro, B., Sundaram, N., and Keutzer, K. (2008). Fast

support vector machine training and classiﬁcation on

graphics processors. In Proceedings of the 25th In-

ternational Conference on Machine Learning (ICML

2008), pages 104–111, Helsinki, Finland.

Che, S., Boyer, M., Meng, J., Tarjan, D., Sheaffer, J. W.,

and Skadron, K. (2008). A performance study of

general-purpose applications on graphics processors

using CUDA. Journal of Parallel and Distributed

Computing, 68(10):1370–1380.

Fahlman, S. E. and Lebiere, C. (1990). The cascade-

correlation learning architecture. In Advances in Neu-

ral Information Processing Systems 2, pages 524–532.

Morgan Kaufmann.

Friedman, J. H. (1991). Multivariate adaptive regression

splines. The Annals of Statistics, 19(1):1–67.

Jang, H., Park, A., and Jung, K. (2008). Neural network im-

plementation using CUDA and OpenMP. In DICTA

’08: Proceedings of the 2008 Digital Image Com-

puting: Techniques and Applications, pages 155–161,

Washington, DC, USA. IEEE Computer Society.

Lopes, N. and Ribeiro, B. (2001). Hybrid learning in a

multi-neural network architecture. Neural Networks,

2001. Proceedings. IJCNN ’01. International Joint

Conference on Neural Networks, 4:2788–2793.

Lopes, N. and Ribeiro, B. (2003). An efﬁcient gradient-

based learning algorithm applied to neural networks

with selective actuation neurons. Neural, Parallel &

Scientiﬁc Computations, 11(3):253–272.

Lopes, N. and Ribeiro, B. (2009). GPU implementation of

the multiple back-propagation algorithm. In Proceed-

ings of Intelligent Data Engineering and Automated

Learning, volume 5788 of Lecture Notes in Computer

Science, pages 449–456. Springer.

NVIDIA (2009a). NVIDIA CUDA C Programming Best

Practices Guide – CUDA Toolkit 2.3.

NVIDIA (2009b). NVIDIA CUDA Programming Guide

Version 2.3.

Schaa, D. and Kaeli, D. (2009). Exploring the multiple-

GPU design space. In Parallel & Distributed Process-

ing, 2009. IPDPS 2009. IEEE International Sympo-

sium on, pages 1–12.

Steinkrau, D., Simard, P. Y., and Buck, I. (2005). Using

GPUs for machine learning algorithms. In ICDAR

’05: Proceedings of the Eighth International Confer-

ence on Document Analysis and Recognition, pages

1115–1119, Washington, DC, USA. IEEE Computer

Society.

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

276