
PROTEINS POCKETS ANALYSIS AND DESCRIPTION
Virginio Cantoni, Riccardo Gatti and Luca Lombardi
University of Pavia, Dept. of Computer Engineering and System Science, Via Ferrata 1, Pavia, Italy
Keywords:
Protein-ligand docking, Curvature analysis, Concavity tree, Travel depth, Pocket mouth area and perimeter.
Abstract:
The development of computational techniques to guide the experimental processes is an important step for the
determination of the protein functions.
The purpose of the activity here described is the characterization of the active sites in protein surfaces and their
quantitative representation. A few pocket parameters like volume, travel depth, mouth area and perimeter,
amplitude parameters, interfacial area ratio, summit density and mean summit curvature are hierarchically
accessible through a concavity tree that topologically represents the entire protein molecule.
This structural representation is particularly useful for the evaluation of binding pockets, the comparison of
the morphological similarity and the identification of potential ligand docking.
1 INTRODUCTION
When a novel experimentally determined protein is
discovered, bioinformatics tools are used to screen
the datasets of proteins with known functionalities,
searching for candidate binding sites for the 3D struc-
ture of the new protein. Specifically, if a region in
the surface of the novel protein has similarities to the
binding site of a known protein the interactions of the
latter are expected candidates in order to discover the
unknown functionalities of the former protein.
The analysis of the binding sites of proteins and
their detection, have been developed on the basis of
different protein representations and matching strate-
gies.
CAST (Liang et al., 1998) and CASTp
(Binkowski et al., 2003) automatically locate
and compute pockets volume and mouth opening area
and circumference of pockets. The algorithm applies
3D computational geometry: a triangulation of the
protein’s surface atoms (which covers a conglomerate
of 3D tetrahedra) is analyzed through convex hull,
alpha shapes and discrete flow theory. A tetrahedron
having at least a triangle that cross the void region is
designated as ’empty tetrahedraon’. Empty tetrahedra
sharing a common triangle are grouped so ’flowing’
towards neighboring larger tetrahedra which act as
sink. A pocket, which is a potential binding site, is
then obtained as collection of empty tetrahedra.
PASS (Brady and Stouten, 2000) is a purely ge-
ometrical method composed of several steps. First,
the protein surface is completely covered by probe
spheres. Second, each probe is associated with a
“burial” value, which corresponds to the number of
atoms contained within a sphere of radius 8
˚
A. Third,
the probes with a “burial” value lower than a prede-
fined threshold are eliminated. Four, these three steps
are iterated (with step one applied only to the parts of
the surface covered by the probes) until no new buried
probe are added. Fifth, a probe weight, which is de-
pendent to the number of their neighboring spheres
and the extent to which they are buried, is assigned.
Finally, a shortlist of active site points (ASPs), ranked
by the probe weight, is selected by identifying the
central probes in regions that contain many spheres
with high burial count. These ASPs represent the loci
of potential binding sites.
In POCKET (Levitt and Banaszak, 1992), the pro-
tein is mapped onto a 3D grid in which a grid point be-
longs to the protein molecule if it is within 3
˚
Afrom
an atom coordinate. The pockets are characterized as
a set of grid points, not belonging to the protein for
which a scanning along the x, y, or z-axes presents a
protein-solvent area-protein sequence (called protein-
solvent- protein event).
LIGSITE (Huang and Schroeder, 2006) extends
POCKET by scanning also along the four cubic diag-
onals in addition to the coordinates axis (in fact, the
previous pocket’s definition produces classifications
that change with the angle between the reference sys-
tem and the protein). The grid points that present a
211
Cantoni V., Gatti R. and Lombardi L. (2010).
PROTEINS POCKETS ANALYSIS AND DESCRIPTION.
In Proceedings of the First International Conference on Bioinformatics, pages 211-216
DOI: 10.5220/0002725302110216
Copyright
c
SciTePress

number of protein-solvent-protein events greater than
a threshold are candidate active sites.
SURFNET-ConSurf (Glaser et al., 2006), rep-
resents the pocket surface by combining geometri-
cal features together with an evolutionary charac-
teristics based on the degree of conservation of the
amino acids involved. SURFNET-ConSurf is based
on a two-stage process. In the former stage, through
SURFNET (Laskowski, 1995) the potential binding
sites in the protein surface are identified. The clefts
are detected by placing a sphere between all pairs of
atoms such that the sphere just touches each atom,
then this sphere is progressively reduced in size up to
no further intersection with other atoms are present.
The resulting sphere is retained only if its radius is
greater than a minimum size predefined. Once the
clefts have been filled by spheres they can be indi-
vidually described by geometric features (e.g. the
volume). In the latter stage, the regions of the re-
sulting clefts that are distant from highly conserved
residues, as defined by the ConSurf-HSSP database
(Glaser et al., 2005), are removed, thus reshaping
the cleft volumes. The second stage is based on
two parameters: the maximum allowed distance and
the minimum conservation score cutoff. The remain-
ing clefts are candidate active sites (in particular the
largest ones).
In this paper we just introduce a feature vector and
describe in details a data structure in order to rep-
resent the pocked extracted by the various methods
to improve the analysis and to reach the needed per-
formance quality. The paper is organized as follows:
in section two a short survey of features for pockets
characterization is given; in section three a data struc-
ture to describe the protein’s pockets, based on a con-
cavity tree representation, which allows the complete
description, at different scales and abstraction levels,
supporting at each level the feature vector description
previously introduced, is presented. In section four a
practical case is described. The last section five con-
tains the conclusion and the near future subsequent
activity.
2 FEATURES FOR POCKET
DESCRIPTION
The goal of this paper is the characterization of each
pocket, which is extracted by segmenting the protein
surface, through morphological and topological quan-
titative descriptors. These features are enriched with
local biochemical features (types of residues and their
characteristics) to detect and specialize the active sites
of a protein.
We are considering now a second step of the pro-
cess of active sites identification, that is, we start
knowing the segmentation of the protein surface in a
number of pockets and tunnels. In particular, we will
refer to the method given in (Cantoni et al., 2009c) but
the technique described in the sequel is not limited to
this particular solution.
2.1 Preliminary Statements
In the discrete space the protein is defined in a 3D
grid (CG) of dimension L x M x N voxels. Note
that the grid is extended one voxel beyond the min-
imum and maximum coordinate of the SES (Solvent-
Excluded Surface, also known as the molecular sur-
face or Connolly surface, generated by the envelope
of a rolling sphere over the van der Waals atoms sur-
face
1
) in each orthogonal direction, in this way both
SES and Convex Hull (CH) borders are inside the CG
border. The voxel resolution adopted is 0.25
˚
A, so as
to be small enough to ensure that, with the used radii
in biomolecules atoms
2
, any concave depression or
convex protrusion is represented by at least one voxel.
The CH of a molecule is the smallest convex poly-
hedron that contains the molecule points. In R
3
the
CH is constituted by a set of facets, that are trian-
gles, and a set of ridges (boundary elements) that
are edges. A practical O(n log n) algorithm for gen-
eral dimensions CH computing, is Quickhull (Barber
and Dobkin, 1996), that uses less space and executes
faster than most of the others algorithms. Let us call
R the region between the CH and the SES (the con-
cavity volume (Borgefors and Sanniti Di Baja, 1996)),
that is:
R = CH ∩ SES (1)
and Re the connected component of R adjacent to the
CH border; that is Re and R differ for the cavities
C: the volumes completely enclosed in the macro-
molecule M:
C = CH − Re − M (2)
The region Re has been partitioned into a set of dis-
joint segments P
SES
= {P
1
, . . . , P
j
, . . . , P
N
}, where N
is the number of pockets and tunnels. The partition
must satisfy the following condition:
P
i
∩ P
j
= ∅, i 6= j (3)
P
1
∪ · · · ∪ P
j
∪ · · · ∪ P
n
= R
e
(4)
1
The radius of the solvent sphere is usally set to the ap-
proximate radius of a water molecule.
2
The smallest used atom is oxygen having a Van der
Walls radius of 1.4
˚
A
BIOINFORMATICS 2010 - International Conference on Bioinformatics
212

Our goal is to define a feature vector to represent, in
a discriminant way to facilitate processing and statis-
tical analysis, each pocket of P
SES
. Many vector’s pa-
rameters need a reference plane that we have identi-
fied with the one to which it belongs the largest CH’s
triangle involved in the pocket.
2.2 Basic Features
The problem of defining an optimal set for feature
selection is complicated because, besides building
robust models, it is also important simplifying the
amount of resources required to describe the data
accurately, without ambiguity, in a very large set
of redundant and relevant information. The expert
can help, but can usually construct only a set of
application-dependent features.
An extended set of general features that can be,
in peculiar cases, partitioned in well-organized pro-
ficient subsets, is the following: i) Pocket Volume
(Laskowski et al., 1996), ii) Surface to Volume Ra-
tio, iii) Skewness and Kurtosis of Height Distribu-
tion (Blunt and Jiang, 2003), iv) Mouth Aperture (in
details we consider area, perimeter and the perime-
ter to area ratio), v) Travel Depth (Coleman and
Sharp, 2006) (Giard et al., 2008), vi) Top Peaks and
Valleys, vii) Summit Density, Mean Summit Curva-
tures (both the average of the principal curvatures of
peaks and valleys (Coleman et al., 2005), (Cantoni
et al., 2009a)), viii) Interfacial Area Ratio, and ix)
Residue Conservation (Glaser et al., 2006) (the con-
servation score for each residue in a given protein can
be obtained from the ConSurf-HSSP database (Glaser
et al., 2005)).
3 THE DATA STRUCTURE
One of the most successful approaches for shape anal-
ysis and description is the structural one. We think
that this is particularly fruitful in proteomics in which
the morphology plays a fundamental role. A complex
shape, like the Re, is segmented into its component
(the pockets set), and each pocket can be subsequently
decomposed into simpler region, and the complete de-
scription is given in terms of the region’s features and
their spatial relationship. Nevertheless, pocket shapes
can be rather complex and not directly decomposable
into simpler regions. However we can re-apply the
segmentation process of the Re into the pockets. This
process can be executed recursively. In this way a se-
quence of approximations is built, and, at each stage,
exact measures of the remaining concavities, based on
the parameters described above, are given. This struc-
tural hierarchical description and analysis, guided by
the concavities (Borgefors and Sanniti Di Baja, 1992),
seems to us a very promising effective description.
The basic structure of the approach was firstly in-
troduced in (Arcelli and Sanniti Di Baja, 1978) and in
(Borgefors and Sanniti Di Baja, 1996) has been finally
called concavity tree: “components of C (Re in our
3D case) for which the internal section of the perime-
ter (surface in 3D) exceeds the external section are
structured concavities. A more sophisticated anal-
ysis of these regions is performed to extract further
features. The envelopes CH of the concavity regions
are computed using the same process as that applied
to the original pattern. Merging can occur while fill-
ing meta-concavities, so the concavity regions must
be labeled and processed individually. For each con-
cavity region, its meta-concavities are identified. The
process continues until all regions are convex”.
The final result is a hierarchical structure, the
(meta) concavity tree. At each level the concavities
can be analyzed and described on the basis of the
above feature vector - computed at each node: ob-
viously the features defined for concavities can also
be computed for the meta-concavities.
The “concavities” (three “pockets” and one “tun-
nel”) and four second level meta-concavities of a 2D
example are shown in Figure 1. Figure 2 shows con-
cavities and meta-concavities of level two, three and
fourth for the tunnel of level one. The corresponding
concavity tree is shown in Figure 3. Note that termi-
nating nodes, i.e. regions without significant concav-
ities, are highlight with a bordeaux contour.
Figure 1: A 2D representation example with a tunnel and
three pockets in a section composed of three connected
components (in brown). The closed curve in black corre-
sponds to the first level convex hull, and the border in brown
dotted-dashed line embodies the area under analysis. Part
of the second level with three meta-concavities (A, B, C)
is shown; in evidence also five third level termination-node
components (A1, A2, C1, D1, and D2).
PROTEINS POCKETS ANALYSIS AND DESCRIPTION
213
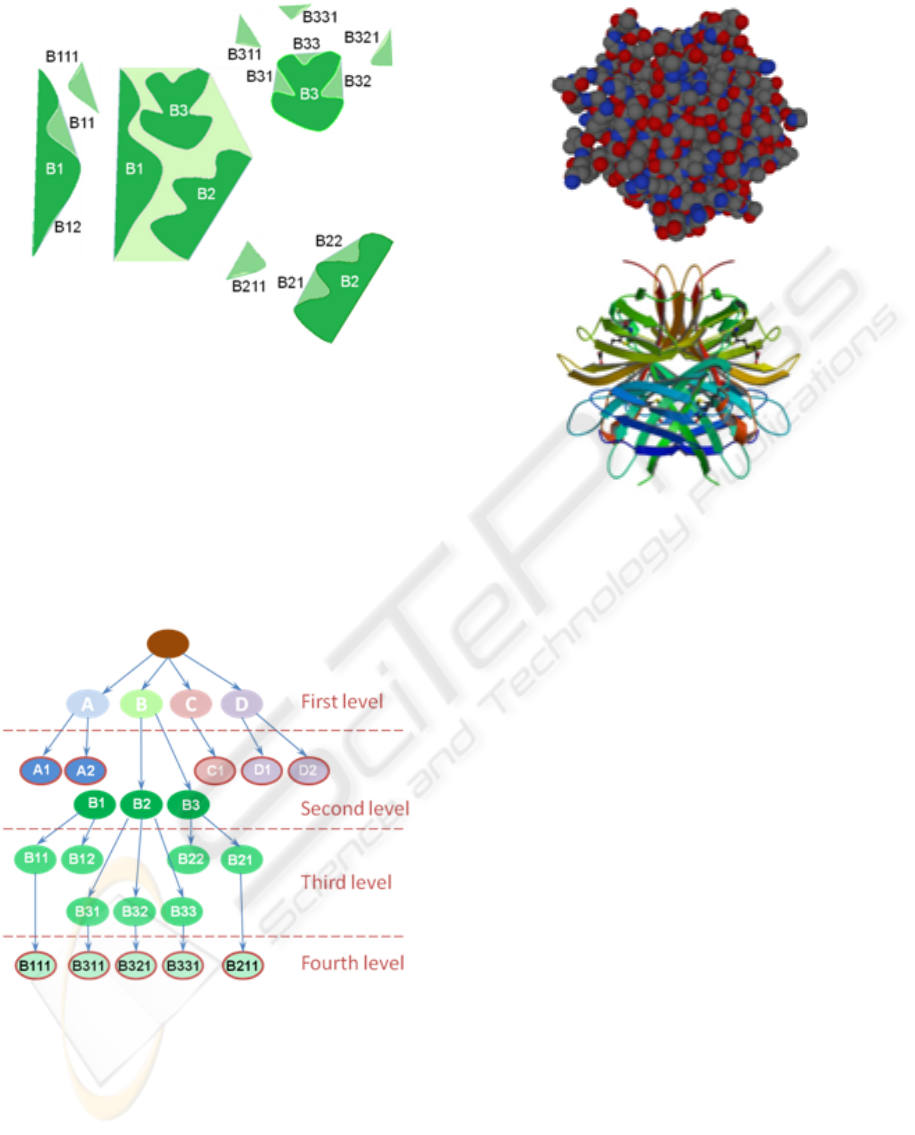
Figure 2: Continuing the 2D representation example of Fig-
ure 1, the details of the tunnel B component (light green)
are shown. The second level is composed of the three meta-
concavities (B1, B2, and B3). Each one has concavities at
the third level: B1 has a termination-node concavity (B12)
and a second component B11 which maintains a meta con-
cavity at the fourth level B111; B2 has a termination-node
concavity (B22) and a second component B21 which main-
tains a meta concavity at the fourth level B211; finally, B3
has three node concavities (B31, B32, B33) each one main-
taining a meta-concavity node-component B311, B321 and
B331 respectively, at the fourth level.
Figure 3: Representation of the concavity tree for the 2D
section of Figures 1 and 2. Note that each node contains the
information of the feature vector previously presented.
4 EXAMPLE OF A PRACTICAL
REPRESENTATION
A practical example of our hierarchical representa-
tion is given in figure 4 referring to the Apostrepta-
Figure 4: On the top the ’space filling’ representation of
1MK5. The colours follow the standard CPK scheme. On
the bottom the correspondent secondary structure represen-
tation.
vidin Wildtype Core-Streptavidin with Biotin struc-
ture (1MK5 in PDB).
As mentioned above, the analysis is accomplished
with a resolution of 0.25
˚
A, which entails a van der
Waals radius of more than five voxels to the small-
est represented atoms. The representation is related
to the SES obtained from the quoted surface, after the
execution of a closure operator, using a sphere with
radius of 1.4
˚
A, approximately 6 voxels, (correspond-
ing to the conventional size of a water molecule) as
structural element (see figure 5).
The segmentation of concavities and meta-
concavities is computed with the technique given in
(Cantoni et al., 2009b), where the two parameters that
characterize the execution, the minimum passage sec-
tion θ
1
and the maximum mouth aperture θ
2
have
been fixed to 200 voxels (which for a circle corre-
sponds to a radius of about 8 voxels) and 2000 voxels
(which for a circle corresponds to a radius of about 25
voxels).
Figure 6 represents the complete concavity tree for
the 4 main pockets and tunnels.The molecule is rep-
resented inside its own convex hull which is drawn
completely on the backside and only through its edges
in the front side.
This process is conducted on the basis of other
two thresholds: θ
3
represents the minimum concav-
BIOINFORMATICS 2010 - International Conference on Bioinformatics
214

Figure 5: Solvent Excluded Surface of 1MK5 achieved
from the van der Waals surface with a sequence of dilation-
erosion operators.
Figure 6: First level of the concavity tree of the Apostrepta-
vidin Wildtype Core-Streptavidin with Biotin structure. The
representation is limited to the first five tunnels or pockets,
ranked on the basis of the travel depth.
ity travel depth and θ
4
represents the minimum open
mouth at the distance θ
3
. These two parameters, in
the current execution, has been set to 2 voxels and 4
voxels respectively.
Figure 7 presents the sub-tree corresponding to the
largest tunnel/pocket. Following the hierarchical rep-
resentation, the volume of the components, descend-
ing the tree are more and more reduced (in fact, this
path corresponds to a multiscale process).
Note that, each node is described quantitatively
through the geometrical, topological and biochemical
parameters of the features vector described above. Fi-
nally, it is worth to point out that, as it has been shown
in (Laskowski et al., 1996) for the enzymes, the active
site is commonly found in the largest cleft.
5 CONCLUSIONS
As morphology is important for protein recognition
and function, the development of shape representa-
Figure 7: Complete hierarchical representation of the sub-
tree of the main pocket of the 1MK5, spanning six levels.
tion and analysis techniques is important in structure-
based drug development and design.
The identification and the representation of pro-
tein cavities is a basic step for the study of sites of
activity in proteins. In this paper we presented a gen-
eral framework to evaluate geometric and topologic
parameters to represent size and form of the pock-
ets and biochemical feature, in a hierarchical multi-
level data-structure. This description is suited for the
implementation of automatic procedures for the anal-
ysis, the prediction and the comparison of potential
binding sites.
What is important now is to proceed to a statisti-
PROTEINS POCKETS ANALYSIS AND DESCRIPTION
215

Figure 8: Complete concavity tree of the five main pockets
of the 1MK5.
cal selection of a subset of relevant features for build-
ing robust models. The exclusion of redundant fea-
tures, by reducing the dimension of the parameter
space, improves the time performance and facilitates
fast searching, processing and statistical analysis.
REFERENCES
Arcelli, C. and Sanniti Di Baja, G. (1978). Polygonal cov-
ering and concavity tree of binary digital pictures. In
Proceeding International Conference MECO 78, page
292297.
Barber, C. B. and Dobkin, D. P. (1996). The quickhull algo-
rithm for convex hulls. ACM Transactions on Mathe-
matical Software, 22:469–483.
Binkowski, A. T., Naghibzadeh, S., and Liang, J. (2003).
Castp: Computed atlas of surface topography of pro-
teins. Nucl. Acids Res., 31(13):3352–3355.
Blunt, L. and Jiang, X. (2003). Advanced Techniques for As-
sessment Surface Topography (1st edn.). Penton Press,
London.
Borgefors, G. and Sanniti Di Baja, G. (1992). Methods for
hierarchical analysis of concavities. In Proceedings of
the Conference on Pattern Recognition (ICPR), vol-
ume 3, pages 171–175.
Borgefors, G. and Sanniti Di Baja, G. (1996). Analyzing
non convex 2d and 3d patterns. Computer Vision and
Image Understanding, 63(1):145–157.
Brady, G. P. and Stouten, P. F. (2000). Fast prediction and
visualization of protein binding pockets with pass. J
Comput Aided Mol Des, 14(4):383–401.
Cantoni, V., Gatti, R., and Lombardi, L. (2009a). Ap-
proaches for protein surface curvature analysis. In
ICIAP 2009, in press.
Cantoni, V., Gatti, R., and Lombardi, L. (2009b). Proteins
pockets quantitative description. In DIS-UNIPV inter-
nal report.
Cantoni, V., Gatti, R., and Lombardi, L. (2009c). Segmen-
tation of ses for protein structure analysis. In BIOIN-
FORMATICS 2010, submitted to.
Coleman, R. G., Burr, M. A., Souvaine, D. L., and Cheng,
A. C. (2005). An intuitive approach to measuring pro-
tein surface curvature. Proteins, 61(4):1068–1074.
Coleman, R. G. and Sharp, K. A. (2006). Travel depth, a
new shape descriptor for macromolecules: application
to ligand binding. J Mol Biol, 362(3):441–458.
Giard, J., Patrice, R. A., and Macq, B. (2008). Fast and
accurate travel depth estimation for protein active site
prediction. SPIE Electronic Imaging, San Jose 2008,
pages 0Q–10Q.
Glaser, F., Morris, R. J., Najmanovich, R. J., Laskowski,
R. A., and Thornton, J. M. (2006). A method for lo-
calizing ligand binding pockets in protein structures.
Proteins, 62(2):479–488.
Glaser, F., Rosenberg, Y., Kessel, A., Pupko, T., and Ben-
Tal, N. (2005). The consurf-hssp database: the map-
ping of evolutionary conservation among homologs
onto pdb structures. Proteins, 58(3):610–617.
Huang, B. and Schroeder, M. (2006). Ligsitecsc: predict-
ing ligand binding sites using the connolly surface
and degree of conservation. BMC Structural Biology,
6(1):19+.
Laskowski, R. A. (1995). Surfnet: a program for visual-
izing molecular surfaces, cavities, and intermolecular
interactions. J Mol Graph, 13(5).
Laskowski, R. A., Luscombe, N. M., Swindells, M. B., and
Thornton, J. M. (1996). Protein clefts in molecular
recognition and function. Protein Sci, 5(12):2438–
2452.
Levitt, D. G. and Banaszak, L. J. (1992). Pocket: a com-
puter graphics method for identifying and displaying
protein cavities and their surrounding amino acids. J
Mol Graph, 10(4):229–234.
Liang, J., Edelsbrunner, H., and Woodward, C. (1998).
Anatomy of protein pockets and cavities: measure-
ment of binding site geometry and implications for
ligand design. Protein Sci, 7(9):1884–1897.
BIOINFORMATICS 2010 - International Conference on Bioinformatics
216
