A TOOL ENVIRONMENT FOR SPECIFYING AND VERIFYING

MULTI-AGENT SYSTEMS

Christian Schwarz, Ammar Mohammed

Universit¨at Koblenz-Landau, Computer Science Department, 56070 Koblenz, Germany

Frieder Stolzenburg

Hochschule Harz, Automation and Computer Sciences Department, 38855 Wernigerode, Germany

Keywords:

Multi-agents speciﬁcation, Veriﬁcation, Hybrid automata.

Abstract:

We present a tool environment with a constraint logic programming core, that allows us to specify multi-agent

systems graphically and verify them automatically. This combines the advantages of graphical notations from

software engineering and formal methods. We demonstrate this on a Robocup rescue scenario.

1 INTRODUCTION

Specifying the behavior of multi-agent systems

(MAS) in safety critical environments is a demand-

ing task. Henzinger (1996) introduced Hybrid Au-

tomata (HA) which have been used to model and

verify MAS, especially because of their capability

to catch both, the continuous dynamics of physical

systems and the discrete evolution of computational

systems. Mohammed and Stolzenburg (2008, 2009)

mention several of application areas and benchmarks.

With the help of veriﬁcation tools like HyTech (Hen-

zinger et al., 1995) and PHAVer (Frehse, 2005) one

can verify and control multi-agent plans. But the spec-

iﬁcation and veriﬁcation of MAS behaviors by means

of hybrid automata is still a challenging task.

One of the problems, which is especially difﬁcult

for MAS, is that the state space grows exponentially

in the number of states in the composed automata.

Mohammed and Stolzenburg (2008) have presented

an approach based on constraint logic programming

(CLP) which tackles this problem. However, so far

a graphical user-interface for the deﬁnition of MAS

has not been available. Therefore, this paper aims at

the simpliﬁcation of the speciﬁcation process by tak-

ing advantage of the graphical notations taken from

software engineering more directly. Mohammed and

Schwarz (2009) presented a prototype, that allows to

enter the model of a hybrid automaton and its re-

quirements graphically and which automates the ver-

iﬁcation process. Here, we present an extension of

this tool and demonstrate it in a scenario from the

RoboCup rescue scenario.

2 HYBRID AUTOMATA

We describe MAS by means of several hybrid au-

tomata, where a single agent is represented by one au-

tomaton. This section brieﬂy into their the syntax and

semantics. A hybrid automaton is represented graph-

ically as a state transition diagram like statecharts in

the uniﬁed modeling language (UML) Object Man-

agement Group, Inc. (2009), augmented with mathe-

matical annotations on transitions and locations. For-

mally speaking, a hybrid automaton, which represents

an agent in a continuous domain, is deﬁned as fol-

lows:

Deﬁnition 1: A hybrid automaton is a tuple H =

(X, Q, Inv, Flow, E, Jump, Reset, Event,

) where:

• X is a set of real variables that describe the con-

tinuous dynamics of the automaton.

• Q is a ﬁnite set of control locations.

• Inv(q) is the invariant predicate, which assigns a

constraint on the valuation to each location.

• Flow(q) is the ﬂow predicate on the valuation for

each location. In the graphical representation, a

ﬂow of a variable x is denoted as ˙x.

323

Schwarz C., Mohammed A. and Stolzenburg F. (2010).

A TOOL ENVIRONMENT FOR SPECIFYING AND VERIFYING MULTI-AGENT SYSTEMS.

In Proceedings of the 2nd International Conference on Agents and Artiﬁcial Intelligence - Agents, pages 323-326

DOI: 10.5220/0002727703230326

 SciTePress

• E ⊆ Q× Q is the discrete transition relation over

the control locations. Each edge may have the fol-

lowing annotations:

Jump denotes a jump condition (guard), which is

a constraint over the variables that must hold

to ﬁre transitions. Omitting a jump condition

means, that it is true.

Reset is a constraint, which may reset the vari-

ables by executing a speciﬁc assignments. In

the graphical representation, x

′

= v denotes that

the variable x is reset to the value v. Omitting

Reset means, that the variablesare not changed.

Event is a synchronization label, used to syn-

chronize and coordinate concurrent automata.

•

∈ Q× R

is the initial state.

The semantics of a hybrid automaton is deﬁned in

terms of a labeled transition system between states,

where a state is deﬁned as follows:

Deﬁnition 2: The state

of a hybrid automaton is

given by

= hq, vi ∈ Q × R

where v = (a

, . . . , v

)

and v

assigns a value to each variable x

∈ X. The

state is admissible iff Inv(q)[v] holds.

A state transition system of a hybrid automaton

H starts with the initial state

. It then evolves de-

pending on two kinds of transitions: continuous tran-

sitions, capturing the continuous evolution of states,

and discrete transitions, capturing the changes of lo-

cation. More formally, we can deﬁne the operational

semantics as follows:

Deﬁnition 3: For each transition between two admis-

sible states

= hq

, v

i and

= hq

, v

i one of the

following condition holds:

(discrete) There is an edge e = (q

, q

) ∈ E,

Jump(e)[v

] holds and the variables are reset ac-

cording to Reset(e). In addition an event a ∈

Event(e) occurs. A discrete transition can be writ-

ten as q

→ q

(continuously) In this case q

= q

holds, ∆t is the

time spent in q

and v

are valuations of

the variables according to Flow(q

) with respect

to ∆t. The invariant predicate Inv(q

) must hold

continuously during ∆t.

The continuous evolution generates an inﬁnite

number of reachable states. Thus the state-space ex-

ploration techniques require an appropriate symbolic

representation for sets of states. We represent the in-

ﬁnite states symbolically as ﬁnite intervals which are

called regions.

Deﬁnition 4: A region Γ = hq,Vi is the set of possible

states reached at location q by means of continuous

transitions, where V represent an interval of reached

valuations of the variables. A region Γ is admissible

if inv(q)[v] holds for all v ∈ V.

Now, the run of hybrid automata can be deﬁned as

a form of reached regions, where the change from one

region to another is induced using a discrete step.

Deﬁnition 5: A run of hybrid automaton H is

∑

, ..., a (possibly inﬁnite) sequence of admissible

regions, where a transition from a region Γ

to a region

i+1

is enabled (written as Γ

→ Γ

i+1

), if q

→ q

i+1

where a ∈ Event is the generated event before the con-

trol goes to the region Γ

i+1

. Γ

is the initial region

reached from a start state

by means of continuous

transitions.

The operational semantics is the basis for veri-

ﬁcation of a hybrid automaton. In particular, model

checking of a hybrid automaton is deﬁned in terms of

the reachability analysis of its underlying transition

system. The most useful question to ask about hybrid

automata is the reachability of a given state. Thus, we

deﬁne the reachability of states as follows.

Deﬁnition 6: A region Γ

is called reachable in

∑

, if

⊆

∑

. Consequently, a state

is called reachable,

if there is a reached region Γ

such that

∈ Γ

To specify MAS, hybrid automata can be com-

posed in parallel, where a hybrid automaton is given

for each agent in the MAS, and communication be-

tween the different agents may occur via shared vari-

ables and synchronization labels. Technically, the par-

allel composition of hybrid automata is obtained from

the different parts using a Cartesian product con-

struction (composition) of the participating automata.

The transitions from the different automata are in-

terleaved, unless they share the same synchroniza-

tion label. In this case, they are synchronized during

the execution. Differently to most of hybrid automata

techniques, Mohammed and Stolzenburg(2008) show

how the composition of hybrid automata can be con-

structed on the ﬂy. Additionally, they presented a CLP

approach to encode the previous semantics.

3 THE RESCUE EXAMPLE

In the RoboCup rescue simulation league (Tadokoro

et al., 2000) a team of heterogeneous agents is simu-

lated in a city which is partly destroyed by an earth-

quake. The agents (e.g. police, ﬁre brigade and am-

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

324

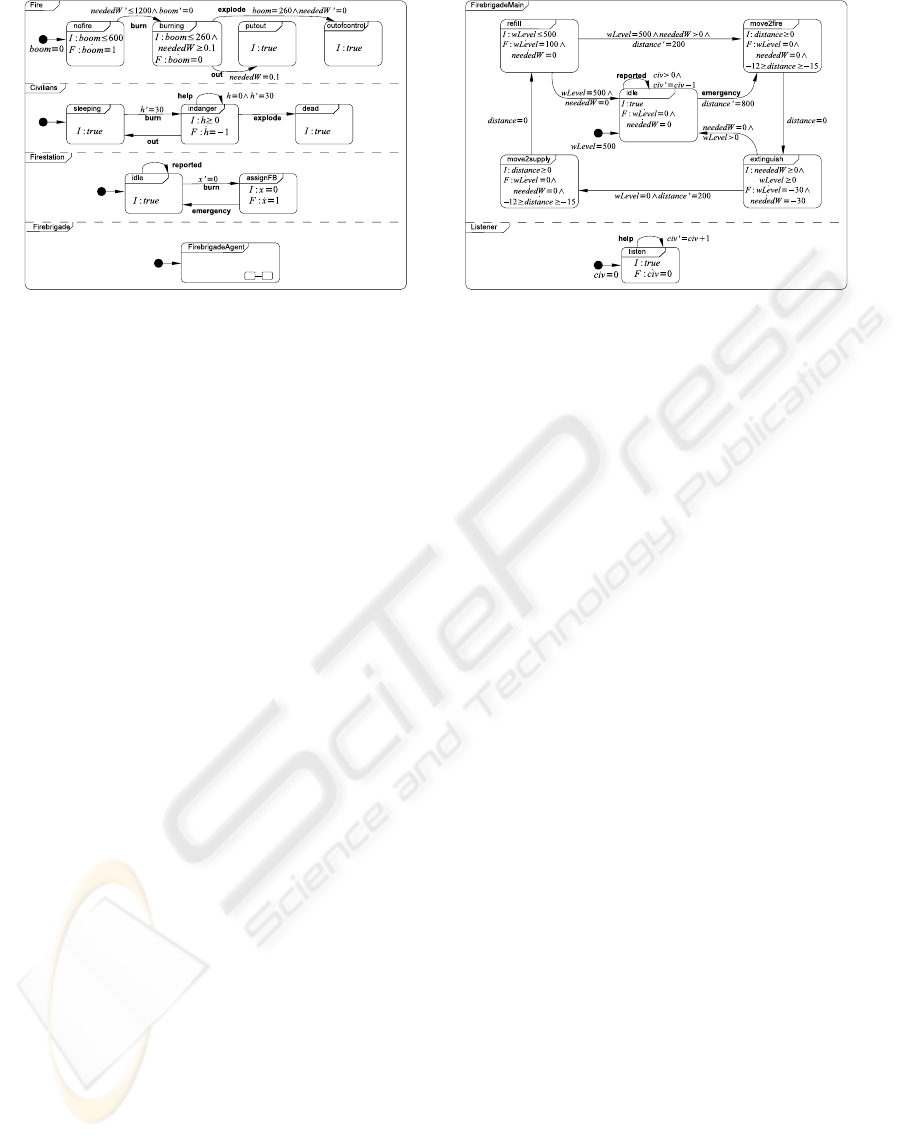
(a) The environment (b) The ﬁre brigade agent

Figure 1: A scenario from the RoboCup rescue simulation league modeled as hybrid automata.

bulance) can solve one speciﬁc task only. So the need

for coordination and synchronization is obvious.

3.1 Speciﬁcation

Consider the following simple scenario. When a ﬁre

breaks out somewhere in the city, a ﬁre brigade agent

is ordered by its headquarters to extinguish the ﬁre.

If the agent runs out of water it has to reﬁll its tank

at a supply station and return to the ﬁre to complete

its task. When the ﬁre is put out, the brigade agent

will become idle again and wait for its next opera-

tion. Additionally the agent has to report any discov-

ered injured civilian. A limiting factor is, that the ﬁre

will eventually get out of control, so it must be extin-

guished within a speciﬁed time limit.

The environment is modeled in Fig. 1(a). The ﬁre

will start within the ﬁrst 10 minutes of the simulation.

The variable neededW represents the amount of water

that is needed to put it off. The civilians are modeled

to be sleeping initially. When the ﬁre breaks out, they

will wake up and call for help periodically. The task

of the ﬁre station is to assign a ﬁre brigade to a ﬁre as

soon as it is discovered.

The ﬁre brigade agent is modeled in Fig. 1(b). It

consists of two parts: the main control structure Fire-

brigadeMain and Listener that counts the number of

discovered civilians. FirebrigadeMain starts in idle

and jumps to move2ﬁre, which models the moving to-

wards the ﬁre, when it is assigned by the ﬁre station.

The distance between ﬁre and the the ﬁre brigade is

modeled by the variable distance.

After it has arrived at the ﬁre, the ﬁre brigade tries

to extinguish it. This is modeled by decreasing the

value of wLevel (the water in the tank) , and neededW

(the water needed to put out the ﬁre) by the same rate.

If the water in the tank runs out, the ﬁre brigade has

to move to the next reﬁll station. After the tank is re-

ﬁlled, the ﬁre brigade moves towards the ﬁre again.

After the ﬁre is put off or is got out of control, the ﬁre

brigade becomes idle again and can then report any

found civilians.

3.2 Veriﬁcation

Using this model, we can now demonstrate some ex-

emplary model checking tasks. We can examine if

certain control locations are reachable. So we can

ask: “Is it possible to extinguish the ﬁre?” ( putout

is reachable), or “Won’t the ﬁre get out of control?”,

(outofcontrol is not reachable). It is also possible, to

check the reachability of composed locations. This al-

lows questions like “Won’t the ﬁre brigade move to

the ﬁre if it is not burning?” Then, no composed loca-

tions are reachable, where Firebrigade is in move2ﬁre

and Fire is in noﬁre, putout or outofcontrol. Further-

more, we can check the reachability of certain in-

tervals in the continuous valuation of the automaton,

e.g.: “Won’t the agent try to extinguish with an empty

water tank?” This would hold if extinguish is active

while wLevel < 0.

Finally, we can check properties of runs. This al-

lows more complex questions like “Does the agent re-

port all discovered civilians?” This question contains

two properties to be checked: (a) all discovered civil-

ians are reported eventually and (b) the agent does

never report a civilian than he did not ﬁnd. Property

(a) corresponds to the fact that from every reachable

state there is a state reachable where all discovered

civilians have been reported. Property (b) holds if in

the history of each reachable state the number of tran-

sitions labeled with help is always greater or equal

than the number of transitions labeled with reported.

A TOOL ENVIRONMENT FOR SPECIFYING AND VERIFYING MULTI-AGENT SYSTEMS

325

Figure 2: A screenshot of HieroMate while verifying the ﬁre

brigade example (some of the automata are hidden).

4 THE HIEROMATE TOOL

Mohammed and Schwarz (2009) initially presented

a tool for graphical speciﬁcation and veriﬁcation of

hierarchical hybrid automata (HHA), that include hi-

erarchical speciﬁcations as known from UML state-

charts, such that the overall system can be expressed

on several levels of abstraction. In HHA, locations are

generalized (cf. Mohammed and Stolzenburg, 2008):

The set of all locations Q is partitioned simple, com-

posite and concurrent locations. In essence, the loca-

tions of plain hybrid automata correspond to simple

locations in HHA.

Now, in this paper, the concurrent view based on

the outline in Mohammed and Stolzenburg (2008) has

also been plugged into the tool, such that a user can

select which type of view is needed to be modeled.

This tool works as a front end for a model checking

engine that is written in the CLP language ECLiPSe

Prolog (Apt and Wallace, 2007). The tool assists the

user in specifying hybrid automata (and MAS) by

supporting graphical speciﬁcation, on-the-ﬂy syntax

checking, and automated CLP code generation.

The user interaction is realized mainly using con-

text sensitive menus that allow only meaningful ac-

tions e.g. the user will be able to add another location

to an automaton by right clicking onto the automa-

ton and selecting the item “Add location” from the

context menu. The speciﬁcation can then be checked

directly in the tool. Therefore the user can either spec-

ify queries manually using CLP Prolog, use the tool

to generate simple queries automatically, or combine

both methods. Fig. 2 shows a screenshot of HieroMate

while verifying the rescue example.

5 CONCLUSIONS

In this paper, we presented a tool environment with

a constraint logic programming core that is able to

graphically specify and formally verify MAS in terms

of hybrid automata, where the graphical speciﬁcation

and a requirement can be given to the tool and it

will convert them into a speciﬁcation written in CLP.

Then, the resulting CLP speciﬁcation will be checked

using an abstract state machine in terms of reacha-

bility analysis automatically. The paper has demon-

strated this on a MAS scenario taken from rescue sce-

nario.

REFERENCES

Apt, K. R. and M. Wallace (2007). Constraint Logic Pro-

gramming Using ECLiPSe. Cambridge, UK: Cambridge

University Press.

Frehse, G. (2005). PHAVer: Algorithmic veriﬁcation of hy-

brid systems past HyTech. In M. Morari and L. Thiele

(Eds.), Hybrid Systems: Computation and Control, 8th

International Workshop, Proceedings, LNCS 3414, pp.

258–273. Springer.

Henzinger, T. (1996). The theory of hybrid automata. In

Proceedings of the 11th Annual Symposium on Logic in

Computer Science, New Brunswick, NJ, pp. 278–292.

IEEE Computer Society Press.

Henzinger, T., P.-H. Ho, and H. Wong-Toi (1995). HyTech:

The Next Generation. In IEEE Real-Time Systems Sym-

posium, pp. 56–65.

Mohammed, A. and C. Schwarz (2009). HieroMate: A

graphical tool for speciﬁcation and veriﬁcation of hier-

archical hybrid automata. In B. Mertsching, M. Hund,

and Z. Aziz (Eds.), KI 2009: Advances in Artiﬁcial In-

telligence, Proceedings of 32nd Annual German Confer-

ence on Artiﬁcial Intelligence, LNAI 5803, Paderborn,

pp. 695–702. Springer, Berlin, Heidelberg, New York.

Mohammed, A. and F. Stolzenburg (2008). Implementing

hierarchical hybrid automata using constraint logic pro-

gramming. In S. Schwarz (Ed.), Proceedings of 22nd

Workshop on (Constraint) Logic Programming, Dres-

den, pp. 60–71. University Halle Wittenberg, Institute of

Computer Science. Technical Report 2008/08.

Mohammed, A. and F. Stolzenburg (2009). Using constraint

logic programming for modeling and verifying hierarchi-

cal hybrid automata. Arbeitsberichte des Fachbereichs

Informatik 6/2009, Universit¨at Koblenz-Landau.

Object Management Group, Inc. (2009). OMG Uniﬁed

Modeling Language (OMG UML): Infrastructure; Su-

perstructure. Object Management Group, Inc.

Tadokoro, S. et al. (2000). The RoboCup-Rescue project:

A robotic approach to the disaster mitigation problem.

In Proceedings of IEEE International Conference on

Robotics and Automation (ICRA 2000), pp. 4089–4104.

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

326