AN AGENT-BASED OPTIMIZATION APPROACH FOR

DISTRIBUTED PROJECT SCHEDULING IN SUPPLY CHAIN

WITH PARTIAL INFORMATION SHARING

Hanlin Zhang

, Guorui Jiang

and Tiyun Huang

1,2

School of Economic and Management, Beijing University of Technology, Beijing, China

School of Management, Harbin Institute of Technology, Harbin, China

Keywords: Agent, Optimization, Project Scheduling, Supply Chain, Negotiation, Heuristic Approach.

Abstract: This paper focuses on the optimization problem of distributed project scheduling in the supply chain

network which is made up of order manager, service brokers and service suppliers. Based on the initial

scheduling by bids of service brokers, we present a heuristic approach with agent negotiation mechanism for

the problem. The approach seeks optimal schedule by distributed negotiations, which apply the agent

negotiation mechanism and share limited information, between order manager and brokers. Computational

experiments show the approach is effective with good optimization performance.

1 INTRODUCTION

With the development of information technology,

individual entities can dynamically form project-

based alliances, such as virtual enterprise, to meet

order demands through effective sharing and

applying of resources (Huang et al., 2005). This

distributed network structure of the supply chain

poses greater challenges on project scheduling, and

the research on scheduling problem in this

environment getting an increasing concern.

There are many research works about project

scheduling in a supply chain and most of them focus

on centralized decision making, such as Banaszak &

Zaremba (2006), Banaszak et al. (2009), Lecompte

et al. (2000), Vairaktarakis & Hosseini (2008).

These research works generally assume that the

supply chain manager could take decisions by

applying a centralized optimization model and could

obtain all the information they need. However, some

of the information is frequently seemed to be private

and won't to share, such as the resource capability

and cost structures.

Then, increasing studies about Distributed

Project Scheduling Problem (DPSP) in supply chain

with incomplete information are emerging. Lau et al.

(2006) presented a model base on agent for DPSP,

and use a modified contract net protocol to share

time window between project agents and contractor

agents and to seek a feasible solution of the

scheduling. Huang et al. (Huang et al., 2005, 2006)

focused on analyzing affected operations

rescheduling when the resource condition is changed.

Wang et al. (2008) introduce argument negotiation

method for scheduling problem of supply chain to

promote negotiation efficiency among broker agents.

These studies formulated distributed supply chain

network with agents, who are intelligent,

independent and autonomic, and coordinated

conflicts caused by resource constraints through

sharing less information to obtain a valid schedule.

However, as the studies focused on solving conflicts,

the global optimization performance of the

scheduling is usually not very good.

As a result, base on a multi-agent architecture,

this paper presents a heuristic which is combined

with agent negotiation mechanism for performing

the optimal project schedule in supply chain with

partial information sharing. The information,

includes new solution and cost changing of the order

manager, and new proposal, concessionary proposal

and relevant cost-time changing of broker, is

considered for sharing. Taking advantage of the

relationship between the new proposals and the

concessionary proposals of the brokers, the order

manager and the brokers could get the optimal

schedule by negotiate each other iteratively.

603

Zhang H., Jiang G. and Huang T. (2010).

AN AGENT-BASED OPTIMIZATION APPROACH FOR DISTRIBUTED PROJECT SCHEDULING IN SUPPLY CHAIN WITH PARTIAL INFORMATION

SHARING.

In Proceedings of the 2nd International Conference on Agents and Artiﬁcial Intelligence - Artiﬁcial Intelligence, pages 603-606

DOI: 10.5220/0002727806030606

 SciTePress

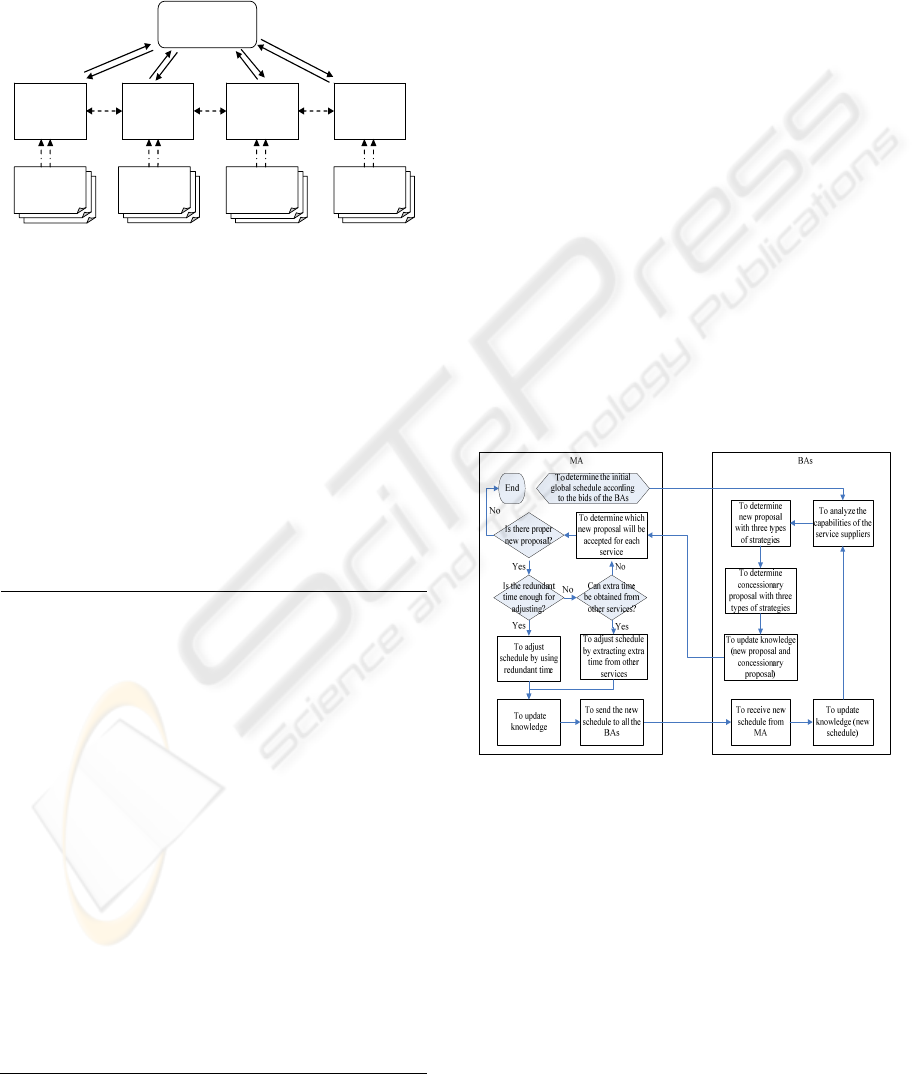
2 PROBLEM FOMULATION

A supply chain network like Wang et al. (2008) is

considered in this paper. As show in figure 1, the

supply chain network consists of an order manager,

brokers and service suppliers, and they are described

by corresponding agent roles.

Post-Process

Service Broker

(BA4)

Assemble

Service Broker

(BA3)

Preprocess

Service Broker

(BA2)

Procurement

Service Broker

(BA1)

Post-Process

Service Suppliers

Assemble Service

Suppliers

Preprocess Service

Supplier

Procurement

Service Supplier

Negotiation

Adjustment Adjustment Adjustment

Order Manager

(MA)

Bid Bid Bid Bid

Figure 1: The structure of the supply chain network.

Order Management Agent (MA) analyzes demands

of his orders and decomposes them to services. It

also chooses the suitable broker for each service by

bids and coordinates the relationship of the brokers.

Each service could be undertaken by only one

Service Broker Agent (BA). And a BA performs the

service by himself or chooses a supplier from the

available supplier set to do it. Each order has a due

date and a high punishment cost will be paid if the

delivery is delayed. MA assesses the time

requirements and start time of the services according

to the due dates of the orders and the relationship of

the services.

The relative symbols are shown in following:

set of services, a service is indexed by iI

∈

set of available suppliers for service i , a

supplier is indexed by

S∈

time constraint of service i

start time of service

service

i ’s redundant time between time

constraint of MA and time requirement of BA

{,}

mc mt

cost and time requirement of a broker to

perform service

{,}

ij ij

pc pt

Cost and time requirement of supplier

perform service

{,}

nc nt

cost and time consuming of a new proposal

for service

{,}

nfc nft

cost decreasing and time increasing of the

new proposal relative to present schedule

rate of the cost decreasing and the time

increasing in a new proposal

{,}

dc dt

cost and time consuming of a concessionary

proposal for service

{,}

dfc dft

cost increasing and time saving of the

concessionary proposal

rate of the cost increasing and the time saving

in a concessionary proposal

It is consumed that, brokers bid for the services

and an initial global schedule is determined by MA

before the interactive optimization process of supply

chain scheduling. And a BA always seek to

maximize the local profile base on the time

constraint and task requirement of MA. Thus the

local schedule of BA who takes service

i satisfies

max( )

iij

mc pc

, and

iij

mt pt= ; (1)

1ii i

mt st st

≤

− . (2)

According to (2), redundant time

satisfies

1ii i i

rt st st mt

=−−.

Based on the initial schedule, the optimal

objective of the project scheduling in supply chain is

to seek a globally optimal schedule, which is

meeting the time constraint of the orders, through

adjusting their local time constraint and start time

and changing the selection of service suppliers.

3 DISTRIBUTED OPTIMIZATION

PROCESS

A distributed optimization process of project

scheduling in supply chain base on heuristic and

agent negotiation is shown on figure 2.

SI IP

SI P R

iii

SI NP CP

Figure 2: The distributed optimization process.

The knowledge of MA relevant with supply

chain scheduling is defined as a quadruple:

,,,

DIPPR

<>, where D represents the set of the

services and their assignment;

and

represent

initial and middle schedule respectively, and the

content of them is

,{ , }

iii

st mc mt

> ;

represents the

amount of total cost decreasing of middle schedule

than initial schedule. In the beginning of negotiation,

MA provides information

SI IP=< > to the BA

who charging with service

i . In the process of

interaction, MA shares the information

SI P R=< >

with the BAs.

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

604

The knowledge of the BA who charging with

service

i is defined as a quintuple : ,,

iii

Bst=<

iii

TNTCT> , where ,{ , }

i i ij ij

BSpcpt=< > ;

T represents

the supplier who is selected in a middle schedule;

NT represent the supplier correspond to new

proposal;

CT represent the supplier correspond to

concessionary proposal. The information that a BA

shares with MA is defined as

iii

SI NP CP=< > , where

{,},{ , },

iiiiii

NP nc nt nfc nft nv=< > represents the new

proposal and

{,},{ , },

iiiiii

CP dc dt dfc dft dv=< > represents

the concessionary proposal.

3.1 Making New Proposal and

Concessionary Proposal by BA

As to the BA who takes service i , if his present

schedule is

{,}

mc mt , and the capable of suppliers

are

{,}

ij ij

pc pt ,

S∈ , then the algorithm for making

the new proposal is shown as

(1) For each supplier

S∈ , if

ij i

pc mc< , then

add supplier

into the supplier set for selection

SetForSel .

(2) Calculate the following variables for each

supplier in

SetForSel :

ij i ij

nfc mc pc=−;

ij ij i

nft pt mt=−; /

ij ij ij

nv nfc nft= ;

(3) Determine a supplier for performing service

i from SetForSel according to one of the three

strategies:

S1:

max( )

il ik

nv nv= , 0

nv > , kSetForSel∀∈ ;

S2:

max( )

il ik

nfc nfc= , 0

nfc > , kSetForSel∀∈ ;

S3:

min( )

il ik

nft nft=

nft >

, kSetForSel∀∈ ;

(4) If a supplier

is meet the condition for a

special strategy, then new proposal

{,},{ , },

iiiiii

Pncntnfcnftnv=< >

satisfies

iil

nc pc=

;

iil

nt pt= ;

iil

nfc nfc= ;

iil

nft nft

;

iil

nv nv= . Otherwise,

there is no valid new proposal.

The algorithm for making a concessionary

proposal is similar to making a new proposal. The

differences between them are the variables and the

strategies of each supplier. The variables of each

supplier of former are

ij ij i

dfc pc mc=−;

ij i ij

dft mt pt=−; /

ij ij ij

dv dfc dft= .

The strategies for determining a supplier for

performing service

i are

S1:

min( )

il ik

dv dv= , 0

dv > ,

kSetForSel∀∈

;

S2:

min( )

il ik

dfc dfc= , 0

dfc > , k SetForSel∀∈ ;

S3:

max( )

il ik

dft dft= , 0

dft > , kSetForSel∀∈ .

3.2 Schedule Adjusting by MA

Assume that the new proposal of BA who takes

service

m is selected for optimize the global

schedule. Redundant times are firstly considered for

meet the demand of adjusting. The algorithm is

(1) if

rt nft≥ , then

mm m

rt rt nft=− ; update the

knowledge of MA to adopt the new proposal of

service

; finish the adjusting process;

(2) if

rt nft

and

rt nft

∈

∑

, then reduce

other service’s redundant time for

i ;

update the knowledge of MA to adopt the new

proposal of service

m ; finish the adjusting process;

(3) if

rt nft

and

rt nft

∈

∑

, then

mm i

nft nft rt

∈

=−

∑

; to continue adjust the global

schedule by extracting extra time from other services.

The set of services that can be used to extract

time is denoted as B. The set of selected services for

extracting time is denoted as C. Then the algorithm

for adjusting by extracting extra time form other

services is shown as

(1)

min( )

dv dv= , iB

∀

∈ ;

≠

then move service n from

to C ,

else the adjusting will be finished.

(2) To determine what services in

C meet the

demand of adjusting:

dfc nfc

∈

≥

∑

, then the adoption of new

proposal is failed and the adjusting will be finished;

dfc nfc

∈

∑

and

dft at

∈

≥

∑

, then go to

step (3);

dfc nfc

∈

∑

and

dft at

∈

∑

, then go to

step (1);

(3) To adjust the global schedule by using the

services in set

C ; calculate the total cost of the

supply chain; and update the knowledge of MA.

4 COMPUTATIONAL RESULTS

We consider an example with 6 continue services for

an order and 4 suppliers for each services. The time

constraints of the services are generated by random

numbers satisfies adequate distribution in [50, 100].

The time consuming and cost for supplier

perform service

i are generated by

ij i

=+ and

()

ij i ij

CTP

+− ⋅, where the coefficients

and

are random numbers satisfies adequate

distribution in [-20,20], [250,500] and [0,100]

respectively. We create 10 instances by these

policies.

A mathematic programming model similar to

Lau et al. (Lau et al., 2006) is adopted for

centralized optimization and the model is solved by

using Lingo. The bid structure and coordination

approach of conflict in (Wang et al., 2008) are used

and realized with Java. The approach of the heuristic

AN AGENT-BASED OPTIMIZATION APPROACH FOR DISTRIBUTED PROJECT SCHEDULING IN SUPPLY

CHAIN WITH PARTIAL INFORMATION SHARING

605

of optimization present in this paper is also realized

with Java. The results of solving the instances are

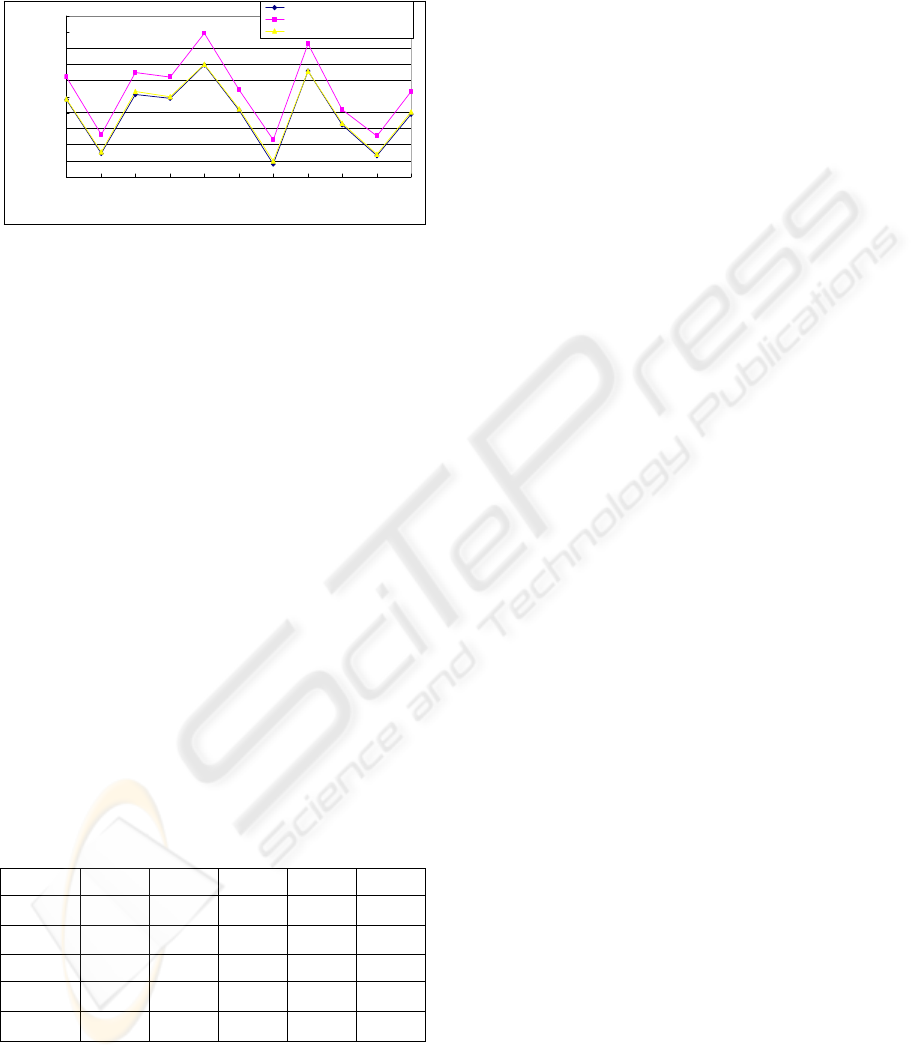
shown in figure 3.

800

900

1000

1100

1200

1300

1400

1500

1600

1700

1800

1234567891011

I nst ances

Tot al Cos t

Cent r al i zed Opt i mization

Schedul i ng by Bi ds

Heur i st i c f or O

timization

Figure 3: A comparison of the three types of scheduling.

As is shown in the figure, the results of heuristic

for optimization are considerably close to the results

of centralized optimization, and have relative high

cost decreasing than the result of Scheduling by bids.

The comparisons of optimization performance of

the three types of scheduling are shown in table 1.

There are two indexes of evaluation in the table: the

gap between scheduling by bid and centralized

optimization

()/

id Bid CO Bid

Gap TC TC TC=− , where

and

TC represent total cost of schedules obtained

by using scheduling by bid and centralized

optimization respectively; the gap between heuristic

for optimization and centralized optimization

()/

OHOCOHO

Gap TC TC TC=− where

TC represents

total cost of schedule obtained by using heuristic for

optimization. As is shown in the table, the greatest

gap between heuristic for optimization and

centralized optimization is just 2.15% and the

heuristic for optimization obtains optimal result on

instance 8. On the other hand, the gaps between

scheduling by bid and centralized optimization are

relatively wide. So we can say that the heuristic for

optimization has good performance on optimization.

Table 1: Comparisons of optimization performance of the

three types of scheduling.

1 2 3 4 5

Gap

10.06% 11.07% 9.58% 9.16% 11.74%

Gap

0.56% 1.07% 1.42% 0.62% 0.47%

6 7 8 9 10

Gap

9.65% 14.51% 10.44% 7.61% 11.71%

Gap

1.03% 2.15% 0.00% 0.81% 1.24%

5 CONCLUSIONS

Base on the description of the structure of a supply

chain network, the paper present a heuristic for

optimization of distributed project scheduling in

supply chain. The approach of scheduling base on a

heuristic and an agent negotiation architecture

through sharing partial information, including new

proposals, concessionary proposals of service

brokers and the global schedule of the order

manager. Computational experiences show that the

approach has good optimization performance by

comparing with centralized optimization and

scheduling by bids with two evaluation indexes.

ACKNOWLEDGEMENTS

This work is supported by the project of philosophy

and social science in Beijing (

S0011790200901).

REFERENCES

Banaszak, Z. A., Zaremba, M. B. Project-driven planning

and scheduling support for virtual manufacturing.

Journal of Intelligent Manufacturing, 17(6) 2006: 641-

651.

Banaszak, Z. A., Zaremba, M. B., Muszynski, W.

Constraint programming for project-driven

manufacturing. International Journal of Production

Economics, In Press, Corrected Proof

2009.

Huang, G. Q., Lau, J. S. K., Mak, K. L., Liang, L.

Distributed supply-chain project rescheduling: part I -

impacts of information-sharing strategies.

International Journal of Production Research, 43(24)

2005: 5107-5129.

Huang, G. Q., Lau, J. S. K., Mak, K. L., Liang, L.

Distributed supply-chain project rescheduling: part II-

distributed affected operations rescheduling algorithm.

International Journal of Production Research, 44

2006: 1-25.

Lau, J. S. K., Huang, G. Q., Mak, H. K. L., Liang, L.

Agent-based modeling of supply chains for distributed

scheduling. Ieee Transactions on Systems Man and

Cybernetics Part a-Systems and Humans, 36(5)

2006:

847-861.

Lecompte, T., Deschamps, J. C., Bourrieres, J. P. A data

model for generalized scheduling for virtual

enterprise.

Production Planning & Control, 11(4)

2000: 343-348.

Vairaktarakis, G., Hosseini, J. Forming partnerships in a

virtual factory.

Annals of Operations Research, 161(1)

2008: 87-102.

Wang, M., Wang, H., Vogel, D., Kumar, K., Chiu, D. K.

W. Agent-based negotiation and decision making for

dynamic supply chain formation. Engineering

Applications of Artificial Intelligence, In Press,

Corrected Proof

2008.

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

606