
A REINFORCEMENT LEARNING APPROACH FOR MULTIAGENT
NAVIGATION
Francisco Martinez-Gil, Fernando Barber, Miguel Lozano, Francisco Grimaldo
Departament d’Informatica, Universitat de Valencia, Campus de Burjassot, Burjassot, Valencia, Spain
Fernando Fernandez
Departamento de Informatica, Universidad Carlos III, Campus de Leganes, Madrid, Spain
Keywords:
Reinforcement learning, Multiagent systems, Local navigation.
Abstract:
This paper presents a Q-Learning-based multiagent system oriented to provide navigation skills to simulation
agents in virtual environments. We focus on learning local navigation behaviours from the interactions with
other agents and the environment. We adopt an environment-independent state space representation to provide
the required scalability of such kind of systems. In this way, we evaluate whether the learned action-value
functions can be transferred to other agents to increase the size of the group without loosing behavioural
quality. We explain the learning process defined and the the results of the collective behaviours obtained in a
well-known experiment in multiagent navigation: the exit of a place through a door.
1 INTRODUCTION
During last years, the most popular approaches to
multiagent navigation have been inspired in differ-
ent kind of rules (phyisical, social, etological, etc).
These systems have demostrated that it is possible to
group and to combine different rules (eg. cohesion,
obstacle avoidance (Reynolds, 1987)) to finally dis-
play high quality collective navigational behaviours
(eg. flocking). However the main drawbacks are also
known. All the rules must be defined and adjusted
manually by the engineer or author. The number of
rules required for modelling complex autonomous be-
haviours can be high, and generally they are systems
difficult to adjust when scaling the number of agents,
where some problems (eg. local minimum or dead-
locks) can appear. Beyond handwritten rules sys-
tems, other discrete techniques, as celular automata
or multi-layer grids have been also used in these do-
mains (Lozano et al., 2008) for representing different
kind of navigational maps, as they can precompute
important information for the agents when they have
to plan and to follow their paths.
In this paper we present a ReinforcementLearning
(RL) approach that consists on modelling the problem
as a sequential decision problem using Markov De-
cision Process (MDP). Reinforcement learning tech-
niques have been used successfully to find policies
for local motion behaviors without knowledge of the
environment (Kaelbling et al., 1996). It has been
also applied in cooperativetasks, where severalagents
maximizes the collective performance by maximizing
their individual rewards (Fern´andez et al., 2005). In
these cooperative tasks, like Keepaway (Stone et al.,
2005), the relationship among individual rewards and
the cooperativebehavioris typically unknown,but co-
laboration emerges from the individual behaviors.
The aim of the paper can be summarized in: a)
setting a RL multiagent local navigation problem to
simulate a single-door evacuation and b) to study the
possibility of transferring the learned behaviors from
a specific scenario to other bigger and more popu-
lated environments, which represents the basic con-
cept of scalability in this domain. We propose the use
of multiagent reinforcement learning using indepen-
dent learners to avoid the “curse of dimensionality”
of pure multiagent systems. We do not model the
problem as a single-agent RL problem to allow the
emergence of different solutions providing variabil-
ity to the simulation. We explore the scalability (to
hundreds of agents) and portability (to larger grids)
of the approach. Scalability from a reduced set of
agents to large ones is performed through the transfer
of the value functions (Taylor and Stone, 2005). We
607
Martinez-Gil F., Barber F., Lozano M., Grimaldo F. and Fernandez F. (2010).
A REINFORCEMENT LEARNING APPROACH FOR MULTIAGENT NAVIGATION.
In Proceedings of the 2nd International Conference on Agents and Artificial Intelligence - Artificial Intelligence, pages 607-610
DOI: 10.5220/0002727906070610
Copyright
c
SciTePress
show that the value functions (and hence, the policies)
learned in scenarios with a few agents can be used in
scenarios that multiplies the number of agents.
The paper has been organized as follows, section
2 describes the learning process used. In the section 3
we explain the motivation and use of the value func-
tion transfer. The section 4 shows the simulation re-
sults. The section 5 presents the main conclusions.
2 CROWD NAVIGATION AS A RL
DOMAIN
As independent learners, each agent’s learning pro-
cess can be modeled as a single-agent MDP. A MDP
(Howard, 1960) is defined as a set of states S, a
set of actions A, a stochastic transition function T :
S× A× S → ℜ and the reward function R : S × A →
ℜ that specifies the agent’s task. The agent’s ob-
jective is to find an optimal policy, that is, a map-
ping from states to actions so as to maximize the
expected sum of discounted reward, E{
∑
∞
j=0
γ
j
r
t+ j
}
where r
t+ j
is the reward received j steps into the fu-
ture. The discount factor 0 < γ < 1 sets the influ-
ence of the future rewards. The optimal action-value
function Q(s,a)
∗
stores this expected value for each
pair state-action in a discrete MDP. The Bellman op-
timality equation gives a recursive definition of the
optimal action-value function Q
∗
(s,a) = R (s,a) +
γ
∑
s
′
T(s,a, s
′
)max
a
′
∈A
Q
∗
(s
′
,a
′
). Usually the transi-
tion function T is unknown, then the optimal policy
can be learned through experience. There are several
model-free algorithms to find Q
∗
(s,a). In Q-learning
algorithm (Watkins and Dayan, 1992) the agent starts
with arbitrary values for the action-value function Q,
and updates the entry correspondent to time t (s
t
,a)
from the new state s
t+1
receiving an inmediate reward
r
t
as follows : Q(s
t
,a) = (1 − α
t
)Q(s
t
,a) + α
t
(r
t
+
γ max
a
′
∈A
Q(s
t+1
,a
′
)). This sequence converges to
Q
∗
(s,a) when all states are visited infinitely often
and the learning rate α(t) has a bounded sum of its
cuadratic value when t → ∞.
In this work we present an experiment consisting
on a group of agents that has to leave a region of
the space reaching a door placed in the middle of a
wall. This problem has two slopes. Individually, each
agent has to learn to avoid other agents, avoid to crash
against a border and learn the existing bias between
the different actions in terms of effectiveness. As a
group, the agents have to learn to leave by the exit in
an organized way.
The features that describe the state are: a) one
feature for the distance from the agent to the goal,
b) eight features for the occupancy states of the eight
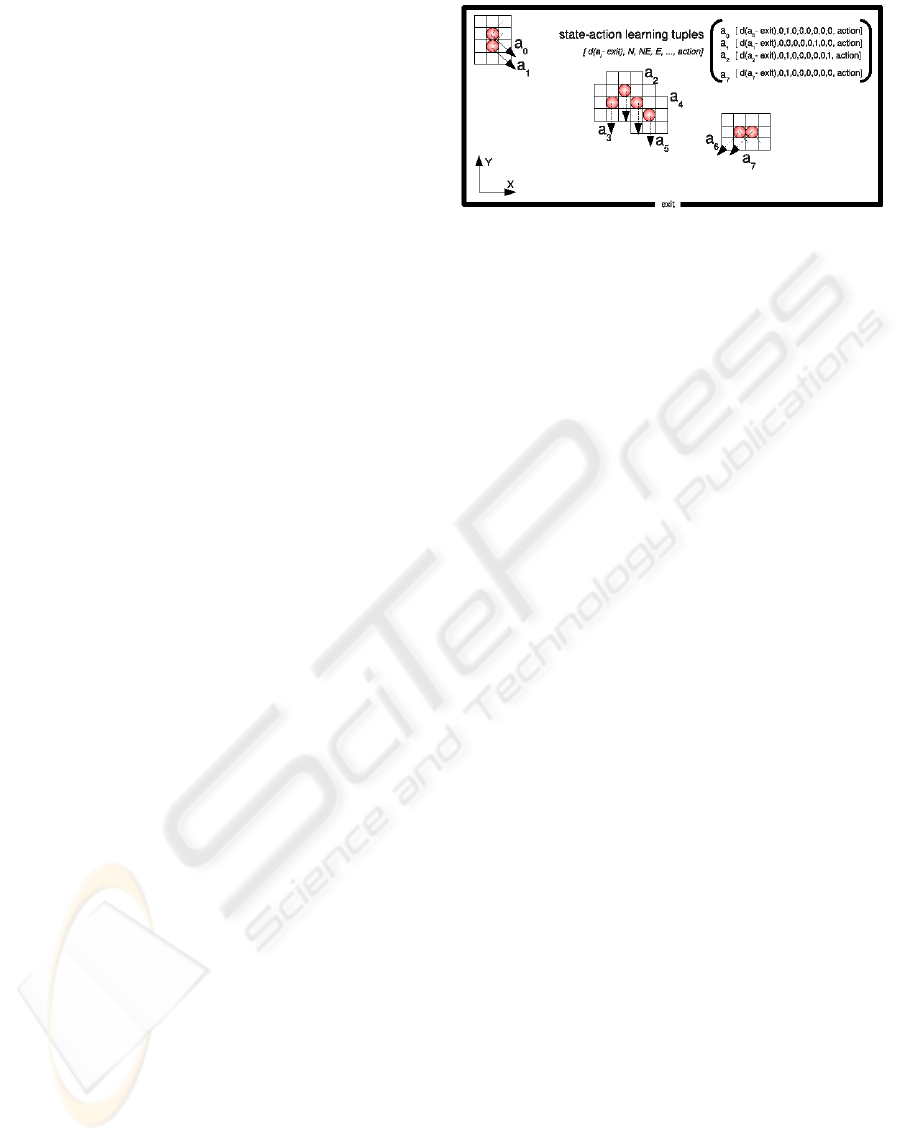
Figure 1: Multiagent learning situation example.
neighbour positions c) one feature for the orientation
respect to the goal. There is no reference to position
in the grid to allow portability. We have considered
the Chesvichev distance because it is adequate to be
used with diagonal movements. The set of actions
consists on the eight possible unitary movements to
the neighbor cells of the grid plus the action “Stay in
your place”. The agent is always oriented to the goal.
The state configuration and the actions are relative to
this orientation. For instance, in Figure 1, the arrows
represent the same action (“go to the North”) for the
different agents and all the agents sensorize the north
point in different places of the neighborhood.
We use Q-Learning with an ε-greedy exploratory
policy and exploring starts because it is a simple and
well-known model-free algorithm to converge to a
stationary deterministic optimal policy of an MDP.
The values of the learning algorithm are: the constant
step-size parameter α = 0.3, the exploration parame-
ter ε = 0.2 with an exponential decay and a discount
factor γ = 0.9. The algorithm stops when an empirical
maximum of trials is reached. If the agent reaches the
goal, the reward value is 1.0; if the agent crash against
a wall or with another agent, its immediate reward is
−2.0; if the agent consumes the maximum allowed
number of steps or cross the grid limits it is rewarded
with a value of 0. The immediate reward is always 0
for the rest of the middle states of a trial. The action-
value functions are initialized optimistically to ensure
that all the actions are explored. We have designed the
described learning problem with 20 agents, therefore
there are 20 independent learning processes.
The Figure 2 shows the incremental mean of the
expression R = R
F
γ
t
, where R
F
= {0, 1}, γ is the dis-
count factor and t is the lenght of the episode in steps.
Besides the mean reward, the curve indicates a mean
for the length of an episode in the interval [7.0,8.0]
that is coherent with the dimensions of the learning
grid. The length of an episode is the number of deci-
sions taken in this episode. The other curve displays
the averaged lenght of the episodes.
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
608

Figure 2: Mean reward curve and mean length of the
episodes curve for one agent in the learning process.
3 SCALING UP THE NUMBER OF
AGENTS
In simulation, we will use the learned value func-
tions in a larger environment with different number of
agents. We exploit the action-value functions using
the greedy action selection as the optimal policy for
an agent. Since the action and the state spaces are the
same that used for learning, no mapping is required.
However a generalization of the distance is neces-
sary because the new grids are bigger in simulation
time and agents can be placed initially farther than the
learned distances. Our generalization criteria is based
on the idea that the distance feature loses its discrimi-
natory power when it is large. Therefore the distances
higher than the MaxDist − 1 value are mapped to a
distance in the range [MaxDist − 1,MaxDist/2] using
an empirical criteria.
Each action-value function is used to animate an
incremental number of agents in the simulation en-
vironment to know their scalability. Thus then, the
number of simulated agents grows in a factor ×1, ×2,
×3,...,×10 with the following meaning: a set of 20
functions corresponding with the learning process of
20 agents will have a scaling sequence of ×1 = 20
agents, ×2 = 40 agents, ×3 = 60 agents, etc.
4 EVALUATING THE
EXPERIMENT
We have defined five evaluation parameters.
1. Parameter 1. It is the mean of random actions car-
ried out by an agent and it is related with the qual-
ity of the learned action-value function. When the
generalization process described formerly fails,
the agent chooses a random action.
Figure 3: Parameter 4 for the experiment. These data are
averages over 100 trials
2. Parameter 2. It is the total number of crashes that
happened in the simulation time. Bad learning of
states is a possible situation because convergence
is warranted only with infinite iterations and to
visit infinitelly often all the states is not guaran-
teed due to the on-line data adquisition based in
the interaction with the environment.
3. Parameter 3. It is the total number of simulated
episodes that have ended without success. When
the agent has spent a maximum number of steps
in one episode, it finishes with no success.
4. Parameter 4. It is the relative difference between
the minimum amount of steps necessary to arrive
to the exit from the initial position and the ac-
tual number of steps used. It represents the value
(
l
act
−l
min
l
min
) where l
min
is the minimum number of
actions to reach the exit from a position with a sin-
gle agent and l
act
is the number of actions actually
carried out. It gives the idea of the difference be-
tween the actual performance and the minimum
possible number of actions to reach the door. A
value of 1.0 means that the number of actions is
two times the minimum.
5. Parameter 5. It is an average density map that let
us to estimate the collective behaviour achieved
by the multiagent system during simulation. It
gives a shape of the crowd in the grid, that is a ref-
erence parameter normally considered in pedes-
trian dynamic simulations (Helbing et al., 2000).
We have performed scaling simulations up to a
scaling factor of ×10 in the number of agents, cor-
responding to a maximun of 200 agents.
Concerning the Parameter 1, the percentage of
aleatory actions used in simulation is 0% for our ex-
periment in all the scaling factors. This result shows
two facts: the generalization strategy has provided
candidates in all the cases and the Q function for states
A REINFORCEMENT LEARNING APPROACH FOR MULTIAGENT NAVIGATION
609
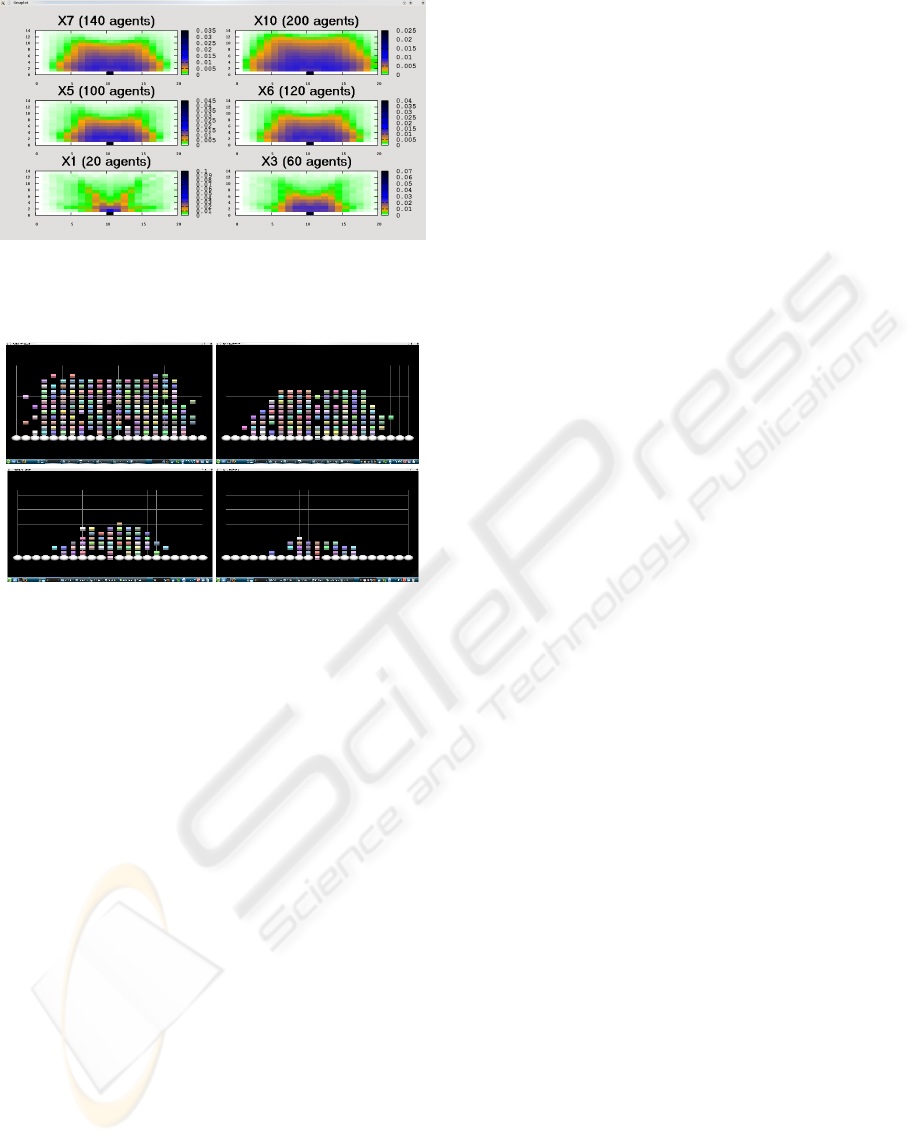
Figure 4: Average density map. The colors show densi-
ties, from low to high: white, green, orange, blue and black.
Note the wall at the bottom in white with the door in black.
Figure 5: Different moments in simulation time in a ×10
scale (200 agents). The agents are the square objects. The
elipses build the wall. The door is placed at the centre of it.
near the goals have been learned to provide an an-
swer to every query. Concerning the Parameter 2, the
number of crashes against another agent or an obsta-
cle are also 0 in all the scaling factors. It means that
the agents have learned enough to avoid crashes in all
the encountered states. The Parameter 3 hints that all
agents reach to the door. The results of these three pa-
rameters suggest that the transference of the learned
value functions to the new simulation scenarios is ad-
equate. The Figure 3 displays the results for Parame-
ter 4. In this curve, a value of 1.0 stands for an episode
twice longer than the episode carried out by a single
agent from the same initial position. The curve shows
a lineal growth of the length of the episode with the
scaling process. This lineal behavior allows us to pre-
dict the performance of the simulation in respect of
the number of simulated agents.
The Figure 4 shows the average density map ob-
tained for our experiment. It shows how the agents
are concentrating around the exit in a typical half-
circle shape. We scale from 20 agents (×1) up to 200
(×10). In all the cases, the resulting shapings have
been checked in the simulator (see Figure 5), giving
good visual results.
5 CONCLUSIONS
Our results show that RL techniques can be useful
to improve the scalability in the problem of control-
ling the navigation of crowded-oriented agents. In
our experiment up to 200 agents are managed with
a good behavior (a coherent decition sequence) using
20 learned value functions. Visual checking of the
simulations agree with the experimental curves.
The relative sensorization and the independence
of the cartesian position makes possible the scalability
of the learned process to scenarios with different sizes
and different position of the goals.
ACKNOWLEDGEMENTS
This work has been jointly supported by the Spanish
MEC and the European Commission FEDER funds,
under grants Consolider-Ingenio 2010 CSD2006-
00046 and TIN2009-14475-C04-04.
REFERENCES
Fern´andez, F., Borrajo, D., and Parker, L. (2005). A re-
inforcement learning algorithm in cooperative multi-
robot domains. Journal of Intelligent Robotics Sys-
tems, 43(2-4):161–174.
Helbing, D., Farkas, I., and Vicsek, T. (2000). Simulating
dynamical features of escape panic. Nature, 407:487.
Howard, R. A. (1960). Dynamic Programming and Markov
Processes. The MIT Press.
Kaelbling, L. P., Littman, M. L., and Moore, A. W. (1996).
Reinforcement learning: A survey. Int. Journal of Ar-
tificial Intelligence Research, 4:237–285.
Lozano, M., Morillo, P., Ordu´na, J. M., Cavero, V., and
Vigueras, G. (2008). A new system architecture for
crowd simulation. J. Networks and Comp. App.
Reynolds, C. W. (1987). Flocks, herds and schools: A dis-
tributed behavioral model. In SIGGRAPH ’87, pages
25–34, New York, NY, USA. ACM.
Stone, P., Sutton, R. S., and Kuhlmann, G. (2005). Re-
inforcement learning for RoboCup-soccer keepaway.
Adaptive Behavior, 13(3).
Taylor, M. E. and Stone, P. (2005). Behavior transfer for
value-function-based reinforcement learning. In 4th
I.J.C. Autonomous Agents and Multiagent Systems.
Watkins, C. and Dayan, P. (1992). Q-learning. Machine
Learning, 8:279–292.
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
610
