SCHEDULING SOLUTION FOR GRID META-BROKERING

USING THE PLIANT SYSTEM

J´ozsef D´aniel Dombi

Institute of Informatics, University of Szeged,

Arp´ad t´er 2., Szeged, Hungary

Attila Kert´esz

MTA SZTAKI, 1518 Budapest, P.O. Box 63, Hungary

Keywords:

Pliant system, Sigmoid function, Grid computing, Meta-Brokering.

Abstract:

In this paper we present some advanced scheduling techniques with a weighted ﬁtness function for an adaptive

Meta-Brokering Grid Service using the Pliant system, which enables a higher level utilization of the existing

grid brokers. We construct and demonstrate the efﬁciency of our new algorithms in a grid simulation envi-

ronment. The results given here demonstrate that the proposed novel scheduling technique produces better

performance scores.

1 INTRODUCTION

In 1998, a new computing infrastructure called the

Grid was born when the bible for the Grid (Kesselman

and Foster, 1998) was published by Ian Foster et. al.

Since then, Grid Computing has become an indepen-

dent ﬁeld of research; current Grid Systems are in-

tented for numerous worldwide projects, and produc-

tion Grids serve various user communities all around

the world. The emerging Web technologies have in-

ﬂuenced Grid development, and the latest solutions

from related research ﬁelds (e.g. autonomous com-

puting, artiﬁcial intelligence and peer-to-peer tech-

nologies) also need to be taken into account in order

to achieve better resource utilization and successfully

transform the currently separate production Grids to

the future Internet of Services (Report, 2006).

As the management and advantageous utilization

of highly dynamic, complex grid resources cannot

be handled by the users themselves, various grid re-

source management tools have been developed and

support different Grids. User requirements created

certain properties that resource managers now pro-

vide. This development is continuing, and users still

ﬁnd it hard to distinguish brokers and to migrate their

applications when they move to a different grid sys-

tem. Scheduling in diverse and distributed environ-

ments requires sophisticated approaches because a

high uncertainty is present at several stages of a Grid

environment. The main contribution of this paper

lies in an enhanced scheduling solution based on the

Pliant System (Dombi, 1997) that is applied to the

resource management layer of grid middleware sys-

tems.

The Pliant system is very similar to a fuzzy sys-

tem (Dombi, 1982). The difference between the two

systems lies in the choice of operators. In fuzzy the-

ory the membership function plays an important role,

although the exact deﬁnition of this function is often

not clear. In Pliant systems we use a so-called dis-

tending function, which represents a soft inequality.

In the Pliant system the various operators (conjunc-

tion, disjunction and aggregation) are closely related

to each other. We also use unary operators (negation

and modiﬁers), which are also related to the Pliant

system. In consequence, the Pliant system involves

only those operators whose relationship is clearly de-

ﬁned and the whole system is based on these identi-

ties.

In the next section we shall introduce the Pliant

system, operators and functions. In Section 3 we will

describe meta-brokering in Grids, while in Section 4

we discuss algorithms of an adaptive scheduling tech-

nique that seek to provide better scheduling in global

Grids. Section 5 describes an evaluation of our pro-

posed solution and ﬁnally, in the last section we will

Dániel Dombi J. and Kertész A. (2010).

SCHEDULING SOLUTION FOR GRID META-BROKERING USING THE PLIANT SYSTEM.

In Proceedings of the 2nd International Conference on Agents and Artiﬁcial Intelligence - Agents, pages 46-53

DOI: 10.5220/0002728500460053

 SciTePress

brieﬂy summarize our results and draw some relevant

conclusions.

2 COMPONENTS OF THE

PLIANT SYSTEM

In fuzzy logic theory (Dombi, 1982) the membership

function plays an important role. In pliant logic we

introduce a distending function with a soft inequality.

The Pliant system is a strict, monotonously increasing

t-norm and t-conorm, and the following expression is

valid for the generator function:

(x) f

(x) = 1, (1)

where f

(x) and f

(x) are the generator functions

of the conjunctive and disjunctive logical operators.

Here we use the representation theorem of the asso-

ciative equation (Aczl, 1966):

, x

, · · · , x

) = f

−1

∑

i=1

)

(2)

The generator function could be the Dombi oper-

ator (Dombi, 1982):

f(x) =

1− x

, f

−1

(x) =

1+ x

(3)

Besides the above-mentioned logical operators in

fuzzy theory, there is also another non-logical opera-

tor. The reason for this that for real world applications

it is not enough to use just conjunctive or disjunction

operators (Zimmermann, 1991). The rational form of

an aggregation operator is:

ν,ν

, · · · , x

) =

1−ν

∏

i=1

1−x

, (4)

where ν is the neutral value and ν

is the threshold

value of the corresponding negation.

The general form of the distending function is the

following:

(λ)

(x) = f

−1



−λ(x−a)



, λ ∈ R, a ∈ R (5)

Here f is the generator function of the logical con-

nectives, λ is responsible for the sharpness and a de-

notes the threshold value. The semantic meaning of

(λ)

truth(a <

x) = δ

(λ)

(x) (6)

Important properties of the distending function

are:

1. In the Pliant system f could be the generator func-

tion of the conjunctive operator or the disjunctive

operator. The form of δ

(λ)

(x) is the same in both

cases.

2. In the Pliant concept the operators and member-

ship are closely related.

2.1 Sigmoid Function

In the Dombi operator case, the distending function is

the sigmoid function (see Figure 1):

(λ)

(x) =

1+ e

−λ(x−a)

(7)

Here, it is clear that:

(λ)

(a) =

= ν

(8)



(λ)

(a)



′

(9)

(−λ)

(x) = n(σ

(λ)

(x)) if n(x) = 1− x. (10)

Figure 1: Sigmoid function.

The sigmoid function naturally maps the values to

the (0,1) interval.

2.2 Kappa function

In order to make a decision we need to deﬁne a unary

transformation for the values produced by the pliant

operator. Using pliant logic, the general form of the

modiﬁcation operators is:



1−ν

1−x



(11)

SCHEDULING SOLUTION FOR GRID META-BROKERING USING THE PLIANT SYSTEM

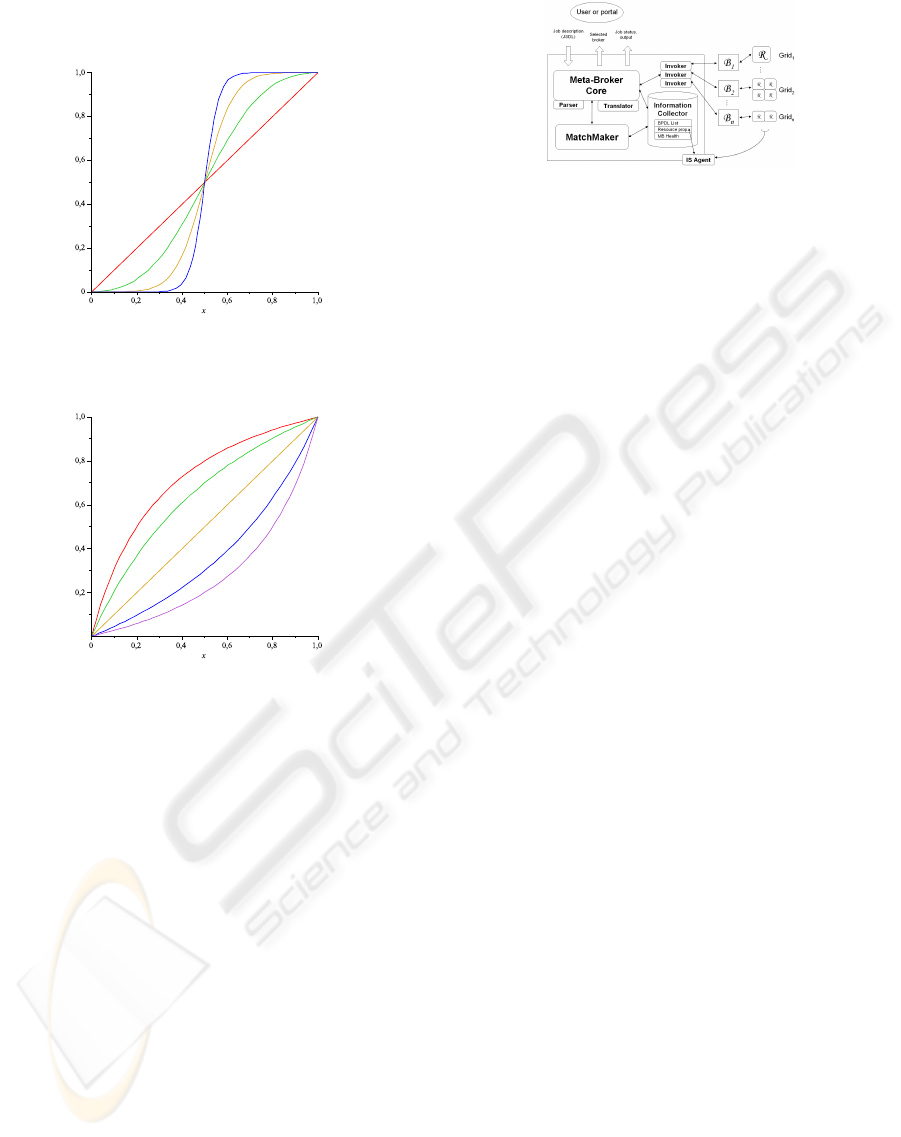
The behaviour of this function for different values

of ν nand λ can be seen in ﬁgures 2 and 3.

Figure 2: Modiﬁcation operator with the parameter values

ν = 0.5, λ = 1, 2, 4, 8.

Figure 3: Modiﬁcation operator with the parameter values

λ = 1, ν = 0.1, 0.3, 0.5,0.7, 0.8.

3 META-BROKERING IN GRID

SYSTEMS

Meta-brokering refers to a higher level of resource

management, which utilizes an existing resource or

service brokers to access various resources. In some

generalized way, it acts as a mediator between users or

higher level tools and environment-speciﬁc resource

managers. The main tasks of this component are:

to gather static and dynamic broker properties, and

to schedule user requests to lower level brokers, i.e.

match job descriptions to broker properties. Finally

the job needs to be forwarded to the selected broker.

Figure 4 provides a schematic diagram of the

Meta-Broker (MB) architecture (Kertesz and Kacsuk,

2008), including the components needed to fulﬁl the

above-mentioned tasks. Different brokers use differ-

ent service or resource speciﬁcation descriptions to

understand the user request. These documents need to

be written by the users to specify the different kinds of

Figure 4: Components of the Meta-Broker.

service-related requirements. For the resource utiliza-

tion in Grids, OGF (ogf, 1999) developed a resource

speciﬁcation language standard called JSDL (An-

jomshoaa et al., 2005). As JSDL is general enough

to describe the jobs and services of different grids and

brokers, this is the default description format of MB.

The Translator component of the Meta-Broker is re-

sponsible for translating the resource speciﬁcation de-

ﬁned by the user to the language of the appropriate

resource broker that MB selects to use for a given re-

quest. These brokers have various features for sup-

porting different user needs, hence an extendable Bro-

ker Property Description Language (BPDL) (Kertesz

and Kacsuk, 2008) is required to express metadata

about brokers and the services they provide. The

Information Collector (IC) component of MB stores

data about the accessible brokers and historical data

about previous submissions. This information tells us

whether the chosen broker is available, and/or how

reliable its services are. During broker utilization the

successful submissions and failures are tracked, and

for these events a ranking is updated for each special

attribute in the BPDL of the appropriate broker (these

attributes are listed above). In this way, the BPDL

documents represent and store the dynamic states of

the brokers. In order to support load balancing, there

is an IS Agent (IS stands for Information System) re-

porting to the IC, which regularly checks the load of

the underlying resources of each linked broker, and

stores this data. The matchmaking process consists

of the following steps: The MatchMaker (MM) com-

pares the received descriptions to the BPDL of the

registered brokers. This selection determines a group

of brokers that can provide the required service. Oth-

erwise, the request is rejected. In the second phase the

MM counts a rank for each of the remaining brokers.

This rank is calculated from the broker properties that

the IS Agent updates regularly, and from the service

completion rate that is updated in the BPDL for each

broker. When all the ranks have been counted, the list

of the brokers is ordered by these ranks. Finally the

ﬁrst broker of the priority list is selected, and the In-

voker component forwards the request to the broker.

Regarding related works, other approaches try

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

to deﬁne common protocols and interfaces among

scheduler instances enabling inter-grid usage. The

meta-scheduling project in LA Grid (Rodero, 2008)

aims to support grid applications with resources lo-

cated and managed in different domains. They de-

ﬁne broker instances with a set of functional mod-

ules. Each broker instance collects resource infor-

mation from its neighbors and saves the informa-

tion in its resource repository. The resource infor-

mation is distributed in the different grid domains

and each instance will have a view of all resources.

The Koala grid scheduler (Iosup et al., 2007) was

designed to work on DAS-2 interacting with Globus

middleware services with the main features of data

and processor co-allocation; lately it is being ex-

tended to support DAS-3 and Grid’5000. Their pol-

icy is to use a remote grid only if the local one is

saturated. They use a so-called delegated matchmak-

ing (DMM), where Koala instances delegate resource

information in a peer-to-peer manner. Gridway in-

troduces a Scheduling Architectures Taxonomy (Leal

et al., 2009). Its Multiple Meta-Scheduler Layers

use Gridway instances to communicate and interact

through grid gateways. These instances can access

resources belonging to different administrative do-

mains. They also pass user requests to another do-

main, when the current one is overloaded. Comparing

these related approaches, we can state that all of them

use a new method to expand current grid resource

management boundaries. Meta-brokering appears in

a sense that different domains are being examined as

a whole, but they rather delegate resource informa-

tion among domains, broker instances or gateways

through their own, implementation-dependent inter-

faces. Their scheduling policies focus on resource

selection by usually aggregated resource information

sharing, while our approach targets broker selection

based on broker properties and performances.

4 SCHEDULING ALGORITHMS

In the previous sections we introduced the Pliant Sys-

tem and Grid Meta-Broker, and showed how the de-

fault matchmaking process is carried out. The main

contribution of this paper is to enhance the schedul-

ing part of this matchmaking process. To achieve

this, we created a Decision Maker component based

on functions of the Pliant system, and inserted it into

the MatchMaker component of the Meta-Broker. The

ﬁrst part of the matchmaking is unchanged: the list

of the available brokers is ﬁltered according to the re-

quirements of the actual job read from its JSDL. Then

a list of the remaining brokers along with their perfor-

mance data and the background grid load are sent to

the Decision Maker in order to determine the most

suitable broker for the actual job. The scheduling

techniques and the scheduling process are described

below.

The Decision Maker uses a random number gen-

erator, and we chose a JAVA solution that generates

pseudorandom numbers. The JAVA random generator

class uses a uniform distribution and 48-bit seed and

the latter is modiﬁed by a linear congruential formula

(Knuth, 1997). We also developed a unique random

number generator which generates random numbers

with a given distribution. We call this algorithm the

generator function. In our case we deﬁned a score

value for each broker, and we created the distribution

based on the score value. For example, the broker

which has the highest score number has the biggest

chance of being chosen.

To improve the scheduling performance of the

Meta-Broker we need to send the job to the broker

that best ﬁts the requirements, and executes the job

without failures with the shortest execution time. Ev-

ery broker has four properties that the algorithm can

rely on: a success counter, a failure counter, a load

counter and the running jobs counter.

• The success counter gives the number of jobs

which had ﬁnished without any errors.

• The failure counter shows the number of failed

jobs.

• The load counter indicates the actual load of the

grid behind the broker (in percentage terms).

• The running jobs counter shows the number of

jobs sent to the broker which havenot yet ﬁnished.

We developed two different kinds of decision al-

gorithms that take into account the above-mentioned

broker properties. These algorithms deﬁne a score

number for each broker and use the generator func-

tion to select a broker. Both algorithms use the kappa

function to determine the broker’s score number.

Because the Pliant system is deﬁned in the [0, 1]

interval, we need to normalize the input value. The

two algorithms differ only in this step:

1. The ﬁrst algorithm uses a linear transformation

called Decision4.

2. The second algorithm uses the Sigmoid function

to normalize the input values, which is called De-

cision5.

It is also important to emphasize that the closer

the value is to one, the better the broker is, and if the

value is close to zero, it means that the broker is not

good. For example if the failure counter is high, both

normalization algorithms should give a value close to

SCHEDULING SOLUTION FOR GRID META-BROKERING USING THE PLIANT SYSTEM

zero because it is not a good thing if the broker has

a lot of failed jobs (see in Figure 5). The opposite of

this case is true for the success counter (see Figure 6).

Figure 5: Normalizing the failed jobs counter using Sig-

moid function.

Figure 6: Normalizing the success counter using the Sig-

moid function.

In the next step we can modify the normalized

property value by using the same Kappa function (see

Figure 7). We can also deﬁne the expected value of

the normalization via the ν and λ parameters.

Figure 7: Normalized parameter values using the Kappa

function.

To calculate the score value, we can make use of

the conjunctive or aggregation operator. After run-

ning some tests we found that we get better results if

we use the aggregation operator. In this step the result

is always a real number lying in the [0, 1] interval and

then we multiply it by 100 to get the broker’s score

number.

When the Meta-Broker is running, the ﬁrst two

broker properties (the success and failure counters)

are incremented via a feedback method that the simu-

lator (or a user or portal in real world cases) calls after

the job has ﬁnished. The third and fourth properties,

the load value and the running jobs, are handled by

the IS Agent of the Meta-Broker, queried from an in-

formation provider (Information System) of a Grid.

During a simulation this data is saved to a database

by the Broker entities of the simulator (described later

and shown in Figure 8). This means that by the time

we start the evaluation and before we receive feed-

back from ﬁnished jobs, the algorithms can only rely

on the background load and running processes of the

grids. To further enhance the scheduling we devel-

oped a training process that can be executed before

the simulation in order to initialize the ﬁrst and sec-

ond properties. This process sends a small number of

jobs with various properties to the brokers and sets the

successful and failed jobs number at the BPDLs of the

brokers. With this additional training method, we can

expect shorter execution times because we will select

more reliable brokers.

5 RESULTS

5.1 Evaluation

In order to evaluate our proposed scheduling solution,

we created a general grid simulation environment,

where all the related grid resource management en-

tities could be simulated and coordinated. The Grid-

Sim toolkit (Buyya et al., 2002) is a fully extendable,

widely used and accepted grid simulation tool. These

are the main reasons why we chose this toolkit for

our simulations. It can be used for evaluating VO-

based resource allocation, workﬂow scheduling, and

dynamic resource provisioning techniques in global

grids. It supports the modeling and simulation of het-

erogeneous grid resources, users, applications, bro-

kers and schedulers in a grid computing environment.

It provides primitives for the creation of jobs (called

gridlets), the mapping of these jobs to resources, and

their management, thus resource schedulers can be

simulated to study scheduling algorithms. GridSim

provides a multilayered design architecture based on

SimJava (Howell and Mcnab, 1998), a general pur-

pose discrete-event simulation package implemented

in Java. It is used for handling the interactions or

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

events among GridSim components. Each component

in GridSim communicates with another via message

passing operations deﬁned by SimJava.

Figure 8: Meta-Brokering simulation environment based on

GridSim.

Our general simulation architecture is shown in

Figure 8. In the bottom right hand corner we can

see the GridSim components used to simulate the grid

system. The resources can be deﬁned with differ-

ent grid-types. These resources consist of more ma-

chines, for which workloads can be set. On top of this

simulated grid infrastructure we can set up brokers.

The Broker and Simulator entities were developed by

us in order to simulate the meta-brokering process.

Brokers are extended GridUser entities. Here

• they can be connected to one or more resources;

• different properties can be assigned to these bro-

kers (agreement handling, co-allocation, advance

reservation, etc.);

• some properties may be marked as unreliable;

• various scheduling policies can be deﬁned (pre-

deﬁned ones: rnd – random resource selection,

fcpu – resources having more free cpu time or

fewer waiting jobs are selected, nfailed – re-

sources having fewer machine failures are se-

lected);

• in general resubmission is used when a job fails

due to resource failure;

• after they report to the IS Grid load database

by calling the feedback method of the Meta-

Broker with the results of the job submissions

(this database has a similar purpose to that of a

grid Information System).

The Simulator is an extended GridSim entity.

Hence

• it can generate a requested number of gridlets

(jobs) with different properties, start and run times

(length);

• it is connected to the created brokers and is able

to submit jobs to them;

• the default job distribution is the random broker

selection (where the middleware types should be

taken into account);

• in the case of a job failure a different broker is

selected for the actual job;

• it is also connected to the Grid Meta-Broker

through its Web service interface and is able to

call its matchmaking service for broker selection.

5.2 Evaluation Environment

Table 1 shows the evaluation environment used in our

evaluation. The simulation setup was derived from

real-life production grids: current grids and brokers

support only a few special properties: here we used

four. To determine the number of resources in our

Table 1: Evaluation environment setup.

Broker Scheduling Properties Resources

1. fcpu A 6

2. fcpu A

3. fcpu A 12

4. fcpu B 10

5. fcpu B

6. fcpu B 12

7. fcpu B

8. fcpu C 4

9. fcpu C 4

10. fcpu A

D 8

11. fcpu AD 10

12. fcpu AD

13. fcpu AB

14. fcpu ABC

simulated grids we compared the sizes of current pro-

duction grids (EGEE VOs, DAS3, NGS, Grid5000,

OSG, etc.). In the evaluation we utilized 14 brokers.

We submitted 1000 jobs to the system, and measured

the makespan of all the jobs. Out of the 1000 jobs

100 had no special properties, while for the rest of

the jobs four key properties were distributed in the

following way: 300 jobs had property A, 300 had B,

200 had C and 100 had D. The second column above

denotes the scheduling policies used by the brokers:

fcpu means the jobs are scheduled to the resource with

the highest free cpu time. The third column shows the

capabilities/properties (like coallocation, checkpoint-

ing) of the brokers: here we used A, B, C and D in

the simulations. The F subscript means unreliability,

a broker having the kind of property that may fail to

execute a job with the requested service with a prob-

ablity of 0.5. The fourth column contains the number

of resources utilized by a broker. As a background

SCHEDULING SOLUTION FOR GRID META-BROKERING USING THE PLIANT SYSTEM

workload, 50 jobs were submitted to each resource

by the simulation workload entities during the eval-

uation timeframe. The SDSC BLUE workload logs

were used for this purpose, taken from the Parallel

Workloads Archive (PWA, 2009).

In order to test all the features of the algorithms,

we submitted the jobs periodically: 1/3 of the jobs

were submitted at the beginning then the simulator

waited for 200 jobs to ﬁnish and update the perfor-

mances of the brokers. After this phase the simula-

tor again submitted 1/3 of all the jobs and waited for

200 more to ﬁnish. Lastly the remaining jobs (1/3

again) were submitted. In this way the broker perfor-

mance results could be updated and monitored by the

scheduling algorithms.

Figure 9: Results of Decision 4 algorithm.

In the previous section we explained how the

two algorithms called Decision4 and Decision5 (both

based on the Pliant system) work. For the evaluation

part we repeated each experiment three times. The

measured simulation results of the Decision4 algo-

rithm can be seen in Figure 9. We noticed that the

measured runtimes for the jobs were very close to

each other. When comparing the various simulation

types we always used the median: we counted the av-

erage runtime of the jobs in each of the three series

and discarded the best and the worst simulations.

A comparison of the simulation results can be seen

in Figure 10 above. In our previous paper (Kertesz

et al., 2009) we used only random number generators

to boost the Decision Maker, and proposed three al-

gorithms called Decision1, Decision2 and Decision3.

In that paper Decision3 gave the best results. This is

why we will compare our new measurements with the

results of this algorithm. We can see that for around

1/3 of the simulations, Decision3 provides better re-

sults, but the overall makespans are better for the new

algorithms.

The simulation results for the algorithms with

training can be seen in Figure 11. As we mentioned

earlier, we used a training process to initiate the per-

Figure 10: Simulation results for the three desicion algo-

rithms compared with the random decision maker.

Figure 11: Simulation results for three desicion algorithms

with training compared with the random decision maker.

formance values of the brokers before job submis-

sions. In this way, the decisions for the ﬁrst round of

jobs can be made better. Upon examining the results,

Decision4 still performs about the same as Decision3,

but Decision5 clearly overperforms the other two.

Figure 12: Simulation in the main evaluation environment.

In Figure 12 above we provide a graphical sum-

mary of the various evaluation phases. The columns

show the average values of each evaluation run with

the same parameter values. The results clearly show

that the more intelligence (more sophisticated meth-

ods) we put into the system, the better the perfor-

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

mance. The most advanced version of our proposed

meta-brokering solution is called the Decision Maker

using the algorithm called Decision5 with training.

Once the number of brokers and job properties are

sufﬁciently high to set up this Grid Meta-Broker

Service for inter-connecting several Grids, the new

scheduling algorithms will be ready to serve thou-

sands of users even under conditons of high uncer-

tainty.

6 CONCLUSIONS

The Grid Meta-Broker itself is a standalone Web-

Service that can serve both users and grid portals. The

presented enhanced scheduling solution based on Pli-

ant functions allows a higher level, interoperable bro-

kering by utilizing existing resource brokers of differ-

ent grid middleware. It gathers and utilizes meta-data

about brokers from various grid systems to establish

an adaptive meta-brokering service. We developed

a new scheduling component for this Meta-Broker

called Decision Maker that uses Pliant functions with

a random generation in order to select a good per-

forming broker for user jobs even under conditions

of high uncertainty. We evaluated our algorithms in a

grid simulation environment based on GridSim, and

performed simulations with real workload samples.

The evaluation results accord with our expected uti-

lization gains: the enhanced scheduling provided by

the revised Decision Maker results in a more efﬁcient

job execution.

ACKNOWLEDGEMENTS

This study was supported by a grant from the Euro-

pean Community’s Seventh Framework Programme

FP7/2007-2013, grant contract 215483 (S-Cube).

REFERENCES

(1999). Open grid forum website. http://www.ogf.org.

(2009). Parallel workloads archive website.

http://www.cs.huji.ac.il/labs/parallel/workload.

Aczl, J. (1966). Lectures on Functional Equations and Ap-

plications. Academic Press.

Anjomshoaa, A., Brisard, F., Drescher, M., Fellows, D.,

Ly, A., McGough, S., Pulsipher, D., and Savva,

A. (2005). Job submission description language

(jsdl) speciﬁcation, version 1.0. Technical report.

http://www.gridforum.org/documents/GFD.56.pdf.

Buyya, R., Murshed, M., and Abramson, D. (2002). Grid-

sim: A toolkit for the modeling and simulation of dis-

tributed resource management and scheduling for grid

computing. In Journal of Concurrency and Compu-

tation: Practice and Experience (CCPE, pages 1175–

1220. Wiley Press.

Dombi, J. (1982). A general class of fuzzy operators, the de

morgan class of fuzzy operators and fuzziness mea-

sures induced by fuzzy operators. Fuzzy Sets and Sys-

tems, 8.

Dombi, J. (1997). Pliant system. IEEE International Con-

ference on Intelligent Engineering System Proceed-

ings, Budapest, Hungary.

Howell, F. and Mcnab, R. (1998). Simjava: A discrete event

simulation library for java. In Proc. of the Interna-

tional Conference on Web-Based Modeling and Simu-

lation, pages 51–56.

Iosup, A., Epema, D.H.J., Tannenbaum, T., Farrellee, M.,

Livny, M. (2007). Inter-Operating Grids through Del-

egated MatchMaking. In Proc. of the International

Conference for High Performance Computing, Net-

working, Storage and Analysis (SC07), Reno, Nevada.

Kertesz, A., Dombi, J.D., Dombi, J. (2009). Adaptive

scheduling solution for grid meta-brokering. In Acta

Cybernetica, Volume 19, pp. 105–123.

Kertesz, A. and Kacsuk, P. (2008). Meta-broker for future

generation grids: A new approach for a high-level in-

teroperable resource management. In Grid Middle-

ware and Services Challenges and Solutions, pages

53–63. Springer US.

Kesselman, C. and Foster, I. (1998). The Grid: Blueprint for

a New Computing Infrastructure. Morgan Kaufmann

Publishers.

Knuth, D. E. (1997). The art of computer program-

ming, volume 2 (3rd ed.): seminumerical algo-

rithms. Addison-Wesley Longman Publishing Co.,

Inc., Boston, MA, USA.

Leal, K., Huedo, E., Llorente, I.M. (2009). A decentralized

model for scheduling independent tasks in Federated

Grids. In Future Generation Computer Systems, Vol-

ume 25, Issue 8, pp. 840–852.

Rodero, I., Guim, F., Corbalan, J., Fong, L.L., Liu, Y.G.,

Sadjadi, S.M. (2008). Looking for an Evolution of

Grid Scheduling: Meta-brokering. In Proc. of Core-

grid Workshop in Grid Middleware’07, Dresden, Ger-

many.

Report, N. G. G. (2006). Future for european grids: Grids

and service oriented knowledge utilities – vision and

research directions 2010 and beyond. Technical re-

port. ftp://ftp.cordis.lu/pub/ist/docs/grids/ngg3 eg ﬁ-

nal.pdf.

Zimmermann, H. (1991). Fuzzy Set Theory and its applica-

tions. Kluwer Academic, Dordrecht.

SCHEDULING SOLUTION FOR GRID META-BROKERING USING THE PLIANT SYSTEM