PREDICTING BURSTING STRENGTH OF PLAIN KNITTED
FABRICS USING ANN
Pelin Gurkan Ünal
Ege University, Emel Akın Vocational School, 35100 Bornova/Izmir, Turkey
Mustafa Erdem Üreyen
Anadolu University, School of Industrial Arts,26470 Eskişehir, Turkey
Diren Mecit Armakan
Ege University, Textile Engineering, Bornova/Izmir, Turkey
Keywords: Textile, Bursting strength, Plain knitted fabrics, Multi layer feed forward network.
Abstract: In this study, the effects of yarn parameters, on the bursting strength of the plain knitted fabrics were
examined with the help of artificial neural networks. In order to obtain yarns having different properties
such as tenacity, elongation, unevenness, the yarns were produced from six different types of cotton. In
addition to cotton type, yarns were produced in four different counts having three different twist
coefficients. Artificial neural network (ANN) was used to analyze the bursting strength of the plain knitted
fabrics. As independent variables, yarn properties such as tenacity, elongation, unevenness, count, twists per
inch together with the fabric property number of wales and courses per cm were chosen. For the
determination of the best network architecture, three levels of number of neurons, number of epochs,
learning rate and momentum coefficient were tried according to the orthogonal experimental design. After
the best neural network for predicting the bursting strength of the plain knitted fabrics was obtained,
statistical analysis of the obtained neural network was performed. Satisfactory results for the prediction of
the bursting strength of the plain knitted fabrics were gained as a result of the study.
1 INTRODUCTION
Knitting is one of the fabric production methods
other than weaving and non woven. In knitting,
fabric surface is formed by loops connected to each
other in wale and course directions. A knitted fabric
is supposed to have some properties according to the
fabric application area. For instance, a knitted fabric
made for underwear must have high comfort
properties. In addition to the application fields,
mechanical characteristics of knitted fabrics are very
essential in downstream processes. It will be a
problem for a knitted fabric which has deficient
mechanical properties to be processed in finishing
treatments. Among the mechanical characteristics of
knitted fabrics, bursting strength is of great
importance. Fabrics are not only exposed to forces in
the vertical and perpendicular directions but also
they are exposed to multi axial forces during the
usage. Therefore, breaking and tear strength analysis
are not enough for the determination of strength
properties of the fabrics against the multi axial
forces. As a consequence, bursting strength is
extremely important for especially knitted fabrics,
parachutes, filtration fabrics and sacks. For this
reason, estimating the bursting strength of knitted
fabrics before manufacturing is very important.
A few studies have done about the prediction of
properties of the knitted fabrics. Ertugrul and Ucar
(2000) predicted the bursting strength of cotton plain
knitted fabrics before manufacturing via using
intelligent techniques of neural network and neuro-
fuzzy approaches. Ju and Ryul (2006) examined the
effects of the structural properties of plain knitted
fabrics on the subjective perception of textures,
sensibilities, and preference among consumers by
615
Gurkan Ünal P., Erdem Üreyen M. and Mecit Armakan D. (2010).
PREDICTING BURSTING STRENGTH OF PLAIN KNITTED FABRICS USING ANN.
In Proceedings of the 2nd International Conference on Agents and Artificial Intelligence - Artificial Intelligence, pages 615-618
DOI: 10.5220/0002730706150618
Copyright
c
 SciTePress

using neural networks. The prediction of fuzz fibres
on fabric surface was studied by using regression
analysis and ANN and was found that neural
networks gave better results than regression analysis
(Ertugrul and Ucar, 2007). Park, Hwang and Kang
(2001) concentrated on the objective evaluation of
total hand value in knitted fabrics using the theory of
neural networks.
In this work, it is aimed to predict the bursting
strength of plain knitted fabrics using artificial
neural networks before manufacturing the
aforementioned fabrics with regard to the yarn
properties and fabric properties.
2 MATERIAL AND METHOD
In this study, in order to predict the bursting strength
of plain knitted fabrics, fabrics were produced in
four different yarn counts (Ne 20, Ne 25, Ne 30, and
Ne 35) having three different kinds of twist
coefficients (α
e
3.8, α
e
4.2, and α
e
4.6). In order to
obtain yarns having different tenacity, elongation
and unevenness values, the yarns were produced
from six different cotton types. Totally, seventy two
different plain knitted fabrics were produced. For the
yarn tenacity and breaking elongation tests Uster
Tensorapid tensile tester was used. Yarn unevenness
measurements were performed on Uster Tester 3.
For fabric testing, the numbers of wales and courses
per cm were counted and bursting strength
properties of each plain knitted fabric were
measured with James H. Heal TruBurst Tester.
2.1 Artificial Neural Network Design
For the prediction of bursting strength of the plain
knitted fabrics, a multi layer feed forward network
with one hidden layer was used. While bursting
strength property of the plain knitted fabrics was
used as an output, yarn count (Ne), twist
(turns/inch), yarn tensile strength (cN/tex), yarn
elongation (%), yarn unevenness (CVm%) and
number of multiplication of wales and courses per
cm
2
were used as inputs in the model. As an
activation function, a hyperbolic function
)()()(
xxxx
eeeexf
−−
+−=
was used in the hidden layer
and a linear function
xxf =)(
was used in the
input and output layers. The training was performed
in one stage via using the back propagation
algorithm;
() ( 1)
ij j i ij
to t
ω
ηδ α ω Δ= +Δ−
(1)
where
η
=
the learning rate,
δ
= the local error
gradient,
α
=
the momentum coefficient,
i
o
=
the
output of the i
th
unit.
As it is generally known, learning rate influences
the speed of the neural network. Increasing the
learning rate will cause the network either oscillate
or diverge from the true solution. Giving a too low
value for this parameter will make the network too
slow and it will be time consuming to converge on
the final outputs. The other parameter that affects the
performance of the back propagation algorithm is
the momentum coefficient. High values of
momentum coefficient ensure high speed of
convergence of the network. However, choosing too
high momentum coefficients may sometimes cause
missing the minimum error. On the other hand,
setting this parameter to a low value guarantees the
local minima and will slow down the training stage.
In the constitution of the network, the first step was
to determine the number of hidden layers and the
number of neurons in each layer. In our study, one
hidden layered network gave satisfactory results
with regard to error standard deviation, absolute
error mean and coefficient of regression. In the
second step it was aimed to determine the number of
neurons in the hidden layer. For this purpose, three
levels of number of neurons such as 3, 6 and 9, three
levels of number of epochs such as 5000, 10000 and
20000, three levels of learning rate and momentum
coefficients 0.001, 0.01, 0.1 and 0.1, 0.3, 0.5 were
tried respectively according to the orthogonal
experimental design.
As there are four parameters of neural network,
three different levels of each parameter make it
difficult and time consuming to perform full
factorial experimental design (3
4
). Thus, an
orthogonal experimental design was used. As a
result, 16 different kinds of neural networks were
tried.
3 RESULTS
According to the orthogonal experimental design,
the number of neurons were changed and found that
increasing the number of neurons increased the
regression coefficient of training and testing (Figure
1). As a result, 9 neurons in the hidden layer were
chosen.
In the back propagation, training was started at
5000 epochs and then it was increased up to 20000
epochs. However, increasing the number of epochs
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
616

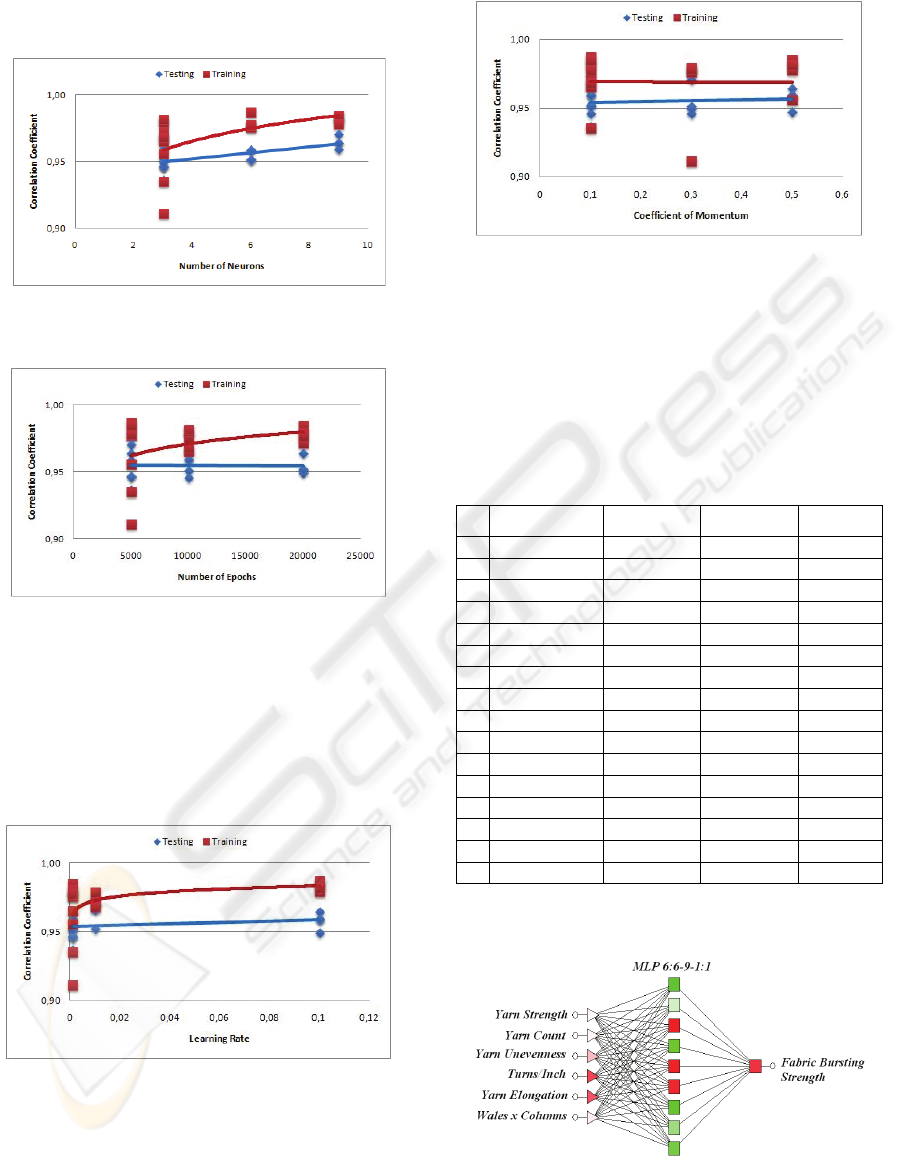
did not improve the results of testing, in fact it
decreased the prediction power of testing (Figure 2).
Figure 1: Change of correlation coefficient according to
the number of neurons.
Figure 2: Change of correlation coefficient according to
the number of epochs.
Learning rate of the algorithm was altered in
three levels according to the experimental design. It
was observed that increasing this parameter did not
make any changes in the testing results. On the other
hand, increasing this parameter increased correlation
coefficient of the training (Figure 3).
Figure 3: Change of correlation coefficient according to
learning rate.
Altering the momentum neither improved the
results of the testing nor changed the results of the
training (Figure 4).
Figure 4: Change of correlation coefficient according to
the coefficient of momentum.
According to Table 1, the best neural network
which has the high correlation and regression
coefficients and minimum mean absolute error and
standard deviation ratio for the testing stage is the
14
th
neural network.
Table 1: Testing results of the neural networks according
to the orthogonal experimental design.
N
MAE S.D.R. Corr. Regr.
1 24.1260 0.3346 0.9459 0.89
2 27.2966 0.3162 0.9640 0.93
3 30.4082 0.3578 0.9366 0.88
4 26.6822 0.3365 0.9513 0.90
5 26.4993 0.3033 0.9588 0.92
6 28.2412 0.3323 0.9524 0.91
7 30.1326 0.3399 0.9592 0.92
8 23.4184 0.3306 0.9470 0.90
9 26.0238 0.3250 0.9462 0.90
10 29.5191 0.3347 0.9492 0.90
11 27.4834 0.3300 0.9515 0.91
12 29.9798 0.3102 0.9587 0.92
13 29.9740 0.3345 0.9643 0.93
14
20.2556 0.2639 0.9707 0.94
15 25.2005 0.3214 0.9594 0.92
16 26.2121 0.2696 0.9655 0.93
N: Networks; MAE: Mean Absolute Error; SDR: Standard
Deviation Ratio; Corr: Correlation Coefficient; Regr:
Regression Coefficient
Figure 5: The best neural network obtained from the trials.
PREDICTING BURSTING STRENGTH OF PLAIN KNITTED FABRICS USING ANN
617

The best neural network after several trials is given
in Figure 5. The inputs are given according to their
impact coefficients. As a result of several trials, the
number of neurons, number of epochs, learning rate
and momentum coefficients were determined as 9,
5000, 0.01 and 0.3 respectively.
In order to observe the significance levels of
each variable in the best neural network for fabric
bursting strength, sensitivity analysis of the neural
network were performed. In this analysis, the
sensitivity is calculated as follows; the ratio of the
error in the absence of values for each variable to
total network error is calculated. This ratio means
the significance level of that particular variable to
the network. If the ratio is high, the deterioration
will be high which means that the network is more
sensitive to that particular variable. Once
sensitivities have been calculated for all variables,
they are ranked in order. Thus, the inputs are ranked
according to the calculated ratios of each variable.
Table 2 represents the sensitivity analysis results.
Table 2: Sensitivity analysis of the developed network.
Ten. Cnt Uneven Tpi Elg. WxC
Ratio
1.0010 1.0004 1.0003 1.0002 0.9999 0.9998
Rank
1 2 3 4 5 6
Ten: Yarn Strength; Cnt: Yarn Count; Uneven: Yarn Unevenness; Tpi: Turns per
inch; Elg: Yarn Elongation; WxC: Wales x Courses
As it is seen in Table 3, all the ratios of each
parameter are close to each other. However, the
most important parameter which affects fabric
bursting strength is yarn tenacity. The second
parameter is the yarn count. As it is known, fabric
bursting strength is mostly affected by the yarn
strength. Thus, this result is as expected. In addition
to yarn strength, the second parameter which affects
mostly the fabric bursting strength is yarn count. As
the yarn count changes, the properties such as yarn
strength, yarn elongation and yarn unevenness will
be changed.
The summary statistics of ANN is given in Table
3. It can be seen that even the error values of testing
are lower and estimation coefficient values are
higher. The RMSE of testing is 26.25. Since the
range of bursting strength values is 300 to 700 kPa,
this will lead a deviation in the predicted values
3.75-8.75 % of the target outputs. This result is a
desired result since in prediction of textile materials’
properties it is a difficult task to estimate the
material property with a low deviation.
4 CONCLUSIONS
In this study, it was aimed to predict the bursting
strength of the plain knitted fabrics regarding yarn
properties. In order to determine the best neural
network architecture, three levels of number of
neurons, number of epochs, learning rate and
momentum coefficient was used according to the
orthogonal experimental design. As a result of
several trials, the number of neurons, number of
epochs, learning rate and momentum coefficients
were determined as 9, 5000, 0.01 and 0.3
respectively.
It has been observed that the technique of
neural networks showed better agreement with the
prediction of the fabric bursting strength. The
developed neural network revealed a good
coincidence with the results of bursting strength.
Therefore it can be stated that the neural network
approach provides an effective skill for the
prediction of bursting strength of the plain knitted
fabrics only with a deviation of 3.75-8.75 %.
Table 3: Descriptive statistics of the best network.
Training Testing Total
Data Mean
501.75 503.96 502.30
Data S.D.
96.90 97.60 97.08
Error Mean
14.81 5.06 12.37
Error S.D.
20.03 25.76 22.01
Abs E. Mean
21.32 20.26 21.05
Mean Sq. Error
194.23 689.18 204.01
Root Mean Sq. Er.
13.94 26.25 14.28
Correlation
0.98 0.97 0.97
Regression
0.96 0.94 0.95
REFERENCES
Ertugrul, S. and Ucar, N. (2000). Predicting Bursting
Strength of Cotton Plain Knitted Fabrics Using
Intelligent Techniques, Textile Research Journal,
70(10), 845-851.
Park, S.W., Hwang, Y. and Kang B., (2001). Total handle
evaluation from selected mechanical properties of
knitted fabrics using neural network, International
Journal of Clothing Science and Technology, 13(2),
106-114.
Ucar, N. and Ertugrul, S. (2007). Prediction of Fuzz
Fibers on Fabric Surface by Using Neural Network
and Regression Analysis, Fibres&Textiles in Eastern
Europe, 15(2), 58-61.
Ju, J.G. and Ryul, H. (2006). A study on subjective
assessment of knit fabric by ANFIS, Fibers and
Polymers, 7(2), 203-212.
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
618