RELATIONAL SEQUENCE BASED CLASSIFICATION IN
MULTI-AGENT SYSTEMS
Grazia Bombini
1
, Nicola Di Mauro
1,2
, Stefano Ferilli
1,2
and Floriana Esposito
1,2
1
Dipartimento di Informatica, Universit`a degli Studi di Bari, via Orabana 4, Bari, Italy
2
Centro Interdipartimentale di Logica e Applicazioni, Universit`a degli Studi di Bari, Italy
Keywords:
Group behavior, Adversary classification, Sequence learning, Relational sequence similarity.
Abstract:
In multiagent adversarial environments, the adversary consists of a team of opponents that may interfere
with the achievement of goals. In this domain agents must be able to quickly adapt to the environment and
infer knowledge from other agents’ deportment to identify the future behaviors of opponents. We present
a relational model to characterize adversary teams based on its behavior. A team’s deportment is represent
by a set of relational sequences of basic actions extracted from their observed behaviors. Based on this, we
present a similarity measure to classify the teams’ behavior. The sequence extraction and classification are
implemented in the domain of simulated robotic soccer, and experimental results are presented.
1 INTRODUCTION
In the Agent Modeling field an essential task consists
of observing other agents and modeling their behav-
ior. The main idea is to infer knowledge from other
agents’ deportment to identify the future behaviors of
opponents. This model could be used to predict fu-
ture behavior of the other agents, in order to coordi-
nate and cooperate with them or counteract their ac-
tions. In multiagent adversarial environment, the ad-
versary consists of a team of opponents that may in-
terfere with the achievement of goals. In this domain
agents must be able to adapt to the environment, espe-
cially to the current opponents’ sequences of actions.
The observed data from this kind of environments
are inherently sequential, and hence it is necessary to
have a mechanism able to handle sequential data.
In this paper we consider the problem of identi-
fying agent behavior in complex domains where it is
necessary to consider enormous and possibly contin-
uous state and action spaces. In dynamic environ-
ments, the agents have a limited time to reason be-
fore to choose an action. For an effective adaptation,
it is necessary to capture the similarity between ob-
served behaviors, in order to adopt the most effective
strategy. Hence, a mechanism for distinguishing the
different manners and classify them to recognize dif-
ferent adversary classes is essential. From this point
of view, a key challenge is to determine what are the
sequential behaviors characterizing a team.
Our proposal is to extract from row multi-agent
observations of a dynamic and complex environment,
a set of relational sequences describing an agent be-
havior. Then, the main aim is to propose a general
method to classify different agents using those rela-
tional sequences. The goal of this paper has sev-
eral aspect: abstracting useful atomic actions (events)
from the multi-agent system log files; recognizing re-
lational sequences of events that characterize the be-
havior of a team; extracting useful features from rela-
tional sequences; defining a similarity value between
two feature-based sequence descriptions and compar-
ing different teams’ behavior by means of classifica-
tion.
2 RECOGNIZING SEQUENCES
OF ATOMIC BEHAVIORS
In an adversarial environment, the predicted behavior
of other agents is referred to as an opponent model.
One setting in which opponent modeling research has
been conducted is the RoboCup Simulation league in
the Robot World Cup Initiative
1
(Kitano et al., 1997).
In this league technologies like multi-agent collabo-
ration and adversary classification must be exploited.
1
http://www.robocup.org/
619
Bombini G., Di Mauro N., Ferilli S. and Esposito F. (2010).
RELATIONAL SEQUENCE BASED CLASSIFICATION IN MULTI-AGENT SYSTEMS.
In Proceedings of the 2nd International Conference on Agents and Artificial Intelligence - Artificial Intelligence, pages 619-622
DOI: 10.5220/0002731306190622
Copyright
c
 SciTePress

RoboCup use Soccer Server System, a client-
server system for simulating soccer. The server keeps
track of the current state of the world, and stores all
the data for a given match in a log file. This repre-
sents a stream of consecutive raw observations about
each soccer player’s position, the position of the ball,
the ball possessor, etc. at each moment of the match.
From this log streams it is possible to recognize ba-
sic actions (high-level events). Each team have se-
quences of basic actions used to form coordinated ac-
tivities which attempt to achieve the team’s goals. In
our work, we identify the following high-levelevents:
- catch(Player
n
, T): Player
n
is a goalkeeper and catches
the ball close to the penalty box at time T;
- pass(Player
n
, Player
m
, T): Player
n
kicks the ball and the
Player
m
gains possession, and both the players are of the
same team at time T;
- dribble(Player
n
, T): Player
n
moves a significant distance
since an opponent gains possession of the ball at time T;
- intercept(Player
n
, T): Player
n
gains possession at time
T, and the previous ball owner belongs of the opponent
team;
- shoot(Player
n
, T): Player
n
kick the ball close to the
penalty box of the opposite team at time T;
- outside(Player
n
, T): Player
n
kick the ball at time T, and
the ball go out of the bounds;
- goal(Player
n
, T): Player
n
kick the ball at time T, and the
ball go in the goal.
Moreover, for each event the system takes into ac-
count some description related to the actions and its
players:
- dash(Player
n
, T) : if the Player
n
at time T dashes.
- neck(Player
n
, T) : if the Player
n
at time T looks around.
- turn(Player
n
, T) : if the Player
n
at time T changes direc-
tion.
- kick(Player
n
, T) : if the Player
n
at time T is a ball owner
and kick the ball.
- chngview(Player
n
, T) : if the Player
n
at time T changes
view.
The log stream is processed to infer the high-level
events occurred during a match. An event takes place
when a ball possession changes or the ball is out of
bounds. The event sequence of one team is separated
from the events of its opponent team. Each next rec-
ognized event performed by the same team, forms the
sequence until the opposing team gains the ball pos-
session or the ball is out of bounds. An interesting se-
quence is composed at least by two successive actions
performed by players of the same team. Sequences
represent a symbolic abstraction of the row observa-
tion. A set of sequences is created for each team. This
set characterizes the observed team behavior and sep-
arated models are learned for each team. The result
of this phase is a set of the most meaningful rela-
tional sequences of recognized events that describes
each team.
3 CLASSIFYING BEHAVIOUR BY
RELATIONAL SEQUENTIAL
PATTERNS
In this section we present a method based on re-
lational pattern mining, to extract meaningful fea-
tures able to represent relational sequences and a dis-
tance function to measure the dissimilarity between
two corresponding feature vectors. Finally, those dis-
tances will be used in the k-nearest neighbor (k-NN)
algorithm to classify the adversary behavior.
Given an alphabet of symbols A , and let be k ≥ 1
a positive integer, then a k-gram (k-mers), is a se-
quence σ of symbols over A of length k (σ ∈ A
k
, |σ| =
k). For a given sequence σ = (s
1
s
2
. . . s
t
), the k-grams
of interest are all subsequences σ
′
= (s
i
s
i+1
. . . s
i+k−1
)
of length k occurring in σ.
Now we can translate the concept of k-grams to
the relational case. Given an alphabet of atoms A , a
relational k-gram is a relational sequence σ of length
k defined over A . Given a set of relational sequences
S = {σ
i
}
n
i=1
, K is the set of all relational k-grams on
all the sequences belonging to S :
K =
n
[
i=1
K
σ
i
. (1)
where K
σ
i
is the set of all relational k-grams over the
sequence σ
i
. In particular, K represents the set of all
relational features over S . We define K (α) ⊆ K , the
set of relational k-grams having a support greater than
α− 1: K (α) = {σ|σ ∈ K ∧ support(σ) ≥ α}.
In order to select the best set of features, we use
an Inductive Logic Programming (ILP) (Muggleton
and De Raedt, 1994) algorithm , based on (Espos-
ito et al., 2008), for discovering relational patterns
from sequences. It is based on a level-wise search
method, known in data mining from the APRIORI al-
gorithm (Agrawal et al., 1996). It takes into account
the sequences, tagged with the belonging class, and
the α parameter denoting the minimum support of
the patterns. It is essentially composed by two steps,
one for generating pattern candidates and the other
for evaluating their support. The level-wise algorithm
makes a breadth-first search in the lattice of patterns
ordered by a specialization relation. Starting form
the most general pattern, at each level of the lattice
the algorithm generates candidates by using the lat-
tice structure and then evaluates the frequencies of the
candidates.
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
620

Given a set of sequences S , we apply the algo-
rithm previously described (Esposito et al., 2008), to
find all the relational k-grams K (α) over the set S
with a support at least equal to α. K (α) is the or-
dered set of features F that will be used to compute
the boolean vector representation of each sequence
in the following way. Given a sequence σ ∈ S, and
F = K (α) = {ω
i
}
n
i=1
the set of relational k-grams
over S , the feature vector of σ is
V
σ
= ( f
1
(σ), f
2
(σ), ..., f
n
(σ))
where
f
i
(σ) =

1 if ω
i
⊑ σ
0 otherwise
Now, the function distance d
r
(·, ·) between two re-
lational sequences σ
1
and σ
2
is computed using the
classical Tanimoto measure (Duda et al., 2000):
d
r
1
(σ
1
, σ
2
) =
n
1σ
1
+ n
1σ
2
− 2n
1σ
12
n
1σ
1
+ n
1σ
2
− n
1σ
12
=
2(n− n
1σ
12
)
2n− n
1σ
12
(2)
where n
1σ
i
= n = |F | is the number of the features,
and n
1σ
12
= |{ f
i
| f
i
(σ
1
) = f
i
(σ
2
)}| is the number of
features with the same value in both σ
1
and σ
2
. How-
ever, this basic formulation takes into account features
not appearing (with value 0) in the sequences, and in
case of a lot of feature this can lead to underfitting.
Equation (2) may be extended in the following way:
d
r
2
(σ
1
, σ
2
) =
n
∑
i=1
f
i
(σ
1
) + f
i
(σ
2
) − 2f
i
(σ
1
) f
i
(σ
2
)
f
i
(σ
1
) + f
i
(σ
2
) − f
i
(σ
1
) f
i
(σ
2
)
(3)
where n
2σ
i
=
∑
n
j=1
f
j
(σ
i
) is the number of the features
holding in the sequence σ
i
, and n
σ
12
= |{ f
i
| f
i
(σ
1
) =
f
i
(σ
2
) = 1}| is the number of features that hold both
in σ
1
and σ
2
.
4 EXPERIMENTS
In order to evaluate our approach we analyze log files
of soccer games of the RoboCup 2008 Exercise Com-
petitions
2
. This is a preceding event for RoboCup
initiative, and includes a 2D simulation league. We
have implemented a system that is able to identify
and extract the interesting sequences of coordinated
team behaviors using the recorded observations (logs)
of this simulation games. There is an underlying as-
sumption, that the strategy of a team does not change
during the competition. We have analyzed the log
files for 4 teams, concerning to 4 matches of the com-
petition, 2 matches for each team. One adversary
2
http://robocup-cn.org/en/exercise/08/
class was created for each team by analyzing the log
files of two matches of the same team, producing a set
of relational sequences. Each sequence is made up
of interesting uninterrupted consecutive actions per-
formed by player of the same team and represents its
characteristic behavior. From the row observations of
the log files we have obtained the dataset. It is made
up of 443 sequences, defined on 7 atomic behaviors
(catch, pass, dribble, etc.) and 5 action descriptions
(neck, turn, kick, etc.). In particular, we have 112 se-
quences for the first team C0, 106 sequence for the
second team C1, 93 sequence for the third team C2
and 132 sequence for the fourth team C3.
After creating these adversary classes, the goal
was to identify which teams were playing based on
one sequence of its actions. A weighted 10-NN clas-
sifier was constructed and tested using the 10-fold
cross-validation to find the classification accuracy. In
the first step, the set K (α) of frequent k-grams has
been mined. Here, α denotes the support of each
k-gram σ ∈ K (α) corresponding to the ratio sup-
port(σ)/|S |, where S is the set of sequences in the
training set for each fold.
In this experiment, α has been set to 0.10, 0.15,
0.20 and 0.25, and the algorithm extracted, respec-
tively, 1095.2, 720.3, 501.4 and 315.2 k-grams on av-
erage on the 10 fold. The average accuracy results,
respectively, 68.39, 66.17, 68.63 and 63.9. The re-
sults for different value of α are shown in Table1.
Since in this experiment there are 4 classes to be dis-
tinguished, the accuracy on guessing should be equal
to 25%, proving that our accuracy is better then guess-
ing.
5 CONCLUSIONS AND RELATED
WORKS
In competitive domains, the knowledge about the op-
ponentcan be very advantageous. In the area of Agent
Modeling, Kaminka et al. (Kaminka et al., 2002) fo-
cus on the unsupervised autonomous learning of the
sequential behaviors of agents, from observations of
their behavior using a hybrid approach to produce
time-series of recognized atomic behaviors. These
time-series are then analyzed to find sub-sequences
characterizing each agent behavior.
Similarly to the previous approach, Lattner et
al. (Lattner et al., 2005), present a symbolic approach
based on association rule mining for pattern match-
ing on qualitative representations. The process cre-
ates patterns in dynamic scenes, based on the qual-
itative information of the environment, producing a
set of prediction rule. However, these previous works
RELATIONAL SEQUENCE BASED CLASSIFICATION IN MULTI-AGENT SYSTEMS
621

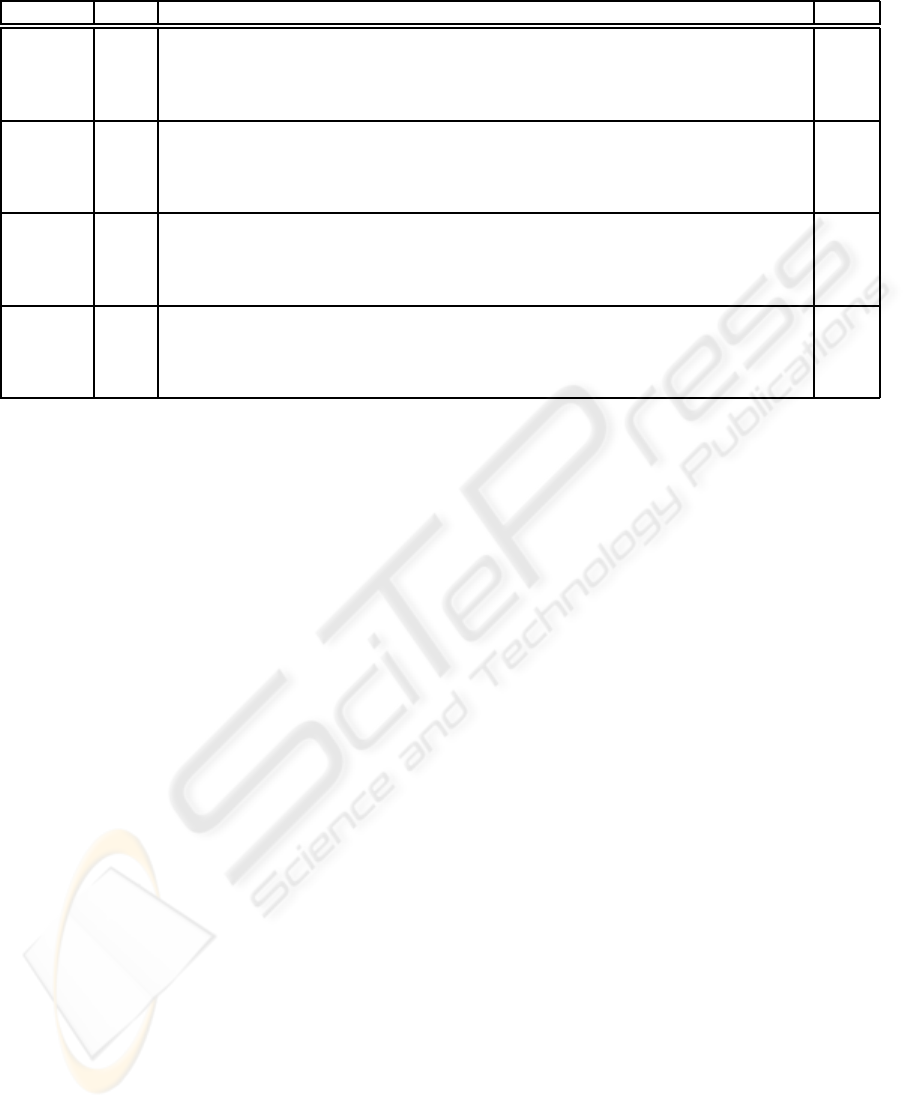
Table 1: Classification accuracy using 10-fold cross-validation.
Class F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 Mean
α = 0.25
C0 54.55 40 40 10 60 60 36.36 30 75 30 39.42
C1 70 66.67 72.73 60 22.22 10 30 60 10 30 43.16
C2 100 100 75 88.89 100 88.89 100 88.89 88.89 90 92.06
C3 66.67 76.92 53.85 84.62 84.62 100 92.31 38.46 100 85.71 78.32
α = 0.20
C0 36.36 50 40 20 50 70 72.73 40 33.33 40 42.24
C1 90 75 72.73 40 22.22 20 20 50 10 40 43.99
C2 100 100 83.33 88.89 100 88.89 100 88.89 100 90 94
C3 80 92.31 100 76.92 92.31 100 92.31 46.15 100 85.71 88.75
α = 0.15
C0 54.55 40 50 30 70 80 72.73 30 33.33 40 50.06
C1 70 66.67 63.64 50 22.22 20 20 20 10 30 36.25
C2 100 100 83.33 88.89 100 88.89 88.89 88.89 88.89 90 91.78
C3 86.67 84.62 61.54 76.92 92.31 83.33 76.92 84.62 84.62 92.86 82.44
α = 0.10
C0 63.64 20 50 30 60 50 72.73 40 33.33 30 44.97
C1 80 66.67 36.36 50 44.44 30 30 50 20 30 43.75
C2 88.89 100 58.33 88.89 100 88.89 100 100 88.89 90 91.39
C3 80 92.31 84.62 69.23 100 83.33 92.31 100 100 85.71 88.75
focused on unsupervised learning, with no ability to
classify behaviors into classes.
In this area, Riley and Veloso (Riley and Veloso,
2000) present an approach that model high-level ad-
versarial behavior by classifying the current opponent
team into predefined adversary classes. It is assumed
that opponent teams do not change strategies during
the league. Their system could classify fixed duration
windows of behavior using a set of sequence-invariant
action features. The authors use a windowing ap-
proach to extracting useful feature removing time se-
quencing from data,but this length affect the accuracy
of the classifier and its performance. To classify the
instance of observations decision tree on flat symbols
are used.
In our work, we proposed a relational model to
characterize adversary teams based on its behavior. A
team’s deportment is represent by a set of relational
sequences of basic actions extract to their observed
behaviors. Based on this, a similarity measure for
classify the teams’ behavior has been presented.
The log files used to extract the dataset, are the
results of the matches of a RoboCup competition. In
order to create winner teams, many people working
together using a great variety of technique and strate-
gies. Moreover, we create an adversary class for each
team. If two teams adopt a similar strategy, we re-
quest to the classification method to distinguish them.
A more refined method to define adversary classes,
likely could improve the classification accuracy. Ex-
perimental results proved the validity of the proposed
approach. As a future work, we will investigate meth-
ods for extracting patterns with a high discriminative
power, and we will compare different similarity func-
tions.
REFERENCES
Agrawal, R., Mannila, H., Srikant, R., Toivonen, H., and
Verkamo, A. (1996). Fast discovery of association
rules. In Advances in Knowledge Discovery and Data
Mining.
Duda, R. O., Hart, P. E., and Stork, D. G. (2000). Pattern
Classification (2nd Edition). Wiley-Interscience.
Esposito, F., Di Mauro, N., Basile, T., and Ferilli, S. (2008).
Multi-dimensional relational sequence mining. Fun-
damenta Informaticae, 89(1):23–43.
Kaminka, G. A., Fidanboylu, M., Chang, A., and Veloso,
M. M. (2002). Learning the sequential coordinated
behavior of teams from observations. In Kaminka,
G. A., Lima, P. U., and Rojas, R., editors, RoboCup,
volume 2752 of Lecture Notes in Computer Science,
pages 111–125. Springer.
Kitano, H., Tambe, M., Stone, P., Veloso, M., Coradeschi,
S., Osawa, E., Matsubara, H., Noda, I., and Asada,
M. (1997). The robocup synthetic agent challenge,97.
In International Joint Conference on Artificial Intelli-
gence (IJCAI97).
Lattner, A. D., Miene, A., Visser, U., and Herzog, O.
(2005). Sequential pattern mining for situation and
behavior prediction in simulated robotic soccer. In 9th
RoboCup International Symposium.
Muggleton, S. and De Raedt, L. (1994). Inductive logic
programming: Theory and methods. Journal of Logic
Programming, 19/20:629–679.
Riley, P. and Veloso, M. M. (2000). On behavior classifi-
cation in adversarial environments. In Parker, L. E.,
Bekey, G. A., and Barhen, J., editors, DARS, pages
371–380. Springer.
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
622