SELECTING GENES FROM GENE EXPRESSION DATA BY

USING AN ENHANCEMENT OF BINARY PARTICLE SWARM

OPTIMIZATION FOR CANCER CLASSIFICATION

Mohd Saberi Mohamad

1,2

, Sigeru Omatu

, Michifumi Yoshioka

and Safaai Deris

Department of Computer Science and Intelligent Systems, Osaka Prefecture University, Sakai, Osaka 599-8531, Japan

Department of Software Engineering, Universiti Teknologi Malaysia, 81310 Skudai, Johore, Malaysia

Keywords: Binary particle swarm optimization, Gene selection, Gene expression data, Cancer classification.

Abstract: In order to select a small subset of informative genes from gene expression data for cancer classification,

recently, many researchers are analyzing gene expression data using various computational intelligence

methods. However, due to the small number of samples compared to the huge number of genes (high-

dimension), irrelevant genes, and noisy genes, many of the computational methods face difficulties to select

the small subset. Thus, we propose an enhancement of binary particle swarm optimization to select a small

subset of informative genes that is relevant for classifying cancer samples more accurately. In this proposed

method, three approaches have been introduced to increase the probability of bits in particle’s positions to

be zero. By performing experiments on three different gene expression data sets, we have found that the

performance of the proposed method is superior to other previous related works, including the conventional

version of binary particle swarm optimization (BPSO) in terms of classification accuracy and the number of

selected genes. The proposed method also produces lower running times compared to BPSO.

1 INTRODUCTION

Recent advances in microarray technology allow

scientists to measure the expression levels of

thousands of genes simultaneously in biological

organisms and have made it possible to create

databases of cancerous tissues. It finally produces

gene expression data that contain useful information

of genomic, diagnostic, and prognostic for

researchers (Knudsen, 2002). Thus, there is a need to

select informative genes that contribute to a

cancerous state. However, the gene selection process

poses a major challenge because of the following

characteristics of gene expression data: the huge

number of genes compared to the small number of

samples (high-dimensional data), irrelevant genes,

and noisy data. To overcome this challenge, a gene

selection method is usually used to select a subset of

informative genes that maximizes classifier’s ability

to classify samples more accurately (Mohamad et

al., 2009). The advantages of gene selection has

been reported in Mohamad et al. (2009).

Recently, several gene selection methods based

on particle swarm optimization (PSO) have been

proposed to select informative genes from gene

expression data (Shen et al., 2008; Chuang et al.,

2008; Li et al., 2008). PSO is a new evolutionary

technique proposed by Kennedy and Eberhart

(1995). It is motivated from the simulation of social

behavior of organisms such as bird flocking and fish

schooling. Shen et al. (2008) have proposed a hybrid

of PSO and tabu search approaches for gene

selection. However, the results obtained by using the

hybrid method are less meaningful since the

application of tabu approaches in PSO is unable to

search a near-optimal solution in search spaces.

Next, an improved binary PSO have been proposed

by Chuang et al. (2008). This approach produced

100% classification accuracy in many data sets, but

it used a high number of selected genes (large gene

subset) to achieve the high accuracy. It uses the high

number because of the global best particle is reset to

zero position when its fitness values do not change

after three consecutive iterations. After that, Li et al.

(2008) have introduced a hybrid of PSO and genetic

algorithms (GA) for the same purpose.

Unfortunately, the accuracy result is still not high

and many genes are selected for cancer classification

Saberi Mohamad M., Omatu S., Yoshioka M. and Deris S. (2010).

SELECTING GENES FROM GENE EXPRESSION DATA BY USING AN ENHANCEMENT OF BINARY PARTICLE SWARM OPTIMIZATION FOR

CANCER CLASSIFICATION.

In Proceedings of the 2nd International Conference on Agents and Artiﬁcial Intelligence - Artiﬁcial Intelligence, pages 82-89

DOI: 10.5220/0002732300820089

 SciTePress

since there are no direct probability relations

between GA and PSO. Generally, the PSO-based

methods (Shen et al., 2008; Chuang et al., 2008; Li

et al., 2008) are intractable to efficiently produce a

small (near-optimal) subset of informative genes for

high classification accuracy. This is mainly because

the total number of genes in gene expression data is

too large (high-dimensional data).

Therefore, we propose an enhancement of binary

PSO (EPSO) to select a small (near-optimal) subset

of informative genes that is most relevant for

classifying cancer classes more accurately. In order

to test the effectiveness of our proposed method, we

apply EPSO to three gene expression data sets,

including binary-classes and multi-classes data sets.

This paper is organized as follows. In Section 2,

we briefly describe the conventional version of

binary PSO and EPSO. Section 3 presents data sets

used and experimental results. Section 4 summarizes

this paper by providing its main conclusions and

addresses future developments.

2 METHODS

2.1 The Conventional Version of

Binary PSO (BPSO)

BPSO is initialized with a population of particles. At

each iteration, all particles move in a problem space

to find the optimal solution. A particle represents a

potential solution in an n-dimensional space

(Kennedy and Eberhart, 1997). Each particle has

position and velocity vectors for directing its

movement. The position vector and velocity vector

of the ith particle in the n-dimension can be

represented as

(, ,..., )

iii i

xx x=

and

( , ,..., )

iii i

Vvv v= , respectively, where {0,1};

x ∈

i=1,2,..m (m is the total number of particles); and

d=1,2,..n (n is the dimension of data).

v is a real

number for the d-th dimension of the particle i,

where the maximum

v ,

max

(1 / 3) .Vn=×

In gene selection, the vector of particle positions

is represented by a binary bit string of length n,

where n is the total number of genes. Each position

vector

()

denotes a gene subset. If the value of

the bit is 1, it means that the corresponding gene is

selected. Otherwise, the value of 0 means that the

corresponding gene is not selected. Each particle in

the t-th iteration updates its own position and

velocity according to the following equations:

(1)()() ()( ()

()) () ( () ())

dddd

ii i

dd dd

vt wt vt crt pbestt

x t c r t gbest t x t

+= × + ×

−+ × −

(1)

((1))

Sig v t

−+

(2)

(( 1)) (),

Sig v t r t+> then (1)1;

xt+=

else

(1)0

(3)

where

c and

c are the acceleration constants in

the interval [0,2].

123

(), (), ()~ (0,1)

ddd

rtrtrt U are

random values in the range [0,1] that sampled from a

uniform distribution.

() ( (), (),..., ())

iii i

Pbest t pbest t pbest t pbest t= and

() ( (), (),..., ())

Gbest t gbest t gbest t gbest t= represent

the best previous position of the ith particle and the

global best position of the swarm (all particles),

respectively. They are assessed base on a fitness

function.

(( 1))

Sig v t

is a sigmoid function where

((1))[0,1].

Sig v t +∈

()wt

is an inertia weight and

initialized with 1.4. It is updated as follows:

(() 0.4)( ())

(1)

(0.4)

wt MAXITER Itert

MAXITER

−× −

(4)

where

AXITER

is the maximum iteration

(generation) and

()Iter t is the current iteration.

2.1.1 Investigating the Drawbacks of BPSO

and Previous PSO-based Methods

Before attempting to propose EPSO, it would be

prudent to find the limitations of BPSO and previous

PSO-based methods (Shen et al., 2008; Chuang et

al., 2008; Li et al., 2008). This subsection

investigates theoretically the limitations by

analyzing Eq. 2 and Eq. 3. These equations are

analyzed because they are most important equations

for genes selection in binary spaces. Both the

equations are also implemented in BPSO and the

PSO-based methods.

The sigmoid function (Eq. 2) represents a

probability for

()

t to be 0 or 1 ( (()0)

Px t

(()1)

Px t

). For example,

() 0,

then (()0)0.5

Sig v t == and

( ()0)0.5.

Px t ==

() 0,

then

(()0)0.5

Sig v t <<

and

( ()0)0.5.

Px t =>

SELECTING GENES FROM GENE EXPRESSION DATA BY USING AN ENHANCEMENT OF BINARY PARTICLE

SWARM OPTIMIZATION FOR CANCER CLASSIFICATION

() 0,

vt>

then

(()0)0.5

Sig v t >>

and

(()0)0.5.

Px t =<

Also note that

).1)((1)0)(( =−== txPtxP

From the analysis,

we conclude that

(()0) (()1)0.5

Px t Px t== ==

because Eq. 2 is a standard sigmoid function without

any constraint and no modification. Hence, by using

this standard sigmoid function in high-dimensional

spaces (gene expression data), it only reduces the

number of genes to about half of the total number of

genes. This is reported and proved in the section of

experimental results. Therefore, Eq. 2 and Eq.3 are

potentially being the drawbacks of BPSO and the

previous PSO-based methods in selecting a small

number of genes for producing a near-optimal

(small) subset of genes from gene expression data.

2.2 An Enhancement of Binary PSO

(EPSO)

Almost all previous works of gene expression data

researches have selected a subset of genes to obtain

excellent cancer classification. Therefore, in this

article, we propose EPSO for selecting a near-

optimal (small) subset of genes. It is proposed to

overcome the limitations of BPSO and previous

PSO-based methods (Shen et al., 2008; Chuang et

al., 2008, Li et al., 2008). EPSO in our work differs

from BPSO and the PSO-based methods on three

parts: 1) we introduce a scalar quantity that called

particles’ speed

()

; 2) we propose a rule for

updating

(1)

xt+ ; 3) we modify the existing

sigmoid function, whereas BPSO and the PSO-based

methods have used the original rule (Eq. 3) and the

standard sigmoid function (Eq.2), and no particles’

speed implementation. The particles’ speed, rule,

and sigmoid function are introduced in order to:

 increase the probability of

(1)0

(( ( 1) 0))

Px t+= .

 reduce the probability of (1)1

(( ( 1) 1))

Px t+=

The increased and decreased probability values

cause a small number of genes are selected and

grouped into a gene subset.

(1)1

xt+= means that

the corresponding gene is selected. Otherwise,

(1)0

xt+= represents that the corresponding gene

is not selected.

Definition 1.

is a speed or length or magnitude of

for the particle i. In a real Euclidean space

ℜ

where

ℜ

denotes the field of real numbers, and n is

the dimension of

ℜ

can be derived by the

Euclidean norm as follows:

() ( ) ( )

22 2

...

ii i i i

sV v v v== + ++

(5)

Therefore, the following properties of

are crucial:

 non-negativity:

s ≥

 definiteness:

if and only if 0;

V =

 homogeneity:

iii

VVs

αα

== where 0;

≥

 the triangle inequality:

11ii i i

VV V V

+≤+

where

and

11ii

The particles’ speed, rule, and sigmoid function are

proposed as follows:

(1) () () () ( ()

()) () ( () ())

ii i

twtstcrtdistPbestt

Xt crt distGbestt Xt

+= × + ×

−+ × −

(6)

5( 1)

(( 1))

Sig s t

−+

subject to

(1)0

≥

(7)

(( 1)) (),

Sig s t r t+> then (1)0;

xt+=

else

(1)1

(8)

where

(1)

represents the speed of the particle i

for the t+1 iteration, whereas in BPSO and previous

PSO-based methods (Eq. 1, Eq. 2, and Eq. 3),

(1)

represents a single element of a particle

velocity vector for the particle i. In EPSO, Eq. 6, Eq.

7, and Eq. 8 are used to replace Eq. 1, Eq. 2, and Eq.

3, respectively.

(1)

is the rate at which the

particle i changes its position. Based on Definition 1,

the most important property of

(1)

st+ is

(1)0.

≥

Hence,

(1)

is used instead of

(1)

so that its positive value can increase

((1)0).

Px t+=

In Eq. 6, the calculation for updating

(1)

mainly based on the distance between

()

Pbest t

and

()

t ( ( () ())),

dist Pbest t X t− and the distance

between

()Gbest t and ()

t ( ( ( ) ( ))),

dist Gbest t X t−

whereas the original formula (Eq. 1) is used to

calculate

(1)

and it is essentially based on the

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

()

(())

Sig v t

−

0.5

(()1)

Px t

(()0)

Px t =

()

(())

Sig v t

2 -2

)

0.5

2 -2

)

5()

(())

Sig s t

−

(()0)

Px t =

(()1)

Px t =

()

The area of

unsatisfied

() 0

st≥

(())

Sig s t

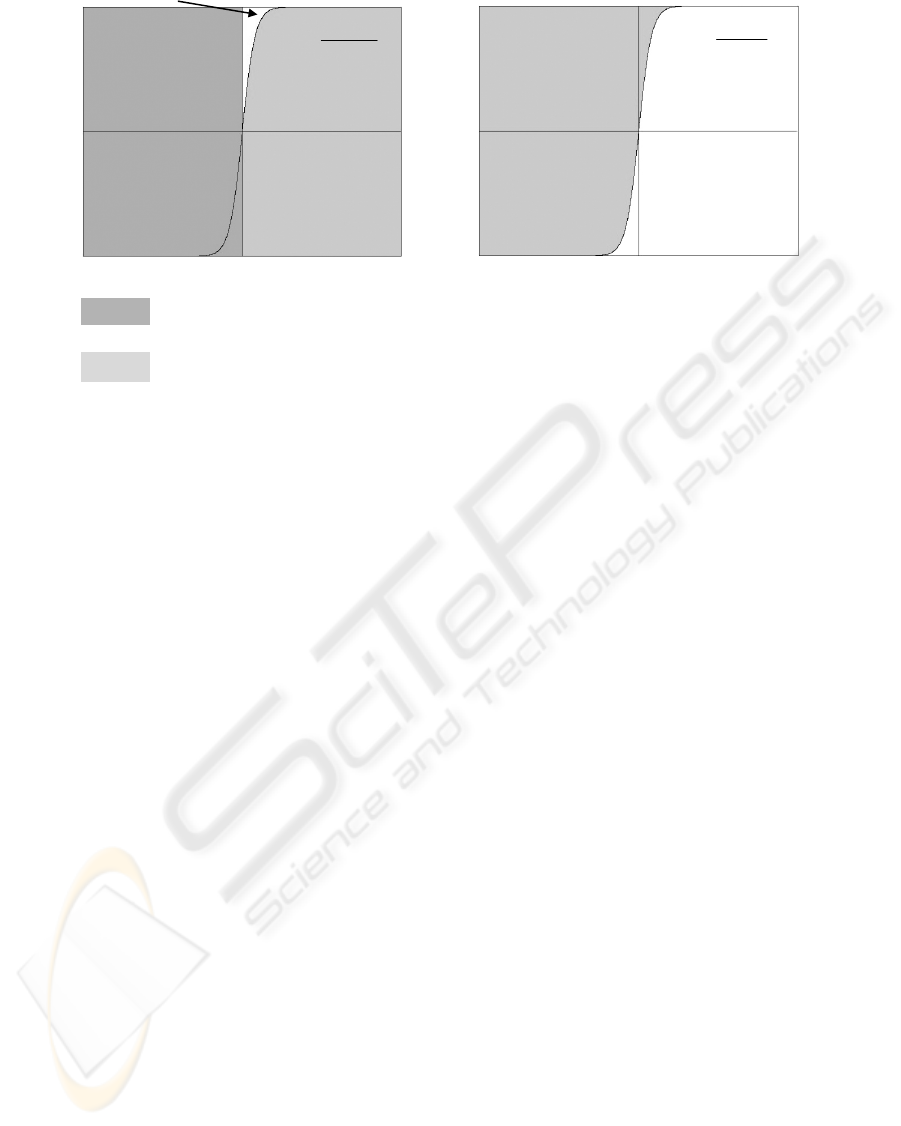
Figure 1: The areas of unsatisfied

() 0,

st≥

(()0)

Px t

and

(()1)

Px t

in a) EPSO; b) BPSO.

difference between ()

Gbest t and ().

t The

distances are used in the calculation for updating

(1)

st+ in order to always satisfy the property of

(1),

st+

namely

(( 1) 0)

st+≥

and finally increase

((1)0).

Px t+= Subsection 2.2.1 explains how to

calculate the distance between two positions of two

particles, e.g.,

( ( ) ( )).

dist Gbest t X t−

Theorem 1. Equations (6-8) and

() 0

st≥

increase

(()0)

Px t = because the minimum value for

(()0)

Px t = is 0.5 when () 0

(min ( ( ) 0) 0.5).

Px t =≥

Meanwhile, they decrease the

maximum value for

(()1)

Px t = to 0.5

(max ( ( ) 1) 0.5).

Px t =≤ Therefore, if () 0,

st> then

(()0) 0.5

Px t =>>

and

(()1) 0.5.

Px t =<<

Proof.

()⇒ Figure 1 shows that a) Equations (6-8)

and

() 0

st≥ in EPSO increase (()0);

Px t = b)

Equations (1-3) in BPSO yield

( ( ) 0) ( ( ) 1) 0.5.

Px t Px t== == For example, the

calculations for

(()0)

Px t = and (()1)

Px t = in Fig.

2(a) are shown as follows:

() 1,

st= then ( ( ) 0) 0.993307

Px t == and

( ( ) 1) 1 ( ( ) 0) 0.006693.

Px t Px t==− = =

if () 2,

st= then ( ( ) 0) 0.999955

Px t == and

( ( ) 1) 1 ( ( ) 0) 0.000045.

Px t Px t==− = =

Moreover, the modified sigmoid function (Eq. 7)

generates higher

(()0)

Px t = compared to the

standard sigmoid function (Eq. 2). For example, the

calculations for

(()0)

Px t

and (()1)

Px t = in Fig.

2(b) are shown as follows:

() 1,

then ( ( ) 0) 0.731059

Px t == and

( ( ) 1) 1 ( ( ) 0) 0.268941.

Px t Px t==− = =

() 2,

then ( ( ) 0) 0.880797

Px t == and

( ( ) 1) 1 ( ( ) 0) 0.119203.

Px t Px t==− = =

The high probability of

() 0

xt= (( () 0))

Px t =

causes a small number of genes are selected in order

to produce a near-optimal (small) gene subset from

high-dimensional data (gene expression data).

Hence, EPSO is proposed to overcome the

limitations of BPSO and the previous PSO-based

methods, and finally produce a small subset of

informative genes.

2.2.1 The Calculation of the Distance of Two

Particles’ Positions

The number of different bits between two particles

relates to the difference between their positions. For

example,

( ) [0011101000]Gbest t

and

( ) [1110110100].

The difference between

()Gbest t and

()

is [ 1 1010 11 100].

−

−−− The value

of 1 indicates that compared with the best position,

this bit (gene) should be selected, but it is not

selected, which may decrease classification quality

Legends:

The area of unsatisfied () 0.

st≥

The area of

(()0).

Px t =

The area of (()1).

Px t =

SELECTING GENES FROM GENE EXPRESSION DATA BY USING AN ENHANCEMENT OF BINARY PARTICLE

SWARM OPTIMIZATION FOR CANCER CLASSIFICATION

and lead to a lower fitness value. In contrast, a value

of -1 indicates that, compared with the best position,

this bit should not be selected, but it is selected. The

selection of irrelevant genes makes the length of the

subset longer and leads to a lower fitness value.

Assume that the number of 1 is

,a whereas the

number of -1 is

.b We use the absolute value of

ab− (| |)ab− to express the distance between two

positions. In this example, the distance between

()Gbest t and

()

(()())|||24|2.

dist Gbest t X t a b− =−=−=

2.2.2 Fitness Functions

The fitness value of a particle (a gene subset) is

calculated as follows:

() ()(( ())/)

ii i

fitness X w A X w n R X n=× + −

(9)

in which

() 0,1

AX ∈

⎡⎤

⎣⎦

is leave-one-out-cross-

validation (LOOCV) classification accuracy that

uses the only genes in a gene subset

().

This

accuracy is provided by support vector machine

classifiers (SVM).

()

X is the number of selected

genes in

n is the total number of genes for each

sample.

w and

w are two priority weights

corresponding to the importance of accuracy and the

number of selected genes, respectively, where

[0.1,0.9]w ∈

and

1ww=−

3 EXPERIMENTS

3.1 Data Sets and Experimental Setup

The gene expression data sets used in this article are

summarized in Table 1. They included binary-

classes and multi-classes data sets.

Table 1: The summary of gene expression data sets.

Data Sets

Number of

Samples

Number of

Genes

Number of

Classes

Leukemia 72 7,129 2

Colon 62 2,000 2

SRBCT 83 2,308 4

Note:

SRBCT = small round blue cell tumors.

DB = database.

DB Leukemia: http://www.broad.mit.edu/cgi-bin/cancer/datasets.cgi

DB Colon: http://microarray.princeton.edu/oncology/affydata/

index.html

DB SRBCT: http://research.nhgri.nih.gov/microarray/Supplement

All experimental results reported in this article are

experimented in Rocks Linux version 4.2.1

(Cydonia) on the IBM xSeries 335 (cluster nodes)

that contains 13 compute-nodes. Each compute-node

has four high performances 3.0GHz Intel Xeon

CPUs with 512MB of memories. Thus, the total

number of CPUs for the 13 compute-nodes is 52. In

order to make sure the running time of every run

using the same capacity of CPUs usage, each run has

been independently experimented on only one CPU.

This situation is important because the comparison

of running times between EPSO and BPSO is

conducted for evaluation of their performances.

Table 2: Parameter settings for EPSO and BPSO.

Parameters Values

The number of particles 100

The number of iterations (generations) 500

w 0.8

w 0.2

c 2

Experimental results that produced by EPSO are

compared with an experimental method (BPSO) and

other previous PSO-based methods for objective

comparisons (Shen et al., 2008; Chuang et al., 2008,

Li et al., 2008). SVM is used to measure LOOCV

accuracy on gene subsets that produced by EPSO

and BPSO. In order to avoid selection bias, the

implementation of LOOCV is in exactly the same

way as did by Chuang et al. (2008) where the only

one cross-validation cycle (outer loop), namely

LOOCV is used, not two nested ones. Several

experiments are independently conducted 10 times

on each data set using EPSO and BPSO. Next, an

average result of the 10 independent runs is

obtained. Two criteria following their importance

are considered to evaluate the performances of

EPSO and BPSO: LOOCV accuracy and the number

of selected genes. Additionally, running times are also

measured for the comparison between EPSO and

BPSO. High accuracy and the small number of

selected genes are needed to obtain an excellent

performance. Table 2 contains parameter values for

EPSO and BPSO. These values are chosen based on

the results of preliminary runs.

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

Table 3: Experimental Results for each Run Using EPSO on Leukemia, Colon, and SRBCT Data Sets.

Run#

Leukemia Colon SRBCT

#Acc

(%)

#Selected

Genes

#Time

#Acc

(%)

#Selected

Genes

#Time

#Acc

(%)

#Selected

Genes

#Time

1 100 55 7.61 93.55 17 5.16 100 33 9.91

2 100 65 7.37 93.55 11 4.93 100 26 9.91

3 100 65 7.40 95.16 22 4.98 100 25 10.36

100 70 7.42 96.77 22 4.94 100 26 10.37

100 51 7.52 98.39 23 5.06 100 31 7.31

6 100 62 7.48 95.16 15 5.07 100 22 7.31

7 100 58 7.43 93.55 27 5.00 100 26 10.33

8 100 61 7.45 95.16 29 5.02

100 21 10.32

9 100 63 7.46 93.55 20 5.03 100 29 10.24

10 100 67 7.46 91.94 16 5.02 100 22 10.24

Average

± S.D.

100

± 0

61.70

± 5.72

7.46

± 0.67

94.68

± 1.87

20.20

± 5.55

5.02

± 0.07

100

± 0

26.10

± 3.96

9.63

± 1.24

ote: The result of the best subsets is shown in the shaded cells. It is selected based on the following priority criteria: 1) the highest classification

ccuracy; 2) the smallest number of selected genes; 3) the lowest running time. #Acc and S.D. denote the classification accuracy and the standard

eviation, respectively, whereas #Selected Genes and Run# represent the number of selected genes and a run number, respectively. #Time stands for

unning time.

Table 4: Comparative experimental results of EPSO and BPSO.

Data

Method

Evaluation

EPSO BPSO

Best #Ave S.D Best #Ave S.D

Leukemia

#Acc (%)

100 100 0 98.61 98.61 0

#Genes

51 61.70 5.72 3488 3528.75 26.83

#Time

7.52 7.46 0.67 261.34 261.41 0.18

Colon

#Acc (%)

98.39 94.68 1.87 90.32 88.55 0.92

#Genes

23 20.20 5.55 982 985.00 25.22

#Time

5.06 5.02 0.07 64.45 64.63 0.18

SRBCT

#Acc (%)

100 100 0 100 100 0

#Genes

21 26.10 3.96 1076 1098.33 12.46

#Time

10.32 9.63 1.24 136.81 136.87 0.06

ote: The best result of each data set is shown in the shaded cells. It is selected based on the following priority criteria:

1) the highest classification accuracy; 2) the smallest number of selected genes; 3) the lowest running time.

Table 5: A comparison between our method (EPSO) and previous PSO-based methods.

Data

Method

Evaluation

EPSO

IBPSO

(Chuang

et al., 2008)

PSOTS

(Shen et al., 2008)

PSOGA

(Li et al., 2008)

Leukemia

#Acc (%)

(100) 100 (98.61) (95.10)

#Genes (61.70) 1034 (7) (21)

Colon

#Acc (%)

(94.68)

(93.55) (88.7)

#Genes

(20.20)

- (8) (16.8)

SRBCT

#Acc (%)

(100)

100 - -

#Genes

(26.10)

431 - -

Note: The result of the best subsets is shown in the shaded cells. It is selected based on the following priority criteria: 1) the highest classification

accuracy; 2) the smallest number of selected genes. ‘-‘ means that a result is not reported in the previous related work. A result in ‘( )’ denotes an

average result.

IBPSO = An improved binary PSO.

PSOGA = A hybrid of PSO and GA.

PSOTS = A hybrid of PSO and tabu search.

GPSO = Geometric PSO.

SELECTING GENES FROM GENE EXPRESSION DATA BY USING AN ENHANCEMENT OF BINARY PARTICLE

SWARM OPTIMIZATION FOR CANCER CLASSIFICATION

3.2 Experimental Results

Based on the standard deviation of classification

accuracy in Table 3, results that produced by EPSO

were consistent on all data sets. Interestingly, all

runs have achieved 100% LOOCV accuracy with

less than 71 selected genes on the Leukemia and

SRBCT the data sets. Moreover, over 91%

classification accuracies have been obtained on the

Colon data set. This means that EPSO has efficiently

selected and produced a near-optimal gene subset

from high-dimensional data (gene expression data).

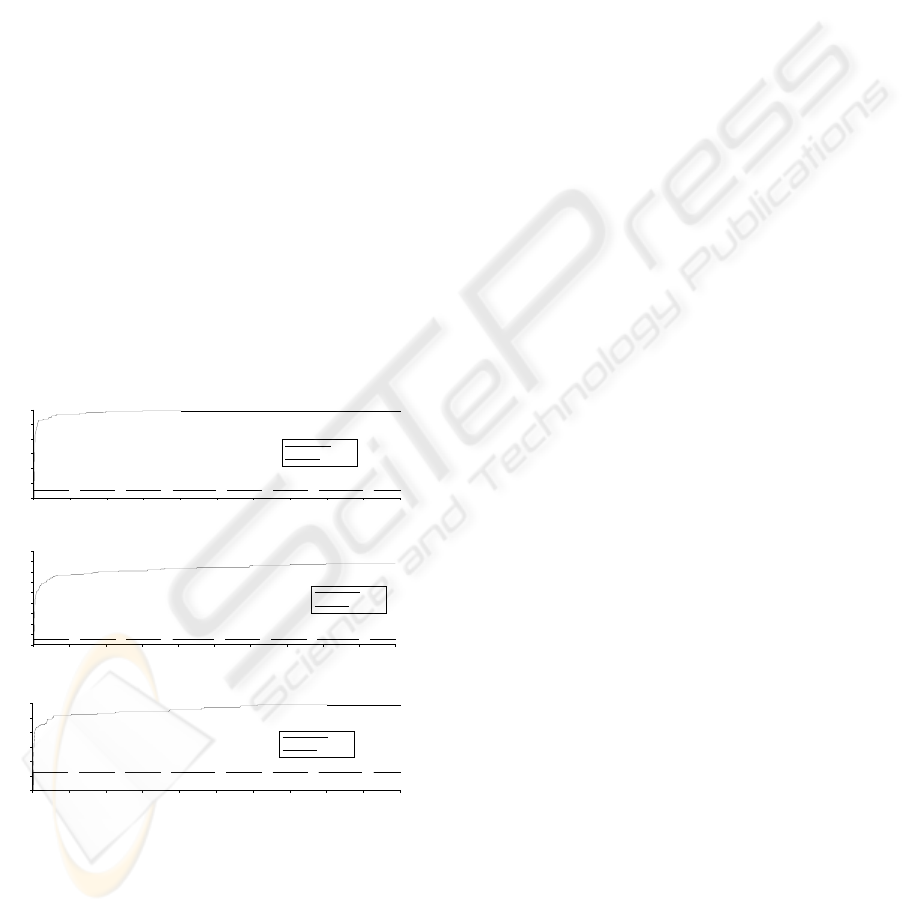
Figure 2 shows that the averages of fitness

values of EPSO increase dramatically after a few

generations on all the data sets. A high fitness value

is obtained by a combination between a high

classification rate and a small number (subset) of

selected genes. The condition of the proposed

particles’ speed that should always be positive real

numbers started in the initialization method, the new

rule for updating particle’s positions, and the

modified sigmoid function provoke the early

convergence of EPSO. In contrast, the averages of

fitness values of BPSO was no improvement until

the last generation due to

( ( ) 0) ( ( ) 1) 0.5.

Px t Px t== ==

Leukaemia Data Set

0.88

0.9

0.92

0.94

0.96

0.98

0 50 100 150 200 250 300 350 400 450 500

Generation

Fitness

EPSO

BPSO

SRBCT Data Set

0.88

0.9

0.92

0.94

0.96

0.98

0 50 100 150 200 250 300 350 400 450 500

Generation

Fitness

EPSO

BPSO

Colon Data Set

0.8

0.82

0.84

0.86

0.88

0.9

0.92

0.94

0.96

0.98

0 50 100 150 200 250 300 350 400 450 500

Generation

Fitness

EPSO

BPSO

Figure 2: The relation between the average of fitness

values (10 runs on average) and the number of generations

for EPSO and BPSO.

According to the Table 4, overall, it is

worthwhile to mention that the classification

accuracy of EPSO are superior to BPSO in terms of

the best, average, and standard deviation results on

all the data sets.. Moreover, EPSO also produces a

smaller number of genes compared to BPSO. The

running times of EPSO are lower than BPSO in all

the data sets. EPSO can reduce its running times

because of the following reasons:

 EPSO selects the smaller number of genes

compared to BPSO;

 The computation of SVM is fast because it uses

the small number of features (genes) that

selected by EPSO for classification process;

 EPSO only uses the speed of a particle for

comparing with

()

rt, whereas BPSO practices

all elements of a particle’s velocity vector for the

comparison.

For an objective comparison, we compare our

work with previous related works that used PSO-

based methods in their proposed methods (Shen et

al., 2008; Chuang et al., 2008; Li et al., 2008). It is

shown in Table 5. For all the data sets, the averages

of classification accuracies of our work were higher

than the previous works. Our work also have

resulted the smaller averages of the number of

selected genes on the data sets compared to the

previous works. The latest previous work also came

up with the similar LOOCV results (100%) to ours

on the Leukemia and SRBCT data sets, but they

used many genes (more than 400 genes) to obtain

the same results (Chuang et al., 2008). Moreover,

they could not have statistically meaningful

conclusions because their experimental results were

obtained by only one independent run on each data

set, and not based on average results. The average

results are important since their proposed method is

a stochastic approach. Additionally, in their

approach, the global best particles’ position is reset

to zero position when its fitness values do not

change after three successive iterations.

Theoretically, their approach is almost impossible to

result a near-optimal gene subset from high-

dimensional spaces (high-dimension data) because

the global best particles’ position should make a new

exploration and exploitation for searching the near-

optimal solution after its position reset to zero.

Overall, our work has outperformed the previous

related works in terms of LOOCV accuracy and the

number of selected genes.

According to Fig. 3 and Tables 3-5, EPSO is

reliable for gene selection since it has produced the

near-optimal solution from gene expression data.

This is due to the proposed particles’ speed, the

introduced rule, and the modified sigmoid function

increase the probability

(1)0

xt+=

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

(( ( 1) 0))

Px t+=

. This high probability causes the

selection of a small number of informative genes

and finally produces a near-optimal subset (a small

subset of informative genes with high classification

accuracy) for cancer classification. The particles’

speed is introduced to provide the rate at which a

particle changes its position, whereas the rule is

proposed to update particle’s positions. The sigmoid

function is modified for increasing the probability of

bits in particle’s positions to be zero.

4 CONCLUSIONS

In this paper, EPSO has been proposed for gene

selection on three gene expression data sets. Overall,

based on the experimental results, the performance

of EPSO was superior to BPSO and PSO-based

methods that proposed by previous related works in

terms of classification accuracy and the number of

selected genes. EPSO was excellent because the

probability

(1)0

xt+=

has been increased by the

proposed particles’ speed, the introduced rule, and

the modified sigmoid function. The particles’ speed,

the introduced rule, and the modified function have

been proposed in order to yield a near-optimal

subset of genes for better cancer classification.

EPSO also obtains lower running times because it

selects the small number of genes compared to

BPSO. For future works, a modified representation

of particle’s positions in PSO will be proposed to

reduce the number of genes subsets in solution

spaces.

REFERENCES

Chuang, L. Y., Chang, H. W., Tu, C. J. and Yang, C. H.

(2008). Improved Binary PSO for Feature Selection

Using Gene Expression Data.

Computational Biology

and Chemistry

, 32, 29-38.

doi:10.1016/j.compbiolchem.2007.09.005

Kennedy, J. and Eberhart, R. 1995. Particle swarm

optimization. In

Proceeding of the 1995 IEEE

International Conference on Neural Networks

, 4,

1942-1948. IEEE Press. Retrieved from: IEEE Xplore

Digital Library.

Kennedy, J. and Eberhart, R. 1997. A discrete binary

version of the particle swarm algorithm. In

Proceeding

of the 1997 IEEE International. Conference on

Systems, Man, and Cybernetics

, 5, 4104-4108. IEEE

Press. Retrieved from: IEEE Xplore Digital Library.

Knudsen, S. (2002).

A Biologist’s Guide to Analysis of

DNA Microarray Data

ed.). New York: John

Wiley & Sons.

Li, S., Wu, X. and Tan, M. (2008). Gene Selection Using

Hybrid Particle Swarm Optimization and Genetic

Algorithm.

Soft Computing, 12, 1039-1048.

doi:10.1007/s00500-007-0272-x

Mohamad, M. S., Omatu, S., Yoshioka, M. and Deris, S.

(2009). A Cyclic Hybrid Method to Select a Smaller

Subset of Informative Genes for Cancer Classification.

International Journal of Innovative Computing,

Information and Control

, 5(8), 2189-2202.

Shen, Q., Shi, W. M. and Kong, W. Hybrid Particle

Swarm Optimization and Tabu Search Approach for

Selecting Genes for Tumor Classification Using Gene

Expression Data.

Computational Biology and

Chemistry

, 32, 53-60. doi:10.1016/j.compbiolchem.

2007.10.001

SELECTING GENES FROM GENE EXPRESSION DATA BY USING AN ENHANCEMENT OF BINARY PARTICLE

SWARM OPTIMIZATION FOR CANCER CLASSIFICATION