A CONCEPTUAL STUDY OF MODEL SELECTION IN

CLASSIFICATION

Multiple Local Models vs One Global Model

R. Vilalta, F. Ocegueda-Hernandez and C. Bagaria

Department of Computer Science, University of Houston, 4800 Calhoun Rd., Houston TX 77204-3010, U.S.A.

Keywords:

Model selection, Classiﬁcation, Supervised learning, VC dimension.

Abstract:

A key concept in model selection is to understand how model complexity can be modiﬁed to improve in

generalization performance. One design alternative is to increase model complexity on a single global model

(by increasing the degree of a polynomial function); another alternative is to combine multiple local models

into a composite model. We provide a conceptual study that compares these two alternatives. Following the

Structural Risk Minimization framework, we derive bounds for the maximum number of local models or folds

below which the composite model remains at an advantage with respect to the single global model. Our results

can be instrumental in the design of learning algorithms displaying better control over model complexity.

1 INTRODUCTION

A classiﬁcation problem is commonly tackled by us-

ing a single global model over the whole attribute or

variable space, but a popular alternative is to com-

bine multiple local models to form a composite clas-

siﬁer. As an illustration, in learning how to effec-

tively classify stars according to temperature-inferred

spectral lines (e.g., O, B, A, etc.), one must ﬁrst

choose a family of models (e.g., discriminative lin-

ear or quadratic functions), followed by a search for

an optimum global model. A different solution is

to combine different local models, each model de-

signed for a speciﬁc classiﬁcation task. In the ex-

ample above, each class can be further decomposed

into a ﬁner classiﬁcation by attaching a digit (0-9) to

each spectrum letter that represents tenths of range

between two star classes. Local models can be trained

to learn each of the ten subclasses for each star letter-

type, later to be combined into a single composite

model.

In general, model selection in classiﬁcation deals

with the problem of choosing the right degree of

model complexity as dictated by the expected value of

model performance over the entire joint input-output

distribution (Kearns et al., 1997). Model complexity

increases when we choose a family of models char-

acterized by added ﬂexibility in the shape of the deci-

sion boundary; but complexity increases as well when

we combine several models of similar complexity into

a composite model (e.g. switching from discrimina-

tive linear functions to decision trees).

The problem we address is the following. Under

certain assumptions, when is it preferred to combine

multiple local models into one composite model, as

opposed to having a single global model? By a com-

posite model we mean a model that combines k deci-

sion boundaries or folds, as opposed to a single com-

plex decision boundary or fold. Our interpretation of

global and local models differs from a classical view,

where in computing class posterior probabilities we

can either employ all available training examples (i.e.,

global strategy) or give higher weight to those train-

ing examples in the neighborhood of the query exam-

ple (i.e., local strategy). In contrast we emphasize the

effect of combining multiple local models into a com-

posite model, and study the competitiveness of such

model.

Following the framework of Structural Risk Mini-

mization (SRM) and making use of the VC-dimension

(Vapnik, 1999), we provide a theoretical study that

explicitly indicates the maximum number k of folds

below which the composite model remains at an ad-

vantage with respect to the single model (based on

113

Vilalta R., Ocegueda-Hernandez F. and Bagaria C. (2010).

A CONCEPTUAL STUDY OF MODEL SELECTION IN CLASSIFICATION - Multiple Local Models vs One Global Model.

In Proceedings of the 2nd International Conference on Agents and Artiﬁcial Intelligence - Artiﬁcial Intelligence, pages 113-118

DOI: 10.5220/0002733601130118

 SciTePress

expected risk or loss, Section 3). This is important to

understand alternative approaches to model selection,

where instead of increasing the complexity of a sin-

gle model in long steps (e.g., by increasing the degree

of a polynomial), we can add ﬁner steps by combin-

ing equally-complex models. Our results show that

one can in principle add tenths of equally-complex

local models before attaining the same expected risk

equivalent to a single model; our basic assumption

is that the complex model has VC-dimension higher

than each local model.

Figure 1 shows a diagram illustrating our main

ideas. Traditional approaches to model selection vary

complexity by jumping between model families F

;

every single model in the new family is able to create

more ﬂexible decision boundaries compared to any

single model in the ﬁrst family. Alternatively, com-

plexity can vary by combining multiple models into

a composite model (while ﬁxing the complexity of

each single model in the ﬁrst family); every model in

the new family F

is the result of combining k mod-

els from the ﬁrst family F

. New models are also

more complex but due to the composite approach.

The question is how do these two approaches com-

pare? How much complexity is precisely increased

with each approach? When combining k models, how

far can k increase until complexity grows above the

traditional approach of invoking single complex mod-

els? By answering these questions we open the possi-

bility of including both approaches in the same model

selection strategy, while expanding our understanding

of learning-algorithm designs.

This paper is organized as follows. Section 2

provides preliminary information in classiﬁcation and

Structural Risk Minimization. Section 3 is a concep-

tual study that compares a composite model made of

multiple local models vs one single model. Finally,

section 4 gives a summary and discusses future work.

2 PRELIMINARIES

2.1 Basic Notation in Classiﬁcation

Let (A

, A

, ··· , A

) be an n-component vector-valued

random variable, where each A

represents an attribute

or feature; the space of all possible attribute vec-

tors is called the input space X . Let {y

, y

, ··· , y

}

be the possible classes, categories, or states of na-

ture; the space of all possible classes is called the

output space Y . A classiﬁer receives as input a set

of training examples T = {(x, y)}, |T | = N, where

x = (a

, a

, ··· , a

) is a vector or point in the in-

put space and y is a point in the output space. We

Figure 1: Two types of model selection. Top: Complexity is

increased by looking at families of models F

with increased

ﬂexibility in the decision boundaries. Bottom: Complexity

is increased by combining k models while ﬁxing the com-

plexity of each model. F

stands for the combination of k

models of family F

. If we could compare both approaches

–as in this example– we could say that model family F

less complex than family F

, which in turn is less complex

than family F

assume T consists of independently and identically

distributed (i.i.d.) examples obtained according to a

ﬁxed but unknown joint probability distribution in the

input-output space X ×Y . The outcome of the classi-

ﬁer is a function or model f mapping the input space

to the output space, f : X → Y . We consider the case

where a classiﬁer deﬁnes a discriminant function for

each class g

(x), j = 1, 2, ··· , k and chooses the class

corresponding to the discriminant function with high-

est value (ties are broken arbitrarily):

f (x) = y

iff g

(x) ≥ g

(x) (1)

We work with kernel methods (particularly support

vector machines), where a solution to the classiﬁca-

tion (or regression) problem uses a discriminant func-

tion of the form:

g(x) =

∑

i=1

K(x

, x) (2)

where {α

} is a set of real parameters, index i runs

along the number of training examples, and K is a

kernel function in a reproducing kernel Hilbert space

(Shawe-Taylor and Cristianini, 2004). We assume

polynomial kernels K(x

, x

) = (x

·x

)

, where p is

the degree of the polynomial.

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

114

3 A CONCEPTUAL STUDY

We now study the problem of model selection based

on the criterion proposed by Vapnik (Vapnik, 1999;

Hastie et al., 2001) under the name of Structural

Risk Minimization (SRM). Here the objective is

to minimize the expected value of a loss function

L(y, f (x)) that states how much penalty is assigned

when our class estimation f (x) differs from class y.

A typical loss function is the zero-one loss function

L(y, f (x)) = I(y 6= f (x)), where I(·) is an indicator

function. We deﬁne the risk in adopting a family of

models parameterized by θ as the expected loss:

R(θ) = E[L(y, f (x|θ))] (3)

which cannot be estimated precisely because y(x ) is

unknown. One can compute instead the empirical

risk:

R(θ) =

∑

i=1

L(y

, f (x

|θ)) (4)

where N is the size of the training set. Using a mea-

sure of model-family complexity h, known as the VC-

dimension (Vapnik, 1999), the idea is now to provide

an upper bound on the true risk using the empirical

risk and a function that penalizes for complex models

using the VC dimension:

SRM:

R(θ) ≤

R(θ) +

h(ln

+ 1) −ln(

)

(5)

where the inequality holds with probability at least

1−η over the choice of the training set. The goal is to

ﬁnd the family of models that minimizes equation 5.

The ideas just described are typical on model se-

lection techniques. Since our training set T comprises

a limited number of examples and we do not know

the form of the true target distribution, the problem

we face is referred to as the bias-variance dilemma

in statistical inference (Geman et al., 1992; Hastie

et al., 2001). Speciﬁcally, simple classiﬁers exhibit

limited ﬂexibility on their decision boundaries; their

small repertoire of functions produces high bias (since

the best approximating function may lie far from the

target function) but low variance (since there is lit-

tle dependence on local irregularities in the data). In

such cases, it is common to see high values for the

empirical risk but low values for the penalty term. On

the other hand, complex models encompass a large

class of approximating functions; they exhibit ﬂexi-

ble decision boundaries (low bias) but are sensitive to

small variations in the data (high variance). Here, in

contrast, we commonly ﬁnd low values for the em-

pirical risk but high values for the penalty term. The

goal in SRM is to minimize the right hand side of in-

equality 5 by ﬁnding a balance between empirical er-

ror and model complexity, where the VC dimension h

becomes a controllable variable.

3.1 Multiple Models vs One Model

We now provide an analysis of the conditions under

which combining multiple local models is expected

to be beneﬁcial. In essence we wish to compare a

composite model M

to a basic global model M

. M

is the combination of multiple models. We assume

has VC-dimension h

and M

has VC-dimension

, which comes from the combination of k models,

each of VC-dimension at most h, where we assume

h < h

The question we address is the following: how

many models of VC-dimension at most h can M

comprise to still improve on generalization accuracy

over M

, assuming both models have the same empir-

ical error? The question refers to the maximum value

of k that still gives an advantage of M

over M

. To

proceed we look at the VC-dimension of h

, which in

essence is the VC-dimension of k-fold unions or inter-

sections. It is an open problem to determine the VC-

dimension of a family of k-fold unions (Reyzin, 2006;

Blumer et al., 1989; Eisenstat and Angluin, 2007); re-

cent work, however, shows that such a family of mod-

els has a lower bound of

kh, and an upper bound of

2kh log

3k (it has been shown that O(nk log

k) is a

tight bound (Eisenstat and Angluin, 2007)). We be-

gin our study with the lower optimistic bound, and

assume the VC-dimension of h

to be

kh. To solve

the question above we equate the right hand side in

equation 5 for both M

and M



+ 1



−ln(

)



+ 1



−ln(

)

(6)

where our goal is now simply to solve for k. After

some algebraic manipulation we get the following:

k −k ln k = c

(7)

where c

and c

are constants:

= ln2N + 1 −ln(

h) (8)

A CONCEPTUAL STUDY OF MODEL SELECTION IN CLASSIFICATION - Multiple Local Models vs One Global

Model

115

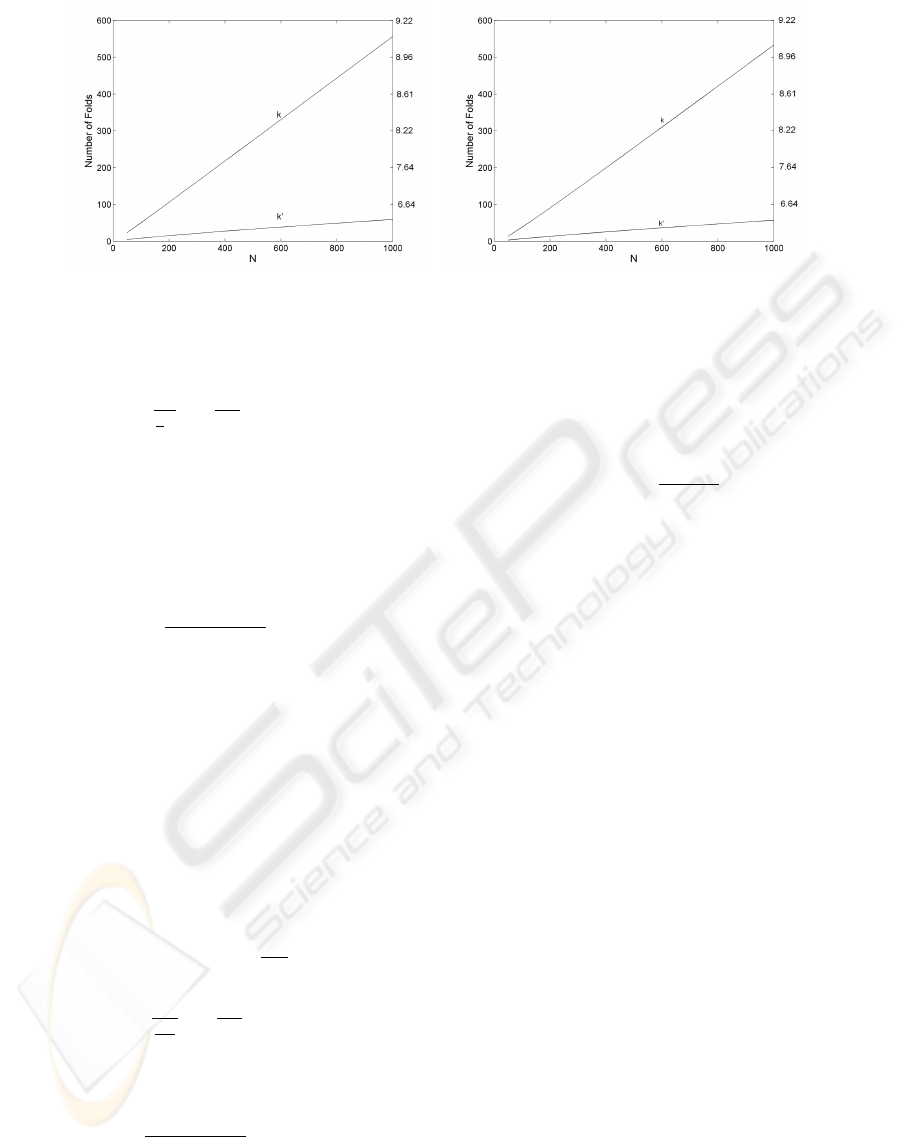
Figure 2: Left: A comparison of a compound model using k (k

) support vector machines with polynomial kernels of degree

one vs a simple support vector machine with a polynomial kernel of degree two; Right: same comparison except the simple

support vector machine has a polynomial kernel of degree four. The degree of the polynomial kernel makes little difference

in the results.



+ 1



(9)

Equation 7 can be formulated as a transcendental al-

gebraic equation. We can transform the equation as

follows:

−c

−1

−c

−1

= −c

−c

(10)

To solve for k we can use Lambert’s W function:

k =

−c

W (−c

−c

)

(11)

where W can be solved using a numeric approxima-

tion.

A similar analysis can be done using the upper

bound of h

= 2k

hlog

, where we use k

to dif-

ferentiate from the k used with the lower bound. Af-

ter some algebraic manipulation we get the following

equation:

ν −ν ln ν = c

(12)

where ν = k

ln3k

, and c

and c

are constants (only

slightly different than before):

= ln2N + 1 −ln(

ln2

) (13)

ln2



+ 1



(14)

Since equations 7 and 12 have the same form, ν has

the same solution as k (equation 11):

ν =

−c

W (−c

−c

)

= c

(15)

We can then do the substitution back to k

to obtain

the following:

ln3k

= c

(16)

)

−1

)

−1

= 3c

(17)

It is now possible to solve for k

W (3c

)

(18)

To summarize, we have shown how to express the

number of k-fold (and k

-fold) unions of models, each

with VC-dimension h, such that the resulting com-

pound model exhibits the same guaranteed risk as

a single model with VC-dimension h

(we assume

of course that h < h

). To clarify, we handle two

bounds, k and k

, because of our uncertainty in the

VC-dimension of model unions. In principle we know

there is a k

, that stands as the exact bound, below

which M

retains an advantage over M

We can now study the effect on k (and k

) as we

vary parameters such as the size of the training set,

or the VC-dimension of the models in the compos-

ite model M

(as compared to the global model M

Figures 2 and 3 show plots on how the number of

model unions varies with different values of N. In

each case we take the compound model as the union

of k (and k

) support vector machines, where the sim-

ple global model is a single support vector machine.

We assume the use of polynomial kernels where the

VC-dimension of each model is deﬁned as (Burges,

1998):

h =



n + p −1



+ 1 (19)

where n is the dimensionality of the input space and

p is the degree of the polynomial. In Figure 2 we as-

sume a compound model with polynomial kernels of

degree p = 1. The global model varies from a poly-

nomial degree p = 2 (Figure 2-left) to a polynomial

degree p = 4 (Figure 2-right). In all cases we as-

sume n = 5. It is clearly observed that the value of

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

116

Figure 3: Left: A comparison of a compound model using k (k

) support vector machines with polynomial kernels of degree

two vs a simple support vector machine with a polynomial kernel of degree three; Right: same comparison except the simple

support vector machine has a polynomial kernel of degree ﬁve. The degree of the polynomial kernel makes little difference in

the results.

k (k

) increases linearly with N. As expected, k

cor-

responds to a less inclined line as the upper bound on

the VC-dimension lowers the number of models we

can place at the composite model while still gener-

ating less variance as the single model. In addition,

a higher difference in VC-dimension (Figure 2-right)

shows almost no difference in the shape of k (k

) for

different values of N. The right y-axis on each graph

is the log

of the values on the left y-axis; it is sim-

ply an indicator of how many local models we could

arrange in a hierarchical structure (assuming a binary

tree) while still generating less variance as the global

model. We observe that for large values of N (e.g.,

N > 500), large hierarchies can be employed with lit-

tle effect over the variance component.

Figure 3 assumes a compound model with poly-

nomial kernels of degree p = 2. The single model

varies from a polynomial degree p = 3 (Figure 3-

left) to a polynomial degree p = 5 (Figure 3-right).

The same effect is observed as before except under

a different scale. In all graphs we observe a large

advantage gained by the combination of many low-

complex models as compared to a single model ex-

hibiting higher complexity. The difference grows lin-

early on N and is considerable for N > 500.

Until now we have assumed the empirical error to

be the same for the compound model M

and for the

global model M

. We now analyze the case where

empirical errors differ. Let

(θ) be the empirical

error for M

and

(θ) the corresponding error for

; we deﬁne the difference in empirical error as

∆

R(θ) =

(θ) −

(θ), and ask the same question as

before, how many models of VC-dimension at most

h can M

comprise to still improve on generalization

accuracy over M

? This time, however, we account

for differences in empirical error. Our previous anal-

ysis remains almost the same. We need only make a

modiﬁcation on two constants:



+ 1



−2

√

N∆

R(θ)Ψ + N∆

R(θ)

(20)



+ 1



−2

√

N∆

R(θ)Ψ + N∆

R(θ)

ln2

(21)

where

Ψ =

+ 1 −ln(

) (22)

Figure 4 shows plots on how the number of model

unions varies with different values of ∆

R(θ) when

N = 500 and the conﬁdence level is set to η = 0.05.

Here we assume a compound model with polynomial

kernels of degree p = 1 and a global model with a

polynomial kernel of degree p = 2. Figure 4-left

shows the case when n = 5 and Figure 4-right shows

the case when n = 15. Surprisingly, error differences

have little effect on the value of the number of folds.

We also observe that an increase in the dimensional-

ity of the space imposes a tighter bound on the num-

ber of combined models (it adds weight to the VC-

dimension of every model).

Overall we conclude that adding complexity to a

single model is equivalent to making long steps in

increasing model variability (as determined by the

penalty term in equation 5). Smaller steps can be

achieved through the union of simple models. Even

when it is known that the bounds derived from the

principle of SRM are not tight, the number of sim-

ple models that can be combined before reaching the

equivalent effect of a single but more complex model

is signiﬁcantly large.

A CONCEPTUAL STUDY OF MODEL SELECTION IN CLASSIFICATION - Multiple Local Models vs One Global

Model

117

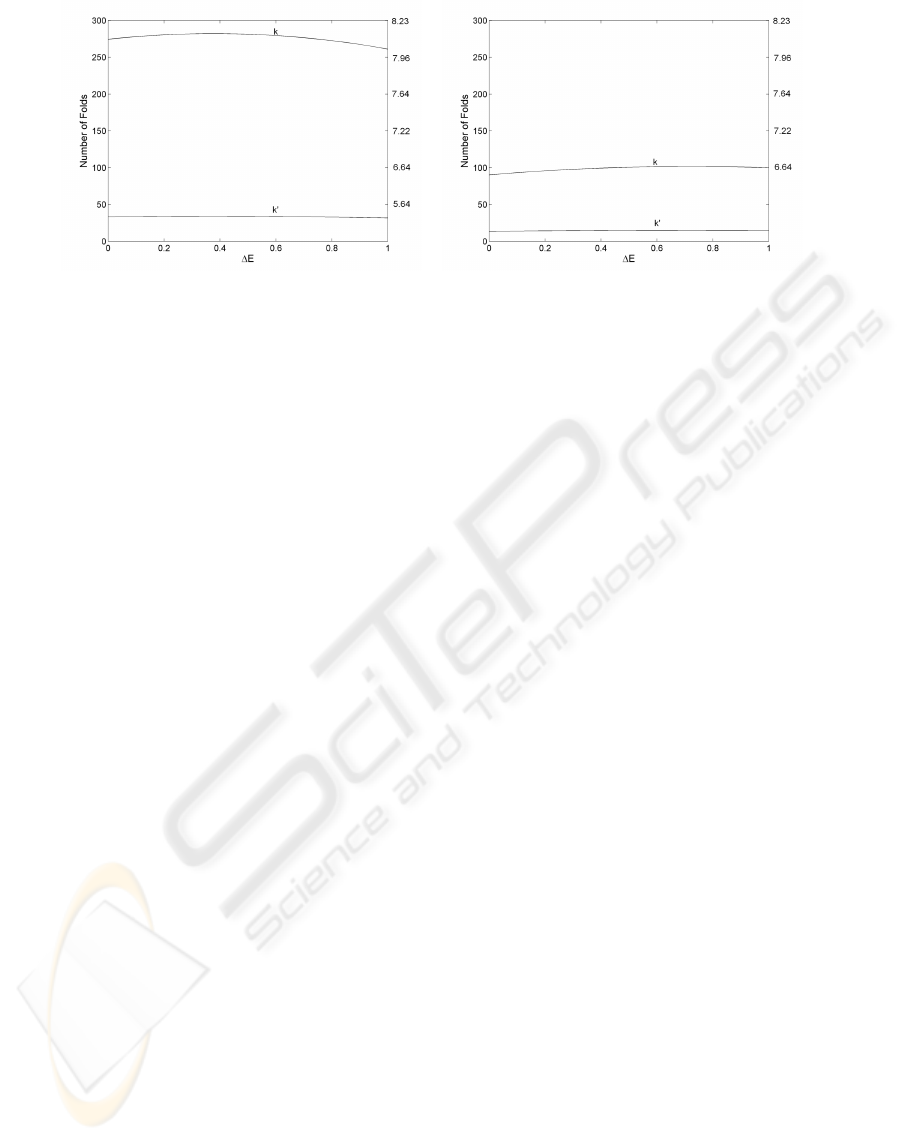
Figure 4: A comparison of a compound model using k (k

) support vector machines with polynomial kernels of degree one

vs a simple support vector machine with a polynomial kernel of degree two. The x-axis refers to the difference in empirical

error, ∆E = ∆

R(θ) =

(θ) −

(θ), between the compound model and the global model. Left: number of dimensions n = 5.

Right: number of dimensions n = 15.

4 SUMMARY AND FUTURE

WORK

Our study compares the bias-variance tradeoff of a

model that combines several simple classiﬁers with

a single more complex classiﬁer. Using standard

bounds for the actual risk (using the VC-dimension),

a single increase in the polynomial degree of the ker-

nel function for a support vector machine increases

the variance component signiﬁcantly. As a result,

multiple simple classiﬁers can be combined before

the compound model exceeds the variance of a sin-

gle more complex classiﬁer.

Our study advocates a piece-wise model ﬁtting ap-

proach to classiﬁcation, justiﬁed by the difference in

the rate of complexity obtained by augmenting the

number of boundaries per class (composite model)

to the increase in complexity obtained by augment-

ing the capacity of a single global learning algorithm

(classical approach). The former enables us to in-

crease the model complexity in ﬁner steps.

As future work we plan on extending our study to

hierarchical learning, where a data structure deﬁned a

priori over the application domain explicitly indicates

how classes divide into more speciﬁc sub-classes. A

hierarchical classiﬁcation model can be seen as the

composition of many models, one for each node in

the hierarchy. Our study can be used to compare hier-

archical models with single global models by taking

into account the increase in variance gained by reduc-

ing the size of the training set as each lower hierarchi-

cal node covers a smaller number of examples.

ACKNOWLEDGEMENTS

This work was supported by National Science Foun-

dation under grants IIS-0812372 and IIS-0448542,

and by the Army Research Ofﬁce under grant

56268NSII. F. Ocegueda-Hernandez was supported

by CONACyT (Mexico), Ph.D. fellowship 171936.

REFERENCES

Blumer, A., Ehrenfeucht, A., Haussler, D., and Warmuth,

M. (1989). Learnability and the vapnik-chervonenkis

dimension. Journal of the ACM, 36(4):929–965.

Burges, C. J. C. (1998). A tutorial on support vector

machines for pattern recognition. Data Mining and

Knowledge Discovery, 2(2):121–167.

Eisenstat, D. and Angluin, D. (2007). The vc dimen-

sion of k-fold union. Information Processing Letters,

101(5):181–184.

Geman, S., Bienenstock, E., and Doursat, R. (1992). Neu-

ral networks and the bias/variance dilemma. Neural

Computation, 4(1):1–58.

Hastie, T., Tibshirani, R., and Friedman, J. (2001). The Ele-

ments of Statistical Learning: Data Mining, Inference,

and Prediction. Springer.

Kearns, M., Mansour, Y., Ng, A., and Ron, D. (1997). An

experimental and theoretical comparison of model se-

lection methods. Machine Learning, 27(1):7–50.

Reyzin, L. (2006). Lower bounds on the vc dimen-

sion of unions of concept classes. Technical Re-

port, Yale University, Department of Computer Sci-

ence, YALEU/DCS/TR-1349.

Shawe-Taylor, J. and Cristianini, N. (2004). Kernel Meth-

ods for Pattern Analysis. Cambridge University Press.

Vapnik, V. (1999). The Nature of Statistical Learning The-

ory. Springer, 2nd edition.

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

118