EXTRACTING CASE-BASED ANSWERS FROM
CLOSED PROOF-TREES
Isabel Gomes Barbosa and Newton Jos´e Vieira
Universidade Federal de Minas Gerais, Belo Horizonte, Minas Gerais, Brazil
Keywords:
First-order logic, Disjunctive answers, Case-based answers, Proof-trees.
Abstract:
A question of the form “Find X such that P(X) is true” may produce in the most usual inference systems an
answer that has the general form P(T
1
) ∨ P(T
2
) ∨ ... ∨ P(T
k
). If we have k ≥ 2, the answer is then termed a
disjunctive answer. In some scenarios, a disjunctive answer of this form may be considered too imprecise to
help the user in his activities. However, an answer which specifies the cases in which each element P(T
i
) is
true would be a perfectly appropriate answer to the question. In this paper, we propose an algorithm that, from
a deduction of P(T
1
) ∨ P(T
2
) ∨ ...∨ P(T
k
), k ≥ 2, on the form of a proof-tree, extracts a case-based answer to
the exact same question. A case-based answer is an answer given in terms of a finite number of cases, each
one implying a non-disjunctive answer P(T
i
),1≤ i ≤ k, to the user’s question.
1 INTRODUCTION
Given a knowledge base represented in a first-order
language, a question of the form
Find X such that P(X) is true,
may produce in the most usual inference systems an
answer of the form
P(T
1
) ∨ P(T
2
) ∨ ...∨ P(T
k
),
where each T
i
is an n-tuple of ground terms (Green,
1969).
If we have k ≥ 2, the answer is then termed a dis-
junctive answer. A disjunctive answer presents dif-
ferent possible answers to the question, at least one
of which is true. Disjunctive answers are considered
less informative than non-disjunctive answers, since
they inform that the disjunction as a whole is true, but
do not specify which elements of the disjunction are
indeed correct answers to the question. This lack of
information induces uncertainty in the answer. One
way to reduce this uncertainty is to analyze the dis-
junctive answer by an exhaustive set of cases in the
problem domain. I.e., we can split the problem into
several (exhaustive) cases, where each case implies
a non-disjunctive answer P(T
i
),1≤ i ≤ k. Cases
α
1
, α
2
,...,α
m
are exhaustive if α
1
∨α
2
∨...∨α
m
is a
logical consequence of the knowledge base. An incip-
ient way to achieve this is shown in (Chang and Lee,
1997) in the context of resolution refutation.
As an example, adapted from (Chang and Lee,
1997), consider a knowledge base defined by the
clauses below:
(1) adult(John) ∨ prescribe(John,a)
(2) ¬adult(John) ∨ prescribe(John,b)
and the question “What drug should be pre-
scribed to John?”, which logical form is “∃y
prescribe(John,y)”. In most inference systems, the
answer provided to this question would be the dis-
junctive answer
prescribe(John,a) ∨ prescribe(John,b).
From this answer, we cannot tell which drug, a or
b, should be prescribed to John. However, if instead
were returned as an answer
¬adult(John) → prescribe(John,a)
adult(John) → prescribe(John,b)
and the user knew whether John is an adult or not,
then he would determine the drug to be prescribed to
John. Note that in this example only two cases are
considered: the case in which John is an adult and the
case in which John is not.
The deduction of an answer carries with it infor-
mation about the question, many of which are not
available to users. Proof-trees (Vieira, 1987) are tree-
like structures that can be used to represent the his-
tory of a proof. In this work, we consider the rep-
resentation of proofs by proof-trees, like that used
377
Gomes Barbosa I. and José Vieira N. (2010).
EXTRACTING CASE-BASED ANSWERS FROM CLOSED PROOF-TREES.
In Proceedings of the 2nd International Conference on Agents and Artificial Intelligence - Artificial Intelligence, pages 377-384
DOI: 10.5220/0002736703770384
Copyright
c
 SciTePress

in Prolog implementations (Bruynooghe,1982), how-
ever our notion of proof-trees is extended to make it
complete for full first-order logic, in a way similar to
that proposed in MESON system by Loveland(1978).
The representation of a proof by proof-trees induces
the reading of clauses as implications, allowing an-
swer explanations independent of the steps actually
done by the inference system (Vieira, 1987).
Thus, in this paper, we present an algorithm that,
from a proof-tree that corresponds to a disjunctive an-
swer of the form
P(T
1
) ∨ P(T
2
) ∨ ...∨ P(T
k
),
k ≥ 2, extracts a case-based answer, of the form
α
1
→ P(T
i
1
)
α
2
→ P(T
i
2
)
...
α
m
→ P(T
i
m
)
1 ≤ i
1
, i
2
,...,i
m
≤ k, where α
1
∨ α
2
∨ ... ∨ α
m
is a
logical consequence of the knowledge base and α
j
is a case that implies the answer P(T
i
j
). Moreover,
we assume that each T
i
is a n-tuple of ground terms,
and so the answer is a “specific answer” according to
the classification of Burhans and Shapiro (2007). As
far as we know, the presentation of a specific disjunc-
tive answer in the above format is original. We are
still working in the generalization of our method to
the other classes of answers (generic and hypothetical
answers).
We must, however, emphasize that the quality of
the answers of our algorithm depends on the knowl-
edge present in the proof-tree. In particular, if the
knowledge is intrinsically disjunctive, then it may
not be possible to obtain an answer that has the
general form indicated above. For example, if you
ask the question “What subject does John teach?”,
and the knowledge base contains the fact that “John
teaches Mathematics or John teaches Logic”, then
from this fact it follows immediately the statement
“John teaches some subject.”. Obviously, a corre-
sponding proof-tree does not contain information that
would allows us to extract or construct cases that im-
ply the answer “John teaches Mathematics” or “John
teaches Logic”. Even if the proof-free has sufficient
knowledge for the extraction of an answer with the
above format, a meaningful answer could depend on
characteristics of the user not present in a proof-tree
(typically, one would try to capture such characteris-
tics in an user model). Any way, the non deterministic
algorithm to be presented will not exclude any of the
meaningful answers.
This work builds one additional step in the di-
rection of making formal methods of reasoning more
amenable to use in practice. It exhibits information
already present in a proof but otherwise concealed
from users. As a consequence, it makes a question-
answering system more “collaborative” at practically
no additional cost.
This paper is organized in the following way: sec-
tion 2 presents the definition of proof-trees and its
properties. Section 3 makes a brief discussion about
information extraction from closed proof-trees and
introduces an example that will be used to explain
the algorithm proposed. The algorithm for extract-
ing case-based answers from closed proof-trees is de-
scribed in section 4. Finally, the conclusions of this
work are presented in section 5.
2 PROOF-TREES
A proof-tree is essentially what in (Letz and Stenz,
2001) is defined as a clausal tableau. Proof-trees have
its nodes labeled with literals. In our definition of
proof-trees, we will use a linear notation. A proof-
tree is an ordered pair Lα, such that L is a literal and α
is a set (possibly empty) of literals and/or proof-trees.
The literals M of every subtree Mβ that occurs in Lα
are termed expanded literals. The remaining literals
are divided into two groups: reduced and candidate
literals. Candidate literals are literals that have yet to
be proven. Expanded and reduced literals are literals
already used in some inference rule of the proof pro-
cedure.
A proof-tree is defined inductively by the follow-
ing inference rules. The notation
L is used to refer to
the complement of literal L, while |L| is used to refer
to the atom of literal L.
(Codification rule) The codification of an input
clause L
1
∨ L
2
∨ ... ∨ L
m
produces the proof-tree
⊥{
L
1
, L
2
,...,L
m
}. Thus, the root of every proof-
tree is the literal ⊥ (falsum).
(Expansion rule) The expansion of a proof-tree
⊥{...L
1
...}, where L
1
is a candidate literal,
with an input clause M
0
∨ M
1
∨ ... ∨ M
n
such
that L
1
and M
0
are unifiable with most gen-
eral unifier (mgu) σ, produces the proof-tree
⊥{...L
1
{M
1
, M
2
,...,M
n
}...}σ.
(Reduction rule) The reduction of a proof-tree
⊥{...L
1
{...L
2
...}...}, where L
2
is a candidate
literal of opposite sign to L
1
and |L
1
| and |L
2
|
are unifiable with mgu σ, produces the proof-tree
⊥{...L
1
{...L
2
...} ...}σ.
Every deduction starts with the application of the cod-
ification rule, which produces the initial proof-tree.
The expansion and reduction rules are similar to the
extension and reduction rules of model elimination
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
378

(Loveland, 1969). Expanded and candidate literals
are termed A-literals and B-literals in model elimi-
nation proof procedures. The structure provided by
proof-trees is similar to that proposed by the MESON
system of Loveland (1978).
A proof-tree without candidate literals is called a
closed proof-tree. A finite set of clauses S is unsatis-
fiable iff there exists a closed proof-tree for S (Vieira,
1987). Thus, we can prove by contradictionthat a for-
mula is a logical consequence of a set of hypotheses,
assuming, along with the hypothesis, the negation of
the formula and obtaininga closed proof-tree from the
resulting set.
Example 1. Consider the set of clauses S1:
1. P(x) ∨ R(x) ∨Q(x, y)
2. ¬Q(x, y) ∨ S(x)
3. ¬S(x) ∨¬Q(x, b)
4. ¬R(a)
and the question “S1 |= ∃xP(x)?”. Negating and pro-
ducing clauses:
5. ¬P(x)
From 1 to 5 we generate the following refutation:
6. ⊥{P(x)} (cod 5)
7. ⊥{P(x){¬R(x), ¬Q(x, y)}} (exp 1)
8. ⊥{P(a){¬R(a){}, ¬Q(a, y)}} (exp 4)
9. ⊥{P(a){¬R(a){}, ¬Q(a, y){¬S(a)}}} (exp 2)
10. ⊥{P(a){¬R(a){}, ¬Q(a,
y){¬S(a){Q(a, b)}}}}
(exp 3)
11. ⊥{P(a){¬R(a){}, ¬Q(a, b){¬S(a){Q(a, b)}}}}
(red)
The closed proof-tree 11 is represented graphi-
cally in Fig. 1.
⊥
P(a)
(5)
¬R(a)
(4)
¬Q(a, b)
(1)
¬S(a)
(2)
Q(a, b)
(3)
Figure 1: A closed proof-tree generated from the clauses
1-5.
Note that a proof-tree makes explicit a set of
clause instances in the form of implications. For ex-
ample, the proof-tree in Fig. 1 shows the following
instances:
P(a) →⊥ (clause 5)
¬R(a)(clause 4)
¬R(a) ∧¬Q(a, b) →P(a)(clause 1)
¬S(a) →¬Q(a, b)(clause 2)
Q(a, b) →¬S(a)(clause 3)
One can transform a proof-tree into an equivalent
proof-treewhere the codified clause is any clause used
in expansions. Both trees are equivalent in the sense
that they result from diferent proofs of the same the-
orem and lead to the same answer; more precisely, in
terms of the Herbrand theorem, the set of insatisfiable
instances is the same in both cases. That transforma-
tion, explained in (Vieira, 1987), is based on the fact
that the formula
L
1
∧ ...∧ L
n
→ M
is logically equivalent to n formulas
L
1
∧ ...∧ L
i−1
∧ L
i+1
∧ ...∧ L
n
∧ M → L
i
,
obtained by complementingand interchangingthe lit-
eral M with each literal L
i
in turn, and to the formula
L
1
∧ ...∧ L
n
∧ M →⊥.
Using these equivalences,the proof-tree of the last ex-
ample could be transformed in order that the clause 2
appears as the codified clause, as shown in Fig. 2.
⊥
Q(a, b)
¬P(a)
(5)
¬R(a)
(4)
(1)
¬S(a)
(2)
Q(a, b)
(3)
¬P(a)
(5)
¬R(a)
(4)
(1)
Figure 2: A proof-tree equivalent to that of Fig. 1.
In the next section we show how an answer can be
extracted from a proof-tree.
3 ANSWER EXTRACTION
In this section we explain how disjunctive answers are
extracted from a proof-tree. Afterward, in the next
EXTRACTING CASE-BASED ANSWERS FROM CLOSED PROOF-TREES
379

section, we will show how to extract cases that justify
each disjunct.
After a proof is found, we can extract values
for the existentially quantified variables of the for-
mula associated to the question from the instances of
clauses of the negated question, ¬P(X), that appears
on the proof-tree. The questions considered in this
work are those which result in disjunctive answers of
the form P(T
1
) ∨P(T
2
) ∨... ∨ P(T
k
), k ≥ 2. In proof-
trees, disjunctive answers are caused by expansions
with clauses derived from the negation of the ques-
tion. Each instance of clause from the negation of the
question that appears in the proof-tree gives us an el-
ement of the disjunction (Vieira, 1987).
The algorithm for extracting case-based answers
will be applicable only when the question is repre-
sented by an atomic formula. This assumption does
not restrict generality. If the question is a general for-
mula
F (X), we add the clausal form of ∀X (F (X) →
→ Q(X)) to the knowledge base, where Q isanew
predicate symbol, and the question is represented by
the positive literal Q(X). This strategy is followed
in several works such as, for example, (Demolombe,
1992) and (Burhans and Shapiro, 2007).
Next, we present an example that will be used to
demonstrate the application of the algorithm.
Example 2. Suppose a knowledge base that contains
the following set of clauses, where Q(x, n) means that
x can borrow n books:
1. Stud(x) ∨ Staf(x) ∨ Vis(x)
Students, staff and visitors are eligible to borrow books
2. ¬Stud(x) ∨ Und(x) ∨ Grad(x)
Students are divided into under and graduate students
3. ¬Stud(x) ∨¬Und(x) ∨ Q(x,4)
Undergraduate students can borrow 4 books
4. ¬Stud(x) ∨¬Grad(x) ∨ Q(x,8)
Graduate students can borrow 8 books
5. ¬Sta f(x) ∨ Acad(x) ∨ Adm(x)
The staff is divided into academic and administrative
6. ¬Sta f(x) ∨¬Acad(x) ∨ Q(x,8)
The academic staff can borrow 8 books
7. ¬Sta f(x) ∨¬Adm(x) ∨ Q(x,2)
The administrative staff can borrow 2 books
8. ¬Vis(x) ∨ Q(x,4)
Visitors can borrow 4 books
9. ¬Und(J) John is not an undergraduate
And the question “How many books can John bor-
row?”, formulated as “Find y such that Q(J,y)”. The
clause from the negation of the question is:
10. ¬Q(J,y)
In Fig. 3, a closed proof-tree is given. From this
proof-tree, we obtain the answer:
⊥
Q(J,4)
(10)
Vis(J)
(8)
¬Stud(J)
¬Und(J)
(9)
¬Grad(J)
(2)
Stud(J) ¬Q(J,8)
(10)
(4)
¬Sta f (J)
(1)
Acad(J)
Sta f (J) ¬Adm(J)
(5)
Sta f (J) ¬Q(J,2)
(10)
(7)
¬Q(J,8)
(10)
(6)
Figure 3: Proof-tree T
0
for Example 2.
Q(J,2) ∨ Q(J,4) ∨ Q(J,8).
This answer has the general form:
P(T
1
) ∨ P(T
2
) ∨ ...∨ P(T
k
), k ≥ 2.
The next section describes the algorithm for extract-
ing cased-based answers from closed proof-trees and
applies it to the proof-tree illustrated in Fig. 3.
4 ALGORITHM FOR
CASE-BASED ANSWERS
EXTRACTION
The algorithm begins from the deduction of
P(T
1
) ∨ P(T
2
) ∨ ...∨ P(T
k
), k ≥ 2, on the form of a
proof-tree. We shall denote this proof-tree by
T
0
. The
algorithm is divided into six steps, where each step
has as input a tree
T
i
. The trees T
0
and T
1
are simply
proof-trees. The other trees generated by the algo-
rithm will be called answer-trees. The general pur-
pose of the algorithm is to transform the initial proof-
tree
T
0
into a final answer-tree T
5
, which corresponds
to a case-based answer. Thus, from
T
5
, we can di-
rectly extract a cased-based answer to the user’s ques-
tion. Firstly, we define the notion of a tree
T
i
in the
context of the algorithm.
Definition 1. Let Σ be a set of literals. A tree
T
i
over
Σ is a 4-tuple (N, A, λ, r), where:
• N is a finite set of nodes;
• A ⊆ (N × N) is a set of arcs;
• λ is a function assigning a label to each node:
λ : N → C, where C is the set of (finite) conjunc-
tions of literals from Σ. Usually, λ assigns a single
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
380

literal to a node. In the tree T
0
, shown in Fig. 3,
λ(v) is the literal that appears inside each box;
• r ∈ N is the root.
Def. 1 applies to both proof-trees and answer-
trees, as they have exactly the same structure, though
different readings.
Let Q be the predicate symbol of the question lit-
eral. If for all nodes v of tree
T
0
, except its root,
λ(v) has Q as its predicate symbol, then the algorithm
does not apply: the knowledge used is intrinsically
disjunctive. An example is: if the knowledge base
contains Q(a)∨ Q(b) and the question is “Find x such
that Q(x)”, an answer is Q(a)∨Q(b); there is no case-
based answer.
Next, we describe the six steps of the algorithm.
Each step is exemplified using the knowledge base
and question from Example 2. The proof of correcte-
ness of the algorithm is not presented here due to the
limit on the number of pages.
Step 1. Transform
T
0
into an equivalent (i.e., having
the same instances) proof-tree
T
1
, where each node
v of
T
1
such that λ(v) has Q as its predicate symbol
is a leaf. In doing this, choose as the codified clause
of
T
1
(a) a clause without any literal having Q as its
predicate symbol or (b) a tautological clause of the
form L∨
L, where L is a literal that doesn’t have Q as
its predicate symbol. The option (b) is the only option
for the simple example seen in the Introduction. Fig.
4 shows
T
0
and T
1
for that example.
⊥
prescribe(John, a)
(3)
¬adult(John)
(1)
¬prescribe(John, b)
(3)
(2)
⊥
¬adult(John)
¬prescribe(John, b)
(3)
(2)
adult(John)
(tautology)
¬prescribe(John, a)
(3)
(1)
Figure 4: Trees T
0
and T
1
for the Introduction’s example.
In the example of the previous section, the clause
from the negation of the question is 10, which is the
codified clause of Fig. 3. Taking the option (a),
clauses 1, 2 or 5 can be chosen as the codified clause,
because they don’t have a literal with Q as predicate
symbol. We transform the proof-tree
T
0
of Fig. 3
into the equivalent proof-tree shown in Fig. 5, where
clause 1 appears as the codified clause. Every literal
in
T
1
that were expanded by the clause derived from
the negated question is termed a negated question-
literal. In Fig. 5, such literals are shown inside the
rectangles filled with color gray. Note that every
negated question-literal in Fig. 5 is labeling a leaf
node.
⊥
¬Stud(J)
¬Und(J)
(9)
¬Grad(J)
(2)
Stud(J) ¬Q(J,8)
(10)
(4)
¬Sta f (J)
Acad(J)
Sta f (J) ¬Adm(J)
(5)
Sta f (J) ¬Q(J,2)
(10)
(7)
¬Q(J,8)
(10)
(6)
¬Vis(J)
(1)
¬Q(J,4)
(10)
(8)
Figure 5: Proof-tree T
1
for Example 2.
Step 2. Let T
1
=(N, A, λ
1
, r) be the proof-tree ob-
tained in Step 1. From
T
1
, we now obtain the answer-
tree
T
2
=(N, A, λ
2
, r), where:
λ
2
(v)=λ
1
(v), for every v ∈ N.
For our example,
T
2
is shown in Fig. 6.

Stud(J)
Und(J) Grad(J)
¬Stud(J) Q(J,8)
Sta f (J)
¬Acad(J)
¬Sta f (J) Adm(J)
¬Sta f (J) Q(J,2)
Q(J,8)
Vis(J)
Q(J,4)
Figure 6: Answer-tree T
2
.
The status of each literal (expanded or reduced)
is preserved in an answer-tree. Also, if L is a negated
question-literal labeling a node v in the proof-tree, the
complementary literal,
L, that labels v in the answer-
tree, is a question-literal.
The set of represented implications are reversed in
such a way that
L
1
∧ ...∧ L
n
→ M
EXTRACTING CASE-BASED ANSWERS FROM CLOSED PROOF-TREES
381

becomes
M → L
1
∨ ...∨ L
n
in the answer-tree. Thus, if v ∈ N is an internal node
in
T
2
, and u
1
,...,u
m
∈ N are its child nodes, then the
following implication is an instance of a clause of the
knowledge base:
λ
2
(v) → λ
2
(u
1
) ∨ ...∨ λ
2
(u
m
).
Step 3. Let
T
2
=(N, A, λ, r). For each non leaf node
v ∈ N, let
P(v) be the set of all its ancestors
1
a such
that there is a leaf b satisfying the conditions:
1. v is an ancestor of b;
2. λ(b) is a reduced literal;
3. λ(b) =
λ(a).
For a node v ancestor of a question-literal, if
a ∈
P(v), then the node a must be an ancestor of v in
any posterior answer-tree generated from
T
2
, in order
to obtain a correct final answer-tree. Fig. 7 shows the
set
P(v) next to each v, in the cases where P(v) =
/
0,
for the answer-tree of Fig. 6 (note the use of names A
and B for the first two sons of the root).

Stud(J) A
Und(J) {A} Grad(J)
¬Stud(J) Q(J,8)
Sta f (J) B
{B} ¬Acad(J)
¬Sta f (J) {B} Adm(J)
¬Sta f (J) Q(J,2)
Q(J,8)
Vis(J)
Q(J,4)
Figure 7: Answer-tree T
2
annotated with P(v).
Step 4. For answer-tree T
2
, we now delete every node
(and its associated arcs) which is not an ancestor of a
question-literal. The resulting answer-tree will be
T
3
as shown in Fig. 8.
2
As consequence of this step,
we have that every leaf in the resulting answer-tree
corresponds to a question-literal.
In answer-tree
T
3
=(N, A, λ, r), for an internal
node v ∈ N, denote by C(v) the conjunction of all lit-
erals λ(a) such that a ∈
P(v). Let u
1
,...,u
m
∈ N be
the child nodes of v. Then, we have that
C(v) ∧ λ(v) → λ(u
1
) ∨ ...∨ λ(u
m
)
follows from the knowledge base.
1
In this paper, the ancestors of a node v are all the nodes
along the path from the root to v not including v itself.
2
Node names D, E and F will be used in the next step.

Stud(J) A
{A} Grad(J) D
Q(J,8)
Sta f (J) B
{B} ¬Acad(J) E
{B} Adm(J) F
Q(J,2)
Q(J,8)
Vis(J)
Q(J,4)
Figure 8: Answer-tree T
3
.
Step 5. In answer-tree T
3
=(N, A, λ, r), let v, u ∈ N
be such that u is the only child of v, v = r and u is
not a leaf. Then one of them can be deleted from the
answer-tree if it is not a member of
P(a) for any of its
descendants a.Ifv is deleted, the father of v becomes
the father of u, and if u is deleted, its sons become
sons of v. Repeat the process for the resulting tree
until you obtain an answer-tree
T
4
, where every node,
except possibly the root, ramifies into two or more
branches or has a question-literal as its only child.
In Fig. 8, node D is the only child of A. Since A ∈
P(D), A can’t be deleted. Fig. 9 shows the answer-
tree
T
3.1
that results after deleting node D from T
3
.

Stud(J) A
Q(J,8)
Sta f (J) B
[B] ¬Acad(J) E
[B] Adm(J) F
Q(J,2)
Q(J,8)
Vis(J)
Q(J,4)
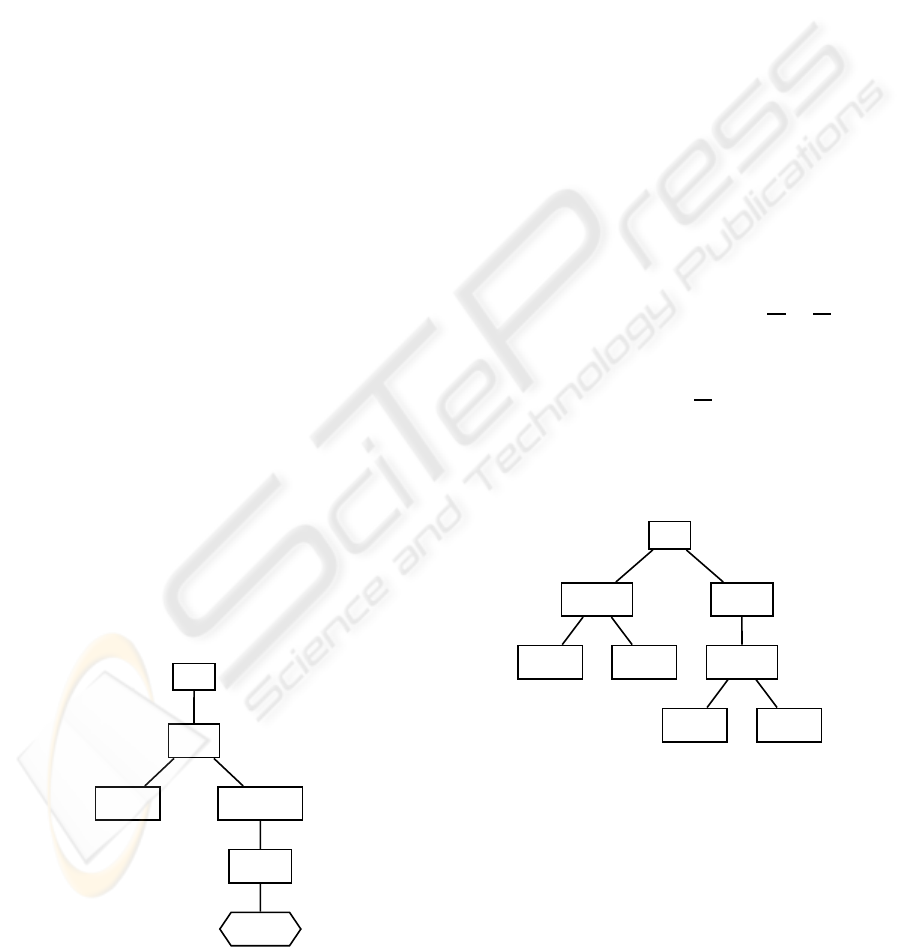
Figure 9: Answer-tree T
3.1
.
In Fig. 9, we still have that node F is the only
child of node E. Since E does not belong to the set
P(v), for any node v descendant of E, E is not the
root and F is not a leaf, we can choose E to delete;
similarly, we can choose F too. Deleting the node F
from
T
3.1
, the resulting answer-tree, T
4
, is as shown
in Fig. 10. Now, as the only child of E is a leaf, E
can’t be deleted anymore.
For each answer-tree
T
3.x
and for T
4
, let v ∈ N be
an internal node and u
1
,...,u
m
∈ N be its child nodes.
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
382


Stud(J) A
Q(J,8)
Sta f (J) B
[B] ¬Acad(J) E
Q(J,2)
Q(J,8)
Vis(J)
Q(J,4)
Figure 10: Answer-tree T
4
.
Denote by C(v) the conjunction of literals λ(a) such
that a ∈
P(v). Then,
C(v) ∧ λ(v) → λ(u
1
) ∨ ...∨ λ(u
m
)
follows from the knowledge base.
Step 6. In answer-tree
T
4
=(N, A, λ, r), let
q
1
, q
2
,...,q
n
∈ N be the nodes labeled with question-
literals. For each q
i
, i = 1,...,n, let b
i,1
,...,b
i,m
∈ N
be the brother nodes of q
i
in T
4
.Ifm ≥ 1, i.e., q
i
is
not an only child in
T
4
, then create a new node b
i,m+1
brother of b
i,1
,...,b
i,m
and make q
i
the child node of
b
i,m+1
. Assign the following label to b
i,m+1
:
• λ(b
i,m+1
)=λ(b
i,1
) ∧ ...∧ λ(b
i,m
).
This process must be repeated until all nodes labeled
with question-literals are only childs. For our ex-
ample, the answer-tree
T
5
thus obtained is shown in
Fig. 11.

Stud(J)
Q(J,8)
Sta f (J)
¬Acad(J)
Q(J,2)
Acad(J)
Q(J,8)
Vis(J)
Q(J,4)
Figure 11: Answer-tree T
5
.
In answer-tree T
5
=(N, A, λ, r),ifv ∈ N is an
internal node, a
1
,...,a
n
are its ancestor nodes and
u
1
,...,u
m
∈ N are its child nodes, then
λ(a
1
) ∧ ...∧ λ(a
n
) ∧ λ(v) → λ(u
1
) ∨ ...∨ λ(u
m
)
follows from the knowledge base.
The tree in Fig. 11 is the final answer-tree ob-
tained by the algorithm and, thus, corresponds to a
case-based answer. Each path on the tree from the
root to a leaf node corresponds to an implication
α → P(T
i
), where α is formed by making a conjunc-
tion of all literals from the root to the leaf’s father and
P(T
i
) is the question-literal labeling the leaf.
In our example, to the question “Find y such
that Q(J,y)” (“How many books can John borrow?”),
we extract the following case-based answer from the
answer-tree illustrated in Fig. 11:
∗ Stud(J) → Q(J,8)
If John is a student, then John can borrow 8 books.
∗ Staf(J) ∧¬Acad(J) → Q(J,2)
If John is a staff member and John is not an academic,
then John can borrow 2 books.
∗ Staf(J) ∧ Acad(J) → Q(J,8)
If John is is an academic staff member, then John can
borrow 8 books.
∗ Vis(J) → Q(J,4)
If John is a visitor, then John can borrow 4 books.
5 CONCLUSIONS
A disjunctive answer of the form P(T
1
) ∨ P(T
2
)∨
∨... ∨ P(T
k
), k ≥ 2, although correct, may not be in-
formative enough. The reason is that, when supplied
with such answer, the user may not be able to deter-
mine which of the elements P(T
i
),1≤ i ≤ k, of the
disjunction is an appropriate answer to his question.
Thereby, the basic motivation of this work was to pro-
vide a more informative answer to the question posed
by the user on the situations where the inference sys-
tem would normally provide us with a disjunctive an-
swer.
As defined in this work, a case-based answer to a
general question P(X) consists of an answer given in
terms of a finite number of cases, each one implying a
non disjunctive answer P(T
i
). The cases are extracted
from a proof-tree, a structure that maintains enough
information to admit such extraction.
In this current paper, we propose an algorithm
that, from a deduction of P(T
1
) ∨ P(T
2
) ∨ ... ∨ P(T
k
),
k ≥ 2, on the form a proof-tree, extracts a case-based
answer to the question, of the form
α
1
→ P(T
i
1
)
α
2
→ P(T
i
2
)
...
α
m
→ P(T
i
m
)
1 ≤ i
1
, i
2
,...,i
m
≤ k, where α
1
∨α
2
∨...∨α
m
is a log-
ical consequence of the knowledge base and α
j
is a
case that implies the answer P(T
i
j
).
It is interesting to note that there is a connection
between our case-based answer and what is called ab-
ductive explanation (Brachman and Levesque, 2004).
EXTRACTING CASE-BASED ANSWERS FROM CLOSED PROOF-TREES
383

Given a (consistent) knowledge base KB and a for-
mula β to be explained, an abductive explanation of
β is a formula α such that
KB∪{α}|= β, or equiva-
lently,
KB|=(α → β), and KB∪{α} is consistent.
Therefore, we can say that the cases α
1
, α
2
,...,α
m
are special abductive explanations to each disjunct,
since α
1
∨ α
2
∨ ... ∨ α
m
is a logical consequence of
the knowledge base.
Another condition usually required for α to be
qualified as an abductive explanation is that α is in
the appropriate vocabulary, with the purpose that α
makes sense to the user as an explanation. This con-
dition can (and should) be used in a deterministic ver-
sion of the algorithm here presented for the choice of
the cases: depending on the choice of the cases, they
may be useful or not. Thus, in practice, it is impor-
tant to add to the system some knowledge about the
vocabulary that allows appropriate choices.
As future work, we intend to generalize the
method to apply it to non closed proof-trees, possibly
using as reference the work of Burhans and Shapiro
(Burhans and Shapiro, 2007), which was developed
for inference procedures based on resolution.
REFERENCES
Brachman, R. and Levesque, H. (2004). Knowledge Repre-
sentation and Reasoning (The Morgan Kaufmann Series
in Artificial Intelligence). Morgan Kaufmann.
Bruynooghe, M. (1982). The memory management of pro-
log implementations. In Clark, K. L. and T¨arnlund, S.-
A., editors, Logic Programming, pages 83–98. Academic
Press, London.
Burhans, D. T. and Shapiro, S. C. (2007). Defining answer
classes using resolution refutation. J. Applied Logic,
5(1):70–91.
Chang, C.-L. and Lee, R. C.-T. (1997). Symbolic Logic and
Mechanical Theorem Proving. Academic Press, Inc., Or-
lando, FL, USA.
Demolombe, R. (1992). A strategy for the computation
of conditional answers. In ECAI ’92: Proceedings of
the 10th European conference on Artificial intelligence,
pages 134–138, New York, NY, USA. John Wiley &
Sons, Inc.
Green, C. C. (1969). The application of theorem proving to
question-answering systems. PhD thesis, Stanford, CA,
USA.
Letz, R. and Stenz, G. (2001). Model elimination and
connection tableau procedures. In Robinson, J. A. and
Voronkov, A., editors, Handbook of Automated Reason-
ing, pages 2015–2114. Elsevier and MIT Press.
Loveland, D. W. (1969). A simplified format for the
model elimination theorem-proving procedure. J. ACM,
16(3):349–363.
Loveland, D. W. (1978). Automated Theorem Proving: A
logical Basis. North–Holland.
Vieira, N. J. (1987). M´aquinas de Inferˆencia para Sistemas
Baseados em Conhecimento. PhD thesis, PUC/RJ. In
portuguese.
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
384