INTELLIGENT VISION FOR MOBILE AGENTS

Contour Maps in Real Time

Tariq Khan, John Morris and Khurram Jawed

Electrical and Computer Engineering, The University of Auckland, Auckland, New Zealand

Keywords:

Contour maps, Real time stereo, Dynamic scene navigation.

Abstract:

Real time interpretation of scenes is a critical capability for fast-moving intelligent vehicles. Generation of

contour maps from stereo disparity maps is one technique which allows rapid identiﬁcation of objects. Here,

we describe an algorithm for generating contour maps from disparity maps produced using an implementation

of the Symmetric Dynamic Programming Stereo algorithm in an FPGA. The algorithm has three steps: (a)

a median ﬁlter is applied to the disparity map to remove the streaks characteristic of dynamic programming

algorithms, (b) irrelevant pixels in the centre of regions are marked and (c) selected contours outlined. Results

for high resolution images (∼ 1Mpixel) show that a number of critical contours can be generated in less than

30ms permitting object outlining at video frame rates. The algorithm is easily parallelized and we show that

multiple core processors can be used to increase the number of contours that can be generated.

1 PREAMBLE

Current state-of-the-art processors do not have suf-

ﬁcient processing power to process high resolution

stereo pairs with large disparity ranges in real time.

To solve this problem, we implemented the Symmet-

ric Dynamic Programming Stereo (SPDS) algorithm

(Gimel’farb, 2002) in reconﬁgurable hardware: our

system generates disparity and occlusion maps from

one megapixel images in real-time (30fps) (Jawed

et al., 2009; Morris and Gimel’farb, 2009). This

leaves the host processor free to interpret the dispar-

ity maps and add the ability to recognize and track

objects in complex dynamic scenes in real time. As

a ﬁrst step to adding real intelligence to a mobile

agent (intelligent mobile robot, autonomous automo-

bile, etc.), we describe a contour map generation al-

gorithm which processes the disparity maps produced

by the SDPS hardware in real time. Whereas tradi-

tional segmentation approaches will generate multi-

ple segments for a textured object which then need

to be merged using other information (e.g. optical

ﬂow), generation of the contour maps (effectively a

segmentation of the disparity map) directly generates

information about the object geometry which can be

used for recognition or tracking.

1.1 Related Work

Active contour techniques which try to ﬁt contours to

image features are well known but they have several

drawbacks: they are sensitive to initialization, may

stop on incorrect local minima and do not handle tex-

tured backgrounds containing multiple objects at all

(Kass et al., 1988; Williams and Shah, 1992; Xu and

Prince, 1998). Kim et al. used a similar approach on

disparities derived from stereo pairs but they were un-

able to obtain real time performance (Kim et al., 2005;

Kim et al., 2006).

2 SYMMETRIC DYNAMIC

PROGRAMMING STEREO

We include here a brief description of the SDPS algo-

rithm, highlighting its characteristics which are rel-

evant to the current work. A key difference in its

approach is that, rather than create a disparity map

corresponding to the left or right image as the refer-

ence image, it creates the disparity map that would be

seen by a Cyclopæan ‘eye’ placed midway between

the two cameras. This enables it to place some vis-

ibility constraints on the allowed transitions between

states for each pixel. Examination of Figure 1 shows

391

Khan T., Morris J. and Jawed K. (2010).

INTELLIGENT VISION FOR MOBILE AGENTS - Contour Maps in Real Time.

In Proceedings of the 2nd International Conference on Agents and Artiﬁcial Intelligence - Artiﬁcial Intelligence, pages 391-397

DOI: 10.5220/0002738503910397

 SciTePress

p=3

B B

B ML

p=6

p=5

p=4

4 5 63210 4 5 63210

3 5 974 6 8

Figure 1: SDPS ‘view’ showing part of the Cyclopæan im-

age seen by the virtual Cyclopæan camera (centre) and a

scene object proﬁle. Visibility states (ML, B or MR) are

marked on the proﬁle. Even if there is an abrupt change in

disparity, SDPS, in common with other stereo correspon-

dence algorithms, cannot distinguish between the triangular

proﬁle shown here and the one with an abrupt change.

that, in the Cyclopæan image, a transition between

two disparity levels, p

and p

, should result in ex-

actly |p

− p

| occluded pixels marked ML (monoc-

ular left) or MR (monocular right) in the diagram in

the Cyclopæan image. This simpliﬁes for the hard-

ware implementation: the predecessor array elements

are only two bits each - encoding the ML, MR or B

(binocularly visible) state on each path - and saving

space for the most ‘expensive’ element of the whole

circuit. The dynamic programming back-track, which

generates the optimal path, relies on the state tran-

sition rules(Gimel’farb, 1991) to generate the stream

of disparities. The hardware implementation is fully

described elsewhere(Morris et al., 2009; Morris and

Gimel’farb, 2009; Jawed et al., 2009). An additional

feature of the SDPS algorithm is that it generates oc-

clusion maps at no additional cost: they are a natural

by-product of the SDPS algorithm(Morris et al., 2009;

Gimel’farb, 1991). They clearly outline objects in the

scene and, as we show here, useful to speed up scene

interpretation.

3 CONTOUR MAP GENERATION

We process the disparity maps generated by the SDPS

hardware in three steps: two pre-processing steps -

median ﬁltering (see Section 3.1) and C-state assign-

ment (see Section 3.2) - followed by the ‘Salmon’

algorithm which generates the contour maps them-

selves, described in Section 4.

3.1 Median Filtering

SDPS, like other dynamic programming stereo algo-

rithms, produces ‘streaks’ in the disparity maps be-

cause the occlusion penalty prevents a change in dis-

parity. Since these streaks often occupy a single scan

line, most of them are removed by applying a vertical

median ﬁlter to the generated disparity map.

3.2 C-state Assignment

In this phase, pixels are classiﬁed according to their

visibility states:

B binocularly visible - seen by both cameras

ML monocular left - seen by the left camera only

MR monocular right - seen by the right camera

only

C centre - of regions of equal disparity

The ﬁrst three are the same states that the SDPS

algorithm uses. The ‘C’ state is added to classify

pixels which cannot lie on contour lines and are

ignored in most steps of the Salmon algorithm.

ON-EDGE INSIDE

OUTSIDE

Figure 2: Order in which the neighbours are visited for each

of the three salmon states for a salmon ‘descending’ (π ≤

θ ≤ 2π) an ML edge. The order is reversed for a salmon

‘climbing’ (0 ≤ θ ≤ π) an MR edge.

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

392

4 SALMON

Our algorithm is modeled on the incredible journey

of a salmon downstream to the ocean, returning the

same spot as an adult

: our salmon leaves a trail of

points behind it as it traces the contour and returns to

its starting place.

For any given contour at disparity p, choose the ﬁrst

ML point from the ﬁrst scan line with a point at dis-

parity p in the linked list generated when C states

were assigned.

Denote the salmon’s current location by P

and the

disparity at P

by p

. The salmon states during con-

tour generation are designated ON − EDGE, INSIDE

or OUTSIDE. Table 1 deﬁnes these states.

The salmon’s full state is deﬁned by a 4-tuple:

(s, p

, up, r

max

)

where s ∈ {ON − EDGE, INSIDE, OUTSIDE} is

the salmon state, p

is the disparity for which the

salmon is constructing a contour, up is either true

(tracing MR contour) or false (tracing ML contour)

and r

max

is maximum extent of the salmon’s sight -

a measure of how many neighbours the salmon will

examine in this iteration. For sight, j| j = 1, ..., r

max

the salmon will examine N = 4 j + 1 neighbours. The

directions of the neighbours, φ

are deﬁned by:

= when (up = true) 0 else π

= φ

i−1

4 j

, i = 1, 2, . . . , N

where φ = 0 represents the direction along the x axis

and φ increases in an anti-clockwise direction.

The salmon’s initial state will be ON-EDGE. Our

salmon then follows the p

contour and returns to

where it started: it uses rules derived from the vis-

ibility constraints (Gimel’farb, 1991). From an MR

pixel, the salmon moves up - 0 ≤ φ ≤ π. From an ML

pixel, the salmon moves down so that π ≤ φ ≤ 2π. The

salmon uses steps j = 1, .., r

max

to decide in which di-

rection it should move. If it can not decide at step j

then it tries step j + 1.

4.1 General Rules

1. Any point in C state is ignored.

2. A neighbour at j always has higher priority than

neighbours at j + 1.

”Salmon make an incredible journey downstream

from the fresh water where they are born, to the

ocean, and then back upstream again as adults,

ﬁnding the exact location where they began sev-

eral years earlier.” (U.S. Bureau of Land Manage-

ment http://www.blm.gov/education/00_resources/

articles/Columbia_river_basin/posterback.html)

3. Transition to an ON-EDGE state always has high-

est priority.

4. Transition to an INSIDE state always takes prior-

ity over transition to an OUTSIDE state.

5. If there are two or more possible transitions to IN-

SIDE neighbours than the neighbour with closest

disparity will be chosen.

6. If there are two or more possible transitions to

OUTSIDE neighbours than the neighbour with

closest disparity will be chosen.

7. If the current state is ON-EDGE or INSIDE then

ML or MR is chosen over B with same disparity.

8. If the current state is OUTSIDE then B is chosen

over ML or MR with the same disparity.

4.2 Search Priority

For each salmon state, the order in which the neigh-

bours are searched is different: the priorities for the

salmon moving down and for j = 1 are shown in Fig-

ure 2.

4.3 Expanding the Search Region

If all the neighbours of a point are marked C or have

been visited, then we increment j and search in a

wider region. To prevent the salmon from selecting

the wrong neighbour, a maximum iteration count is

speciﬁed. If this count reaches a predeﬁned limit or

the salmon returns to its starting point, the contour

will be terminated and added to the contour list.

4.4 Salmon Operation

An example salmon run is shown in Figure 3. The

salmon starts in the (7,ML) pixel at the top and works

down, trying to stay on the (7,ML) ‘edge’.

However, it is not possible always: in row 2, the

salmon is ON-EDGE, but there is no (7,ML) neigh-

bour, so the salmon will use the priority scheme

shown in Figure 2 and go INSIDE to (8,B) attempting

to ﬁnd another (7, ML) point.

In row 4 at (7, ML), again there is no adjacent (7, ML)

so the salmon will go OUTSIDE to (6, B) and follow

the priorities shown in Figure 2 to ﬁnd (7,ML) again.

Then a sequence of (7,ML) pixels are followed until

at row 9, the salmon is facing a continuous wall of C

pixels. It is forced to go INSIDE and swim through

a sequence of (7,B) pixels (a horizontal edge), even-

tually ﬁnding a (7, MR) one. At this point, it reverses

the direction and ‘climbs’ the (7, MR) edge back to

the starting point.

INTELLIGENT VISION FOR MOBILE AGENTS - Contour Maps in Real Time

393

Table 1: Salmon state deﬁnitions.

State Deﬁnition Action

ON-EDGE on an edge: P

is in ML or MR state

with p

= p

continue along the edge

INSIDE inside a contour: P

is in B state

with disparity equal to p

or p

> p

when going (down | up), go outwards (to the

(le f t | right)) to ﬁnd the p

edge

OUTSIDE outside: p

< p

when going (down | up), go inwards (to the

(right | le f t)) to ﬁnd the p

edge

Figure 3: Example Salmon ‘run’: boxes represent pixels

in the disparity and occlusion maps - they are labeled with

the disparity and the visibility state after C states have been

assigned. The background pattern for each pixel shows

the salmon state as it visits a pixel - see the legend. The

salmon starts with the highlighted (7,ML) pixel at the top,

‘descends’ through ML pixels and climbs back (not shown)

through MR pixels to reach its starting point again.

4.5 Horizontal Edges

Objects with horizontal edges present the largest chal-

lenge to the Salmon algorithm: they show large dis-

parity jumps between scanlines and can have large

regions of B pixels adjacent to B pixels with a dif-

ferent disparity, i.e. there are no ML or MR pixels

delineating the contour. A disparity map for a syn-

thetic scene with horizontal edges is shown in Figure

4. Figure 5(a)-(h) shows in detail the behaviour at

each transition to a horizontal edge. Note that when

there are large disparity changes in the vertical direc-

tion, several contours will, as expected, run through

the same pixels. In Figure 5(a), the p = 6 contour en-

ters the INSIDE state and then turns left, preferring

the (6,B) pixels over the (6,C) pixels (which must con-

stitute the centre of a plane). This contour will even-

tually encounter (6,ML) pixels (Figure 5(e)) enter the

ON-EDGE state and continue normally. The p = 7

contour prefers the (8,ML) pixel to its right (rule 4

because the (6,B) pixel would be an OUTSIDE state

for it) and follows the (8,B) pixels in an INSIDE state

until it encounters a (7,MR) pixel (Figure 5(b)) and

changes direction. The p = 8 contour also prefers the

(8,B) pixel because the (7,ML) pixel is OUTSIDE for

it.

In Figure 5(b), the p = 8 and p = 7 contours ﬁnd

their correct MR ‘edges’, separate and climb the MR

edge. The p = 6 contour reaches a (6,MR) pixel and

climbs. In Figure 5(c), three contours ﬁnd walls of

C pixels and choose to follow the (8,B) pixels (rule

1). In Figure 5(d), three contours locate their starting

points (outlined in black) and terminate. Figure 5(d) -

(h) show a single contour avoiding a wall of C pixels.

5 RESULTS

In Table 2, we show times for pre-processing a 1024 ×

768 pixel image, whose disparity map produced by

the SDPS hardware has 2048 × 768 pixels (a conse-

quence of the Cyclopæan view). These stages are

readily parallelized and the times for a quad core pro-

cessor are well within our target of 30 ms for real

time performance at 30fps. The contour generation

code was compiled using Visual C++’s optimizers but

little attempt was made to optimize the C code it-

self. Median ﬁltering and C state assignment could

also be sped up by using the MMX hardware within

each processor, so further improvements are certainly

possible. Since generating a set of 24 contours for

an ∼ 1Mpixel image is taking less than 10 ms, there

is signiﬁcant scope for object recognition or tracking

capabilities to be added whilst maintaining real time

performance.

Selected frames from two image sequences are shown

in Figure 6 and Figure 7. In the ﬁrst set, two con-

tours are shown - the ball and the thrower. Note

that the contour has correctly identiﬁed the thrower

as leaning forward slightly - not chopped his legs off!

In the second set, we demonstrate the capability of

our hardware-software combination to capture a small

fast moving silicone rubber ball in ﬂight!

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

394

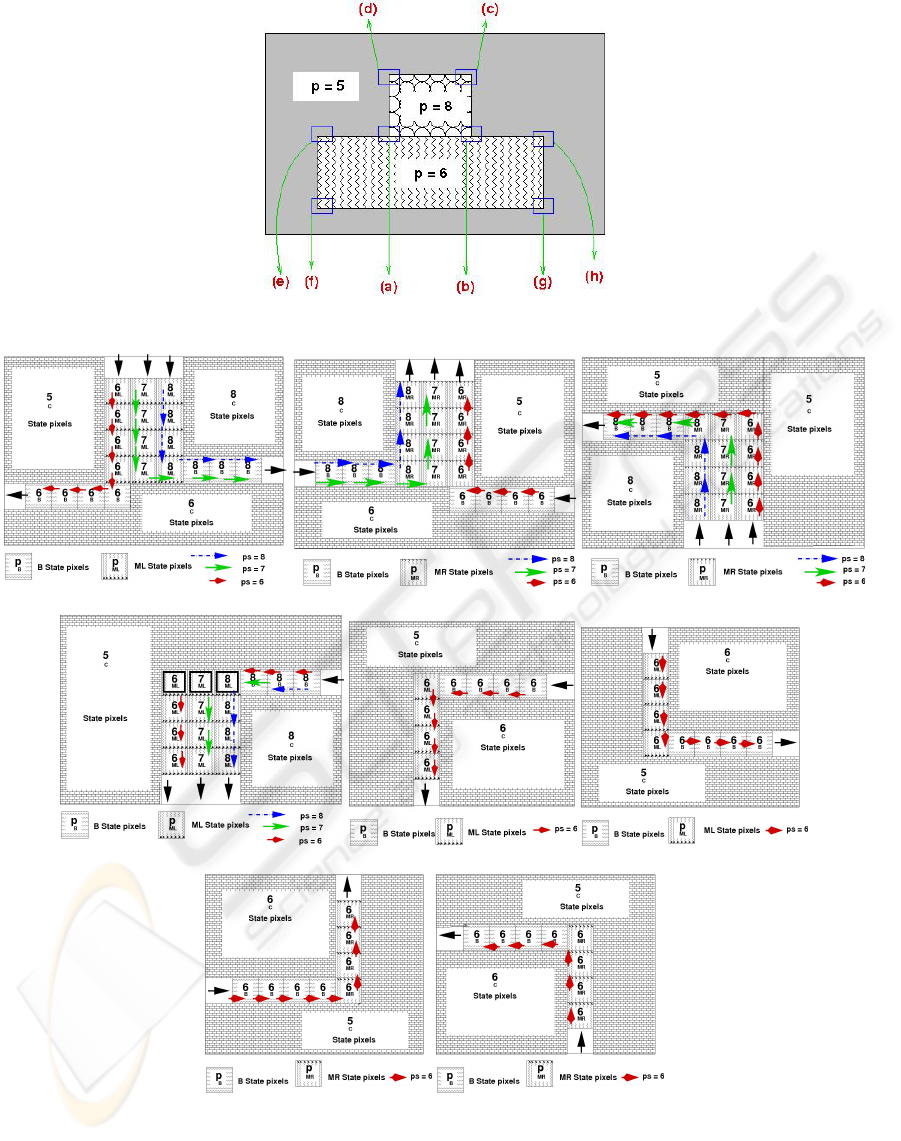
Figure 4: Disparity map for scene object with horizontal edges: the marked regions are shown in detail in Figure 5.

(a) (b) (c)

(d) (e) (f)

(g) (h)

Figure 5: Salmon operation for the regions marked in Figure 4.

6 CONCLUSIONS

Using high resolution disparity maps (original im-

ages: 1024 × 768 pixels with disparity range of 80)

produced in real time (30 fps) by an FPGA based

attached processor, the salmon is able to generate a

INTELLIGENT VISION FOR MOBILE AGENTS - Contour Maps in Real Time

395

Disparity map Occlusion map Contour map (L image)

Figure 6: Example contours - Basket ball sequence: frame rate - 30fps: two sample contours are shown for each frame. Note

that the maps are twice as wide as the original image: the SDPS algorithm produces a Cyclopæan view with twice as many

points as the original images.

Original scene

Figure 7: Example contours - silicone ball sequence. A small silicone ‘bouncy’ ball is captured in ﬂight in the lower slices

taken from the full scene (top image). The thrower and the ball are outlined. Colour images of both these and other sequences

can be viewed at http://www.cs.auckland.ac.nz/

jmor159/HRPG/RT/index.html.

number of critical contour maps in real time. The time

to generate each contour is proportional to its length

but the algorithm generates each contour indepen-

dently and is able to use the multiple cores commonly

available now to advantage. Most of the processing

time is used in median ﬁltering and C state assign-

ment: these tasks are regular and good candidates for

implementation on the FPGA - freeing further CPU

cycles for generating additional contours, matching

contours to object proﬁles or tracking objects outlined

by contours. The current SDPS implementation is

very efﬁcient and uses only a fraction of the resources

available in modern FPGAs(Jawed et al., 2009) so

that additional processing on the FPGA surface is pos-

sible. Additional FPGA processing will add a small

latency to the time between image capture at the cam-

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

396

Table 2: Execution time.

Median ﬁltering

Window Number of Cores

size 1 2 3 4

1 × 3 25 15 11 9

1 × 5 31 17 13 9

1 × 7 35 20 14 11

1 × 9 39 22 15 12

1 × 11 42 23 16 13

1 × 13 45 25 17 14

1 × 15 48 27 18 16

1 × 17 51 28 20 15

1 × 19 52 30 20 16

C state assignment 6 5 4 3.7

Contour Generation

Disparity Number

set of points

13-36 37208 8.4 7.2 6.3 -

All times in milliseconds for a 2.4GHz quad core

processor.

era and receipt of scan lines in the host processor: at

most the number of scan lines in the median ﬁlter win-

dow - typically less than 1 ms of real time.

REFERENCES

Gimel’farb, G. (1991). Intensity-based computer binocu-

lar stereo vision: signal models and algorithms. Int J

Imaging Systems and Technology, 3:189–200.

Gimel’farb, G. (2002). Probabilistic regularisation and

symmetry in binocular dynamic programming stereo.

Pattern Recognition Letters, 23(4):431–442.

Jawed, K., Morris, J., Khan, T., and Gimel’farb, G. (2009).

Real time rectiﬁcation for stereo correspondence. In

Xue, J. and Ma, J., editors, 7th IEEE/IFIP Intl Conf

on Embedded and Ubiquitous Computing (EUC-09),

pages 277–284. IEEE CS Press.

Kass, M., Witkin, A., and Terzopoulos, D. (1988). Snakes:

Active contour models. International Journal of Com-

puter Vision, 1(4):321–331.

Kim, S. H., Alattar, A., and Jang, J. W. (2006). Object con-

tour tracking using the optimization of the number of

snake points. In Int Conf on Computational Intelli-

gence and Security, volume 2.

Kim, S. H., Jang, J. W., Lee, S. P., and Choi, J. H.

(2005). Accurate contouring technique for object

boundary extraction in stereoscopic imageries. LNCS,

3802:869.

Morris, J. and Gimel’farb, G. (May 6, 2009). Real-time

stereo image matching system. NZ Patent Application

567986.

Morris, J., Jawed, K., and Gimel’farb, G. (2009). Intel-

ligent vision: A ﬁrst step - real time stereovision.

In Advanced Concepts for Intelligent Vision Systems

(ACIVS’2009), volume 5807 of LNCS, pages 355–

366. Springer.

Williams, D. J. and Shah, M. (1992). A fast algorithm for

active contours and curvature estimation. CVGIP: Im-

age understanding, 55(1):14–26.

Xu, C. and Prince, J. L. (1998). Snakes, shapes, and gradi-

ent vector ﬂow. Image Processing, IEEE Transactions

on, 7(3):359–369.

INTELLIGENT VISION FOR MOBILE AGENTS - Contour Maps in Real Time

397