COMPUTER SIMULATION OF MICROELECTRODE BASED
BIO-IMPEDANCE MEASUREMENTS WITH COMSOL
Alberto Olmo
1
and Alberto Yúfera
2
1
Escuela Superior de Ingenieros (ESI), Dto. Física Aplicada III, Universidad de Sevilla
Av. de los Descubrimientos s/n. 41092. Sevilla. Spain
2
Instituto de Microelectrónica de Sevilla (IMSE), Centro Nacional de Microelectrónica (CNM-CSIC)
Universidad de Sevilla, Av. Américo Vespucio s/n. 41092. Sevilla. Spain
Keywords: Microelectrode, Bioimpedance, Impedance sensor, Computer simulation, COMSOL.
Abstract: Electrical models for microelectrode-cell interfaces are essential to match electrical simulations to real bio-
systems performance and correctly to decode the results obtained experimentally. The accurate response
simulation of a microelectrode sensor to changes in the cell-electrode system, such as cell growth, enables
the optimum microelectrode design process. We report the use of COMSOL quasi-static mode, contrary to
other DC modes frequently used, including magnetic fields to calculate the bioimpedance of the system. A
fully electrode-cell model has been built, and the effect of fibroblasts of different diameters on the simulated
impedance of small microelectrodes (32-µm square) has been studied, in order to validate the model and to
characterize the microelectrode sensor response to changes in cell size and density.
1 INTRODUCTION
Many biological parameters and processes can be
sensed and monitored using its impedance as marker
(Beach et al., 2005), (Yúfera et al., 2005), (Yúfera et
al., 2008), (Radke and Alocilja, 2005), with the
advantage of being a non-invasive and relatively
cheap technique. Cell growth, changes in cell
composition or changes in cell location are only
some examples of processes which can be detected
by microelectrode-cell impedance sensor variations.
Electrical models have been reported for the
electrode-cell interfaces (Huang et al., 2004),
(Borkholder, 1998), (Joye et al, 2008), being these
key for matching electrical simulations to real
systems performance and hence decoding correctly
the results obtained experimentally, usually known
as reconstruction problem.
Some of these models have been obtained by
using the finite element analysis method with
programs such as FEMLAB. (Huang et al., 2004).
The use of the DC mode for a sinusoidal steady state
calculation is possible by assigning a complex
conductivity, which works because the Poisson
equation is the same form as the Laplace equation in
the charge-free domain. This paper presents an
alternative method for simulating electrode – cell
interfaces with finite element analysis, based on
COMSOL. The quasistatic mode of COMSOL is
used, which also takes into account magnetic fields
to calculate the electric impedance.
Our work, based on previous models (Huang et
al., 2004), is developed in section 2. Several
improvements on their model have been made both
on the cellular membrane and the cell-electrode gap,
are described in section 3. Impedance changes on
small electrodes (32- µm square) caused by different
sizes of 3T3 mouse fibroblasts were simulated in
section 4, in order to validate the model and
characterize the microelectrode sensor response to
cell growth. Finally, conclusions are highlighted in
section 5.
2 CELL-ELECTRODE MODEL
The work performed by Huang et al. (Huang et al.,
2004), was initially explored, making use of the
computation advantages COMSOL provides over
FEMLAB. Our objective is to compare the results in
the study of the impedance changes caused by cell
growth on electrodes with similar size to the cell.
Cells modelled in the simulation by Huang et al.
were 3T3 mouse fibroblasts, which attach closely to
178
Olmo A. and Yúfera A. (2010).
COMPUTER SIMULATION OF MICROELECTRODE BASED BIO-IMPEDANCE MEASUREMENTS WITH COMSOL.
In Proceedings of the Third International Conference on Biomedical Electronics and Devices, pages 178-182
DOI: 10.5220/0002740301780182
Copyright
c
 SciTePress

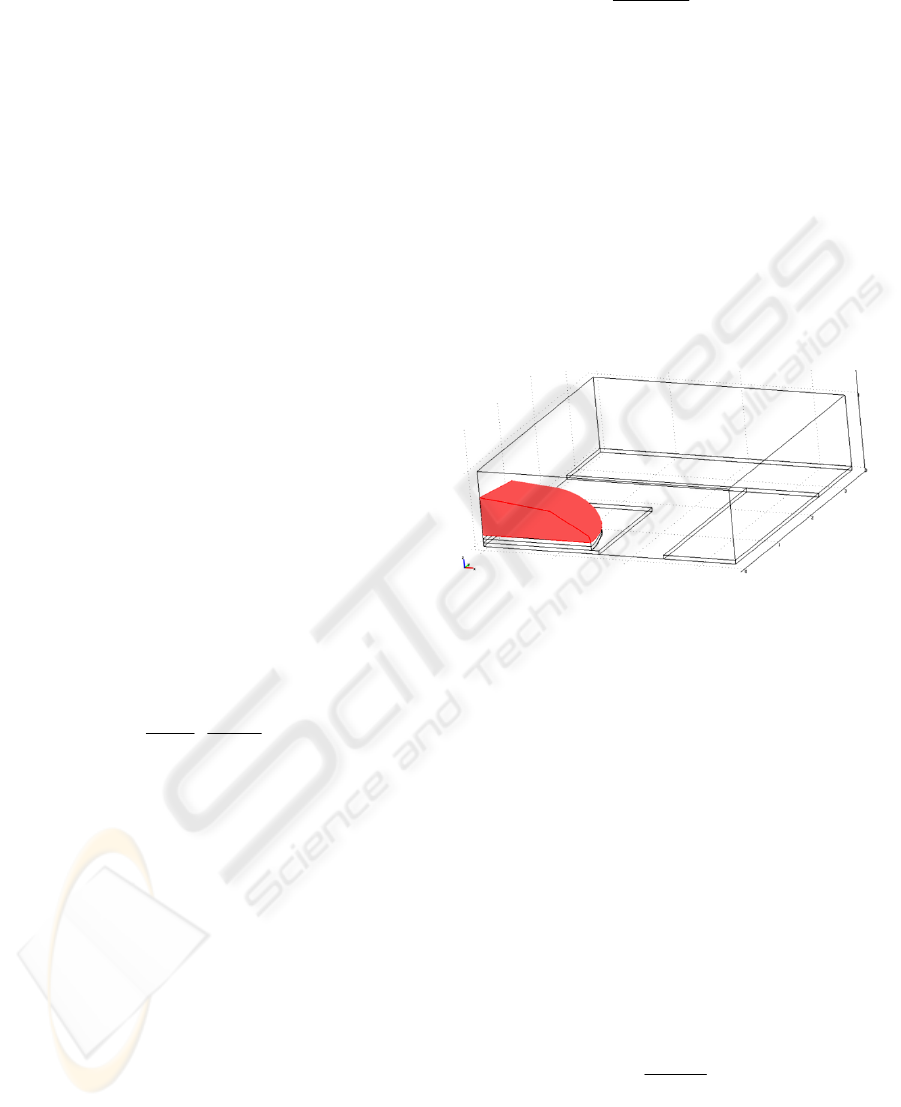
surfaces and which have a cell-surface separation
typically of 0.15µm (Giebel et al., 1999). The cells
are about 5µm in height and, from a top view, are
irregularly shaped and approximately 30–50µm in
extent. A circular cell 30 µm in diameter centred on
a square sensing electrode that is 32µm on each side
was considered. (see figure 1). The sensing electrode
was surrounded by a counter electrode that has
considerably greater area.
3T3 mouse fibroblasts consist of a thin (about 8
nm), poorly conducting membrane that surrounds
the highly conductive interior of the cell. The
capacitance of the cell membrane is approximately
C
mem
= 1 µF/cm
2
(Geddes, 1972). The cell culture
medium simulated by Huang et al. is highly ionic
and possesses a conductivity of approximately 1.5
S/m. The cell culture medium fills the cell-electrode
gap and forms an electrical double layer (Helmholtz
plus diffuse layer) between the bulk of the medium
and the electrode that is approximately 2 nm in
thickness.
Some approximations were made in X. Huang´s
work to facilitate the resolution of the problem by
FEMLAB. Only one quarter of the electrode was
simulated. As the problem is characterized by a wide
range of distance scales, it was difficult to solve by
finite-elements techniques, so the following
adjustments were made:
 The electrical double layer modelling the
electrode-solution equivalent circuit was
replaced with a 0.5 µm thick region with the
same specific contact impedance
1/2 1/2
(2 ) (2 )
22
dl dl I
ww
fjf
jf t jC f
KK
ππ
σπε π
⎡⎤
+=⋅ + +
⎢⎥
⎣⎦
(1)
Where σ
dl
and ε
dl
are the conductivity and
dielectric permittivity of the double layer, t is the
thickness of the region, C
I
is the interfacial
capacitance per unit area, which consists of the
series combination of the Helmholtz double layer
and the diffuse layer, and K
w
is a constant related
with Warburg impedance contribution.
 The cell membrane was replaced by a 0.5 µm
thick region with the same capacitance per
unit area
memmem
Ct
⋅
=
ε
(2)
Where C
mem
is the membrane capacitance per unit
area and t = 0.5µm.
 Electrode-cell gap was replaced with a 0.5 µm
thick region with the same sheet conductivity,
that is
medium
electrodecell
gap
t
t
σσ ⋅=
−
(3)
Where t
cell-electrode
is the gap thickness and t is
again 0.5µm.
In our work, the geometry of their simulation
was adopted (see figure 1), and the values for the
conductivity and permittivity of the electrical double
layer were calculated following the same expression
shown before (1), with the same values for K
w
and
C
I
mentioned in the article (Huang et al., 2004).
Conductivity of the cell and the medium was
also set to 1.5 S/m in our work. However, the model
by X. Huang et al. for the electrode-cell gap and the
cellular membrane (equations 2 and 3) was refined
as shown in the following section.
Figure 1: Geometry of the model simulated in COMSOL.
3 MODEL ENHANCEMENT
Several modifications were made in the model in
order to obtain simulations of cell impedance
measurements with more accuracy and obtaining a
more complex model that reflects real experiments
in a more realistic way. Such modifications were
made in the following areas:
3.1 Cellular Membrane
The equivalent circuit of the attached membrane was
modelled as a resistance R
m
in parallel with a
capacitance C
m
, in a similar way as reported by Joye
et al. (Joye et al. 2008). These parameters are
defined as
AcC
Ag
R
memm
mem
m
⋅=
⋅
=
1
(4)
Where A is the area of the attached membrane
(in our case A=706.86e-12 m
2
), g
mem
= 0.3 mS/cm
2
is the local membrane conductivity and c
mem
(1
COMPUTER SIMULATION OF MICROELECTRODE BASED BIO-IMPEDANCE MEASUREMENTS WITH
COMSOL
179

µF/cm
2
) is the membrane capacity per unit area
(Joye et al. 2008).
Making use of the following expression we can
calculate the conductivity and permittivity of the
cellular membrane from the impedance.
)(
1
ωεσ jK
Z
+
=
(5)
Where K is the geometrical factor (K = area /
length). In our case a value of 5 µm has been taken
as the length. (This value corresponds to the
thickness of the membrane layer represented in
COMSOL). The value for K results 1413e-6, and the
values obtained for conductivity and permittivity are
σ =1.5e-6 S/m and ε = 5.001e-9 F/m (ε
r
=565).
3.2 Cell Membrane-electrolyte
Interface Capacitance
This capacitance was not considered in Huang´s
model, but can also be important, as it models the
charge region (also called the electrical double layer)
which is created in the electrolyte at the interface
with the cell. The capacitance C
hd
is defined as the
series of three capacitances:
0
1
0
2
20
0
2
IHP
hce
IHP
OHP
hce
OHP IHP
d
dce
CA
d
CA
dd
qKTznN
CA
KT
εε
εε
εε
=
=
−
=
(6)
Where A
ce
is the area of the attached membrane,
ε
0
is the dielectric permittivity of free space; ε
IHP
and
ε
OHP
are respectively the Inner and Outer Helmholtz
Plane relative dielectric constant; d
IHP
is the distance
of the Inner Helmholtz Plane to the membrane; d
OHP
is the distance of the Outer Helmholtz Plane to the
membrane; ε
d
is the diffuse layer relative dielectric
constant; K
B
is Boltzmann’s constant; T is the
absolute temperature; q is the electron charge; z is
the valence of ions in solution; n
0
is the bulk
concentration of ions in solution; and N is
Avogadro’s number.
For C
hd
, the values given in Joye´s report (Joye
et al. 2008) are considered. In particular, it is
assumed that ε
IHP
= 6, ε
OHP
=32, d
IHP
= 0.3 nm, d
OHP
= 0.7 nm, z = 1, T = 300 K, and n
0
=150 mM. The
area of the attached membrane is in our case
A
ce
=706.86e-12 m
2
. and ε
d
is set to 1. The following
values were obtained:
C
h1
= 0.125pF; C
h2
=0.5pF; C
d
=2.22pF
And the total series capacitance was C
hd
=1.54pF.
Comparing the impedance equivalent to this
capacitance with the same expression as before (5),
and modelling again this layer as a 5 µm thick layer
with K =1413e-6, we obtained ε = 0.0011e-6 F/m,
which corresponds to ε
r
= 124.29, value that was
inserted in COMSOL.
4 SIMULATION RESULTS WITH
COMSOL
As can be seen in figure 1, only one quarter of the
electrodes and cell was simulated. Electrodes were
modelled with no thickness. The first layer modelled
on top of the electrode surface is the electrical
double layer, of 0.5 µm thickness, which can be seen
in the figure. On top of the electrical double layer,
the cell-electrode gap is modelled with another 0.5
µm layer. This layer includes in our simulation the
cell membrane-electrolyte interface capacitance. On
top of it we finally have the cell membrane, also
modelled as another 0.5 µm layer, and the rest of the
cell. For each layer, it is necessary to introduce in
COMSOL the conductivity and permittivity values
calculated before.
All surfaces had an insulating boundary
condition (n*J=0) with the exception of the surfaces
separating the different layers and sub-domains
within the model, which were set to continuity
(n*(J
1
-J
2
) = 0) and the bottom surface of the two
electrodes, which were set to an electric potential of
1V and 0V.
The Quasi-statics module of COMSOL was used
to perform the finite element simulations. In this
mode, it is possible to obtain the solution for the
electric potential for different frequencies.
Simulations were performed on a 2.26 GHz Intel(R)
Core(TM)2 DUO CPU. Solution times varied with
the frequency but ranged from 3 to 6 minutes. In
Figure 2 we can see the solution for the electric
potential at the determined frequency of 100 Hz.
Figure 2: Electric potential solution at 100Hz.
BIODEVICES 2010 - International Conference on Biomedical Electronics and Devices
180

Two series of simulations, with frequency
ranging from 10
2
Hz to 10
6
Hz, were made with and
without the presence of the cell.
Once the solution for the electric potential had
been found by COMSOL, Boundary Integration was
used to find the electric current through the counter
electrode. With that value the electric impedance
was calculated, taking into account that the voltage
difference between electrodes was 1V and that
impedance had to by divided by 4 (as only one
quarter of the electrodes was simulated.) The values
obtained are shown in figure 3.
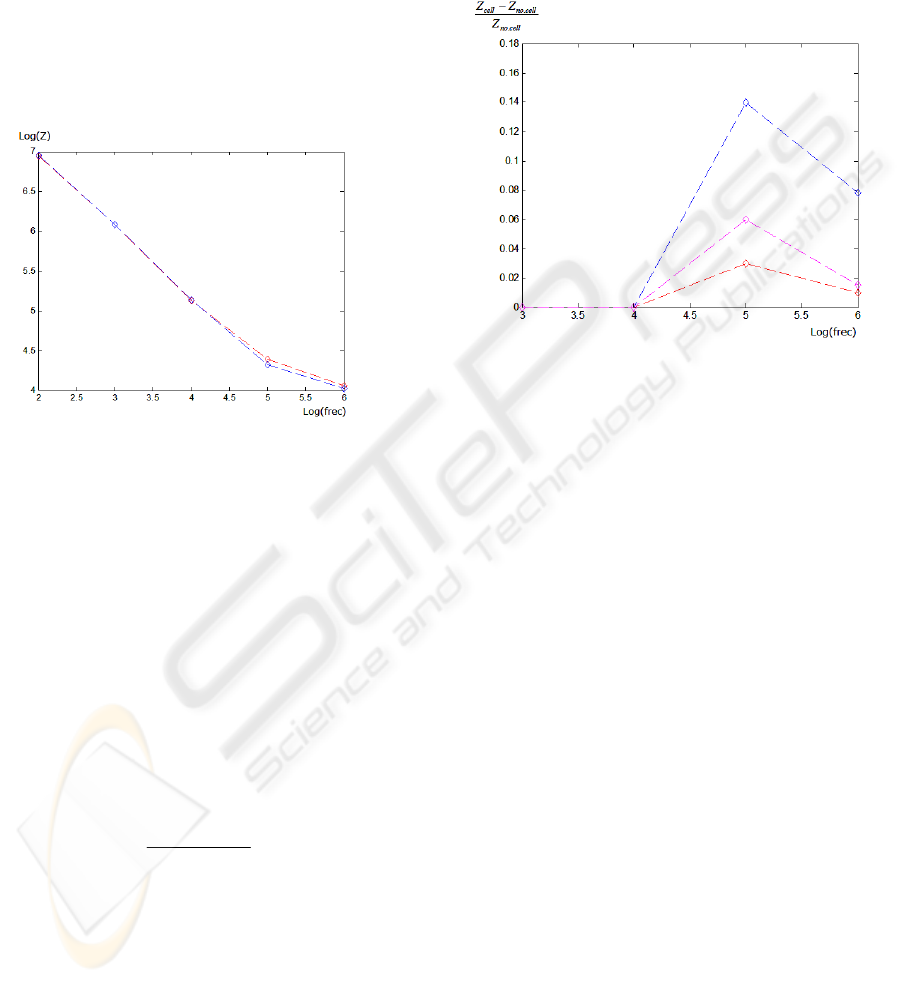
Figure 3: Impedance magnitude of the microelectrode
system with cell (red line) and without it (blue line).
The measured impedance changes by several
orders of magnitude over the frequency range
simulated, which is in accordance with previous
works (Huang et al., 2004), (Borkholder, 1998).
We can see how the presence of the cell changes the
measured impedance, with the biggest change at a
frequency near to 10
5
Hz. This is also in accordance
with the report of Huang et al.
Another way of representing the impedance
magnitude is to observe the impedance changes of
the system with cell on top respect to the
microelectrode system without cell. This can be
done by plotting the normalized impedance change,
defined as
cellno
cellnocell
Z
ZZ
r
.
.
−
=
(7)
Being Z
cell
and Z
no.cell
the impedance magnitudes
with and without cell, respectively. The normalized
impedance changes of the system with the 30µm-
diameter cell modelled before is plotted in figure 4
(blue line).
In order to have a measure of the system
sensibility to changes in cell dimension, we repeated
the calculations reported in sections 3.1 and 3.2 for
other sizes of cell. Parameters of the cell membrane
and cell membrane-electrolyte interface were
recalculated for cells of 15 µm and 20 µm of
diameter, inserted in COMSOL, and new
simulations were performed. Results are also shown
in figure 4.
Figure 4: Simulated normalized impedances of the system,
for a 30µm-diameter cell (blue line), 20µm-diameter cell
(magenta line) and 15µm-diameter cell (red line).
We observe how the system is sensitive to these
differences in cell size. At the same frequency, the
normalized impedance r increases with the cell
dimension, being an excellent indicative of the area
overlap between the microelectrode-cell and,
allowing the measurement of the cell size and/or cell
density. Normalized impedance peaks indicate the
optimum frequency for measurements. It is of 0.03
for cells of 15 µm of diameter, and 0.14 for 30 µm
of diameter at approximately 10
5
Hz. For cell
density measurements, a fill factor parameter can be
defined as a percentage of the microelectrode area
covered by cells.
These curves characterize the sensibility of the
sensor and can be useful in the preliminary design of
microelectrodes.
5 CONCLUSIONS
Electrical models for electrode-cell interfaces are the
key for matching electrical simulations to real
systems performance and correctly decoding the
results obtained experimentally, usually known as
reconstruction problem. They are also very useful to
determine the sensibility of microelectrode sensors
to different changes in processes such as cell growth.
COMPUTER SIMULATION OF MICROELECTRODE BASED BIO-IMPEDANCE MEASUREMENTS WITH
COMSOL
181

In our work, an enhance electrode-cell model
was built, based on a previous work, incorporating
the cellular membrane and the cell-electrode gap in
order to obtain more accurately simulate impedance
measurements.
The quasi-static mode of COMSOL was used to
perform the finite-element simulations. The
influence of the cell size on the measured impedance
of small electrodes (32-µm square) was studied,
obtaining the greatest impedance changes due to the
cell influence at frequencies near 10
5
Hz. The
microelectrode sensor response to cell changes in
growth was characterized.
The model and finite element method simulation
has proved to be a valid one, in agreement with other
experimental results, which can be used in the future
to simulate a wide number of biological experiments
based on bio-impedance measurements and to
characterize a large number of micro-sensors
structures.
ACKNOWLEDGEMENTS
We would like to thank Mrs. Josefa Guerrero, from the
Physics Department of the University of Seville, for her
valuable help with COMSOL simulations.
This work is in part supported by the Spanish
founded Project: TEC2007-68072, Técnicas para
mejorar la calidad del test y las prestaciones del diseño
en tecnologías CMOS submicrométricas.
REFERENCES
Beach, R.D. et al, 2005. Towards a Miniature In Vivo
Telemetry Monitoring System Dynamically
Configurable as a Potentiostat or Galvanostat for Two-
and Three- Electrode Biosensors, IEEE Trans. On
Instrumentation and Measurement, vol. 54, nº1, pp:
61-72, 2005.
Yúfera, A. et al., 2005. A Tissue Impedance Measurement
Chip for Myocardial Ischemia Detection. IEEE
Transaction on Circuits and Systems: Part I. vol.52,
nº:12 pp: 2620-2628.
Radke, S.M and Alocilja, E.C., 2004. Design and
Fabrication of a Microimpedance Biosensor for
Bacterial Detection, IEEE Sensor Journal, vol. 4, nº 4,
pp: 434-440.
Borkholder, D. A., 1998. Cell-Based Biosensors Using
Microelectrodes. PhD Thesis, Stanford University.
Huang X. et al., 2004. Simulation of Microelectrode
Impedance Changes Due to Cell Growth, IEEE
Sensors Journal, vol.4, nº5, pp: 576-583.
Yúfera A. et al., 2008. A Method for Bioimpedance
Measure with Four- and Two-Electrode Sensor
Systems, 30th Annual International IEEE EMBS
Conference, pp: 2318-2321.
Joye N. et al., 2008. An Electrical Model of the Cell-
Electrode Interface for High-density Microelectrode
Arrays, 30th Annual International IEEE EMBS
Conference, pp: 559-562. 2008
Giebel, K.F. et al., 1999. Imaging of cell/substrate contacts
of living cells with surface plasmon resonance
microscopy, Biophysics Journal, vol. 76, pp: 509–516.
Geddes, L.A., 1972. Electrodes and the Measurement of
the Bioelectrical Events, New York. Wiley.
BIODEVICES 2010 - International Conference on Biomedical Electronics and Devices
182