CONVEX SHAPE RETRIEVAL FROM EDGE MAPS BY THE USE OF

AN EVOLUTIONARY ALGORITHM

A. Nezhinsky, J. Kruisselbrink and F. Verbeek

Leiden University, LIACS, Niels Bohrweg 1, The Netherlands

Keywords:

Evolutionary algorithm, Model based segmentation, Shape retrieval.

Abstract:

There is a need for a high-throughput approach for extracting biological shapes from images. The approach

for automated extraction of convex biological shapes presented in this paper is an Evolutionary Algorithm. As

opposed to existing model based segmentation methods this approach is uniform for different images, needs

no training set and is initialized automatically. The process of ﬁnding the shape is considered an optimization

problem and for that reason an Evolutionary Algorithm was a good candidate for a solution. The results show

that the proposed Evolutionary Algorithm gives a fast solution for pattern recognition and shape extraction.

1 INTRODUCTION

Pattern recognition is crucial for the analysis of large

image datasets in bio–imaging and many success-

ful applications have been described in the litera-

ture. The ﬁrst step in many applications is to seg-

ment a meaningful biological structure from images

and remove the background, despite its position, ro-

tation and scale. Images in biology are acquired un-

der different conditions which affects quality, bright-

ness, contrast, lighting conditions and the amount of

noise. Consequently, extraction as well as processing

of shapes from the images might be hampered. For

our analysis we want to ﬁnd an uniform way to over-

come these problems.

Since many biological shapes (cell, embryo etc.) can

be approximated by a convex shape we will propose

a method for extraction of convex-shaped structures

from images. Our approach is not meant for recog-

nition and discrimination between certain predeﬁned

shapes, but for the recognition and the extraction of

the most prominent convex shape within the image.

The Evolutionary Algorithm (EA) will extract the ob-

ject with its shape closest to a convex shape and with

the best edge gradient. In most cases this is the bio-

logical structure.

Though many model based segmentation techniques

(T.F.Cootes et al., 2009), (M.Kass et al., 1987),

(F.Leymarie and M.D.Levine, 1993), (Y.N.Wu et al.,

2007), (J.A.Sethian and A.James, 1999) are already

successfully used, we want to investigate the possi-

bilities of an EA being able to extract convex shapes

from images. Thereby we want to look at the advan-

tages of an EA over other approaches and evaluate the

difﬁculties.

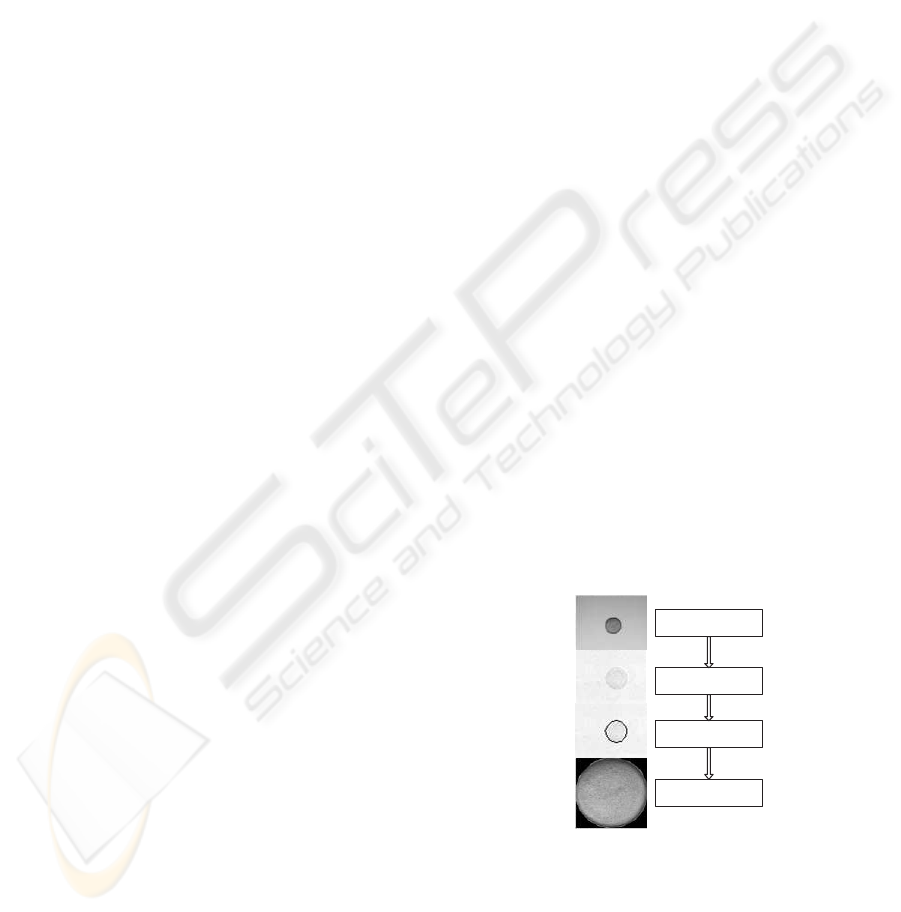
Figure 1 shows the general image process ﬂow in

which the proposed method and the preprocessing

step are incorporated for shape extraction. Edge maps

are used as input images, since edges can be used as

distinctive features for shapes. An EA is used to ex-

tract the convex shapes from these edge maps.

Input image

Edge Map

Shape fitting by EA

Resulting Image

Figure 1: Data ﬂowchart.

The paper is organized as follows. In section 2 exist-

ing approaches are discussed. Section 3 gives a short

overview of our approach. Section 4 addresses the

proposed EA used for shape recognition. In sections 5

experimental results are shown and they are discussed

in section 6.

221

Nezhinsky A., Kruisselbrink J. and Verbeek F. (2010).

CONVEX SHAPE RETRIEVAL FROM EDGE MAPS BY THE USE OF AN EVOLUTIONARY ALGORITHM.

In Proceedings of the First International Conference on Bioinformatics, pages 221-225

DOI: 10.5220/0002742502210225

 SciTePress

2 EXISTING APPROACHES

Most widely used methods are: active shape mod-

els (ASM) (T.F.Cootes et al., 2009); (F.J.Verbeek

et al., 2004), active snakes (or contours) (M.Kass

et al., 1987) (F.Leymarie and M.D.Levine, 1993), de-

formable templates (Y.N.Wu et al., 2007) and level-

set based methods (LSM) (J.A.Sethian and A.James,

1999).

Most model based segmentation methods are con-

cerned with the retrieval of certain pre–deﬁned shapes

from the images.

A classic ASM approach needs a large training set.

Instances not matching the training set may fail. In

our approach no training set is needed.

With the ASM, deformable templates and the active

snake approach the initialization of the shape model

must be located close to the shape we are looking for.

The LSM approach and some other approaches also

suffer from high computational complexity.

3 APPROACH OVERVIEW

We want to develop an approach which is very ﬂexi-

ble. While existing approaches like active snakes are

very ﬂexible models, we want an even more ﬂexible

one, where the initialization shape does not need to

be set (besides that it is a convex shape) and no train-

ing set is needed. An approach that does not require

predeﬁned shapes for initialization could be applied

to different kind of images without any signiﬁcant pa-

rameter change.

3.1 Image Preprocessing

Edge location within each image is efﬁciently repre-

sented by the magnitude of the gradient, which will be

the basis for the shape retrieval. Therefore we trans-

form the input image into a gray scale or a binary

representation from which the edge map is computed.

Any state of the art edge detector can be used for this

purpose.

Thus for each (pixel) position in the image we

have: | ▽ f(x,y) | as the magnitude of the gradient

(R.Gonzales and R.Woods, 2001) on the edge map.

We normalize this value between 0 and 1 and will de-

note the normalized magnitude of gradient as g

′

. The

normalized edge map will be used as the input for our

algorithm.

3.2 Structure of Candidate Solutions

The convex shape C is represented as minimal set of

points making up the convex hull:

C = {(x

),...,(x

)} (1)

The points are represented by xy–coordinates of pix-

els in the edge map. n denotes the number of points

used to approximate the shape.

For C we aim to ﬁnd a convex shape with the largest

edge strength (as high as possible g

′

) in the edge map,

cf Figure 2.

Figure 2: An example edge map of a light microscope im-

age of the embryo of Emys orbicularis. C is denoted as a

red contour. Yellow dots are the points making up C.

The process of ﬁnding C is considered an optimiza-

tion problem; given a large number of candidate so-

lutions (shapes) we are trying to ﬁnd the optimal one.

For that reason an EA was a good candidate for a so-

lution.

When a solution (a contour) is found, the coordinates

of C are transferred to the initial image and the found

shape is cut out.

4 AN EA FOR CONVEX SHAPE

RECOGNITION

Evolutionary Algorithms (EA) (T.B¨ack, 1996) are

typically suitable for solving global optimization

problems (K.Deb, 2001), in particular when the solu-

tion space is very large and no straightforward analyt-

ical solution exists or can be found. In an EA, a popu-

lation of candidate solutions is evolved toward better

solutions by introducing computer analogues for re-

combination, mutation and selection.

The outline of a generic EA reads:

t = 0

Initialize P(t)

Evaluate P(t)

while not terminate do

P’(t) = SelectMates (P(t))

P’’(t) = Recombine (P’(t))

P’’’(t) = Mutate (P’’(t))

P(t + 1) = Select (P(t) \cup P’’’(t))

t = t + 1

end while

BIOINFORMATICS 2010 - International Conference on Bioinformatics

222

Here, t denotes the generation counter, P(t) =

,.. .,A

} is the population

of µ candidate solu-

tions (or individuals), and the functions SelectMates,

Recombine, Mutate, and Select represent the differ-

ent genetic operators. At the end of each iteration the

ﬁtness Φ(A(t + 1)) of each individual in the new pop-

ulation is generated and the individuals of P(t+1) are

sorted by their ﬁtness.

For the application of the principles of evolutionary

computation to the problem at hand one needs a suit-

able representation for the candidate solutions and a

method to determine the quality of the candidate so-

lutions which can serve as a ﬁtness function for the

optimization.

4.1 Individual Representation

An individual A is represented by a collection of

points (cf.3.2). Each point has a value which is the

normalized gradient g

′

(x,y) (cf.3.1). An individual

can be represented as a ﬁnite set of points on a planar

space:

A = {(x

),.. .,(x

)} (2)

The convex hull shape is determined by the boundary

points of a point collection. We will denote this col-

lection of convex boundary points C

for individual

. The subset of points in A

construct the convex

shape C

for individual j as shown in Figure 3. Thus

⊇ A

Figure 3: a) The representation of an individual A

as a col-

lection of points, b) an individual A

and its convex hull C

c) convex boundary points C

4.2 Genetic Operators

For this speciﬁc application we only use mutation.

For each individual the following applies: every point

in the individual is mutated with a probability p

mut

The general rule for the approximation of p

mut

is the

formula p

mut

= 1/l, where l is the length of a bit string

of properties of an individual; in our case the num-

ber of points of A. When mutation is applied to a

point (x,y) its coordinates are mutated within some

(small) mutation area O

mut

around the old position of

We use notation P, not for probability, but for the pop-

ulation in an EA as is done in (T.B¨ack, 1996).

the point. A mutation fails if the mutated pixel is out-

side the image of if g

′

(x,y) = 0 (there is no gradient

at all). Then O

mut

is enlarged enabling a more global

mutation.

4.3 Utility Function

The quality (or ﬁtness) of a candidate solution is com-

posed by the following:

1. i

is the fraction of all points of A which are

present on convex hull C:

|C|

|A|

→ max (3)

2. ¯g is the average gradient value of all points of A:

¯g =

∑

i=n

i=1

′

)

→ max (4)

3. b

is the normalized average gradient value of

points of the convex hull C (of individual A). We

calculate the average gradient value of the image

between these points. We perform a 8-connected

Bresenham-style walk (J.D.Foley et al., 1990) be-

tween all subsequent points in C. Let the func-

tion B((x

),(x

)) denote the average gradi-

ent value taken over the euclidean distance be-

tween consecutive points (x

) and (x

∑

i=i

−1

i=0

B((x

),(x

))

→ max (5)

4. σ

is the standard deviation of the convex hull

border segment length, normalized by the use of

average side distance. Let d((x

),(x

)) de-

note the euclidean distance between consecutive

points (x

) and (x

), d

avg

is the average dis-

tance of all these points.

= e

(−1.0/d

avg

)·

∑

i=i

−1

i=0

d((x

),(x

i+1

))−d

avg

→ max (6)

Since parameters (i

, ¯g,b

,σ

) need be optimized si-

multaneously we are looking at a multi-objective op-

timization problem. The objectives can be conﬂict-

ing, for example, increase of the points on convex

hull can lead to lower gradient values. In our ap-

proach we aggregate the multiple objective functions

into an univariate problem by making use of the con-

cept of Desirability Functions (DF) and Desirability

Index (DI) (D.Steuer, 1999). We also make use of a

simple DF where for each parameter i we make use of

a power function f(i) = i

(all parameters are in a nor-

malized representation, it remains in the interval [0,1]

for any exponent a. To combine the DF’s into one

overall quality value we use a aggregation of all the

parameters. The following product ﬁtness function is

parametrized as follows:

Φ(~a

(t)) = i

· ¯g

· b

· σ

→ max (7)

CONVEX SHAPE RETRIEVAL FROM EDGE MAPS BY THE USE OF AN EVOLUTIONARY ALGORITHM

223

4.4 Implementation

The number of points m in each individual can be set

depending on the precision of the prediction we want

to retrieve. Obviously a lower m gives less accurate

shape, while a higher m gives a more precise shape

but is computationaly more expensive.

The individuals are initialized with:

= U(0,ImageX), j = (1,.. .,n)

= U(0,ImageY), j = (1, ...,n) (8)

The convex shape C is calculated using the Graham

scan (R.L.Graham, 1972) algorithm with a time com-

plexity of O(m) (m is the number of points). Since the

algorithm needs a sorted list the points are sorted on

the x-coordinate by insertion sort.

Parent selection is repeated for each individual in the

new population (µ times). For the selection, tourna-

ment size q = 5 is chosen as one of the common set-

tings. A larger q results in less selective pressure. No

crossover is used, as it did not yield better results. As

a mutation rate of 1/m is most commonly used in EA,

the mutation rate for this implementation is chosen

accordingly, hence p

mut

= 1/m.

By means of empirical testing we found the following

settings ﬁt for our problem: a

= a

= 1, a

= 2, a

0.5.

5 EXPERIMENTS AND RESULTS

For all tests we use a standard gradient operator – the

Sobel (R.Gonzales and R.Woods, 2001) edge detector

for the edge map creation.

Figure 4: Snapshot of algorithm in search of best solution.

The process of ﬁnding the best solution is shown in

Figure 4. Thin yellow lines represent candidate solu-

tions. The bright red line represents the best solution

(with highest Φ).

5.1 Results: Finding a Convex Hull

Images from various ﬁelds in biology, containing con-

vex shapes were used for this test. The results are

shown in Table 1. As can be seen the shapes that

might be of interest are accurately retrieved. On

aIntel(R) Pentium(R) 4 CPU 3.2GHz this took on av-

erage 3 seconds.

Table 1: Some results of our algorithm applied to images

from different ﬁelds in biology after running for 70 genera-

tions and 2800 function–evaluations.

Input output input output

5.2 Results: Finding a Convex Hull

within a Convex Hull

In this section we will show that it is also possible to

retrieve a convex shape from another convex shape.

We have used and tested the approach for our par-

ticular data - images of zebraﬁsh in the early de-

velopment. The images were acquired using Leica

MZ16FA light microscope in 24-bit color at a resolu-

tion of 2592 × 1944 pixels. Time–lapse acquisition is

accomplished in automated fashion over time T(5 –

10h).

Figure 5: Zebraﬁsh embryo in early stage.

As can be seen in Figure 5 the shape of zebraﬁsh

embryos in early stages can be described as a de-

formed circle being the embryo (red shape in Figure

5), encapsulated in a larger (deformed) circle being

the membrane (yellow shape in Figure 5).

BIOINFORMATICS 2010 - International Conference on Bioinformatics

224

In our case to extract the embryo shape from the im-

age we run the convexhull extraction algorithm twice.

First are looking for the outer convex shape. The mo-

ment the approximation of the outer shape (the mem-

brane) is complexed we try to ﬁnd the inner shape

(the embryo), which is then the convexshape with the

largest edge strength within the membrane shape.

We have run the algorithm on a set of 600 images of

the zebraﬁsh embryo. A few results shown in Table

2. As can be seen the embryo shapes were retrieved

accurately. The algorithm failed in cases where the

edge map was very weak (out of focus), which was

2% of our test set. On an Intel(R) Pentium(R) 4 CPU

3.2GHz this took up to 10 seconds.

Table 2: Some results of our algorithm applied to images

of zebraﬁsh embryos after running for 300 generations and

24000 function–evaluations.

Input output Input images

6 DISCUSSION AND

CONCLUSION

In this paper, we have described the use of the EA for

the recognition of convex shaped objects and tested it

for different biological images.

We have demonstrated the application of the EA ap-

proach to different images and the possibility to re-

trieve both single convex shape (cf 5.1) as the possi-

bility to retrieve a convex shape from another convex

shape (cf 5.2).

In our approach the shape is not predeﬁned like in

most models based segmentation methods, but can be

any convex shape within an image (assuming there

is one convex shape in the image, we are looking

for). Also, our approach does not need a training

set like ASM does and can be used without signif-

icant changes for different applications within bio–

imaging.

The results are promising and our future direction is

to apply this strategy in high-throughput applications

for screening and compare it against other methods.

This form of fast automated image analysis is indis-

pensable for such approaches.

ACKNOWLEDGEMENTS

This work was supported by the Smartmix program of

the Netherlands Ministry of Economic Affairs. Spe-

cial thanks to G. Lamers for assistance with image

acquisition and L. Bertens for providing images.

REFERENCES

D.Steuer (1999). Multi-criteria-optimization and desirabil-

ity indices. Technical Report 20/99, University of

Dortmund, Statistics Department,.

F.J.Verbeek, D.D.Rodrigues, H.Spaink, and A.Siebes

(2004). Data submission of 3d image sets to a bio-

molecular database using active shape models and a

3d reference model for projection. Proceedings SPIE

/5304/, Internet Imaging V. 13-23.

F.Leymarie and M.D.Levine (1993). Tracking deformable

objects in the plane using an active contour model.

IEEE Transactions on Pattern Analysis and Machine

Intelligence. Vol. 15, No. 6.

J.A.Sethian and A.James (1999). Level set methods and fast

marching methods : Evolving interfaces in compu-

tational geometry, ﬂuid mechanics, computer vision,

and materials science. Cambridge University Press.

J.D.Foley, Dam, A., S.K.Feiner, and J.F.Hughes (1990).

Computer Graphics: Principles and Practice.

Addison-Wesley.

K.Deb (2001). Multi-Objective Optimization using Evolu-

tionary Algorithms. Wiley Interscience Series in sys-

tems and Optimization.

M.Kass, A.Witkin, and D.Terzopoulos (1987). Snakes: Ac-

tive contour models. International Journal of Com-

puter Vision. Vol. 1, No. 4.

R.Gonzales and R.Woods (2001). Digital Image Process-

ing. Addison-Wesley, London, 2nd edition.

R.L.Graham (1972). An efﬁcient algorithm for determining

the convex hull of a ﬁnite. Information Processing

Letters 1.

T.B¨ack (1996). Evolutionary Algorithms in Theory and

Practice: Evolution Strategies, Evolutionary Pro-

gramming, Genetic Algorithms. Oxford Univ. press.

T.F.Cootes, C.J.Taylor, D.H.Cooper, and J.Graham (2009).

Active shape models - their training and application.

Computer Vision and Image Understanding, Vol. 61,

No. 1.

Y.N.Wu, Z.Si, C.Fleming, and Zhu, S. (2007). Deformable

template. IEEE International Conference on Com-

puter Vision.

CONVEX SHAPE RETRIEVAL FROM EDGE MAPS BY THE USE OF AN EVOLUTIONARY ALGORITHM

225