ARCHITECTURE FOR HUMAN-ROBOT COLLABORATIVE

NAVIGATION

Sousso Kelouwani, Patrice Boucher and Paul Cohen

Ecole Polytechnique, 2900, boul.

Edouard-Montpetit Campus de l’Universit

e de Montr

eal, Montr

eal (Qu

ebec), Canada

Keywords:

Motorized wheelchair, Robotic architecture, Shared control, Three-layer architecture, Collaborative control.

Abstract:

Various situations of mobile platform navigation controls require a collaboration between a human agent and

autonomous navigation modules. This work presents a new approach for collaborative control between such

two agents, based upon a three-layer architecture. An arbitration scheme is proposed in the deliberative layer

as well as a collaborative planning method for trajectory following based upon optimal control theory in the

sequencer layer. The collaborative control signal in the execution layer is a weighted summation of each

agent control signal. This collaborative architecture could be used for the shared control of vehicles such as

motorized wheelchairs. Experimental results illustrate the efﬁciency of the proposed control architecture.

1 INTRODUCTION

The shared control of a robotic platform falls into

two categories: the ﬁrst one corresponds to situations

where the various agents compete to ﬁnd the best con-

trol action to be selected and applied (Skrzypczyk,

2005). The second category corresponds to a col-

laborative approach aiming at achieving a given goal

(S. Katsura, 2004; Q. Zeng, 2008; C. Urdiales and

Sandoval, 2007). This paper focuses on a collabo-

rative approach to shared control between a human

agent onboard a mobile platform, such as a motor-

ized wheelchair for example, and an autonomous nav-

igation module. The autonomous navigation module

relies on its proximity sensors (sonar, infrared, laser

range ﬁnder, etc.) in order to perform the naviga-

tion task; its ability to sense the surrounding envi-

ronment is therefore, limited by its perception and

interpretation capabilities. Based upon its own sen-

sory system, the human agent can contribute to ex-

tend the autonomous module capabilities by provid-

ing a control signal that allows the platform to avoid

non-detected dangers and improve its navigation per-

formance. Inversely, in situations where human per-

ception and control suffer momentarily from a lack of

attention, the autonomous navigation module may be

able to compensate and avoid imminent dangers. Fur-

thermore, various types of maneuvers in constrained

environments, such as doorway passing or parking,

may exceed the human agent capabilities and require

the help of the autonomous agent.

Previous work on collaborative navigation control fo-

cused on the decision problem (A. Huntemann and

al., 2007; T. Taha and Dissanayake, 2007; Y. Qi and

Huang, 2008; T. Okawa and Yamaguchi, 2007) (i.e.

the determination of the navigation task), while the

planning aspect, i.e. the determination of the se-

quence of platform actions that may be used) is left

to the responsibility of the Autonomous Navigation

Module (C. Urdiales and Sandoval, 2007; Q. Zeng,

2008). Usually, there are more than one sequence

of platform actions that can be used to reach a given

goal and the one selected by the Autonomous Naviga-

tion Module is not necessarily what the Human agent

would do if he was responsible of the planning. This

paper presents two contributions: the ﬁrst one con-

sists of a reactive arbitration scheme that allows two

agents with different perception modalities to avoid

perceived obstacles. The second contribution consists

of a collaborative architecture that efﬁciently includes

both agents control signals at decision and planning

levels. In addition, we provide a formal approach to

the integration of the Human Agent plan during the

elaboration of the Autonomous Navigation Module

plan. This method is based upon the multi-agent op-

timal control theory (Cruz, 1978; Simaan and Cruz,

1973; Y. C. Ho and Olsder, 1982).

The rest of the paper is organised into 4 sections.

Section 2 presents the deliberative obstacle avoidance

scheme. In section 3, the collaborative architecture is

316

Kelouwani S., Boucher P. and Cohen P. (2010).

ARCHITECTURE FOR HUMAN-ROBOT COLLABORATIVE NAVIGATION.

In Proceedings of the Third International Conference on Health Informatics, pages 316-323

DOI: 10.5220/0002745403160323

 SciTePress

discussed. Experimentations and conclusion are pre-

sented in section 4 and section 5, respectively.

2 OBSTACLE AVOIDANCE

DELIBERATIVE APPROACH

2.1 Problem Statement

The main goal of this work is to design a system that

can allow a Human Agent (HA) and an Autonomous

Navigation Module (ANM) to collaborate during nav-

igation tasks of a mobile platform. Given an envi-

ronment map and the current mobile platform con-

ﬁguration (position and orientation), the ANM agent

aims at helping the HA to reach a given destination

without colliding with obstacles, as perceived by the

ANM. The help mentioned here is related to the fact

that the ANM agent is continuously supervising the

HA control signal and intervenes only to avoid colli-

sions. Since the two agents perception systems differ,

various situations may occur in which:

• a danger is perceptible by the ANM agent alone:

we designate by S

the set of such events; nav-

igation control priority should be given to the

ANM;

• a danger is perceptible by the Human agent alone:

we designate by S

the set of such events; naviga-

tion control priority should be left to the HA;

• a danger is perceptible by both agents: we des-

ignate by S

ham

the set of such events; navigation

control should be based upon deliberation;

• a danger is not perceptible by any of the two

agents; a collision is unavoidable.

The main problem consists in establishing an arbi-

tration scheme that will produce the desired decision

scheme outlined above.

2.2 Preliminary Considerations

We assume that, at the beginning of the navigation

task, a map of the environment and the destination

conﬁguration are available to the ANM. At each step

k, each of the two agents provides a control signal

based upon their current perception of the environ-

ment. From the perspective of the arbitration scheme

to be designed, a control signal is considered to be

safe if its application does not lead to collision for an

obstacle belonging to S

or S

ham

We designate by U

(k) and U

(k) HA and the ANM

control signals respectively. Since both agents are not

competing, a reasonable choice for the collaborative

control signal consists of selecting a weighted sum of

both signals U

(k) and U

(k). The agent with higher

priority will have the largest control signal weight.

Solving the deliberation problem is equivalent to ﬁnd-

ing the weight relative to each agent. For simplicity,

we designate these weights by α(k) and (1 − α(k))

with α(k) ∈ [0, 1] where α(k) is the ANM control sig-

nal weight at step k. The following expression corre-

sponds to the collaborative control signal U (k):

U(k) = (1 − α(k))U

(k) + α(k)U

(k) (1)

Given U

(k) and U

(k), the deliberative control prob-

lem consists of determining the value of α(k) at each

step k.

2.3 Approach for Solving the

Deliberative Problem

The precedence of U

over U

must be taken into ac-

count when solving the above problem. Indeed, the

ANM should not generate its control signal without

taking into account the motion direction implied by

the HA control signal. This constraint is important in

order to allow the platform to follow the HA control

signal whenever several ways exist to safely achieve

a maneuver. For example, in front of an obstacle be-

longing to S

ham

, the HA decision on how to avoid it

must be complied with. Similarly, in the absence of

any danger, the ANM should generate a control sig-

nal U

close to U

since there is no need to help the

human agent in such a situation.

A criterion, called non-collision index P(k) ∈ [0, 1],

must be deﬁned in order to allow the arbitration

scheme to assess the risk of a collision if one of the

two control signals were to be used alone. P(k) should

be small if a collision is likely to happen. The follow-

ing expression is a good candidate to represent the

non-collision index:

P(k) = e

−C

min

(k)

(2)

where d

min

(k) > 0 represents the minimum dis-

tance between the platform position and the nearest

obstacle in the direction of motion. The value of the

index decreasing rate C depends upon the navigation

context. Given the expression of P(k), we deﬁne the

Human agent non-collision index P

(k) and the ANM

non-collision index P

(k) as:

(k) = e

−C

min

(k)

(3)

(k) = e

−C

min

(k)

(4)

where d

min

(k) > 0 represents the minimum distance

between the platform conﬁguration and the nearest

ARCHITECTURE FOR HUMAN-ROBOT COLLABORATIVE NAVIGATION

317

obstacle if only U

(k) was applied and d

min

(k) > 0

represents the corresponding distance if only U

(k)

was applied. Given P

(k) and P

(k), the value of α(k)

is derived as:

α(k) =

(k)

(k) + P

(k)

(5)

Arbitration Scheme Description

The arbitration scheme has two phases: the supervi-

sion phase and the correction phase. Let us deﬁne P

as a minimum predeﬁned non-collision index. The

system is in the supervision phase if P

(k) > P

. Oth-

erwise, the system is in the correction phase.

Supervision Phase:

During this phase and at each step, the deliberative

module computes P

(k). If U

(k) leads to a safe mo-

tion, the following condition holds: P

(k) > P

. The

ANM generates U

(k) close to U

(k) since there is no

need to help the human agent. But the deliberative

module will set α(k) to 0 so that U(k) is exactly equal

to U

(k) according to equation 1. Therefore, the plat-

form is under the control of the human agent.

Correction Phase:

When P

(k) <= P

, a collision may happen if U

(k)

is applied directly. Perceiving the obstacle, as part

of S

or S

ham

, the ANM generates a control sig-

nal U

(k) in order to avoid collision. Since U

(k) is

safer than U

(k), the non-collision index P

(k) will be

greater than P

(k). According to equation 5, the value

of α(k) is greater than 0.5, allowing a greater contri-

bution of the ANM control signal into the collabora-

tive control signal. In the extreme case when U

(k) is

very unsafe, α(k) will be close to 1 and the collabora-

tive control signal U (k) will be close to U

(k).

On the basis of this arbitration scheme, the collabora-

tive control system will behave as speciﬁed in Section

2.1.

2.4 Limitation of the Arbitration

Scheme

The proposed arbitration handles correctly the three

cases mentioned Section 2.1. However, since the list

of cases was not exhaustive, the arbitration scheme

may not correctly avoid all situations of collisions.

For example, an obstacle belonging to S

on the left

of the platform and a second one belonging to S

in front of it, while the platform is moving straight-

forward, may cause the ANM to generate a control

signal U

(k) that will induce a motion on the left, thus

leading to a collision.

The next section presents a complete collaborative ar-

chitecture designed to test the proposed arbitration

scheme.

3 COLLABORATIVE

NAVIGATION ARCHITECTURE

The subsumption (Brooks, 1986) and the three-layer

architectures (E. Gat and Murphy, 1998) are among

well-known robotic architectures used for platform

navigation applications. The subsumption archi-

tecture is associated with reactive behaviour-based

robots. Since upper layers interfere with lower layers,

they cannot be designed independently. The three-

layer architecture consists of a Deliberative Layer for

navigation task selection, a Sequencer Layer for re-

active planning and an Execution Layer for low level

effector control. Due to its modular concept, we select

the three layer architecture as the basis of the collab-

orative control architecture presented here. This col-

laborative architecture has the advantage of providing

a high level of decoupling between layers, each layer

(deliberative, sequencer or execution layer) can be de-

signed without attention to the roles of the other layers

of the architecture.

Figure 1: Collaborative Architecture for Navigation.

3.1 Deliberative Layer

The Deliberative Layer is the top layer of the pro-

posed architecture. It has the core of the ANM and

the Mediation module.

3.1.1 Autonomous Navigation Module

The role of this module is to provide at each step k a

control signal U

(k) that leads to safe motion. When

HEALTHINF 2010 - International Conference on Health Informatics

318

an obstacle is perceived, it uses a collision avoidance

algorithm based upon the Virtual Field Histogram ap-

proach (VFH) (Borenstein and Koren, 1991). Fig-

ure 2 illustrates how the ANM control signal can be

generated using a VFH based obstacle avoidance ap-

proach.

Figure 2: Trajectory Generation: At step k, the platform

receives the control signal from each agent. If the Human

control signal is applied alone, the platform conﬁguration at

step k + 1 will be X

(k + 1). If the Autonomous Navigation

Module control signal is applied alone, the platform con-

ﬁguration at step k + 1 will be X

(k + 1). By applying both

control signals at step k, the next platform conﬁguration will

be between X

(k +1) and X

(k +1). This conﬁguration will

be close to X

(k + 1) and X

(k + 1) is close to 1.

Assume that X

= [x

]

is the platform des-

tination conﬁguration and X(k) = [x(k) y(k) θ(k)]

the current platform conﬁguration as shown in Fig-

ure 2. Based upon X(k), X

and obstacles around the

platform, the Virtual Field Histogram (VFH) method

is used to ﬁnd the lowest obstacle density direction

for platform move (Borenstein and Koren, 1991).

This direction is called the VFH direction and deﬁnes

the orientation θ

(k + 1). In order to ﬁnd the point

(k + 1), y

(k + 1)) on that direction, we propose a

method that will allow the human agent to move and

stop the platform at will.

At step k, the HA provides its control signal U

(k). If

(k) is applied without any contribution of the ANM

agent control signal, the platform conﬁguration will

be X

(k + 1) = [x

(k + 1) y

(k + 1) θ

(k + 1)]

. The

point (x

(k), y

(k)) is selected on the VFH direction

so that the Euclidian distance between (x(k), y(k))

and (x

(k + 1), y

(k + 1)) is the same as that between

(x(k), y(k)) and (x

(k + 1), y

(k + 1)).

3.1.2 Mediator Module

This module uses the arbitration scheme presented in

section 2.3 in order to produce the collaborative con-

trol signal U(k).

3.2 Collaborative Sequencer Layer

The HA control signal can be affected by variations

originating from the input modality uncertainty or

hand tremors. In this section, we propose an ap-

proach that signiﬁcantly reduces the impact of un-

wanted variations on the collaborative control. In or-

der to present our method, let us consider the signal

control diagram shown in Figure 3.

Figure 3: Control Signal Diagram. The individual appli-

cation of U

(k) and U

(k) will produce the conﬁguration

(k +1) and X

(k +1) respectively. However, due to α(k),

the collaborative control signal U(k) will produce X (k + 1).

Given the value of α(k), there are two ways to

compute the collaborative control signal U(k) shown

in Figure 3:

U(k) = α(k)U

(k) + (1 − α(k))U

(k) (6)

U(k) = U

(k) +U

(k) (7)

According to equation 6 and knowing that the U

(k)

is independent from U

(k), we get:

∂U (k)

∂U

(k)

= (1 − α(k))I (8)

where I is a (3×3) identity matrix. On the other hand,

according to equation 7:

∂U (k)

∂U

(k)

∂U

(k)

∂U

(k)

+ I (9)

If U

(k) is selected so that

∂U

(k)

∂U

(k)

< −α(k)I (10)

then the second way for computing U(k) is more ef-

ﬁcient than the ﬁrst method represented by equation

6. We provide a method based on the optimal control

theory that allows to select U

(k).

Recall that the role of the Sequencer Layer is to pro-

vide U

(k) given X(k), X (k + 1) and the dynamic

model of the platform. If the Execution Layer has

enough time to move the platform from X(k) to X(k+

ARCHITECTURE FOR HUMAN-ROBOT COLLABORATIVE NAVIGATION

319

1), given the control signal U(k), then its dynamic be-

havior can be approximated by the following linear

equation:

X(k + 1) = X(k) +U(k) (11)

where U(k) is represented by equation 7. In col-

laborative navigation contexts such as motorized

wheelchair control, it is useful to constrain U

(k) in

order to ensure smooth behavior. Large magnitudes

of U

(k) should be avoided and the deviation between

platform conﬁgurations X(k) and the X

(k) should be

minimized in order to allow the platform to follow the

sequence of X

. The following functional expression

takes into account the above mentioned requirements.

(k)] =

M−1

∑

k=0

(k) +

(M) (12)

where:

(k) = [X(k) − X

(k + 1)]

(k)[X(k) − X

(k + 1)]

(k)R

(k)U

(k)

(13)

(M) = [X(M) − X

(M + 1)]

(M)[X(M) − X

(M + 1)]

(14)

(k) is a (3 × 3) symmetric and positive semi-

deﬁnite matrix that penalizes the deviation between

the platform conﬁguration and the mediated conﬁgu-

ration at step k;

(k) is a (3× 3) symmetric and positive deﬁnite ma-

trix that penalizes large sequencer control signals at

step k.

The optimal sequence {U

∗

(k), k = 0, ..., M − 1} is,

therefore, the sequence {U

(k), k = 0, ..., M − 1} that

minimizes the functional expression 12 under the con-

straint 11.

3.2.1 Solving the Planning Problem

In order to solve the optimization problem, we as-

sume that the state vector is fully accessible to the

sequencer and that the initial state vector X(0) is

completely known. Furthermore, we consider that

(k), k = 0, ..., M − 1 is known. Using the Hamilto-

nian calculus (Lewis and Syrmos, 2005), we obtained:

∗

(k) = F

(k)X(k) + F

(k)U

(k) + F

(k)V (k + 1)

(15)

where:

(k) = −R

−1

(k)S(k + 1)F(k) (16)

F(k) = [I + R

−1

(k)S(k + 1)] (17)

(k) = −R

−1

(k)S(k + 1)F(k) (18)

(k) = R

−1

(k)[I − S(k + 1)F(k)R

−1

(k)] (19)

S(k) = S(k + 1)F(k) + Q

(k) (20)

V (k) = Q

(k)X

(k + 1) +V (k + 1)

+S(k + 1)F(k)R

−1

(k)V (k + 1)

−S(k + 1)F(k)U

(k) (21)

According to equation 7, the collaborative control sig-

nal is given by:

U(k) = U

∗

(k) +U

(k)

In order to reduce variations on U

(k), the values of

(k) and Q

(k) are selected so that the following

condition holds:

∂U

∗

(k)

∂U

(k)

< −α(k)I (22)

3.3 Execution Layer

We assume that the robotic platform conﬁguration

X(k) at step k is represented by its conﬁguration ex-

pressed in a reference frame (working space). The

Execution Layer, in the three-layer architecture, is de-

signed to be tightly coupled with sensors and actua-

tors. It receives a set point (or a target conﬁguration)

and, through the use of one or more control loops,

tries to reach that point. However, in the proposed

collaborative architecture, the Execution Layer input

signal U(k) is a weighted sum of two control signals.

Based upon the platform dynamic equation, the cur-

rent conﬁguration and U(k), the next conﬁguration

is computed and used as a set point for the Position

Controller which is part of the Execution Layer. The

Position Controller needs to ﬁnd a control law that

minimizes the deviation between the conﬁguration

obtained by applying the control law and the given

conﬁguration. Many methods exist to solve the con-

troller problem in the case of a mobile platform (As-

tolﬁ, 1999), (Y. Kanayama and Noguchi, 1990). Re-

cently, Belkhous (S. Belkhous and Nerguizian, 2005)

proposed a new method based on Lyapunov theory.

Since the Execution Layer is decoupled with the up-

per layers, any other platform dynamic model can be

used with a minimum architecture modiﬁcation.

4 EXPERIMENTS

4.1 Experimental Setup

In order to test the proposed arbitration scheme and

the collaborative architecture, a ﬁrst test scenario rep-

resented in Figure 4 is used on a mobile robotic

platform. Starting from a rest position at A(0, 0),

HEALTHINF 2010 - International Conference on Health Informatics

320

the ANM and the HA must collaborate in order to

drive the platform to the destination point E(7, 0)),

by avoiding obstacles along the way. A negative ob-

stacle is at position B(1.5, 0) and a positive obstacle

is at C(3.5, 0). Furthermore, the platform must pass

through a doorway at position D(6.2, 0) before reach-

ing destination point E. The platform has one on-

board laser range ﬁnder for obstacle detection. Due

to the ranger ﬁnder position on the platform, negative

obstacles cannot be detected. On the other hand, we

assume that the HA is capable of perceiving negative

obstacles, therefore, belonging to set S

. For illustra-

tion purposes, we assume that the positive obstacle at

position C is only perceived by the ANM through its

range ﬁnder. Both agents can perceive the doorway.

Hence, the positive obstacle belongs to set S

and

the doorframe belongs to set S

ham

The second scenario intends to illustrate the collabo-

ration when the obstacle belongs to S

ham

. This sce-

nario is represented in Figure 5. The mobile platform

must move forward for about 1 meter, turn in order to

face the doorframe and then move through the door-

way. The doorway opening is 65cm wide, whereas

the mobile platform width is 55cm.

Figure 4: Navigation Scenario.

Figure 5: Doorway Passing Setup.

The mobile platform used for experiments is an

ATRV-Mini manufactured by IRobot, equipped with

a SICK laser rangeﬁnder, model LMS200. Player-

Stage (H. J. Toby and al., 2005) and Acropolis (Zalzal

and al., 2006) softwares were used for the implemen-

tation. A standard joystick was used as the human

agent input modality. The planning horizon of the se-

quencer layer is set to 1 and all involved matrices are

set to the identity matrix I, except for R

(k) which is

set to 10

−3

4.2 Experience 1: Navigation with

Obstacle Avoidance

Figure 6 shows three examples of trajectories. The

ﬁrst trajectory (grey curve) represents the Human

agent trajectory, if he was alone to drive the platform.

The second trajectory (dashed curve) represents the

ANM trajectory when the signal of the HA is not

taken into account. The third trajectory (continuous

black curve) is the collaborative trajectory when both

agents are participating. In this case, the collaborative

trajectory shows that the platform was able to reach

the destination while avoiding the positive and nega-

tive obstacles.

Figure 7 shows that during the negative obstacle

avoidance, the ANM contribution was small, and the

HA was able to avoid it without ANM control signal

interference. α becomes close to 1 during the positive

obstacle avoidance phase, the platform being able to

avoid it despite the presence of the Human agent con-

trol signal.

Figure 6: Example of Navigation Trajectories.

4.3 Experience 2: Doorway Passing

Figure 8 represents the evolution of α during the door-

way traversing experiment. As one can notice, the

contribution of the ANM changes in order to compen-

sate for non safe HA control signals. Ten trials were

performed and the platform was able to pass through

the doorway.

ARCHITECTURE FOR HUMAN-ROBOT COLLABORATIVE NAVIGATION

321

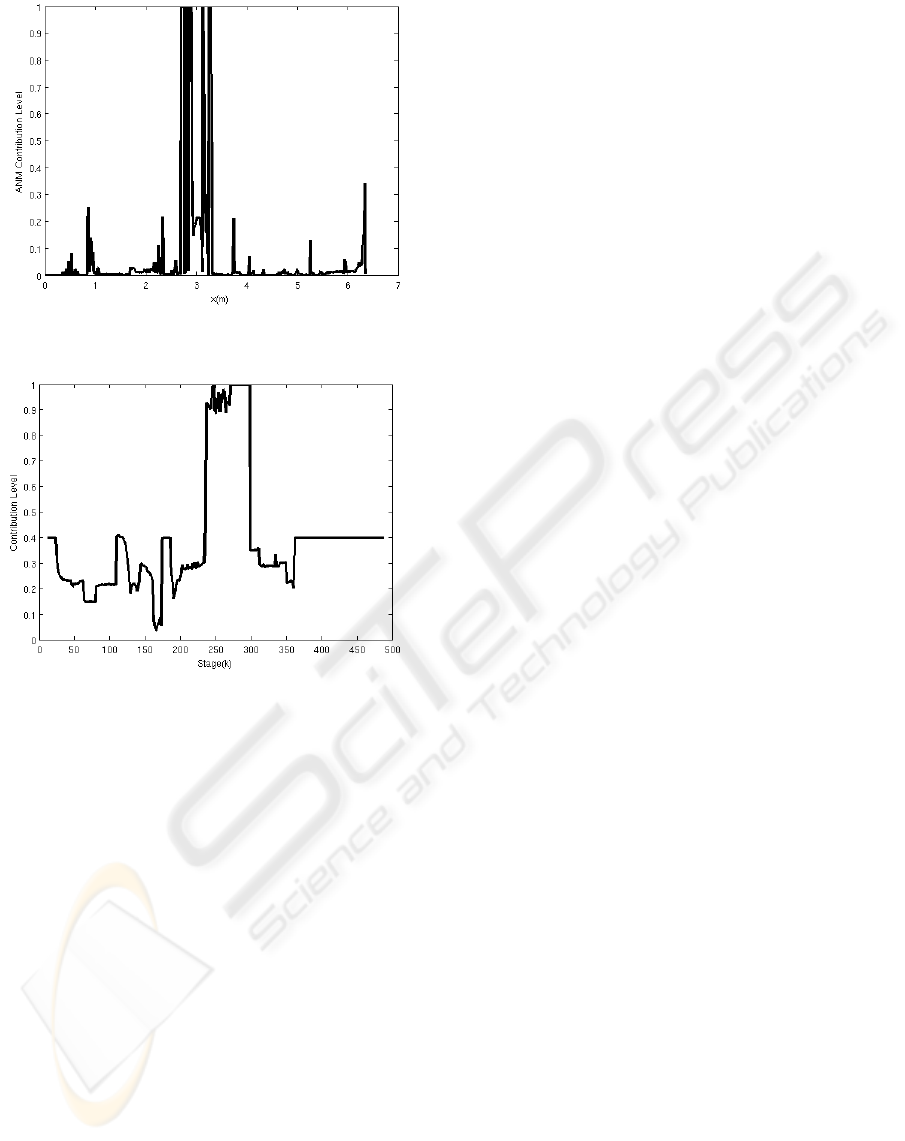
Figure 7: Collaborative Control: ANM Contribution Level

α while the platform is moving on the x − axis.

Figure 8: Dynamic Evolution of al pha during doorway

traversing experiment.

5 CONCLUSIONS

A robotic architecture that allows a human agent and

an autonomous navigation module agent to collabo-

rate during navigation tasks was proposed. This ar-

chitecture has three layers, namely deliberative, se-

quencing and execution layers. In order to build the

deliberative layer, an arbritage scheme based upon

the value of a non-collision index is used. In the se-

quencer layer, both agents control signals are taken

into account. Experiments performed with a mobile

platform show that this architecture and its arbitration

scheme can be used in robotic application in order to

enhance a human agent obstacle avoidance capabil-

ity. Applications such as powered wheelchair driving

could use the proposed architecture.

ACKNOWLEDGEMENTS

This work has been supported by the Natural Science

and Engineering Research Council of Canada (Grant

No CRD 349481-06 and Scholarship No BESC D3-

348674-2007). The authors wish to tank Hai Nguyen,

Vincent Zalzal, Raphael Gava and Alexandre Fortin

from the Perception and Robotics Laboratory of Ecole

Polytechnique for their contributions in implementa-

tion and testing.

REFERENCES

A. Huntemann, E. D. and al. (2007). Bayesian plan recog-

nition and shared control under uncertainty: Assist-

ing wheelchair drivers by tracking ﬁne motion paths.

In International Conference on Intelligent Robots and

Systems. San Diego, CA, United States.

Astolﬁ, A. (1999). Exponential stabilization of a wheeled

mobile robot via discontinuous control. In Journal of

Dynamic Systems, Measurement, and Control.

Borenstein, J. and Koren, Y. (1991). The vector ﬁeld

histogram-fast obstacle avoidance for mobilerobots.

In IEEE Transactions on Robotics and Automation.

Brooks, R. A. (1986). A robust layered control system for

a mobile robot. In IEEE Journal on Robotics and Au-

tomation.

C. Urdiales, A. Poncela, I. S.-T. F. G. M. O. and Sandoval,

F. (2007). Efﬁciency based reactive shared control

for collaborative human/robot navigation. In Interna-

tional Conference on Intelligent Robots and Systems.

San Diego, CA, USA.

Cruz, J. B. (1978). Leader-follower strategies for multilevel

systems. In IEEE Transactions on Automatic Control.

E. Gat, R. P. B. and Murphy, R. (1998). On three-layer

architectures. In Artiﬁcial Intelligence and Mobile

Robots.

H. J. Toby, C. and al. (2005). Player 2.0: Toward a practical

robot programming framework,. In Australasian Con-

ference on Robotics and Automation. Sydney, Aus-

tralia.

Lewis, F. and Syrmos, V. (2005). Optimal control. New

York, John Willey & Son.

Q. Zeng, B. Rebsamen, E. B.-L. C. (2008). A collaborative

wheelchair system. In IEEE Transactions on Neural

Systems and Rehabilitation Engineering.

S. Belkhous, A. Azzouzi, M. S.-C. N. and Nerguizian, V.

(2005). A novel approach for mobile robot naviga-

tion with dynamic obstacles avoidance. In Journal of

Intelligent and Robotic Systems.

S. Katsura, K. O. (2004). Human collaborative wheelchair

for haptic interaction based on dual compliance con-

trol. In IEEE Transactions on Industrial Electronics.

Simaan, M. and Cruz, J. B. (1973). On the stackelberg strat-

egy in nonzero-sum games. In Journal of Optimiza-

tion Theory and Applications.

HEALTHINF 2010 - International Conference on Health Informatics

322

Skrzypczyk, K. (2005). Control of a team of mobile robots

based on non-ccoperative equilibra with partial co-

ordination. In International Journal Applied Mathe-

matic Computer Science.

T. Okawa, E. S. and Yamaguchi, T. (2007). Information sup-

port system with case-based reasoning using motion

recognition in human-centered city. In SICE Annual

Conference. Takamatsu, Japan.

T. Taha, J. M. and Dissanayake, G. (2007). Wheelchair

driver assistance and intention prediction using

pomdps. In International Conference on Intelligent

Sensors, Sensor Networks and Information Process-

ing. Melbourne, VIC, Australia.

Y. C. Ho, P. L. and Olsder, G. (1982). Control-theoretic

view on incentives. In Automatica.

Y. Kanayama, K. Yoshihiko, F. M. and Noguchi, T. (1990).

A stable tracking control method for an autonomous

mobile robot. In IEEE International Conference

Robotics and Automation.

Y. Qi, Z. W. and Huang, Y. (2008). A non-contact eye-

gaze tracking system for human computer interaction.

In International Conference on Wavelet Analysis and

Pattern Recognition. Beijing, China.

Zalzal, V. and al. (2006). Mutual localization of mobile

robotic platforms using kalman ﬁltering. In IEEE In-

dustrial Electronics Conference.

ARCHITECTURE FOR HUMAN-ROBOT COLLABORATIVE NAVIGATION

323