AN INTELLIGENT SUPPORT SYSTEM FOR DIABETIC

PATIENTS

Mark Hoogendoorn, Michel C. A. Klein and Nataliya M. Mogles

VU University Amsterdam, Department of Artificial Intelligence, De Boelelaan 1081, Amsterdam, Netherlands

Keywords: Diabetes, Model-based reasoning, Intelligent support.

Abstract: Diabetes Mellitus type I is a disease that forces patients to manage their blood glucose level manually, by

balancing their activities, food intake and insulin dosages. There is a large experience with building

computational models for blood glucose level in diabetic patients, which are primarily used to design the

medication regime for a specific patient. In this paper, the design of an intelligent support application is

presented that uses a standard model for blood glucose level to give patients real-time advice about insulin

and food intake. The advice is based on measurements of blood glucose level, the electronic agenda of a

patient and model-based predictions of the glucose level in the near future. A simulation of the application

is presented that illustrates the feasibility of the system.

1 INTRODUCTION

Diabetes mellitus is a syndrome that is characterized

by dysfunctional metabolism, resulting in too high

blood sugar levels. According to the World Health

Organization, the prevalence of diabetes for all age-

groups worldwide is estimated to be 2.8% in 2000

and 4.4% in 2030. The total number of people with

diabetes is projected to rise from 171 million in 2000

to 366 million in 2030 (Wild et al, 2000).

The glucose level in humans is regulated by a

mechanism that is composed of several interacting

systems, in which the hormone insulin is the very

important, as it decreases the blood glucose level.

There are two types of diabetic patients: in type 1

patients, the high blood glucose levels are caused by

the loss of the insulin-producing cells in the

pancreas, in type 2 patients the body developed a

reduced sensitivity (or even resistance) to insulin.

Diabetes mellitus is currently a chronic disease,

without a cure, and is treated by a combination of

dietary guidelines, exercises and insulin

supplementation. The main challenge for diabetes

patients is to manually keep their blood glucose

level within a safe range, by balancing both their

glucose intake, their physical activities as their

insulin dosages (note that type II patients are not

always treated with insulin). This management is

complicated and a burdensome task for diabetic

patients. Specifically, the following reasons are

mentioned (Wikipedia, 2009):

1. The glucose cycle is a system which is affected

by two factors: entry of glucose into the

bloodstream and also blood levels of insulin to

control its transport out of the bloodstream;

2. As a system, it is sensitive to diet and exercise;

3. It is affected by the need for user anticipation

due to the complicating effects of time delays

between any activity and the respective impact

on the glucose system;

4. Management is highly intrusive and

compliance is an issue, since it relies upon user

lifestyle change and (often) upon regular

sampling and measuring of blood glucose

levels, multiple times a day in many cases;

5. It changes as people grow and develop;

6. It is highly individual.

In this paper, we investigate the options for an

intelligent support system that helps diabetic patients

controlling their blood glucose, exploiting

measurements via sensor devices, information about

activity from electronic agenda’s and model-based

predictions of the blood glucose level. One of the

features of such a system could be automated tuning

of the model parameters to an individual patient.

Together, such a system would ease the management

of diabetes for patients in several aspects. The usage

of a glucose-insulin model automates the assessment

of the interaction of the different factors (complexity

1 & 2 in the list above), the prediction and usage of

Hoogendoorn M., Klein M. and Mogles N. (2010).

AN INTELLIGENT SUPPORT SYSTEM FOR DIABETIC PATIENTS.

In Proceedings of the Third International Conference on Health Informatics, pages 98-105

DOI: 10.5220/0002747600980105

 SciTePress

electronic agenda information automates part of the

anticipation (number 3 in the list), while parameter

tuning allows for personalization and adaptation

over time (complexity 5 & 6).

In the next Section, we describe the main factors

of blood glucose regulation process in the human

body and a mathematical model that is often used for

describing the glucose-insulin interaction. Section 3

sketches the main elements of an intelligent support

system using the glucose model and sensor

measurements. In Section 4 we show a number of

simulations of patients with different activity

patterns and the effect of an intelligent support

system consisting of the components described in

the section before. Finally, Section 5 concludes the

paper.

2 MODELING BLOOD GLUCOSE

LEVEL

Mathematical or computational models of diabetes

type I have been under development for several

decades (see e.g. Bolie, 1961, Ackerman, 1965,

Sorensen, 1985, Puckett, 1992, and Leaning and

Boroujerdi, 1991). Models range from ordinary

systems of differential equations to stochastic

differential equations. Makroglou et al present a nice

overview of the various types of models that exist.

Within the ordinary systems of differential

equations, the model used most frequently is the so-

called minimal model which has been introduced by

Bergman. The development of the model has been

motivated by a desire to model the intravenous

glucose tolerance test. Such models consist of many

parameters that are very specific towards patients.

As a result, parameter estimation techniques have

been proposed that allow the tailoring of the models

towards the patients. In (De Geatano and Arino) the

results of one of such parameter estimation

techniques are shown, namely a quasi-Newton

minimization algorithm.

In this paper, the minimal model as introduced

by Bergman et al (1979; Tololo et al 1980) is

adopted. The model consists of the following three

formulas:

dG(t)/dt = – [p

+ X(t)]G(t) + p

(1a)

= – X(t)G(t) + p

– G(t)] (1b)

dX(t)/dt = – p

X(t) + p

[I(t) – I

]

(2)

dI(t)/dt = p

[G(t) – p

]

t – p

[I(t) – I

] (3)

In this formula, G(t) is the blood glucose

concentration, I(t) is the blood insulin concentration,

and X(t) is related to the interstitial insulin level, i.e.

the insulin that is at a location where it can actually

effect the glucose uptake by cells. Furthermore,

• G

is the subject's baseline glucose level;

• I

is the subject's baseline insulin level;

• p

is the glucose “mass action” rate constant, i.e.

the insulin-independent rate constant of tissue

glucose uptake;

• p

is the rate constant expressing the spontaneous

decrease of tissue glucose uptake ability;

• p

is the insulin-dependent increase in tissue

glucose uptake ability;

• p

is the rate of pancreatic release of insulin after

glucose intake;

• p

is the pancreatic “target” blood sugar level;

• p

is the decay rate constant for insulin in plasma;

For patients with diabetes type 1, we assume that the

pancreas does not produce any insulin anymore. In

the model, the effect is that parameters p

and I

are

zero. Consequently, the insulin level is determined

only by the artificial intake of insulin and the decay,

with I

(t)denoting the artificial insulin supply at

certain time points:

dI(t)/dt = – p

[I(t)] + I

(t) (4)

The minimal model does not take the effect of

physical effort into account. The effect of physical

effort on the insulin and the blood glucose balance is

twofold:

• it increases the insulin use by cells;

• it lowers the glucose concentration during and

after the exercise (Goodyear and Kahn, 1998).

Especially the fact that the glucose concentration is

also lowered after the exercise (up to 24 hours) is an

important factor to take into account. According to

(Derouich and Boutayeb, 2002), the minimal model

extended with the effect of exercises can be

described by the following formulas:

dG(t)/dt = – [1 + q

] X(t)G(t) + [p

+ q

][G

– G(t)] (5)

dX(t)/dt = – p

X(t) + [p

+ q

][I(t) – I

] (6)

In these formulae, the q-parameters define the effect

of physical activity. They are defined as follows:

• q

: the effect of the physical exercise in

accelerating the utilization of glucose by muscles

and the liver.

• q

: the effect of the physical exercise in

increasing the muscular and liver sensibility to

the action of the insulin.

AN INTELLIGENT SUPPORT SYSTEM FOR DIABETIC PATIENTS

• q

: the effect of the physical exercise in

increasing the utilization of the insulin.

The q

variable is also larger then 0 for some time

after the exercise.

3 INTELLIGENT SUPPORT

Currently, diabetes patients design a schema for

insulin intake in consultation with their medical

practitioner. This schema is based on a registration

of regular blood glucose measurements. Patients will

also use their common sense knowledge about the

effect of their activities on their blood glucose level:

for example, if a large meal is consumed, the person

will take a somewhat higher dose of insulin, or if

sporting activities are planned, some additional food

(especially) carbohydrates will be taken. In addition

to this, patients will do regular blood glucose

measurements to verify whether it is still within safe

bounds, and possibly to correct it.

The envisaged intelligent support system will

give advice to a patient on when to take which

amount of insulin or a meal. This advice is based on

a prediction of the blood glucose level using the

most recent measurement and the activities listed in

the electronic agenda. The listed activities influence

the blood glucose level, but also determine the time

points when insulin or a meal can be taken. For

example, in the middle of a sporting activity of

while working, it is not easily possible to take a meal

or insulin. The system could be implemented as an

advanced mobile phone or PDA application. Blood

glucose measurements will ideally be transferred

form the electronic device (see Figure 1) via a

wireless technology such as Bluetooth, but could

also be manually typed in into the application.

Figure 1: Electronic blood glucose meter.

For the prediction of the glucose level, the model as

explained in the previous section is used. The

parameters in the model should be fitted to the

personal characteristics of the patient. For this

fitting, there are quite a number of approaches (De

Geatano and Arino, 2000). In this paper, we assume

that the parameter fitting has been implemented

using one of the described techniques. Our

intelligent support system will use the model with

the fitted parameters and dynamically determine the

amount of insulin to be taken.

The system internally uses a list of activities and

associated values for the q parameters. Each type of

activity can have different parameters. For example,

walking could have different parameters for the

utilization of glucose and insulin than intense

sporting. The activities are read from the agenda,

and from the latest time point of measurement, the

current glucose level is calculated based on the

activities that are undertaken since the last

measurement. In addition, the upcoming activities

are used to predict the blood glucose level at the end

of the next activity that still has to be started. For

example, when a person is currently working and the

next activity will be cycling, the glucose level at the

end of the cycling activity is measured. In case this

measurement is too high, advice is given to take

insulin at the end of the current activity. In case this

measurement is too low, advice is given to take

some food at the end of the current activity. The

amount of insulin or food is dynamically determined

by simulation within the support system. At the end

of the current activity, the patient will get a message,

for example via his mobile phone application, to

take a specific amount of insulin or food before the

next activity.

4 SIMULATION EXPERIMENTS

The model and prediction rules that are used by the

system have been implemented in Matlab. A number

of simulation experiments have been run in this

environment. In these experiments, the activities of a

person during two consecutive days are simulated.

Table 1 gives an overview of the activities and the

time points. Note that the simulation time uses units

of 15 minutes.

For the parameters, values were used that are

found in the literature as realistic values for a

specific person. Specifically, we used the parameters

of subject 2 in (Gaetano and Arino, 2000): p

= 100,

= 0.1, p

= 0.2196, p

= 0.0064, p

= 0, p

= 23, p

= 0.096, p

= 0.5, I

= 0, G

= 120. Note that p

and

are 0 because we consider a diabetic patient. For

the desired minimum and maximum glucose levels,

we use 80 and 120 mg/dL (Erzen et al, 2000).

HEALTHINF 2010 - International Conference on Health Informatics

100

Figure 2: Blood glucose level of a diabetic patient without insulin intake.

Table 1: List of activities during two days.

Activity Clock

time

Time points in

simulation

Sleeping till 7am 0:00 0 96

Breakfast 7:00 28 124

Cycling / driving 7:30 30 126

Office work 8:15 33 129

Coffee 10:15 41 137

Office work 10:30 42 138

Lunch 12:30 50 146

Office work 13:00 52 148

Tea 16:00 64 160

Office work 16:15 65 161

Cycling / driving 17:00 68 164

Diner 17:45 71 167

Relaxing 18:30 74 170

Intense sporting / no sporting 19:30 78 174

Relaxing 20:30 82 178

Sleeping till 0:00 22:30 90 186

Sleeping till 7am 0:00 96 192

4.1 Blood Glucose Level without

Insulin Intake

The first simulation shows the blood glucose level

for a person that does not produce any insulin

anymore. At the start of the simulation, there is still

a small amount of insulin available (0.5 μU/ml),

however, this dissolve in a few hours. It can be seen

that the blood glucose level will be almost always

too high (see Figure 2).

4.2 Regular Insulin Intake with and

without Physical Activities

In the second set of simulations the glucose level of

a patient that is treated with a schema of regular

insulin intake doses. We assume in the simulation

that insulin is taken just before every meal,

effectively three times per day. The second

assumption is that a patient takes a lower dose of

insulin if physical activities are undertaken during

the day. We did this simulation for two different

scenarios: one with physical activities, in which the

person uses a bicycle to commute and does sporting

in the evening, and one in which the person drives to

his work by car and does no sporting. For the effect

of physical activities on the blood glucose balance,

we used a q

value of 0.25 for cycling and 0.5 for

intense sporting. The effect of the duration of the q

effect was set to 24 hours. The parameters q

and q

were both set to 0.25; no empirical values were

available. The effect on the blood glucose level and

the insulin is depicted in Figure 3 and 4.

It can be seen in Figure 4 that the patient takes a

smaller amount of insulin on a regular basis using

his common sense to keep the blood glucose within

safe boundaries in the scenario in which physical

activities are undertaken.

4.3 Prediction of Maximum and

Minimum Glucose Levels

To give a person intelligent support about his insulin

intake, we have to predict the effect of the activities

on the future blood glucose level. We do this by

running a simulation of the future values of the

blood glucose level during the current and next

activity at every time point within the simulation of

the scenarios. For this, we determine the end of the

next activity, take the planned activities into account,

AN INTELLIGENT SUPPORT SYSTEM FOR DIABETIC PATIENTS

101

Figure 3: Simulation of a diabetic patient that takes regular insulin dose with physical activities.

Figure 4: Simulation of a diabetic patient that takes regular insulin dose without physical activities

Figure 5: The predicted maximum and minimum blood glucose level during the current and next activity.

and simulate the blood glucose level till the end of

the next activity, assuming that no insulin will be

taken. Then, the maximum and minimum levels of

the blood glucose during that period are determined.

Figure 5 illustrates how this would look for the

scenario in which no insulin is taken (i.e. the

scenario depicted in Figure 2; the jigsaw pattern is a

side effect of using a small time step in the

simulation.)

When it is predicted that the maximum glucose

level will become too high (in this case > 120) till

the end of the next activity, the system will run

another simulation to predict the effect of taking a

standard insulin dose at the end of the current

activity. When it is predicted that the minimum

glucose level will become too low (in this case <

80) before the end of the next activity, the system

will run another simulation to predict the effect of

taking a standard meal(e.g. a cup of coffee, a

chocolate bar) at the end of the current activity.

Based on the size of the effect, the optimal dose is

determined. This is done by comparing the required

effect and the achieved effect with the standard dose.

HEALTHINF 2010 - International Conference on Health Informatics

102

Figure 6: Simulation of a patient using the intelligent support system without physical activities.

For example, if a standard dose of insulin reduces

the excess of the predicted level over the maximum

level by 30%, the advised dose is 100/30 = 3.33

times the standard dose.

4.4 Using the Intelligent Support

System for Insulin and Food Intake

We also ran a number of simulations of scenarios in

which patients actually follow the advice of the

intelligent support system. In these scenarios, the

advised dose of insulin is actually taken, and the

effect of this insulin is taken into account in the next

predictions. We show two scenarios: the first one is

the one without physical activities (Figure 6), the

second one with physical activities (Figure 7).

The figures show that the system is able to adapt

automatically to the activities of the person as

registered in his electronic agenda. In the scenario

without physical activities (Figure 6) the person gets

advice to take insulin three times per day with a dose

that corresponds to an insulin level increase of

around 3 μU/ml in the blood. No advice about

additional meals is given: it can be seen in Figure 6

that the glucose intake is standard and corresponds

to 5 time regular meals during the day, such as

breakfast, coffee , lunch, tea and dinner.

In the second scenario (see Figure 7), the advice

is to take insulin three times per day and five

additional meals during the first day and three

times per day insulin and one time an additional meal

during the second day. During the first day of the

second scenario the glucose intake occurs ten

times a day instead of standard five and six times

during the second day.

In both scenarios, the blood glucose level is most

of the time below the advised maximum level and

above the advised minimum level. Moreover, the

advice is always given at appropriate times, i.e.

never in the middle of an activity or during the night.

5 DISCUSSION

In this paper, the working of an intelligent support

system for diabetic patients is presented. The system

is based on the existing technologies like mobile

phones with electronic agenda’s, electronic blood

glucose meters, and mathematical models of the

blood/insulin balance. Keeping the blood glucose

AN INTELLIGENT SUPPORT SYSTEM FOR DIABETIC PATIENTS

103

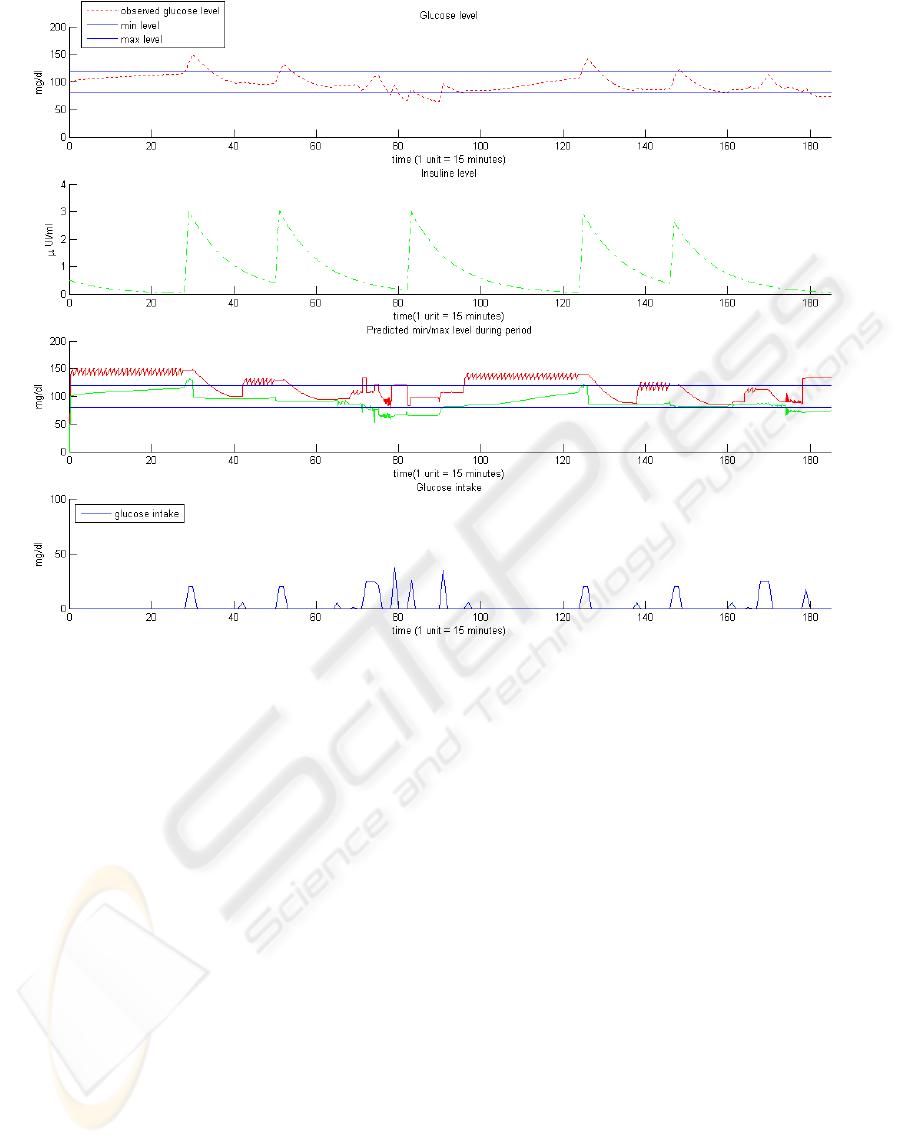
Figure 7: Simulation of a patient using the ambient support system with physical activities.

level within the safe boundaries by balancing insulin

dosages, glucose intake and physical activities is a

complicated task for diabetes patients. The

advantage of this system is that it adapts

automatically to the personal schedule of a patient

and gives concrete advice about insulin and food

intake at appropriate time points if it predicts that the

blood glucose level of the patient will rise above the

higher boundary or drop below the lower boundary at

the end of the next activity. The simulation results

demonstrated that in the scenario with the patient’s

physical activities the intelligent support system

helps better to maintain an appropriate blood glucose

level in comparison with the regular insulin

prescription.

Thus, the system could possible release a bit of

the burden of diabetic patients as it can predict the

effect of the upcoming activities more precisely than

humans. Moreover, the effective blood glucose level

management may minimize the progression of the

disease and reduce the risk of later complications

that accompany this chronic disease (Deutsch,

1994).

There are a number of extensions of this system

imaginable. First of all, one could think of using

continuous, non-invasive blood glucose measuring

techniques. At the moment, those are not yet

available, but it is expected that these become

available in the near future. Second, more specific

rules for restrictions on the advice can be

implemented, for example the minimum of

maximum dose, the minimal time between insulin

doses, the maximum doses per day, etc. These

extensions could make the system even more

realistic and more effective for patients.

REFERENCES

Ackerman, E., Gatewood, L. C., Rosevear, J. W. and

Molnar, G. D., 1965. Model studies of blood-glucose

regulation. Bulletin of Mathematical Biophysics 27:21-

37.

Bergman, R. N., Ider, Y. Z., Bowden, C. R. and Cobelli,

C., 1979. Quantitative estimation of insulin sensitivity.

American Journal of Physiology 236: E667-E677.

Bolie, V. W., 1961. Coefficients of normal blood glucose

regulation. Journal of Applied Physiology 16:783-788.

HEALTHINF 2010 - International Conference on Health Informatics

104

Derouich, M., Boutayeb, A., 2002. The effect of physical

exercise on the dynamics of glucose and insulin.

Journal of Biomechanics 35(7): 911-917.

Deutsch, T., Lehmann, E. D., Carson, E.R., Roudsari,

A.V., Hopkins, K.D., Sönksen, P.H., 1994. Time

series analysis and control of blood glucose levels in

diabetic patients.Computer Methods and Programs in

Biomedicine 41:167–182.

Erzen, F.C., Birol, G., Cinar, A., 2000. "Simulation

Studies on the Dynamics of Diabetes Mellitus," bibe,

pp.231, IEEE International Symposium on Bio-

Informatics and Biomedical Engineering (BIBE'00).

De Gaetano, A. and Arino, O., 2000.Mathematical

modelling of the intravenous glucose tolerance test,

Journal of Mathematical Biology 40: 136-168.

Goodyear, L.J., Kahn, B.B., 1998. Exercise, glucose

transport, and insulin sensitivity, Annual Review of

Medicine 49: 235-261.

Leaning, M.S. and Boroujerdi, M.A., 1991. A system for

compartmental modelling and simulation. Computer

Methods and Programs in Biomedicine 35:71–92.

Puckett, W.R., 1992. Dynamic modelling of diabetes

mellitus. PhD Thesis, University of Wisconsin -

Madison.

Sorensen, J.T., 1985. Physiologic model of glucose

metabolism in men and its use to design and asses

improved insulin therapies for diabetes. PhD Thesis,

MIT.

Tololo, G., Bergman, R. N., Finegood, D. T., Bowden, C.

R. and Cobelli, C., 1980. Quantitative estimation of

beta cell sensitivity to glucose in the intact organism: a

minimal model of insulin kinetics in the dog. Diabetes

29: 979-990.

Wild, S., Roglic, G., Green, A., Sicree, R., King, H., 2004.

Global prevalence of diabetes: estimates for the year

2000 and projections for 2030. Diabetes Care 27 (5):

1047–53.

Wikipedia, 2009. Diabetes management, section

Complexities relating to management,

http://en.wikipedia.org/wiki/Diabetes_management,

retrieved at June 8, 2009.

AN INTELLIGENT SUPPORT SYSTEM FOR DIABETIC PATIENTS

105