
MODELLING
MODIFIED ATMOSPHERE PACKAGING FOR
FRUITS AND VEGETABLES USING MEMBRANE SYSTEMS
Gabi Escuela
1
, Thomas Hinze
2
, Peter Dittrich
1
, Stefan Schuster
2
Friedrich Schiller University Jena,
1
Bio Systems Analysis Group and
2
Department of Bioinformatics, Jena, Germany
Mario Moreno-
´
Alvarez
U.N.E. Sim
´
on Rodr
´
ıguez, Laboratorio de Biomol
´
eculas, Canoabo, Venezuela
Keywords:
P systems, Modified Atmosphere Packaging, fruit modelling, membrane systems, respiration, temperature.
Abstract:
As living materials, post-harvested fruits and vegetables continue their metabolic activity, exhibiting progres-
sive biochemical changes. Optimisation of environmental conditions during storage of these fresh commodi-
ties is required in order to increase their shelf life. In this work we use P systems to abstract molecular inter-
actions that occur between plant organ, film and surrounding atmosphere factors involved in fresh fruit and
vegetable package designs. The proposed model constitutes a general framework to simulate the dynamical
behaviour of these systems, specially due to gas exchanges and temperature fluctuations. Moreover, the model
can be extended introducing other variables and processes that affect quality of such produces. This can be
considered, to the best of our knowledge, the first contribution of Membrane Computing in Food Engineering.
1 INTRODUCTION
Membrane systems (P
˘
aun and Rozenberg, 2002), also
called P systems, had emerged to assist in the mod-
elling of systems of concurrent reactions taking place
in compartments, so as occur in biological systems. In
this paper we use P systems as membrane structures
delimiting compartments that contain multisets of ob-
jects representing molecules. Compartments configu-
ration changes over time (evolve) according to given
rules that represent biochemical reactions and diffu-
sions. In contrast to ODE-based approaches, each
single molecule within the entire system is repre-
sented explicitly as individual entity. Capturing as-
pects of structural dynamics (changes in the mem-
brane structure as well as in the composition of com-
plex molecules) is seen as an advantageous feature of
P systems. Inclusion of reaction kinetics into this for-
malism can be done by discretised kinetic laws (Hinze
et al., 2006). We applied this mathematical formalism
to a real known problem in fruits and vegetables post-
harvest processing.
Fresh fruits and vegetables are living materials
that continue to respire after harvesting exhibiting
progressive biochemical changes. Food Engineer-
ing methods to preserve freshness of post-harvest
produces include low temperature storage and spe-
cial packaging technologies, mainly Modified Atmo-
sphere Packaging (MAP). MAP of fresh fruits and
vegetables refers to the technique of enveloping the
produce in a sealed container of polymeric film in or-
der to modify the O
2
and CO
2
concentrations inside
the package, reducing metabolic activity and increas-
ing shelf life (Paul and Clarke, 2002).
Designing MAP systems is a complex task that
involves considerations about many interrelated envi-
ronmental (as temperature and atmosphere composi-
tion), biological and package technology factors. Ba-
sic biological processes are respiration, transpiration,
ethylene production and compositional changes due
to metabolism. The variability of responses to internal
and external signals depends on the characteristic of
each plant organ type, developmental stage and physi-
ological condition. In addition, much of the behaviour
of a MAP system at cellular level are not fully under-
stood. As examples we can refer to the little knowl-
edge about the effect of CO
2
on the activity of respira-
tory enzymes (Ho et al., 2008). Moreover, the contri-
bution of the biochemical changes that alters physical
properties of cell walls and tissues modifying the tex-
ture of the produce is not known in detail (Gross et al.,
2004). On the other hand, the mechanism of ethylene
306
Escuela G., Hinze T., Dittrich P., Schuster S. and Moreno-Álvarez M. (2010).
MODELLING MODIFIED ATMOSPHERE PACKAGING FOR FRUITS AND VEGETABLES USING MEMBRANE SYSTEMS.
In Proceedings of the Third International Conference on Bio-inspired Systems and Signal Processing, pages 306-311
DOI: 10.5220/0002749103060311
Copyright
c
SciTePress
signal transduction that coordinates fruit ripening pro-
cesses, is another aspect subject to study (Alexander
and Grierson, 2002).
The difficulty to test different combination of
gases and temperatures and the complexity of exper-
imental setup for MAP systems had lead to the de-
velopment of various mathematical models (Exama
et al., 1993; Tijskens et al., 2001; Paul and Clarke,
2002; Ho et al., 2008) and software (Mahajan et al.,
2007). In the literature, many respiration models are
empirical fits of experimental data, based on one par-
ticular type and variety of fruit or vegetable, and most
of them are based on the principles of enzyme ki-
netics and are represented using ODEs (for reviews
see (Fonseca et al., 2002; Rodriguez-Aguilera and
Oliveira, 2009)). However, there exists some lack on
studies about the dynamical behaviour of these sys-
tems in terms of changes in environmental conditions,
so as produce composition and physiology due to de-
velopmental processes (Fonseca et al., 2002). It is
worth mentioning that post-harvested fruits and veg-
etables, unlike other living materials, can be consid-
ered as less robust systems, as their responses on en-
vironmental fluctuations depends mostly on their ac-
tual configuration of biochemical components. In this
context, some authors (G
´
enard et al., 2007; Maha-
jan et al., 2007) have considered the potential ben-
efits of a systematic analysis or process-based mod-
elling approach for fruits and vegetables. Consider-
ing that understanding the reaction network underly-
ing MAP systems can give food experts more knowl-
edge about emergent properties of packaged fruits and
vegetables, we propose a framework based on mem-
brane systems that abstracts basic biochemical reac-
tions that occur in MAP systems. In the future, the
proposed model can serve as a predictive tool to sim-
ulate changes in fresh produce on the molecular level,
due to changes in environmental conditions.
This paper is organized as follows: in Section 2
we present a P system framework for MAP, including
the description of components, reaction kinetics and
evolution of the system. Section 3 shows an applica-
tion of the framework considering a package under
modified atmosphere containing two produces. Fi-
nally, in Section 4 we point out some benefits of using
our framework and future extensions of it.
2 A P SYSTEM-BASED MAP
We abstract a fruit or vegetable as a graph of cells
or modules, like tissue P systems (Mart
´
ın-Vide et al.,
2003). Each cell represents a compartment that con-
tains species, and at a specific time, the contents of the
compartment determine the cell configuration. This
serves as a mechanism to differentiate one cell from
other, given the possibility to creating diverse tissue
types, as occurs for example in fruits epicarp, meso-
carp and endocarp tissues (G
´
enard et al., 2007). Addi-
tionally, as gas consumption-production occur inside
the cells, at the mitochondria level, and is stated that
gas diffusion between cells depends on the geometry
of the produce (Ho et al., 2008), differences in gas
content in cells that conform a determinate region can
adequately be represented. This is also in accordance
to the idea that the ripening process usually starts
in one region of a fruit and spreads to neighbour-
ing regions, due to ethylene diffusion starting from
promoter cells (Alexander and Grierson, 2002). Pro-
duces into the package are represented as a population
of membranes, giving the advantage that the model
can deal with distinct fruits and vegetables within the
same film, or the same produce in distinct develop-
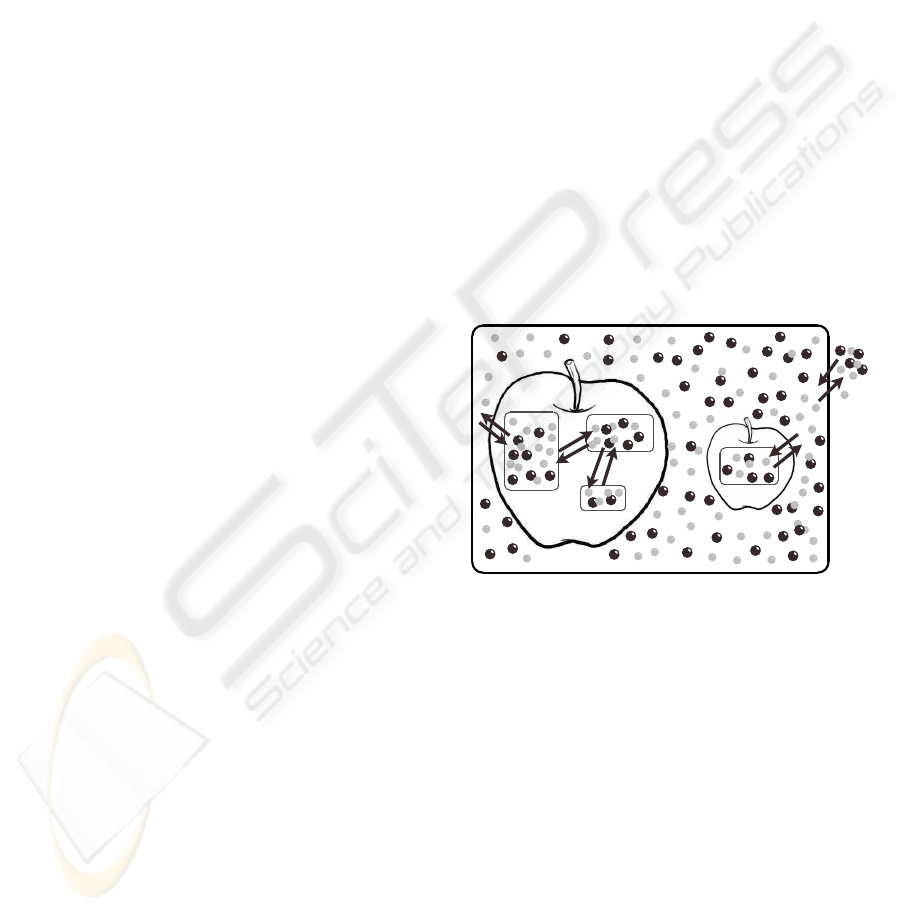
mental stages, varieties and/or presentations. Figure
1 shows as example, the schematic representation for
such a system. In the next section we present the for-
mal specification of our model.
package
plant_1
plant_2
cell_1,1
cell_1,2
cell_1,3
cell_2,1
Figure 1: A schematic representation for the MAP system
model. In this case, two produces share a package: plant
1
is
formed by three connected cells, and plant
2
is formed by a
single cell. Arrows represent paths for molecules (spheres)
diffusions.
Multiset Prerequisites. Let A be an arbitrary set and
N the set of natural numbers including zero. A multi-
set over A is a mapping F : A −→ N ∪{∞}. F(a), also
denoted as [a]
F
, specifies the multiplicity of a ∈ A in
F. Multisets can be written as an elementwise enu-
meration of the form {(a
1
,F(a
1
)),(a
2
,F(a
2
)),. ..}
since ∀(a,b
1
),(a, b
2
) ∈ F : b
1
= b
2
. The
support supp(F) ⊆ A of F is defined by
supp(F) = {a ∈ A | F(a) > 0}. A multiset F
over A is said to be empty iff ∀a ∈ A : F(a) = 0. The
cardinality |F| of F over A is |F| =
∑
a∈A
F(a). Let
F
1
and F
2
be multisets over A. F
1
is a subset of F
2
,
denoted as F
1
⊆ F
2
, iff ∀a ∈ A : (F
1
(a) ≤ F
2
(a)).
MODELLING MODIFIED ATMOSPHERE PACKAGING FOR FRUITS AND VEGETABLES USING MEMBRANE
SYSTEMS
307

Multisets F
1
and F
2
are equal iff F
1
⊆ F
2
∧ F
2
⊆ F
1
.
The intersection F
1
∩ F
2
= {(a,F(a)) | a ∈
A ∧ F(a) = min(F
1
(a),F
2
(a))}, the multiset sum
F
1
] F
2
= {(a,F(a)) | a ∈ A ∧ F(a) = F
1
(a) + F
2
(a)},
and the multiset difference F
1
ª F
2
= {(a,F(a)) | a ∈
A ∧ F(a) = max(F
1
(a) − F
2
(a),0)} form mul-
tiset operations. Multiplication of a multiset
F = {(a, F(a)) | a ∈ A} with a scalar c, denoted c · F,
is defined by {(a,c · F(a)) | a ∈ A}.
P System Components. Let N
+
= N \ {0} be the set
of natural numbers without zero, and m,n ∈ N
+
. We
define a P system for a MAP system as a construct:
Π
MAP
= (µ,S, plant
1
,. .., plant
m
,G, L
0
,
D
1
,. .., D
d
, f
1
,. .., f
d
,∆τ)
where:
• µ = [[[]
cell
1,1
...[]
cell
1,n
1
]
plant
1
...[[]
cell
m,1
...[]
cell
m,n
m
]
plant
m
]
package
is
the spatial system structure composed of three inner levels: package,
plants, and cells,
• S is a set of chemical species,
• plant
1
,.. . , plant
m
represent the produces into the package,
• G is a set of global parameters,
• L
0
: S → N is a multiset of axioms representing the initial molecular
configuration,
• D
ν
is a diffusion (communication) rule among package and external
environment (ν = 1,.. . ,d),
• f
ν
: (S → N) → N is a kinetic function attached to diffusion rule D
ν
,
• ∆τ ∈ R
+
is the time discretisation interval.
A diffusion rule D
ν
can be of the form [s] → []s for
molecules s ∈ S leaving the package and released to
the external environment, and []s → [s] for molecules
entering the package, respectively.
Furthermore, each plant
i
is defined as a tuple:
plant
i
= (N
i
,E
i
,G
i
,D
i,1
,. .., D
i,d
i
, f
i,1
,. .., f
i,d
i
)
where:
• N
i
= {cell
i,1
,.. . ,cell
i,n
i
} defines a set of cells within plant i,
• E
i
⊆ N
i
× N
i
specifies a set of directed edges (diffusion channels be-
tween cells),
• G
i
is a set of plant (organ) specific parameters,
• D
i,κ
represents a diffusion rule inside plant i and between plant i and
package (κ = 1,... , d
i
),
• f
i,κ
is a kinetic function attached to diffusion rule D
i,κ
.
Here, a diffusion rule can be of the form
[s]
cell
p,q
→ []
cell
p,q
s for molecules s ∈ S leaving cell
p,q
and spread out into the package. A rule of the
form []
cell
p,q
s → [s]
cell
p,q
describes molecules entering
cell
p,q
from the package. Finally, a rule of the form
[s]
cell
p,q
→ [s]
cell
x,y
formulates the directed transport of
molecule s along the edge (cell
p,q
,cell
x,y
) ∈ E
i
.
Each cell
i, j
is defined as a tuple
cell
i, j
= (L
i, j,0
,R
i, j,1
,. .., R
i, j,r
i, j
, f
i, j,1
,. .., f
i, j,r
i, j
)
where:
• L
i, j,0
: S → N is a multiset of axioms representing its initial molecular
configuration,
• R
i, j,k
= (A
i, j,k
,B
i, j,k
) with A
i, j,k
: S → N (multiset of reactants) and
B
i, j,k
: S → N (multiset of products) specifies a reaction rule including
its stoichiometric factors,
• f
i, j,k
: (S → N) → N is a function corresponding to kinetics of reaction
R
i, j,k
.
System Evolution. A P system of the form Π
MAP
evolves by successive progression of its configuration
at discrete points in time t ∈ N for what we assume a
global clock. Two consecutive dates t and t + 1 spec-
ify a time span ∆τ. A system step at time t consists
of three modification stages carried out from outer
to inner spatial components of the system. Firstly,
the diffusion between package and its environment is
considered. To this end, the rules D
1
up to D
d
are
employed. Afterwards, the diffusion between pack-
age and cells as well as the intracellular diffusion is
utilised by employing the rules D
i,κ
for each plant
i = 1,.. .,m. The last modification stage concerns ap-
plication of the reaction rules specified in each cell.
To cope with conflicts that can occur if the available
amount of substrate cannot satisfy all matching dif-
fusion and reaction rules, we prioritise all rules by
their index: D
1
> D
2
> ... > D
d
. Moreover, for each
plant i: D
i,1
> D
i,2
> ... > D
i,d
i
and for each cell i, j:
R
i, j,1
> R
i, j,2
> .. . > R
i, j,r
i, j
. Thus, we keep determin-
ism of the system evolution and enable mass conser-
vation. An alternative method for coping with con-
flicts is randomisation in selection and sequentialisa-
tion of diffusion and reaction rules.
The application of an arbitrary rule is organised
into two consecutive steps. The first step identifies
all molecules from the rule’s left hand side acting as
sources for diffusion or reactants. These molecules
are removed from the current configurations. Corre-
sponding molecules from the right hand side (desti-
nations in case of diffusion and products in case of
reactions) are then added. We formulate discretised
reaction-diffusion kinetics by specification of scalar
functions f : M → N based on a multiset M : S → N.
Each function f converts the current configuration (L
t
or L
i, j,t
), a multiset of objects, into the number of
turns for application of the corresponding diffusion or
reaction rule. Here, kinetic laws
ˆ
f(s) for each species
s ∈ S employ the multiplicity of its occurrences to for-
mulate the corresponding reaction rate. For updating
the entire system configuration, we define an iteration
scheme as shown in Figure 2.
BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing
308

Stage 1 (diffusion between package and external environment):
∀α = 1,..., d
diffusion rule conditions action
D
α
= [σ] → []σ (σ ∈ S) ∧ ({(σ, f
α
)} ⊆ L
t
) L
t
:= L
t
ª {(σ, f
α
)}
D
α
= []σ → [σ] (σ ∈ S) L
t
:= L
t
] {(σ, f
α
)}
with f
α
(L
t
) =
¥
k
α
(G) · ∆τ ·
ˆ
f(|L
t
∩ {(σ,∞)}|)
¦
Stage 2 (diffusion between plant cells and package):
∀i = 1, ... ,m
∀α = 1,. .., d
i
diffusion rule conditions action
D
i,α
= [σ]
cell
i, j
→ []
cell
i, j
σ (σ ∈ S) ∧ (cell
i, j
∈ N
i
) ∧ ({(σ, f
i,α
)} ⊆ L
i, j,t
)
L
i, j,t
:= L
i, j,t
ª {(σ, f
i,α
)}
L
t
:= L
t
] {(σ, f
i,α
)}
D
i,α
= []
cell
i, j
σ → [σ]
cell
i, j
(σ ∈ S)∧ (cell
i, j
∈ N
i
) ∧ ({(σ, f
i,α
)} ⊆ L
t
)
L
t
:= L
t
ª {(σ, f
i,α
)}
L
i, j,t
:= L
i, j,t
] {(σ, f
i,α
)}
D
i,α
= [σ]
cell
i, j
→ [σ]
cell
i,k
(σ ∈ S)∧ (k 6= j) ∧ (cell
i, j
∈ N
i
) ∧ (cell
i,k
∈ N
i
)
∧((cell
i, j
,cell
i,k
) ∈ E
i
) ∧ ({(σ, f
i,α
)} ⊆ L
i, j,t
)
L
i, j,t
:= L
i, j,t
ª {(σ, f
i,α
)}
L
i,k,t
:= L
i,k,t
] {(σ, f
i,α
)}
with f
i,α
(L
t
) =
¥
k
i,α
(G,G
i
) · ∆τ ·
ˆ
f(|L
t
∩ {(σ,∞)}|)
¦
Stage 3 (reactions occurring within each cell):
∀i = 1, ... ,m
∀ j = 1, ... ,n
i
∀α = 1, ... ,r
i, j
reaction rule conditions action
R
i, j,α
= (A
i, j,α
,B
i, j,α
) f
i, j,α
· A
i, j,α
⊆ L
i, j,t
L
i, j,t
:= L
i, j,t
ª f
i, j,α
· A
i, j,α
] f
i, j,α
· B
i, j,α
with f
i, j,α
(L
i, j,t
) =
$
k
i, j,α
(G,G
i
) · ∆τ
∏
∀c∈supp(A
i, j,α
):(R
i, j,α
=(A
i, j,α
,B
i, j,α
))
ˆ
f(|L
i, j,t
∩ {(c,∞)}|)
|A
i, j,α
∩{(c,∞)}|
%
Increment time t:
L
t+1
:= L
t
∀i = 1, ... ,m
∀ j = 1, ... ,n
i
L
i, j,t+1
:= L
i, j,t
Figure 2: Iteration scheme for the temporal evolution of Π
MAP
system.
3 SIMULATION
As a first application, we introduced as rules into the
model only the basic processes involved in a MAP
design: respiration and fermentation, so as gas dif-
fusion between membranes. Respiration rate can be
expressed in terms of O
2
consumed or CO
2
produced.
The respiratory quotient (RQ), the ratio of CO
2
pro-
duced to O
2
consumed, ranges from about 0.7 to 1.4
depending on the substrate and its metabolic state (if
the substrate is a lipid, RQ < 1, and RQ > 1 for or-
ganic acids)(Fonseca et al., 2002). When carbohy-
drates are aerobically respired, the RQ is near 1, and
the reaction is represented by Eq. (1). The influence
of gas composition on respiration rates of produce has
been widely represented by Michaelis Menten-type
equation (Fonseca et al., 2002). In this context, respi-
ration rate is considered as a function of concentration
in terms of enzymatic reaction, with O
2
in the place
of substrate and the product CO
2
acting as inhibitor.
C
6
H
12
O
6
+ 6 O
2
→ 6CO
2
+ 6 H
2
O + energy (1)
Transpiration occurs due to the fact that fruits and
vegetables internal atmosphere is saturated with wa-
ter vapour, while external atmosphere contains lesser.
Therefore, water loss rate depends on the external and
internal water vapour pressure gradient.
Temperature dependence over respiratory rate and
over film permeability was represented using Arrhe-
nius equation (Eq. 2).
k = F × e
−E
a
/R×T
(2)
MODELLING MODIFIED ATMOSPHERE PACKAGING FOR FRUITS AND VEGETABLES USING MEMBRANE
SYSTEMS
309

where E
a
is the activation energy, expressed in joule
per mol, defined as the energy that must be overcome
for a chemical reaction to occur; R is the gas constant
(≈ 8.314 J · K
−1
mol
−1
), T the absolute temperature,
F is the pre-exponential factor that represents the total
number of molecular collisions per second; and k cor-
responds to the number of collisions per second that
result in a reaction. This can be related to the proba-
bilistic approach to P systems introduced by (Arde-
lean and Cavaliere, 2003) in order to obtain more
biological-like models. In this context, the Arrhenius
exponential term can be viewed as the probability per
time unit that the reaction takes place.
In order to apply our model, we simulate the dy-
namical behaviour of an instance of a Π
MAP
with two
hypothetical fruits as it is shown in Fig. 1, using
continuous film and passive MAP as package tech-
niques. Rules that use symbol between reactants
and products must been interpreted as reversible reac-
tions. Into the formalism described in Fig. 2, a rule of
the form D
α
= [σ] []σ, for example, consists in the
following two rules, in order of application: [σ] → []σ
and []σ → [σ].
S = {CO2,Ethanol,Glucose,H2O,O2}
G = {M, T, R,A,E,CO2ex,H2Oex,O2ex,EaCO2, E aO2, pCO2, pO2, pH2O}
N
1
= {cell
1,1
,cell
1,2
,cell
1,3
}
N
2
= {cell
2,1
}
G
i
: {ErO2, rO2,ErCO2 f ,rCO2 f } ∀i ∈ {1,2}
D
1
: []
package
O2 [O2]
package
f
1
(L
t
) =
$
A
E
· (O2ex − L
t
(O2)) · pO2 · e
−EaO2
R · T
%
D
2
: [CO2]
package
[]
package
CO2
f
2
(L
t
) =
$
A
E
· (L
t
(CO2) − CO2ex) · pCO2 · e
−EaCO2
R · T
%
D
3
: [H2O]
package
[]
package
H2O
f
3
(L
t
) =
¹
A
E
· (L
t
(H2O) − H2Oex) · pH 2O
º
D
1,1
: []
cell
1,1
O2 [O2]
cell
1,1
f
1,1
(L
t
) = k
1,1
· L
t
(O2)
D
1,2
: [CO2]
cell
1,1
[]
cell
1,1
CO2 f
1,2
(L
t
) = k
1,2
· L
t
(CO2)
D
1,3
: [H2O]
cell
1,1
[]
cell
1,1
H2O f
1,3
(L
t
) = k
1,3
· L
t
(H2O)
D
1,4
: [O2]
cell
1,1
[O2]
cell
1,2
f
1,4
(L
t
) = k
1,4
· L
t
(O2)
D
1,5
: [CO2]
cell
1,2
[CO2]
cell
1,1
f
1,5
(L
t
) = k
1,5
· L
t
(CO2)
D
1,6
: [H2O]
cell
1,2
[H 2O]
cell
1,1
f
1,6
(L
t
) = k
1,6
· L
t
(H2O)
D
1,7
: [O2]
cell
1,2
[O2]
cell
1,3
f
1,7
(L
t
) = k
1,7
· L
t
(O2)
D
1,8
: [CO2]
cell
1,3
[CO2]
cell
1,2
f
1,8
(L
t
) = k
1,8
· L
t
(CO2)
D
1,9
: [H2O]
cell
1,3
[H 2O]
cell
1,2
f
1,9
(L
t
) = k
1,9
· L
t
(H2O)
D
2,1
: []
cell
2,1
O2 [O2]
cell
2,1
f
2,1
(L
t
) = k
2,1
· L
t
(O2)
D
2,2
: [CO2]
cell
2,1
[]
cell
2,1
CO2 f
2,2
(L
t
) = k
2,2
· L
t
(CO2)
D
2,3
: [H2O]
cell
2,1
[]
cell
2,1
H2O f
2,3
(L
t
) = k
2,3
· L
t
(H2O)
R
i, j,1
: Glucose+ 6 O2 → 6 CO2 + 6 H2O ∀i ∈ {1, 2}∧ j ∈ {1,2,3}
f
i, j,1
(L
i, j,t
) =
L
i, j,t
(Glucose)
Θ
i, j,1,1
+ L
i, j,t
(Glucose)
·
L
i, j,t
(O2)
6
Θ
i, j,1,2
+ L
i, j,t
(O2)
6
·
M
i
3
· rO2 · e
−ErO2
R · T
R
i, j,2
: Glucose → 2 Ethanol + 2 CO2 ∀i ∈ {1, 2}∧ j ∈ {1,2,3}
f
i, j,2
(L
i, j,t
) =
$
L
i, j,t
(Glucose)
Θ
i, j,2,1
+ L
i, j,t
(Glucose)
· M
i
· rCO2 f · e
−ErCO2 f
R · T
%
Temperature is represented by T and expressed
in Kelvin (K). O
2
, CO
2
and H
2
O abundances in the
outside are represented by O2ex, CO2ex and H2Oex
respectively. A and E symbolise the surface area in
cm
2
and the thickness of the packaging film in mil
(1mil = 0.00254cm). pO2 and pCO2 represent the
reference film permeability in mL · mil · cm
2
· hr
−1
·
atm
−1
for O
2
, CO
2
and H
2
O, respectively. EaO2 and
EaCO2 symbolise the permeability activation energy
expressed in J · mol
−1
for O
2
and CO
2
, respectively.
M
i
symbolises mass of the produce i in kg. For sim-
plicity, we assume that each cell in a produce has the
same mass. rO2 and rCO2 f corresponds to the preex-
ponential factor for produce respiration and fermen-
tation in mL · kg
−1
· hr
−1
. ErO2 and ErCO2 f rep-
resent the respiration and fermentation activation en-
ergy for the produce expressed in J · mol
−1
. Most of
the values for these symbols were taken from the liter-
ature (Exama et al., 1993). Symbols O2, CO2, H2O,
Ethanol and Glucose represent amounts of species
O
2
, CO
2
, H
2
O, Ethanol and Glucose. Initial values
for these symbols in each compartment and the rest
of the parameters were assigned empirically.
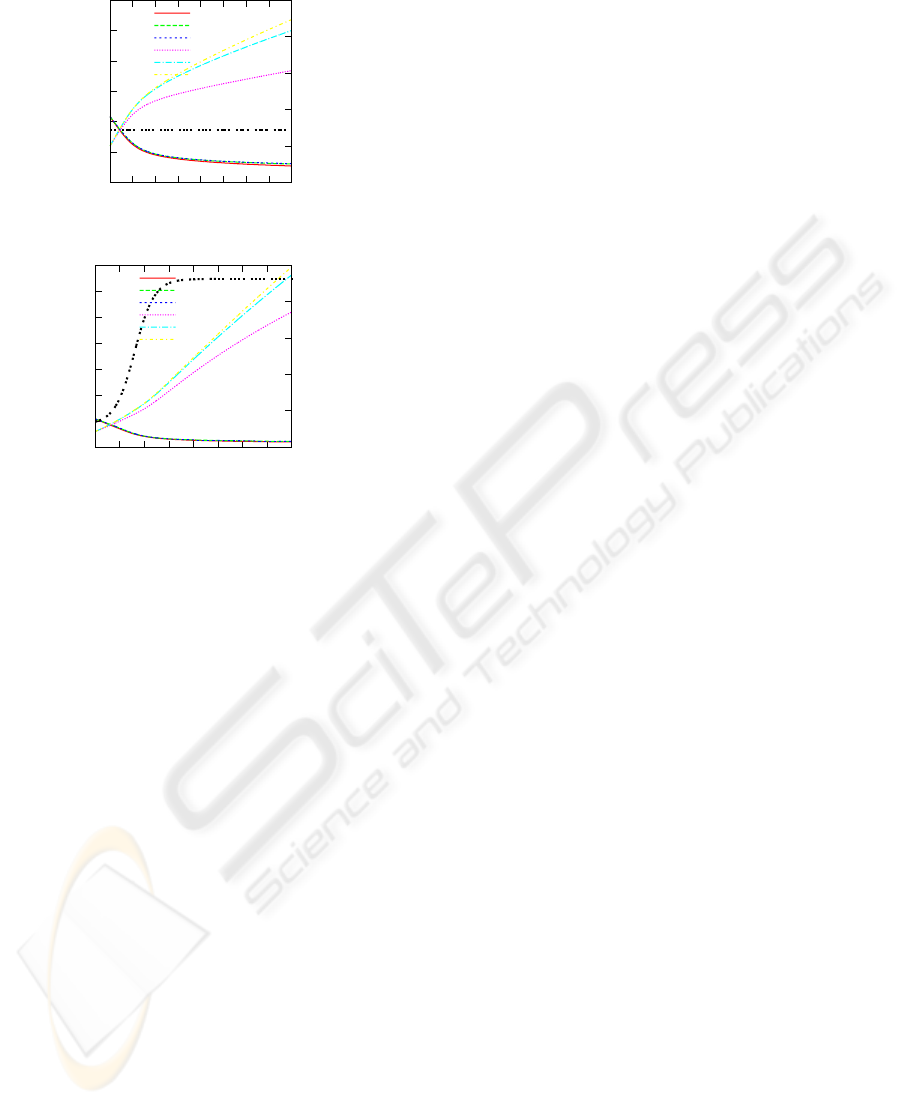
Figure 3 shows the corresponding courses of
plant
1
internal gas composition, resulting from fol-
lowing parameter setting for the discrete iteration
scheme: A = 100, E = 1, M
i
= 0.1, pO2
i
= 1620000,
EaO2
i
= 43100, pCO2
i
= 238000, EaCO2
i
= 34300,
rO2
i
= rCO2 f
i
= 3 × 10
14
, ErO2
i
= ErCO2 f =
70700, pH2O
i
= 1, Θ
i, j,1,k
= 1, for i ∈ {1, 2} and j ∈
{1,2, 3} and k ∈ {1,2}; k
1, j
= 0.2 for j ∈ {1,..., 9},
k
2, j
= 0.2 for j ∈ {1,... ,3}. A fixed value T =
277.15 was considered for a constant temperature sce-
nario, and transient values for 273.15 ≤ T ≤ 293.15
were obtained through a sigmoid function to repre-
sent changes in temperature over time in another sce-
nario. Simulations have been performed using Co-
pasi (Hoops et al., 2006). Differences in internal
gas composition of plant
1
have been observed dur-
ing time due to the interplay between cellular respira-
tion and fermentation processes and intercellular dif-
fusion. Those differences could determine the form
of maturation of the produce, in this case, from the
center to the skin. An equilibrium is reached in the
package gas composition, while respiration rates of
the produces diminished.
4 CONCLUSIONS
Using a membrane based model for MAP, we pre-
sented a framework that is able to abstract packag-
ing for different fruit and vegetable types, varieties
or developmental stages. Respiration of the produce
BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing
310
0
5e+023
1e+024
1.5e+024
2e+024
2.5e+024
3e+024
0 0.5 1 1.5 2 2.5 3 3.5 4
270
275
280
285
290
295
Particle numbers
Temperature (K)
Time
Plant
1
O2
11
O2
12
O2
13
CO2
11
CO2
12
CO2
13
0
1e+024
2e+024
3e+024
4e+024
5e+024
6e+024
7e+024
0 0.5 1 1.5 2 2.5 3 3.5 4
270
275
280
285
290
295
Particle numbers
Temperature (K)
Time
Plant
1
O2
11
O2
12
O2
13
CO2
11
CO2
12
CO2
13
Figure 3: Dynamical behaviour for gas composition for
plant
1
in constant and varying temperature scenarios.
is considered as the basic process when modelling
MAP, and predictions about the dynamical behaviour
of such systems can be improved taking into ac-
count environmental, biological and technical factors.
Our approach allows extensions including other low
level processes, such as ethylene signaling pathway,
cell/tissue rupture due to produce cutting and trans-
port of other molecules, that can been easily modeled
using P systems. When the formalism showed in Fig-
ure 2 is hidden in a software, the specification is in-
tuitive an accessible for an expert focussing on MAP
modelling. Finally, the quality of the packaged pro-
duce (taste, texture, colour and appearance) is based
on some subjective consumer evaluation. These traits
are based on specific product properties, such as sugar
content, volatile production and cell wall structure
(Tijskens et al., 2001), and therefore can be intro-
duced into the model through reactions, as a mech-
anism to obtain more knowledge about the impact of
packaging conditions over product quality.
ACKNOWLEDGEMENTS
GE is supported by Universidad Sim
´
on Bol
´
ıvar (Cara-
cas, Venezuela) and Deutscher Akademischer Aus-
tausch Dienst (DAAD) Grant A/08/94489.
REFERENCES
Alexander, L. and Grierson, D. (2002). Ethylene biosynthe-
sis and action in tomato: a model for climacteric fruit
ripening. J. Exp. Bot., 53(377):2039–2055.
Ardelean, I. and Cavaliere, M. (2003). Modelling biological
processes by using a probabilistic P system software.
Natural Computing, 2(2):173–197.
Exama, A., Arul, J., Lencki, R., Lee, L., and Toupin, C.
(1993). Suitability of plastic films for modified atmo-
sphere packaging of fruits and vegetables. J Food Sci,
58(6):1365–1370.
Fonseca, S., Oliveira, F., and Brecht, J. (2002). Modelling
respiration rate of fresh fruits and vegetables for mod-
ified atmosphere packages: a review. J Food Eng,
52(2):99–119.
G
´
enard, M., Bertin, N., Borel, C., Bussieres, P., Gautier, H.,
Habib, R., Lechaudel, M., Lecomte, A., Lescourret,
F., Lobit, P., and Quilot, B. (2007). Towards a vir-
tual fruit focusing on quality: modelling features and
potential uses. J Exp Bot, 58(5):917–928.
Gross, K., Wang, C., and Saltveit, M. (2004). The com-
mercial storage of fruits, vegetables, and florist and
nursery stocks. Agriculture Handbook, 66.
Hinze, T., Lenser, T., and Dittrich, P. (2006). A protein sub-
structure based P system for description and analysis
of cell signalling networks. Lect Notes Comput Sci,
4361:409–423.
Ho, Q., Verboven, P., Verlinden, B., Lammertyn, J., Vande-
walle, S., and Nicolai, B. (2008). A continuum model
for metabolic gas exchange in pear fruit. PLoS Com-
putational Biology, 4(3):e1000023.
Hoops, S., Sahle, S., Gauges, R., Lee, C., Pahle, J., Simus,
N., Singhal, M., Xu, L., Mendes, P., and Kummer, U.
(2006). Copasi—a complex pathway simulator. Bioin-
formatics, 22(24):3067–3074.
Mahajan, P., Oliveira, F., J., M., and Frias, J. (2007). Devel-
opment of user-friendly software for design of modi-
fied atmosphere packaging for fresh and fresh-cut pro-
duce. Innovative Food Science and Emerging Tech-
nologies, 8(1):84–92.
Mart
´
ın-Vide, C., P
˘
aun, G., Pazos, J., and Rodr
´
ıguez-Pat
´
on,
A. (2003). Tissue P systems. Theor Comput Sci,
296(2):295–326.
Paul, D. and Clarke, R. (2002). Modelling of modified at-
mosphere packaging based on designs with a mem-
brane and perforations. J Membr Sci, 208(1–2):269–
283.
P
˘
aun, G. and Rozenberg, G. (2002). A guide to membrane
computing. Theor Comput Sci, 287(73–100):73–100.
Rodriguez-Aguilera, R. and Oliveira, J. (2009). Review of
design engineering methods and applications of active
and modified atmosphere packaging systems. Food
Engineering Reviews, 1(1):66–83.
Tijskens, L., Hertog, M., and Nicola
¨
ı, B. (2001). Food Pro-
cess Modelling. Woodhead Pub.
MODELLING MODIFIED ATMOSPHERE PACKAGING FOR FRUITS AND VEGETABLES USING MEMBRANE
SYSTEMS
311
