
P
ARALLEL CALCULATION OF
SUBGRAPH CENSUS IN BIOLOGICAL NETWORKS
Pedro Ribeiro, Fernando Silva and Lu
´
ıs Lopes
CRACS & INESC-Porto LA, Faculdade de Ci
ˆ
encias, Universidade do Porto
Rua do Campo Alegre 1021, 4169-007 Porto, Portugal
Keywords:
Biological networks, Complex networks, Graph mining, Network motifs, Parallel algorithms.
Abstract:
Mining meaningful data from complex biological networks is a critical task in many areas of research. One
important example is calculating the frequency of all subgraphs of a certain size, also known as the sub-
graph census problem. This can provide a very comprehensive structural characterization of a network and
is also used as an intermediate step in the computation of network motifs, an important basic building block
of networks, that try to bridge the gap between structure and function. The subgraph census problem is com-
putationally hard and here we present several parallel strategies to solve this problem. Our initial strategies
were refined towards achieving an efficient and scalable adaptive parallel algorithm. This algorithm achieves
almost linear speedups up to 128 cores when applied to a representative set of biological networks from dif-
ferent domains and makes the calculation of census for larger subgraph sizes feasible.
1 INTRODUCTION
A broad range of biological structures can be rep-
resented as complex networks. The study of such
networks is relatively recent and has received in-
creased attention by the scientific community (Alm
and Arkin, 2003). A large number of concepts and
techniques appeared to analyze and understand com-
plex networks from any domain, leading to an impres-
sive panoply of different measurements used to mine
interesting data from them (Costa et al., 2007).
One important measure is the frequency in which
subgraphs appear in a network. Sometimes we are
just interested in determining frequent patterns (Ku-
ramochi and Karypis, 2001), while in others we need
to determine a full count of all different classes of iso-
morphic subgraphs (Bordino et al., 2008). This last
option is also known as a subgraph census and can
provide a very accurate structural characterization of
a network. This is typically applied for subgraphs of a
specific size and it is normally limited to small sizes,
mostly for efficiency reasons. This has been done
not only on biological networks (Middendorf et al.,
2004), but also on other domains, such as social net-
works analysis, where the triad census is very com-
mon (Wasserman et al., 1994).
Subgraph census also plays a major role as an in-
termediate step in the calculation of other important
measures, such as network motifs (Milo et al., 2002),
which are basically subgraphs that are statistically
over-represented in the network (and conjectured to
have some functional significance). Network motifs
have applications on several biological domains, like
protein-protein interaction (Albert and Albert, 2004),
gene transcriptional regulation (Mazurie et al., 2005),
brain networks (Sporns and Kotter, 2004) and food
webs (Kondoh, 2008). Complex networks from other
domains can also be studied with motifs, like elec-
tronic circuits (Itzkovitz et al., 2005) or software ar-
chitecture (Valverde and Sol
´
e, 2005). The practi-
cal available algorithms and tools for network mo-
tifs all use a census to discover the frequency in the
original network and then calculate it again for a
series of similar randomized networks (Milo et al.,
2002; Wernicke, 2006). This is a computationally
hard problem that is closely related to the problem of
graph isomorphism (McKay, 1981). Some techniques
were developed to speedup the calculations, like sam-
pling (Kashtan et al., 2004), but they normally trade
accuracy for speed.
In all these applications, having a more efficient
way to calculate the census is highly desirable. As
we increase the size of the subgraphs, their frequency
increases exponentially and it becomes unfeasible to
count all of them using traditional approaches. More-
over, to date, almost all algorithms for complete sub-
56
Ribeiro P., Silva F. and Lopes L. (2010).
PARALLEL CALCULATION OF SUBGRAPH CENSUS IN BIOLOGICAL NETWORKS.
In Proceedings of the First International Conference on Bioinformatics, pages 56-65
DOI: 10.5220/0002749600560065
Copyright
c
SciTePress

graph census are sequential. Some exceptions exist,
particularly in the area of network motifs, but they
are scarce and still limited (c.f. section 2.3). One rea-
son is that present network motifs methods still resort
to the generation of hundreds of random networks to
measure significance. This puts the obvious opportu-
nity for parallelism not in the census itself but in the
generation of random networks and their respective
census. However, analytical methods to estimate the
significance are now appearing (Matias et al., 2006;
Picard et al., 2008) and once they are fully developed
the burden of the calculation will then reside on the
census of the original network.
Considering the relevance of calculating exhaus-
tive census and the computational complexity in-
volved, resorting to parallel algorithms to speedup
the calculation is, in our view, an approach that will
impact in many application areas, particularly in the
study of biological networks. The use of parallelism
can not only speed up the calculation of census, but
also allow the calculation of the census for subgraph
sizes that were until now unreachable.
This paper focuses on strategies for solving the
subgraph census problem in parallel. With this ob-
jective in mind we start with an efficient sequential
algorithm, ESU (Wernicke, 2006), and progressively
modify it to accommodate scalable parallel execution
and data-structures. This process led us to the for-
mulation of a novel adaptive parallel algorithm for
subgraph census that features a work sharing scheme
that dynamically adjusts to the available search-space.
The results obtained show that the algorithm is effi-
cient and scalable.
The remainder of this paper is organized as fol-
lows. Section 2 establishes a network terminology,
formalizes the problem we want to tackle and gives an
overview of related work. Section 3 details all the fol-
lowed parallel strategies and the algorithm we devel-
oped. Section 4 discusses the results obtained when
applied to a set of representative biological networks.
Section 5 concludes the paper, commenting on the ob-
tained results and suggesting possible future work.
2 PRELIMINARIES
2.1 Network Terminology
In order to have a well defined and coherent network
terminology throughout the paper, we first review the
main concepts and introduce some notation that will
be used on the following sections.
A network can be modeled as a graph G com-
posed of the set V (G) of vertices or nodes and the
set E(G) of edges or connections. The size of a graph
is the number of vertices and is written as |V (G)|. A
k-graph is graph of size k. The neighborhood of a ver-
tex u ∈ V (G), denoted as N(u), is composed by the set
of vertices v ∈ V (G) that are adjacent to u (u is not in-
cluded). All vertices are assigned consecutive integer
numbers starting from 0, and the comparison v < u
means that the index of v is lower than that of u.
A subgraph G
k
of a graph G is a graph of size k
in which V (G
k
)⊆V (G) and E(G
k
)⊆E(G). This sub-
graph is said to be induced if for any pair of ver-
tices u and v of V (G
k
), (u, v) is an edge of G
k
if
and only if (u, v) is an edge of G. The neighborhood
of a subgraph G
k
, denoted by N(G
k
) is the union of
N(u) for all u ∈ V (G
k
). The exclusive neighborhood
of a vertex u relative to a subgraph G
k
is defined as
N
excl
(u,G
k
) = {v ∈ N(u) : v /∈ G
k
∪ N(G
k
)}.
A mapping of a graph is a bijection where each
vertex is assigned a value. Two graphs G and H are
said to be isomorphic if there is a one-to-one map-
ping between the vertices of both graphs where two
vertices of G share an edge if and only if their corre-
sponding vertices in H also share an edge.
2.2 Subgraph Census
We give a rigorous definition for the subgraph census
problem:
Definition 1 (k-subgraph Census). A k-subgraph
census of a graph G is determined by the exact count
of all occurrences of isomorphic induced subgraph
classes of size k in G, where k ≤ |V (G)|.
Note that this definition is very broad and can be
applied to all kinds of networks, whether they are di-
rected or undirected, colored or not and weighted or
unweighted. Also note that here, unlike in (Kashtan
et al., 2004), we are concerned with an exact result
and not just an approximation.
A crucial concept that we have not yet completely
defined is how to distinguish two different occur-
rences of a subgraph. Given that we are only inter-
ested in finding induced subgraphs, we can allow an
arbitrary overlap of vertices and edges or have some
constraints such as no edge or vertex sharing by two
occurrences. The several possibilities that we can
have for the frequency are considered and discussed
in (Schreiber and Schwobbermeyer, 2004). Here we
focus on the most widely used definition that we for-
malize next:
Definition 2 (Different occurences of k-subgraphs).
Two occurrences of subgraphs of size k, in a graph G,
are considered different if they have at least one vertex
PARALLEL CALCULATION OF SUBGRAPH CENSUS IN BIOLOGICAL NETWORKS
57

or edge that they do not share. All other vertices and
edges can overlap.
Note that this has a vital importance on the num-
ber of subgraphs we find and consequently to the
tractability of the problem.
2.3 Related Work
There exists a vast amount of work on graph min-
ing. Particularly, the field of frequent subgraph min-
ing has been very prolific, producing sequential al-
gorithms like Gaston (Nijssen and Kok, 2004). Al-
though related, these algorithms differ substantially
in concept from our approach since their goal is to
find the most frequent subgraphs that appear in a set
of graphs, while we try to find the frequency of all
subgraphs on a single graph.
Regarding subgraph census itself, most of the
work on social networks is based on small sized sub-
graphs - mostly triads (Wasserman et al., 1994; Faust,
2007) - and therefore does not focus on efficiency, but
rather on the interpretation of the results. However,
for network motifs, efficiency does play an important
role and much importance is given to the algorithm for
generating the census. Increasing the speed may lead
to detection of bigger patterns and even an increase
in size of just one can yield scientifically important
results because a new previously unseen pattern with
functional significance may be discovered.
The three best known production tools for find-
ing motifs are all based on serial algorithms.
Mfinder (Milo et al., 2002) was the first and it is based
on a recursive backtracking algorithm that generates
all k-subgraphs. It may generate the same subgraph
several times because it initiates a search procedure
in each of its nodes. Fanmod (Wernicke, 2006) uses
an improved algorithm called ESU, that only allows
searches being initiated on the nodes with an index
higher than the root node and therefore each subgraph
is found only once. MAVisto (Schreiber and Schwob-
bermeyer, 2004) does not improve efficiency except
when it uses a different concept for frequency.
Work on parallel algorithms for subgraph census
is scarce. Wang and Parthasarathy (2004) propose an
algorithm for finding frequent subgraphs but do not
count all of them. Schatz et al. (2008) focuses on net-
work motifs and how to parallelize queries of indi-
vidual subgraphs and not on how to enumerate all of
them.Wang et al. (2005) takes the closest approach to
our work. Their algorithm relies on finding a neigh-
borhood assignment for each node that avoids overlap
and redundancy on subgraph counts, as in Wernicke
(2006), and tries to statically balance the workload
“a priori” based only on each node degree (no details
are given on how this is done and how it scales). An-
other distinctive characteristic of their approach is that
they do not do isomorphism tests during the parallel
computation, they wait until the end to check all the
subgraphs and compute the corresponding isomorphic
classes. As we will see, our approach differs signif-
icantly from this one as it contributes with dynamic
and adaptive strategies for load balancing, thus attain-
ing higher efficiency.
3 PARALLEL ALGORITHMS
3.1 Core Sequential Unit
Given that we are interested in having an exact count
of all classes of isomorphic subgraphs, we must enu-
merate all subgraphs. The ESU algorithm (Wernicke,
2006) is a key component of the fastest network mo-
tif tool available and as far as we know it is one of
the most efficient algorithms for subgraph enumera-
tion. Thus we chose the ESU algorithm as our starting
point and modified its recursive part to create a proce-
dure that given a graph G, a size k, a vertex minimum
index min, a partially constructed subgraph G
subgraph
,
and a list of possible extension nodes V
ext
, enumerates
all k-subgraphs that contain G
subgraph
and no nodes
with index lower than min. This procedure is depicted
in algorithm 1. It recursively extends the subgraph
G
subgraph
by first adding the new node u. If the new
subgraph has size k, then it determines a unique iden-
tification and saves it in a dictionary. Otherwise, it
expands the set of possible extension nodes, V
ext
, with
the nodes that are in the exclusive neighborhood of u
relative to the subgraph G
subgraph
and also satisfy the
property of being numerically bigger then min. If the
extension set of nodes is not null then a new node is
removed from extended V
ext
and recursion is made.
Algorithm 1 Extending a partially enumerated subgraph.
1: procedure EXTEND(G, k,min,u,G
subgraph
,V
ext
)
2: G
0
subgraph
← G
subgraph
∪ {u}
3: if |V(G
0
subgraph
)| = k then
4: str ← CanonicalString(G
0
subgraph
)
5: Dictionary.AddAndIncrement(str)
6: else
7: V
0
ext
←V
ext
∪{v∈N
excl
(u,G
subgraph
) : v > min}
8: while V
0
ext
6=
/
0 do
9: Remove an arbitrarily chosen v ∈ V
0
ext
10: Extend(G,k,min,v, G
0
subgraph
,V
0
ext
)
Calling
Extend(
G
,
k
,
u
,
u
,
{}
,
{}
)
for every u ∈
V (G) is exactly the equivalent to the original ESU al-
gorithm. Therefore, as long as we call it on all nodes,
BIOINFORMATICS 2010 - International Conference on Bioinformatics
58

we can be certain that it will produce complete results,
as shown in (Wernicke, 2006). Moreover,
Extend()
guarantees that each existent subgraph will only be
found once on the call of its lowest index, as exem-
plified in figure 1. This avoids redundant calculations
as in (Wang et al., 2005) and is crucial to achieve an
efficient census.
Figure 1: Example of how
Extend()
calls generate all sub-
graphs.
Before going into the details of the parallelism
two additional notes are needed. First, isomorphism
(line 4 of the procedure) is taken care of by using the
canonical string representation of the graphs, defined
as the concatenation of the elements of the adjacency
matrix of the canonical labeling. In our case we use
McKay’s nauty algorithm (McKay, 1981), a widely
known fast and practical implementation of isomor-
phism detection. Second, in order to store the results
found within one call to our procedure (line 5), we
use a string dictionary structure. This can be imple-
mented in many ways, for example using an hash ta-
ble or a balanced red-black tree. We implement the
later (using STL map from C++).
3.2 Initial Parallel Approaches
Each of the aforementioned calls to
Extend(
G
,
k
,
u
,
u
,
{}
,
{}
)
is completely inde-
pendent from each other and we call it a primary
work unit. A possible way of parallelizing subgraph
census is then to distribute these work units among
all CPUs
1
. The problem is that these units have
a computational cost with a huge variance, as the
inherent substructure and the number of subgraphs
each one enumerates are also quite different.
We experimented several strategies for the distri-
bution in order to obtain the desired load balance. The
first one was to statically allocate the units to workers
before starting the census computation. In order to
obtain good results this would need accurate estimates
of the time that each unit takes to compute. We were
unable to do that with the desired accuracy, since cal-
1
from now on we will refer to processors in computa-
tional nodes as CPUs or workers to avoid confusion be-
tween them and graph nodes.
culating this is almost as difficult as enumerating the
subgraphs themselves.
We then took the path of a more dynamic ap-
proach using a master-worker architecture (Heymann
et al., 2000). The master maintains a list of unpro-
cessed primary work units. Workers ask the master
for a unit, process it and repeat until there is noth-
ing more to compute. Each worker maintains its own
dictionary of frequencies. When all work units have
been computed the master is responsible for collect-
ing and merging all results, summing up the frequen-
cies found.
The position of the work units on the master’s list
will determine the total time needed and we tried sev-
eral strategies. Initially we just added all work units
to the list in chronological order of the nodes. This
proved to be a bad strategy since it is the same as a
random assignment, which is in principle the worst
possible (Heymann et al., 2000). We then experi-
mented giving the work units sorted to an estimated
cost, using LPTF (Largest Processing Time First)
strategy. If the estimate was perfect, it is known that
we would achieve at least
3
4
of the optimum (Hall,
1997). We only had an approximation (based on
the number of nodes achievable in k − 1 steps) and
therefore that boundary is not guaranteed. However,
since our heuristic function maintained a reasonable
ordering of the nodes, the performance was vastly im-
proved.
We still had the problem that the call to a few
primary work units (potentially even just one) could
consume almost all the necessary compute time. This
prevents good load balance strategies, given that each
work units runs sequentially. This problems occurs
very often in reality because typical complex net-
works are scale free (Barabasi and Albert, 1999).
Whenever their hubs are the starting nodes of a work
unit, very large neighborhoods are induced and a huge
amount of subgraphs is generated. No matter what
we do, there will always be a worker computing the
largest sequential work unit and therefore the total
compute time needed cannot be smaller than that.
On some of our experiments with real biological net-
works, this largest atomic unit could consume more
than 25% of the total execution time, which limits our
scalability.
Considering that a work unit only calculates sub-
graphs containing nodes with indices greater than the
index of the initial node, we devised a novel strategy
in which we give higher index numbers to the poten-
tially more time consuming nodes (those with larger
degrees). We expected this to reduce the number of
subgraphs spawning from these nodes, thus reducing
the granularity of the work units induced by those
PARALLEL CALCULATION OF SUBGRAPH CENSUS IN BIOLOGICAL NETWORKS
59
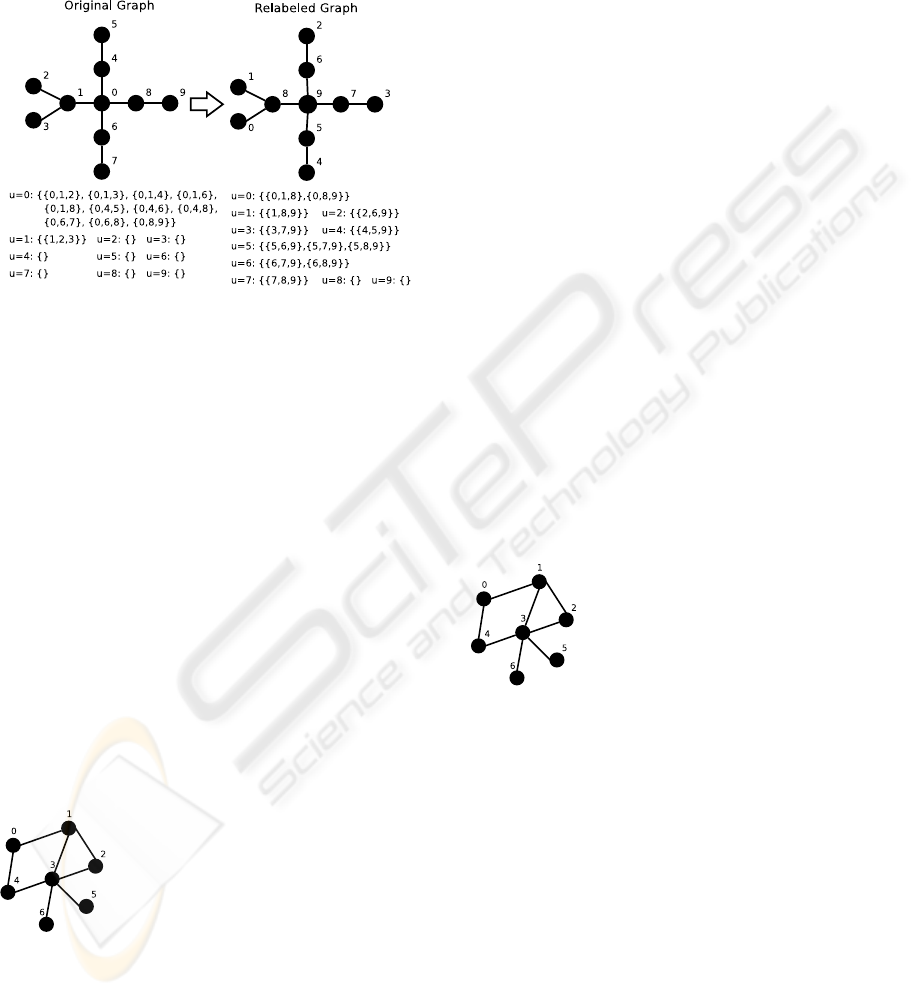
nodes. To accomplish this strategy, we implemented
a node relabeling algorithm in which the nodes are
sorted increasingly by their degree. Figure 2 gives a
practical example of this strategy at work, producing
a more balanced graph.
Figure 2: Relabeling the graph to balance primary work
units.
Although this last approach improved our results,
we expected that for some networks the relabeling
strategy could not reduce enough the granularity of
the work units, thus preventing scalability. We felt
that we really needed a strategy that could divide the
work units further.
3.3 Adaptive Parallel Enumeration
By inspecting the computation flow of a primary work
unit, we can observe that there are several recursive
calls to
Extend()
, as exemplified in figure 3 (for sim-
plicity, we do not show G and k since these are fixed
arguments).
Extend(
0
,
0
,
{}
,
{}
)
V
0
ext
= {1,4}
Extend(
0
,
1
,
{0}
,
{4}
)
V
0
ext
= {2,3,4}
Extend(
0
,
2
,
{0,1}
,
{3,4}
)
→ Found subgraph {0,1,2}
Extend(
0
,
3
,
{0,1}
,
{4}
)
→ Found subgraph {0,1,3}
Extend(
0
,
4
,
{0,1}
,
{}
)
→ Found subgraph 0,1,4
Extend(
0
,
4
,
{0}
,
{}
)
V
0
ext
= {3}
Extend(
0
,
3
,
{0,4}
,
{}
)
→ Found subgraph 0,3,4
Figure 3: The computation flow of a primary work unit.
With our formulation of
Extend()
, all recursive
calls are independent with no need for information of
previous data on the recursion stack besides the argu-
ments it was called with. One way to divide a primary
work unit is therefore to partitionate it in its recursive
calls. A tuple (min, u,G
subgraph
,V
ext
) completely de-
fines the resulting call to
Extend()
and we will now
call work unit to a tuple like this, with primary work
units being only a particular case.
Our new strategy to reduce the granularity of the
work units uses a threshold parameter to indicate the
point in the computation at which we split the ex-
ecution of the current work unit into smaller work
units. Instead of really computing subsequent recur-
sive calls, we encapsulate their arguments into new
smaller work units and send them to the master to be
added to the list of unprocessed work, effectively di-
viding our previously atomic sequential units. This
leads to a simpler, yet elegant, solution when com-
pared to more common adaptive strategies that need a
queue in each computation node (Eager et al., 1986).
Figure 4 illustrates our strategy at work. Remem-
ber that the new work units are still independent and
we do not need to be concerned with locality. All
subgraphs will be found and added to the respective
worker’s dictionary of frequencies, being merged in
the end of the whole computation to determine the
global resulting census.
Extend(
0
,
0
,
{}
,
{}
)
V
0
ext
= {1,4}
Extend(
0
,
1
,
{0}
,
{4}
)
V
0
ext
= {2,3,4}
Extend(
0
,
2
,
{0,1}
,
{3,4}
)
→ Found subgraph {0,1,2}
——– Splitting Threshold ——–
Extend(
0
,
3
,
{0,1}
,
{4}
)
⇒ New work unit with these arguments
Extend(
0
,
4
,
{0,1}
,
{}
)
⇒ New work unit with these arguments
Extend(
0
,
4
,
{0}
,
{}
)
⇒ New work unit with these arguments
Figure 4: Work split strategy for work units.
Our algorithm is able to adjust itself during exe-
cution using this division strategy. It splits large work
units into new smaller work units ensuring that their
grain-size will never be larger than the size of work
units executed up to the threshold value. In doing so,
we are able to improve the load balancing and thus
achieve an effective dynamic and adaptive behavior.
The splitting threshold parameter is central in our
adaptive algorithm. If it is set too high, the work units
will not be sufficiently divided in order to adequately
balance the work among all CPUs. If it is too low,
work will be divided too soon and the communication
costs will increase. As a proof of concept our cur-
BIOINFORMATICS 2010 - International Conference on Bioinformatics
60
rent implementation uses a threshold that limits the
computation time spent on a work unit to a maximum
value, but other measures could be used like for ex-
ample the number of subgraphs already enumerated.
One aspect not yet discussed, but that is orthogo-
nal to all discussed strategies, concerns the aggrega-
tion of results at the master. If a naive approach was
taken, then each worker would be sending their results
to the master sequentially. This would be highly in-
efficient and therefore we devised a parallel approach
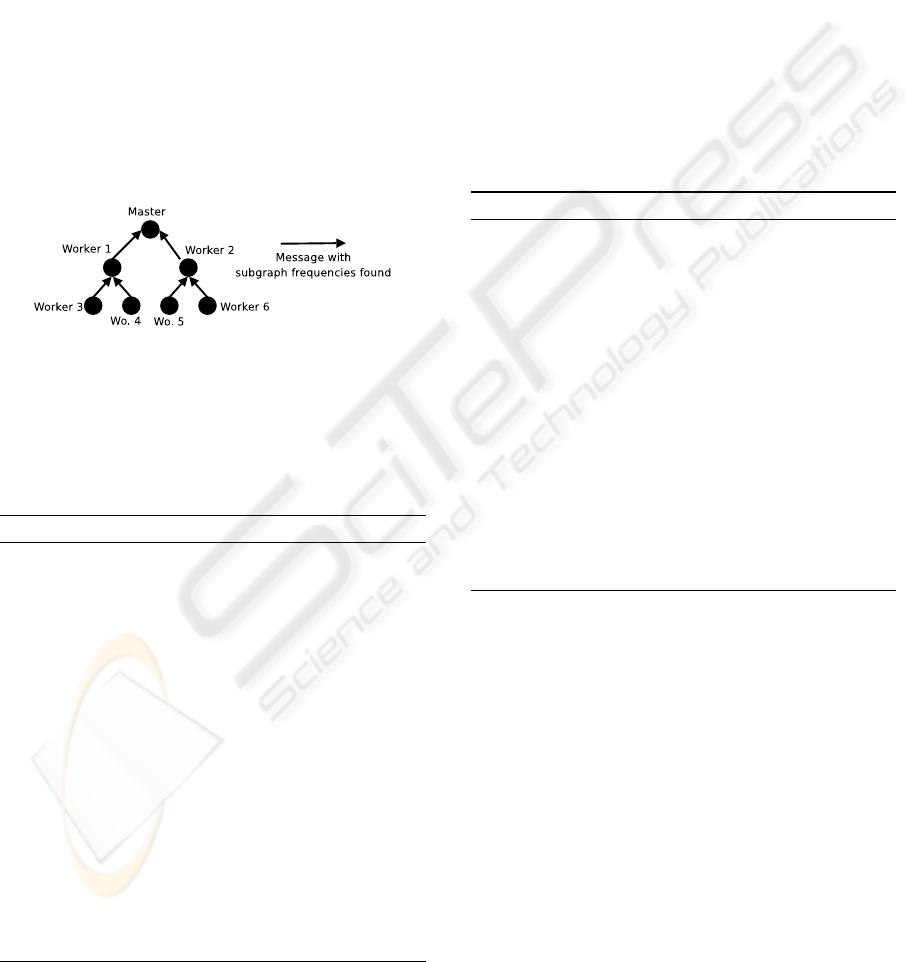
for this final step. We use an hierarchical binary tree
to organize the aggregation of results, where each
worker receives the results of two other child workers,
updates its own frequency dictionary accordingly, and
then in turn sends the aggregated results to its parent.
This is exemplified in figure 5 and has the potential
to logarithmically reduce the total time needed to ac-
complish this step.
Figure 5: Example of results aggregation with 1 master and
6 workers.
All the ideas described are the basis for our main
algorithm that we called Adaptive Parallel Enumera-
tion (APE). Algorithms 2 and 3 describe in detail our
APE master and worker procedures.
Algorithm 2 APE master node.
1: procedure MASTER(G,k)
2: L
WorkUnits
.add(AllPrimaryWorkUnits)
3: while CPUsWorking 6=
/
0 do
4: msg ← ReceiveMessage(AnyWorker)
5: if msg.type = RequestForWork then
6: if L
WorkUnits
.notEmpty() then
7: W ← L
WorkUnits
.pop()
8: newMsg ← EncapsulateWorkUnit(W )
9: SendMessage(msg.Sender,newMsg)
10: else
11: IdleWorkers.push(msg.Sender)
12: else if msg.type = NewWorkUnit then
13: if IdleWorkers.notEmpty() then
14: worker ← IdleWorker.pop()
15: SendMessage(worker,msg)
16: else
17: W ← ExtractWorkUnit(msg)
18: L
WorkUnits
.push(W)
19: BroadcastMessage(Terminate);
20: ReceiveResults(Le f tChild,RightChild)
The master starts by adding all primary work units
to the list of unprocessed work units (L
WorkUnits
).
Then starts its main cycle where it waits for a mes-
sage from a worker. If the message indicates that the
worker needs more work, the master sends it the next
unprocessed work unit L
WorkUnits
. If the list is empty,
the master signals the worker as being idle. If the mes-
sage indicates that the worker is splitting work and
thus sending a new unprocessed work unit, then the
master adds that new work unit to L
WorkUnits
. If there
is an idle worker, then this unit is sent right away to
that worker. When all workers are idle, the subgraph
enumeration is complete and the master ends its main
cycle, broadcasting to all workers that event. What
remains is then to collect the results and following the
explained hierarchical aggregation process, the mas-
ter receives the results of two workers and merges
them in an unified global dictionary of the frequen-
cies of each isomorphic class of k-subgraphs.
Algorithm 3 APE worker node.
1: procedure WORKER(G,k)
2: while msg.type 6= Terminate do
3: msg ← ReceiveMessage(Master)
4: if msg.type = NewWorkUnit then
5: W = (G, k, min, u,G
subgraph
,V
ext
) ←
ExtractWorkUnit(msg)
6: Extend’(W)
7: ReceiveResults(Le f tChild,RightChild)
8: SendResults(ParentWorker)
9: procedure EXTEND’(W)
10: if SplittingThresholdAchieved() then
11: msg ← EncapsulateWorkUnit(W)
12: SendMessage(Master,msg)
13: else
14: lines 2 to 9 of algorithm 1
15: Extend’(W
0
= (G,k, min,v, G
0
subgraph
,V
0
ext
))
16: lines 11 and 12 of algorithm 1
The worker has a main cycle where it waits for
messages from the master. If the message signals a
new work unit to be processed, than it calls a mod-
ified version of the
Extend()
procedure to compute
that work unit. If the message signals termination,
then it exits the cycle, receiving and merging the re-
sults from two other workers with its own dictionary.
It then send those results to a single parent processor,
that depending on the worker rank number may be
other worker or the master itself, completing the hi-
erarchical aggregation phase. Regarding the modified
version of the
Extend()
procedure, it is exactly the
same as the version depicted on algorithm 1 except
the fact than when the splitting threshold is achieved,
the computation is stopped and all subsequent calls
consist now in encapsulating the arguments into a new
work unit and sending it to the master.
There are two issues that we would like to clarify.
PARALLEL CALCULATION OF SUBGRAPH CENSUS IN BIOLOGICAL NETWORKS
61
Table 1: Networks used for experimental testing of the algorithms.
Network Nodes Edges Avg. Degree Description
Neural
297 2345 7.90 Neural network of C. elegans
Gene
688 1079 1.57 Gene regulation network of S. cerevisiae
Metabolic
1057 2527 2.39 Metabolic network of S. pneumoniae
Protein
2361 7182 3.04 Protein-protein interaction network of S. cerevisiae
First, we decided to use a dedicated master because
it is a central piece in the architecture and we needed
the highest possible throughput in the assignment of
new work units to idle workers. Second, APE was
originally created having in mind homogeneous re-
sources but its dynamic and adaptive design makes it
also suited for heterogeneous environments.
4 RESULTS
All experimental results were obtained on a dedicated
cluster with 12 SuperMicro Twinview Servers for a
total of 24 nodes. Each node has 2 quad core Xeon
5335 processors and 12 GB of RAM, totaling 192
cores, 288 GB of RAM, and 3.8TB of disk space, us-
ing Infiniband interconnect. The code was developed
in C++ and compiled with gcc 4.1.2. For message
passing we used OpenMPI 1.2.7. All the times mea-
sured were wall clock times meaning real time from
the start to the end of all processes.
In order to evaluate our parallel algorithms we
used four different representative biological networks
from different domains:
Neural
(Watts and Strogatz,
1998),
Gene
(Milo et al., 2002),
Metabolic
(Jeong
et al., 2000) and
Protein
(Bu et al., 2003). The
networks present varied topological features that are
summarized in Table 1.
We first studied the computational behaviour of
each network using the equivalent to the ESU al-
gorithm, sequentially calling all primary work units
(with no MPI overhead). This measures how much
time a serial program would take to calculate a sub-
graph census. We took note of what was the maxi-
mum possible subgraph size k achievable in a reason-
able amount of time (we chose one hour as the max-
imum time limit). We calculated the average growth
ratio, that is, by which factor did the execution time
grew up as we increased k by one. Finally, we also
calculated the total number of different occurrences
of k-subgraphs and the number of different classes of
isomorphism found on those subgraphs. The results
obtained can be seen in table 2.
Note the relatively small subgraph sizes achiev-
able. This is not caused by our implementation, since
using the FANMOD tool (Wernicke, 2006), the fastest
Table 2: Maximum achievable subgraph sizes k using a se-
rial program.
Network k
Time Average Total nr of Isomor.
spent (s) Growth subgraphs classes
Neural
6 10,982.9 47.6±0.4 1.3 × 10
10
286,376
Gene
7 4,951.0 19.0±1.4 4.2 × 10
9
4,089
Metabolic
6 14,000.1 46.5±2.7 1.9 × 10
10
1,696
Protein
6 10,055.2 31.2±3.1 1.3 × 10
10
231,620
available for network motifs calculation, we also were
only able to achieve the same maximum k in one hour.
The cause is that, as expected, the computing time
grows exponentially as the subgraph size increases.
We also observe that although different graphs present
very different average growths, the growth rate for a
given graph seems fairly constant (note the standard
deviation).
For the next set of results we decided to fix the
respective k for each graph to the values depicted in
table 2, in order to have more comparable results.
We evaluated the parallel strategies described in sec-
tion 3. We compared the speedup obtained on all
three graphs for the dynamic strategy with chrono-
logical order in the work units list (DYN-CRON),
with LPTF ordering (DYN-LPTF), with graph rela-
beling followed by LPTF (DYN-RELABEL) and fi-
nally with the APE strategy.
For the APE algorithm it is necessary to explain
how we chose the value for the splitting threshold pa-
rameter. We chose to employ the time spent in the
same work unit as a proof of concept for the useful-
ness of APE and we empirically experimented several
values for this time limit, reducing it while verifying
that the speedup was being improved. This value con-
trols the granularity of the work units. We want it as
small as possible, as long as the increase in communi-
cation costs does not overcome the effect of increased
sharing. We found that for our context 2 seconds ap-
peared to be a good and balanced value (the time spent
in communications during the enumeration of the sub-
graphs was always smaller than 2% of the total time
spent), and we measured the speedup with that partic-
ular value chosen as the threshold (APE-2s).
We used a minimum of 8 CPUs because each com-
putation node in the cluster had precisely that number
of processors. With less CPUs the nodes would not
BIOINFORMATICS 2010 - International Conference on Bioinformatics
62

Table 3: Detailed APE behavior with splitting threshold set to 2s.
Network k
#CPUs: speedup (% time spent in aggregating results)
8 16 32 64 128
Neural
6 7.0 (0.2%) 14.8 (1.2%) 30.1 (3.4%) 58.7 (8.0%) 107.0 (16.9%)
Gene
7 7.0 (0.1%) 15.0 (0.2%) 30.7 (0.4%) 62.0 (0.8%) 125.0 (0.7%)
Metabolic
6 6.9 (0.1%) 14.9 (0.1%) 30.8 (0.3%) 62.4 (0.6%) 125.5 (1.3%)
Protein
6 6.6 (0.2%) 13.7 (1.2%) 28.0 (3.3%) 54.6 (7.4%) 96.9 (18.8%)
be exclusively dedicated to the subgraph census. The
results obtained up to 128 processors are depicted in
figure 6. The results obtained clearly show different
performance levels for the different strategies. Gener-
ally speaking, the strategies based on the atomic pri-
mary work units do not scale well, although the in-
cremental strategies used show some improvements
in the speedup. Overall, as expected, the adaptive
strategy, APE-2s, outperforms all others and clearly
achieves scalability.
Figure 6: Speedups obtained with several parallel ap-
proaches.
Next, we further analyze the performance of APE-
2s on all networks. Table 3 details the performance of
the APE-2s up to 128 processors, and show the per-
centage of time spent in the final step of aggregating
all frequency results in the master CPU.
We can observe that for
Gene
and
Metabolic
,
APE-2s obtains almost perfect linear speedup, with
a reduced amount of time spent in the aggregation
phase. In
Neural
and
Protein
, despite the good re-
sults, there is still some room for improvement. The
time spent communicating the results in the end of the
computation, more than 15% of the execution time
with 128 processors, is the cause for the loss in the
speedup. In fact, with more than 200,000 classes of
isomorphic subgraphs in the network (see table 2),
each worker has to communicate all of the frequen-
cies it finds in its respective computation. On aver-
age, the number of different classes of isomorphism
discovered on the same CPU, is larger than 150,000.
Each of these classes has to be encapsulated (uniquely
identifying the class) in order for the receiver to be
able to decode it and merge the results. Even with our
hierarchical method for aggregating the results, this
still takes a considerable amount of time. This effect
is not so noticeable in the other networks since the
number of different classes found is much lower (due
to inherent network topology, with a smaller average
degree per node).
As a final demonstration of the relevance of our al-
gorithm, consider the average growth as we increase
k (shown in Table 2). As long as the number of pro-
cessors we have available is larger than the average
growth, we should be able to compute the (k + 1)-
census in the same amount of time we initially were
able to compute the k-census sequentially. For exam-
ple, using the average growth, we can estimate that
calculating a 7-census of
Metabolic
would take more
than one week, if done sequentially. Using 128 pro-
cessors and APE-2s, we were able to calculate it in
less than 1h30m, spending even less than half of the
time a sequential 6-census takes.
5 CONCLUSIONS
We presented several strategies for calculating sub-
graph census of biological networks in parallel. Our
approaches are based on an efficient sequential al-
gorithm called ESU that we parallelized by initially
modifying it to a version capable of producing inde-
pendent and dividable work units. We started with
a dynamic master-worker strategy and subsequently
improved it with an LPTF order of processing and a
smart relabeling of the nodes in the graph. We also
PARALLEL CALCULATION OF SUBGRAPH CENSUS IN BIOLOGICAL NETWORKS
63

presented APE, a novel adaptive load balancing al-
gorithm, which includes an hierarchical aggregation
of the results found in each worker. APE proved to
be an acceptable and scalable solution for the set of
representative networks studied, successfully reduc-
ing the time needed to calculate the subgraph census
and achieving larger subgraph sizes than were before
possible.
The main drawback of APE seems to be the fi-
nal aggregation of results. We plan to research and
improve this step in the future. One way of doing it
would be to use a more compact and compressed rep-
resentation of the results. We also plan to research
the splitting threshold parameter in order to better un-
derstand on what does it depend, exactly how does it
affect the computation and how could it be automati-
cally determined by the algorithm. We are collaborat-
ing with neuroinformatics scientists in order to apply
the described strategies on real neural networks to ob-
tain new and interesting results on previously unfea-
sible subgraph census.
ACKNOWLEDGEMENTS
We thank Enrico Pontelli for the use of Inter Clus-
ter in the New Mexico State University. Pe-
dro Ribeiro is funded by an FCT Research Grant
(SFRH/BD/19753/2004). This work was also par-
tially supported by project CALLAS of the FCT (con-
tract PTDC/EIA/71462/2006).
REFERENCES
Albert, I. and Albert, R. (2004). Conserved network mo-
tifs allow protein-protein interaction prediction. Bioin-
formatics, 20(18):3346–3352.
Alm, E. and Arkin, A. P. (2003). Biological networks. Cur-
rent Opinion in Structural Biology, 13(2):193–202.
Barabasi, A. L. and Albert, R. (1999). Emergence of scaling
in random networks. Science, 286(5439):509–512.
Bordino, I., Donato, D., Gionis, A., and Leonardi, S.
(2008). Mining large networks with subgraph counting.
In Procs of the 8th IEEE International Conference on
Data Mining (ICDM), pages 6 pp.+.
Bu, D., Zhao, Y., Cai, L., Xue, H., Zhu, X., Lu, H., Zhang,
J., Sun, S., Ling, L., Zhang, N., Li, G., and Chen, R.
(2003). Topological structure analysis of the protein-
protein interaction network in budding yeast. Nucl. Acids
Res., 31(9):2443–2450.
Costa, L., Rodrigues, F. A., Travieso, G., and Boas, P. R. V.
(2007). Characterization of complex networks: A survey
of measurements. Advances In Physics, 56:167.
Eager, D. L., Lazowska, E. D., and Zahorjan, J. (1986).
Adaptive load sharing in homogeneous distributed sys-
tems. IEEE Trans. Softw. Eng., 12(5):662–675.
Faust, K. (2007). Very local structure in social networks.
Sociological Methodology, 37(1):209–256.
Hall, L. A. (1997). Approximation algorithms for schedul-
ing. In Approximation algorithms for NP-hard problems,
pages 1–45, Boston, MA, USA. PWS Publishing Co.
Heymann, E., Senar, M. A., Luque, E., , and Livny, M.
(2000). Evaluation of an adaptive scheduling strategy
for master-worker applications on clusters of worksta-
tions. In Proc. of the 7th International Conference on
High Performance Computing, Bangalore, India.
Itzkovitz, S., Levitt, R., Kashtan, N., Milo, R., Itzkovitz,
M., and Alon, U. (2005). Coarse-graining and self-
dissimilarity of complex networks. Phys Rev E Stat Non-
lin Soft Matter Phys, 71(1 Pt 2).
Jeong, H., Tombor, B., Albert, R., Oltvai, Z. N., and
Barab
´
asi, A. L. (2000). The large-scale organization of
metabolic networks. Nature, 407(6804):651–654.
Kashtan, N., Itzkovitz, S., Milo, R., and Alon, U. (2004).
Efficient sampling algorithm for estimating subgraph
concentrations and detecting network motifs. Bioinfor-
matics, 20(11):1746–1758.
Kondoh, M. (2008). Building trophic modules into a per-
sistent food web. Proceedings of the National Academy
of Sciences, 105(43):16631–16635.
Kuramochi, M. and Karypis, G. (2001). Frequent subgraph
discovery. IEEE International Conference on Data Min-
ing, 0:313.
Matias, C., Schbath, S., Birmel, E., Daudin, J.-J., and
Robin, S. (2006). Network motifs: mean and variance
for the count. REVSTAT, 4:31–35.
Mazurie, A., Bottani, S., and Vergassola, M. (2005). An
evolutionary and functional assessment of regulatory net-
work motifs. Genome Biology, 6:R35.
McKay, B. (1981). Practical graph isomorphism. Congres-
sus Numerantium, 30:45–87.
Middendorf, M., Ziv, E., and Wiggins, C. (2004). Infer-
ring network mechanisms: The drosophila melanogaster
protein interaction network. PNAS, 102:3192.
Milo, R., Shen-Orr, S., Itzkovitz, S., Kashtan, N.,
Chklovskii, D., and Alon, U. (2002). Network motifs:
simple building blocks of complex networks. Science,
298(5594):824–827.
Nijssen, S. and Kok, J. N. (2004). Frequent graph mining
and its application to molecular databases. In SMC (5),
pages 4571–4577. IEEE.
Picard, F., Daudin, J.-J. J., Koskas, M., Schbath, S., and
Robin, S. (2008). Assessing the exceptionality of net-
work motifs. J Comput Biol.
Schatz, M., Cooper-Balis, E., and Bazinet, A. (2008). Par-
allel network motif finding.
Schreiber, F. and Schwobbermeyer, H. (2004). Towards mo-
tif detection in networks: Frequency concepts and flexi-
ble search. In Proceedings of the International Workshop
on Network Tools and Applications in Biology (NET-
TAB04, pages 91–102.
BIOINFORMATICS 2010 - International Conference on Bioinformatics
64

Sporns, O. and Kotter, R. (2004). Motifs in brain networks.
PLoS Biology, 2.
Valverde, S. and Sol
´
e, R. V. (2005). Network motifs in com-
putational graphs: A case study in software architecture.
Physical Review E (Statistical, Nonlinear, and Soft Mat-
ter Physics), 72(2).
Wang, C. and Parthasarathy, S. (2004). Parallel algorithms
for mining frequent structural motifs in scientific data.
In In ACM International Conference on Supercomputing
(ICS) 2004.
Wang, T., Touchman, J. W., Zhang, W., Suh, E. B., and Xue,
G. (2005). A parallel algorithm for extracting transcrip-
tion regulatory network motifs. Bioinformatic and Bio-
engineering, IEEE International Symposium on, 0:193–
200.
Wasserman, S., Faust, K., and Iacobucci, D. (1994). Social
Network Analysis : Methods and Applications (Struc-
tural Analysis in the Social Sciences). Cambridge Uni-
versity Press.
Watts, D. J. and Strogatz, S. H. (1998). Collective dynamics
of ’small-world’ networks. Nature, 393(6684):440–442.
Wernicke, S. (2006). Efficient detection of network mo-
tifs. IEEE/ACM Trans. Comput. Biol. Bioinformatics,
3(4):347–359.
PARALLEL CALCULATION OF SUBGRAPH CENSUS IN BIOLOGICAL NETWORKS
65
