
LINEAR–TIME MATCHING OF POSITION WEIGHT MATRICES
Nikola Stojanovic
Department of Computer Science and Engineering, University of Texas at Arlington, Arlington, TX 76019, U.S.A.
Keywords:
DNA motifs, Position weight matrices, Genome–wide analysis, Algorithms, Genomics, Pattern matching.
Abstract:
Position Weight Matrices are a popular way of representing variable motifs in genomic sequences, and they
have been widely used for describing the binding sites of transcriptional proteins. However, the standard
implementation of PWM matching, while not inefficient on shorter sequences, is too expensive for whole–
genome searches. In this paper we present an algorithm we have developed for efficient matching of PWMs
in long target sequences. After the initial pre–processing of the matrix it performs in time linear to the size of
the genomic segment.
1 INTRODUCTION
Eukaryotic genes are generally regulated in com-
plex ways, through networks of protein–DNA and
protein–protein interactions, which direct chromatin
remodeling, histone modifications, formation of tran-
scriptional initiation complexes and RNA Polymerase
elongation. The prevailing opinion, corroborated by
some studies (Khambata-Ford et al., 2003; Young
et al., 2003) but being increasingly questioned (Nel-
son et al., 2004; The ENCODE Project Consortium,
2007; Stojanovic, 2009) is that most of these interac-
tions take place within a few hundred bases upstream
of the transcription start sites. Even as regions im-
portant for the regulation of genes have been found
at distal loci, around alternative first exons, in introns
and sequences located downstream of the transcrip-
tion start sites or even genes themselves, core pro-
moter sites are still considered the most important for
the gene expression. It is also generally accepted that
the binding of transcriptional enzymes is in large part
directed by specific motifs in DNA sequence. How-
ever, while there are proteins which bind only to exact
layouts of bases, most transcription factors are rather
non-specific in their choice of a binding site.
Consequently, the search for transcription factor
binding sites has become one of the most popular sub-
fields of bioinformatics, and many algorithms have
been developed over about two decades of intensive
research. The early approaches relied on a rather
naive assumption that the motifs at the target sites
of proteins must feature information content suffi-
cient for their recognition, but disillusionment soon
followed, as any attempt to isolate these and other
functional elements in DNA following this logic re-
sulted in a very large number of false positives. Re-
cent methods have thus concentrated on the incorpo-
ration of additional information to the raw sequence
data, although they have so far neglected many impor-
tant biochemical aspects. The additional information
often relied on clustering of important motifs in pu-
tative regulatory modules, phylogenetic conservation
or matching the sequence to databases of experimen-
tally confirmed sites, such as TRANSFAC (Wingender,
2008) or Jaspar (Bryne et al., 2008).
Since many proteins important for transcriptional
regulation bind with low specificity, the experimen-
tally determined target motifs in DNA can be substan-
tially different. Nevertheless, they often feature a well
defined consensus sequence, with specific loci vary-
ing only marginally from the consensus. The extent of
that variation is usually captured by Position Weight
Matrices (PWMs), described in more detail below.
Briefly, the PWMs record the information about the
permissible variation of letters over the 4–letter DNA
alphabet, assigning a weight to each letter at each po-
sition in the motif in accordance with how often that
letter has been seen at that position within the exper-
66
Stojanovic N. (2010).
LINEAR–TIME MATCHING OF POSITION WEIGHT MATRICES.
In Proceedings of the First International Conference on Bioinformatics, pages 66-73
DOI: 10.5220/0002750500660073
Copyright
c
SciTePress

imentally determined binding sequences. The infor-
mation about functional motifs in DNA recorded in the
databases is nowadays usually in the form of PWMs,
and they can be used for searches in previously un-
characterized DNA fragments, for motifs sufficiently
similar to the consensus of a particular protein bind-
ing site. Over the years many programs have been
written for matching PWMs, including MATCH (Kel
et al., 2003) by the TRANSFAC database team, and
variants such as combinations of PWMs using mixture
model (Hannenhalli and Wang, 2005).
With the advances in microarray technology large
sets of putatively co-expressed genes became avail-
able, stimulating the development of methods to de-
tect conserved motifs in their upstream regions, such
as (Hughes et al., 2000), as well as the search for
putatively co-regulated genes by the identification of
shared regulatory modules, such as in (Qin et al.,
2003). It is intuitive that if a group of genes is co-
ordinately regulated, it should be controlled by simi-
lar sets of transcription factors. From the hypothesis
that protein binding is largely directed by target DNA
sequence motifs it follows that same (or similar) mo-
tifs should be present in regulatory sequences of co-
expressed genes, moreover as a cluster, or clusters.
Consequently, this led to further exploitation of motif
over-representation in sets of target sequences (Apos-
tolico et al., 2000; van Helden, 2004).
In the course of our work on the study of these
genomic environments, we have developed software
which extracts the most significant shared short (5–25
bases) approximate motifs found within the upstream
sequences (i.e. putative promoter regions) of genes
postulated to be co-expressed by microarray and
other experiments (Singh and Stojanovic, 2006). We
have recently expanded that work to genome–wide
searches for similar layouts, as reflected by conglom-
erations of a statistically significant number of motifs
previously discovered to be shared within the promot-
ers of a training set of co-expressed genes (Singh and
Stojanovic, 2009). Unfortunately, even as we were
able to record the consensus of the motifs of interest
in the form of PWMs, our genome–wide search had to
be executed using string representation (standing for
multiple exact patterns), since the current methods for
PWM matching are not efficient. When the matching
needs to be performed in limited environments repre-
senting gene upstream sequences, genomic domains
or gene clusters, naive approaches work well, how-
ever for whole–genome scans (having in mind that,
for instance, the human genome features more than
three billion bases) any performance worse than lin-
ear is not practical.
In this paper we describe an algorithm we have
devised to efficiently match patterns represented by
Position Weight Matrices. It relies on a somewhat ex-
pensive pre–processing step, however the cost of that
pre–processing is well compensated by the efficiency
gains once it is applied to whole–genome searches.
Before proceeding with the algorithm itself, in the
following chapter we shall present some basic ideas
governing the construction and use of the PWMs.
2 POSITION WEIGHT
MATRICES
If all sites where a same protein binds would feature
identical bases it would be a matter of simple pattern
matching to find them all. Unfortunately, for gene
regulatory proteins that is usually not the case, and
one has to deal with approximate matching, consen-
sus sequences and ambiguity codes. This is more than
a technical complication, as it introduces unreliability
to motif recognition. The ambiguity codes do not dis-
tinguish between the bases they stand for, so rare or
even impossible (concerning protein binding) combi-
nations of characters in the represented motifs may
match, leading to a large fraction of false positives.
On the other hand, if a character which infrequently
appears in the binding sequences is completely elim-
inated from the consensus, sites which do bind the
protein may be skipped, adding poor sensitivity to al-
ready compromised specificity. Furthermore, binding
motifs often contain irrelevant positions, and trying
to match any particular character at these loci would
obviously be futile.
A partial remedy to this problem can be an as-
signment of weights to characters of the consensus
sequence, so that for each position where more than
one base is possible there is a probability of occur-
rence associated with each choice. Stormo (Stormo,
1990) thus proposed a matrix–based approach, where
a position in a protein binding site is represented by a
column of a matrix, with one row for each nucleotide.
The guiding idea of the method was that if every char-
acter possible at a given position is assigned a score
such that the addition of scores for all positions pro-
vides an estimate about how close the sequence is
to the known protein binding site patterns, one can
decide whether to accept or reject the site based on
whether the total score is above or below a certain
predefined threshold. At any scanned sequence posi-
tion j aligned with matrix column i, a simple lookup
at the matrix entry at column i and row corresponding
to the letter found at j would then provide the score.
The threshold can be empirically determined
as the critical value of the ratio of probabilities
LINEAR--TIME MATCHING OF POSITION WEIGHT MATRICES
67

c)
TACACCG
TACACTG
TACACGG
TACACTG
GACACCG
TACACAG
TATACAG
GATACCG
TACACCG
TAGACAG 0 10 0 10 0 3 0
2 0 1 0 0 1 10
8 0 2 0 0 2 0
0 0 7 0 10 4 0
−−− 2.00 −−− 2.00 −−− 0.26 −−−
−−− −−− 1.49 −−− 2.00 0.68 −−−
−0.32 −−− −1.32 −−− −−− −1.32 2.00
1.68 −−− −0.32 −−− −−− −0.32 −−−
A
C
G
T
a) b)
Figure 1: An example of a Position Weight Matrix: a) A set of motifs on which the matrix is built; b) Letter counts at each
position in the motif, in matrix representation; c) Full matrix, obtained by taking log
2
of the probability of the character
occurrence at the position, divided by the general probability of the character, here assumed to be 0.25 for each of the ‘A’, ‘C’,
‘G’, ‘T’. ‘—’ indicates an infinitesimally small value.
P
F
(s)/P
G
(s), where s is the examined string, sub-
script F denotes that the probability is based on the
distribution of strings within the population of bind-
ing sites, and subscript G denotes that the probabil-
ity is based entirely on chance, given the overall dis-
tribution of nucleic acids in the DNA sequence un-
der consideration. As the probabilities of the occur-
rence of s are based on two population models, this
amounts to the likelihood ratio, as defined in statis-
tics. It is also (somewhat unrealistically) assumed
that character distributions at different positions are
independent. That way, for a string s = c
1
c
2
...c
L
,
of length L, the probability of its random occurrence
would be P
G
(s) =
∏
L
i=1
p
g
(c
i
), where p (c
i
) stands for
the probability of an individual character.
In order to estimate P
F
for a given string, one also
assumes the independence of probabilities for char-
acter occurrences at different positions. For any po-
sition i, we estimate the probability of occurrence of
any base p
f ,i
(b) based on how frequently it occurred
at the particular position i in known binding patterns.
Thus, having a string s = c
1
c
2
...c
L
, of length L, the
probability that it occurred under the distribution spe-
cific for the particular protein binding sites would
be P
F
(s) =
∏
L
i=1
p
f ,i
(c
i
). This approach can suffer
from artifacts (for instance, if only combinations “AG”
or “TC” would equally likely occur within motif in-
stances used to construct the matrix, once it is con-
structed it would assign equally high scores to com-
binations of “AC” and “TG” which have never been
observed), which has led to the development of di-
nucleotide (Gershenzon et al., 2005) and even more
elaborate models, and it can also be imprecise due
to incomplete experimental data or overly permissible
thresholds. However, over many years of its applica-
tion it has been shown to yield better results than raw
pattern matching, either exact or approximate. If it is
only a relatively small number of motifs used for the
construction of a PWM, it may be more appropriate to
construct a finite state automaton which would recog-
nize all these motifs (Aho and Corasick, 1975), rather
than approximating through a PWM, but that then in-
troduces the risk of over-fitting.
Expanded, the likelihood ratio P
F
(s)/P
G
(s) is then
∏
L
i=1
p
f ,i
(c
i
)/
∏
L
i=1
p
g
(c
i
) =
∏
L
i=1
[p
f ,i
(c
i
)/p
g
(c
i
)].
One can take a logarithm of this formula and con-
vert it to additive form
∑
L
i=1
log
2
[p
f ,i
(c
i
)/p
g
(c
i
)], al-
though some correction factors are needed in order
to avoid taking a logarithm of zero when a charac-
ter does not appear at a given position in any of the
motifs used to construct the matrix. The matrix as-
sociated with the protein binding pattern of length L
has L columns and 4 rows, one for each nucleotide
‘A’, ‘C’, ‘G’ or ‘T’. If a base b occurs m
b
times at the
position corresponding to matrix column i within M
known binding sites, then p
f ,i
(b) = m
b
/M, and if it
occurs n
b
times within N nucleotides in the genome,
then p
g
(b) = n
b
/N. The matrix entry for base b in
column i thus contains log
2
(m
b
N/n
b
M). An illustra-
tion of a set of motifs used to determine a PWM, and
the resulting matrix, is shown in Figure 1. In practice
there are several variants of PWMs, however they are
all based on the same principle.
Once a PWM is constructed, it can be used for
scanning genomic sequences, for motifs which are
sufficiently similar to these captured by the matrix.
Looking at a string s = c
1
c
2
...c
L
one locates the
corresponding row of the matrix for each c
i
, in col-
umn i, and adds these values to obtain the likelihood
ratio P
F
/P
G
. If that likelihood ratio is above the
pre–determined (and inevitably heuristic) threshold,
a match is declared. Since the shift for just one posi-
tion can result in entirely different score, PWM match-
ing programs advance for one position, and start the
matching process over the entire matrix every time
after the shift has been made. As matrices usually
do not feature too many columns, reflecting the fact
that they model short motifs, this does not lead to
intractability, yet it slows down any search for an
order of magnitude, and on the genomic scale that
presents a problem. Pruning techniques have been
explored, although one can only stop further match-
BIOINFORMATICS 2010 - International Conference on Bioinformatics
68
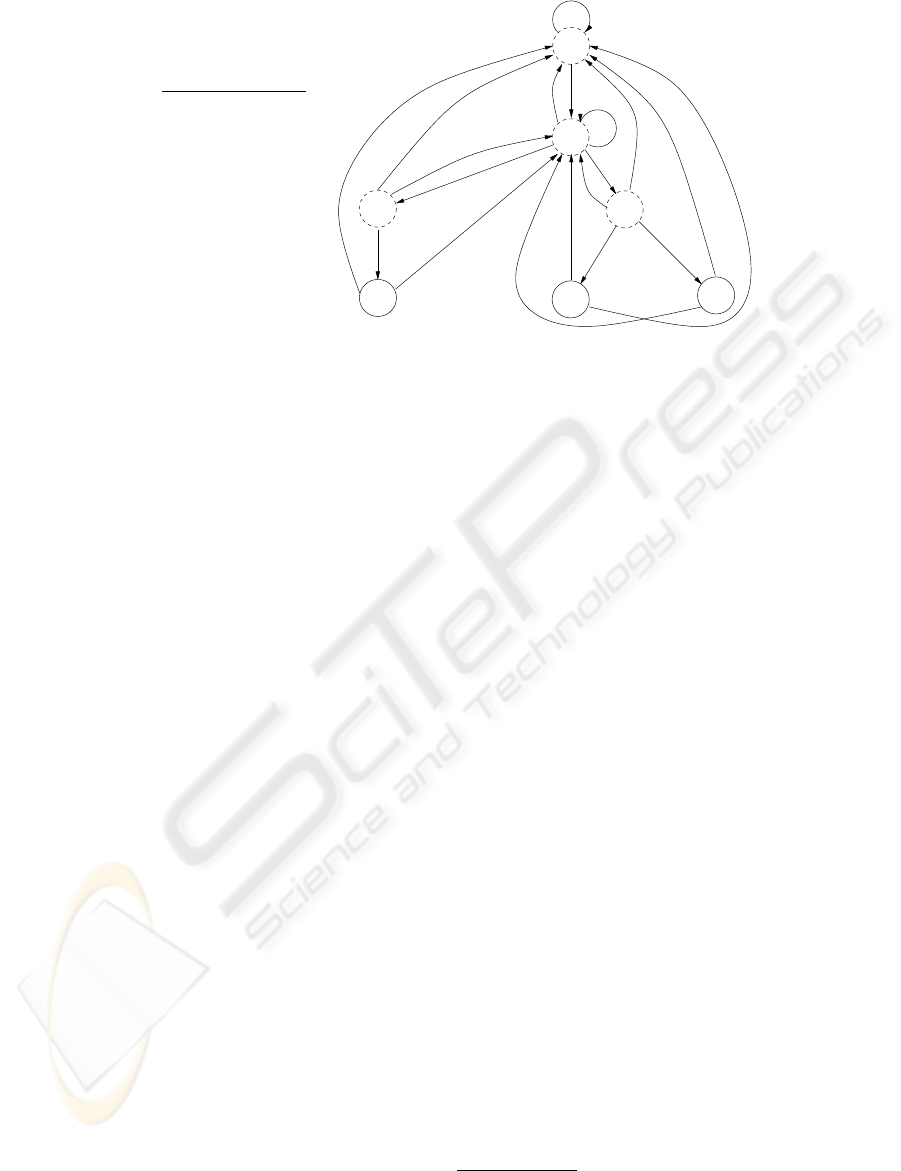
min
A −1 2 4
C 3 1 −9
G 0 −2 1
T −5 3 3
0
3
56
9
9
10
A,G,T
C
C
C
A
T
G
AA
C
G,T
T
C
G
C
A,G,T
A,G,T
A,G,T
C
a)
b)
c)
2 5 9
Figure 2: An example of an FSA created for a simple PWM: a) Position weight matrix; b) Minimal scores which have to be
reached at every position in order for threshold value of 9 to be met at the end (a match); c) FSA constructed based on the
matrix. Only three strings. “CAA”, “CTA” and “CTT”, would score sufficiently high to meet the threshold, as reflected by three
paths from the root to the reporting nodes (level 3), shown as solid circles. Scores at each node are shown inside the circles.
Transitions are guided by the letters labeling the edges.
ing attempts from a position if it has been determined
that the score–so–far is insufficient for a match. The
other option, recognizing a match before all charac-
ters have been examined is not possible, since some
letters at some positions may contribute (large) neg-
ative scores. Other algorithmic solutions have also
been applied, such as building indexing schemes to
facilitate matching of multiple matrices in the same
sequence (Liefooghe et al., 2006).
3 ALGORITHM
We here present an algorithm which matches a single
Position Weight Matrix against a genomic sequence
in linear time.
We start by pre-processing the matrix M , of di-
mension 4× L, into a tree–like structure, following the
basic ideas of classic algorithms of Knuth–Morris–
Pratt (Knuth et al., 1977) and Aho–Corasick (Aho and
Corasick, 1975). For every position p our algorithm
keeps track of its longest possible suffix k..p,1 < k <
p, in M , which can still result in a match, and thus
the amount of shift which can be made after M has
been successfully matched, or when it has been de-
termined that a match at the current starting position,
represented by the root, is not possible.
In order to enable the tracking, the matrix M is
thus converted into a finite state machine, implement-
ing a tree T with cross–linked branches. At every
node of the tree a structure is maintained, with the
following fields:
level: Keeps track of the length of the branch starting
at the root and ending at the current node. This
information is used to determine whether a match
along the current branch is still possible, and to
check whether a match has already been success-
ful (when a node whose level equals L is reached).
score: Keeps track of the score achieved so far along
the path from the root through the current node.
If the score is less than required for the current
level it is an indication that no match is possible
at the position currently aligned with the root and
a shift to a suffix has to be made; if a match has
been achieved, this score can be reported along
with match data.
suffix: A pointer to another node in T , positioned
on the branch which represents a suffix of the
branch ending in the current node (the longest suf-
fix which can still lead to a viable match from its
starting position). The target node of this pointer
follows the transition on the same letter as the cur-
rent node
1
.
move: A four–element array, providing a pointer to
another node in T , directing the move on each
of the four letters of the DNA alphabet (‘A’, ‘C’,
‘G’ and ‘T’). It can lead to forward motion if a
match along the current branch is still possible, or
backward to another path starting from the root
(a suffix) if the match at the currently examined
position cannot be achieved.
The preprocessing starts with the establishment of
a score array minimum, whose dimension L equals the
1
In our implementation we have kept this field outside of
the FSA, as it is used only once during the pre-processing of
a matrix, in situations when the branch needs to be changed
on an occurrence of a letter.
LINEAR--TIME MATCHING OF POSITION WEIGHT MATRICES
69

Algorithm 3.1: PREPROCESS(matrix,dimension,threshold)
// Find the minimal values necessary at positions
minimum[dimension] ← threshold
for i ← dimension − 1 downto 0
do
max ←Maximal value in matrix column i + 1
minimum[i] ← minimum[i +1] − max
//Process the root
root.level ← 0
root.score ← 0
root.su f f ix ← root
for letter ←A,C,G,T
do
score ← matrix[letter][1]
if score < minimum[1]
then root.move[letter] ← root
else
child.score ← score
child.level ← 1
child.su f fix ← root
root.move[letter] ← child
ENQUEUE(child)
// Process the remaining nodes, breadth–first
while Queue not empty
do
current ← DEQUEUE()
if current.level = dimension
then
for letter ←A,C,G,T
do current.move[letter] ← current.su f f ix.move[letter]
else
for letter ←A,C,G,T
do
score ← current.score + matrix[letter][current.level + 1]
if score < minimum[current.level + 1]
then current.move[letter] ← current.su f f ix.move[letter]
else
child.score ← score
child.level ← current.level + 1
child.su f fix ← current.su f f ix.move[letter]
current.move[letter] ← child
ENQUEUE(child)
return (root)
Algorithm 3.2: MATCH(matrix,text,threshold)
track ← PREPROCESS(matrix,matrix
column number,threshold)
for i ← 1 to text length − matrix column count + 1
do
track ← track.move[text[i]]
if track.level = matrix column count
then Report a match at i − matrix column count + 1, scoring track.score
Figure 3: Pseudo–code of the PWM matching algorithm.
length of the motif represented by M . Each entry in
minimum records the minimal score which must be
achieved at that position in order to lead to a possible
match. Since a match is defined as a sequence scoring
at threshold value or higher, it must be minimum[L] =
threshold. If max[i] is the maximal score recorded
in the i-th column of M , then minimum[i − 1] =
minimum[i] − max[i]. Whenever a position p in M is
reached it is checked whether the score so far is still
greater than or equal to minimum[p].
The FSA T is constructed in the breadth–first fash-
ion, after the root node has been formed, and its im-
mediate children have been placed in the queue (if
their score warranted the placement). Every time
a node is dequeued, it is first checked if its level l
equals L. If that is the case (indicating time to re-
port a match and move on), its transitions on all four
letters are determined by following the transition on
that letter from the (suffix) node pointed to by the
su f f ix pointer. If l < L, forward transitions (and the
increment of the level) are considered. If the score of
the transition on a letter falls below the minimum re-
quired at l, a back pointer is created to the extension
from the node pointed to by the su f f ix. Otherwise,
BIOINFORMATICS 2010 - International Conference on Bioinformatics
70

a child node is created and enqueued, defining a for-
ward transition on the letter. An example of an FSA
created for a simple PWM is provided in Figure 2,
and the pseudo–code of the preprocessing algorithm
is provided in the function Preprocess in Figure 3.
The complete matching function is shown as function
Match.
After the preprocessing is completed, the matrix
matching itself is rather straightforward. The algo-
rithm maintains two pointers, one to the currently ex-
amined position i in the DNA sequence (initialized at
1), and the other to the current node in T (initial-
ized at the root). A transition in T is done depending
on the character at position i, and if the level of the
reached node equals L a match can be reported (with
appropriate score). This process continues until the
end of the sequence is reached.
4 ALGORITHM PERFORMANCE
Since the matching done by this algorithm is com-
pletely guided by the FSA T , it can be proven cor-
rect by observing that every matching substring would
lead to a traversal of a path from the root to a node
at level L, and that no mismatching substring would
reach level L. Since every time an insufficient score
is obtained it would result in a decrease in the current
level, and every time a sufficient score is obtained it
results in an increase of the current level, the above
properties will hold if it can be proven that the back
pointers indeed lead to a node N such that the path
from the root to N represents the longest feasible suf-
fix of the currently examined substring (i.e. path from
the root).
The formal proof can be derived by mathematical
induction, showing that the following invariants hold
every time a node is dequeued and processed, during
the matrix pre-processing phase:
1. If there is a viable continuation from the position
represented by the node, on a particular letter, that
leads to the creation of a forward link, i.e. a node
at the next deeper level.
2. If there is no continuation from the position rep-
resented by the node, for each letter, that leads to
the creation of a backward link, to a node at the
same level as current, or closer to the root.
3. The su f f ix pointer of a newly enqueued node
points to another node in the FSA, at some level
closer to the root, which is the end of a path
from the root representing the longest suffix of
the string represented by the path to the enqueued
node, and which can still yield a match.
4. If a path cannot be continued to a further level,
on some letter, then the transition on that letter is
made to a node representing the end of the longest
suffix of the current path which can still yield a
match.
For the induction base, it is trivial to show that
properties 1 through 4 hold at the time the root is
processed (initialization), and its children are being
placed in the queue. We can assume that they are also
satisfied when k
th
node is being processed, and show
that they hold after the k + 1
th
has been handled. It
should be noted that the su f f ix pointers are already
fixed at the time of enqueuing the node.
Invariant 1 holds trivially, as it is the decision
made in the code while processing the dequeued node.
Since the tree is processed breath–first, that means
that all nodes at depths smaller than that of the cur-
rent one have already been processed. If there is no
viable continuation of a match on a currently consid-
ered letter, that leads to following the transition from
the node pointed to by the su f f ix pointer, which is,
by invariant 3, at a level closer to the root, and thus,
by invariants 1 and 2 being already satisfied at earlier
nodes, cannot lead to level deeper than the current.
This proves that invariant 2 also holds after the cur-
rent node is processed.
If there is a viable continuation from the current
node on any particular letter, then the su f f ix pointer
assigned to the newly created child is to the link of
the node at the other end of the current su f f ix pointer,
and thus at the level closer to the root than the newly
created child. If the node pointed to by the current
su f f ix featured a viable forward move on the letter,
that extends that suffix which can yield a match. If
not, it extends its longest suffix which can, by the in-
duction hypothesis, and thus represents a new longest
suffix which can still yield a match. Therefore, invari-
ant 3 also holds.
When a forward move (one continuing the match)
cannot be done on a particular letter, it is being done
from the node pointed to by the su f f ix pointer, which,
by invariant 3, represents the longest suffix of the cur-
rent path which can still yield a match. Therefore,
the transition is being made to the node extending the
other end of the su f f ix pointer on that letter, and the
invariant 4 holds.
During the search phase the traversal of the FSA
T proceeds in the forward direction (i.e. to deeper
levels) for as long as a match is still possible (invari-
ant 1). When it is no longer the case, invariant 4 guar-
antees that the jump is being made to the next position
from which there may be a possible match. As a deter-
mined mismatch cannot lead to a forward move in T
LINEAR--TIME MATCHING OF POSITION WEIGHT MATRICES
71

no mismatching positions can lead to reaching level L
(and thus be reported), and as the jump is being made
to the beginning of the longest suffix of the currently
examined substring which can still yield a match (in-
variant 4), no matching positions can be skipped. We
thus conclude that the algorithm is correct.
4.1 Space Performance
This algorithm can have large space requirements.
For a matrix of length L it can theoretically build an
FSA with O(4
L
) nodes, since every possible match-
ing substring has to be represented by a path through
T reaching level L. However, all internal nodes, and
thus their children as well, for which it has been es-
tablished that they could not lead to a match, are
promptly pruned. Since in practice PWMs are con-
structed, and their thresholds set, so that they accept
a very limited number of variants of the target site,
it is expected that in most practical situations prun-
ing will be quite dramatic. The only situation when
there can exist a large conglomeration of nodes to-
wards the top of the tree, the most space–consuming
setting, is when there is a variety of possible char-
acters occurring in relatively high percentages at the
left hand side of the pattern, thus dictating extensive
branching near the root of the tree, and a more inclu-
sive threshold value. However, this situation practi-
cally never happens, since tails exhibiting substantial
variations normally do not get included in the patterns
captured by PWMs. Towards the bottom of the tree the
only branches which have not been pruned would be
these leading to a pattern variant matching the matrix
(as set by the given threshold).
Apart from the FSA encoding the matrix, the only
space requirement for the matching process itself is
the space needed to store the sequence in which the
matching is to be done.
4.2 Time Performance
Since, during the matching, no character in the text is
examined more than once (as signified by the single
for–loop with constant–time body in the algorithm in
Figure 3), this process clearly executes in linear time.
The construction of the FSA (pre-processing) takes
time proportional to the number of nodes which are
being created (as each node is being processed in con-
stant time), which, under the worst–case scenario of a
large number of matching strings, can be exponential.
However, since the children of the pruned nodes never
get processed, the exponential blowout is expected
to take place only at shallow depth, towards the top
of the tree. Furthermore, whereas pre-processing of
the long PWMs would take the longest time, these are
precisely the cases where the gain from subsequent
linear–time matching would be the largest.
Even as the PWMs are generally short (rarely ex-
ceeding 15 columns, and almost never exceeding 25)
and pruning extensive (as the thresholds are usually
very stringent), the pre-processing step has the po-
tential of annihilating the gains from the subsequent
linear–time processing. This algorithm is thus recom-
mended for use only in very large scale analyses, such
as our whole–genome scans (Singh and Stojanovic,
2009). In our recent tests, done on a genomic seg-
ment of about 500 million bases (corresponding to a
large chromosome), the naive match was taking an
average of 144.33 seconds per matrix, on an Apple
Mac Pro 2.5 GHz Intel Core Duo with 4 Gb 667 MHz
DDR2 SDRAM memory laptop computer, while an im-
plementation of our algorithm was taking an average
of 16.58 seconds per matrix. On whole–genome scale
the average gain would be about 10–20 fold per ma-
trix.
5 DISCUSSION
The space requirements of this algorithm can be
further reduced by a simple extension of the pre-
processing step, alas at the price of an increase in the
computational time. This would require the mainte-
nance of two additional fields at the nodes of the FSA:
parent pointer and number of forward links. An ad-
ditional traversal pass through the FSA can then elim-
inate all partial paths which do not extend until the
bottom (match), reducing the number of nodes to less
than the sum of the lengths of all strings which would
score above the threshold. However, we have not
implemented this modification, as the space require-
ments of the FSA have never been a limiting factor,
and time was critical.
Often a PWM will feature letters which must not
be found at a specific position, with the correspond-
ing score in the PWM of (theoretically) −∞. This sit-
uation is particularly favorable to our algorithm, as
it leads to immediate pruning, especially when these
positions are concentrated towards the beginning of
the matrix. If they are concentrated towards the end,
the least favorable setting, one can do the matching
in the inverse complement of the sequence. For long
matrices one can also attempt the match of their most
specific core, then attempt the full match, using the
naive approach, only around the positions where the
core has matched.
Despite of its relatively expensive pre-processing,
we have found this algorithm very useful for whole–
BIOINFORMATICS 2010 - International Conference on Bioinformatics
72

genome scans, such as our search for the conglomer-
ations of variable motifs, with a potential of reducing
days of computation to just a few hours. This can
be of particular importance for the tools implemented
as a part of a web server. Our earlier version of the
matcher (Singh and Stojanovic, 2009) implemented at
http://bioinformatics.uta.edu/toolkit/motifs/ used di-
rect pattern matching (i.e. not based on PWMs), and
the development of this algorithm has allowed us to
consider the matrix–based approach, too.
ACKNOWLEDGEMENTS
The author is grateful to Abanish Singh, whose ef-
fort on motif finding and the implementation of the
whole–genome motif search has made us aware of the
need for this algorithm. This work has been partially
supported by NIH grant 5R03LM009033-02.
REFERENCES
Aho, A. and Corasick, M. (1975). Efficient string matching:
an aid to bibliographic search. Comm. Assoc. Com-
put. Mach., 18:333–340.
Apostolico, A., Bock, M., Lonardi, S., and Xu, X. (2000).
Efficient detection of unusual words. J. Comput. Biol.,
7:71–94.
Bryne, J., Valen, E., Tang, M., Marstrand, T., Winther, O.,
da Piedade, I., Krogh, A., Lenhard, B., and Sandelin,
A. (2008). JASPAR, the open access database of
transcription factor–binding profiles: new content
and tools in the 2008 update. Nucleic Acids Res.,
36:D102–D106.
Gershenzon, N. I., Stormo, G. D., and Ioshikhes, I. P.
(2005). Computational technique for improvement
of the position–weight matrices for the DNA/protein
binding sites. Nucleic Acids Res., 33:2290–2301.
Hannenhalli, S. and Wang, L.-S. (2005). Enhanced position
weight matrices using mixture models. Bioinformat-
ics, 21:i204–i212.
Hughes, J., Estep, P., Tavazoie, S., and Church, G. (2000).
Computational identification of cis–regulatory ele-
ments associated with groups of functionally related
genes in Saccharomyces cerevisiae. J. Mol. Biol.,
296:1205–1214.
Kel, A. E., G
¨
ossling, E., Reuter, I., Cheremushkin, E., Kel-
Margoulis, O. V., and Wingender, E. (2003). Match:
A tool for searching transcription factor binding sites
in dna sequences. Nucleic Acids Res., 31(13):3576–
3579.
Khambata-Ford, S., Liu, Y., Gleason, C., Dickson, M., Alt-
man, R., Batzoglou, S., and Myers, R. (2003). Iden-
tification of promoter regions in the human genome
by using a retroviral plasmid library–based functional
reporter gene assay. Genome Res., 13:1765–1774.
Knuth, D., Morris, J., and Pratt, V. (1977). Fast pattern
matching in strings. SIAM J. Computing, 6:323–350.
Liefooghe, A., Touzet, H., and Varr, J.-S. (2006). Large
Scale Matching for Position Weight Matrices. In Pro-
ceedings of the 7
th
Annual Symposium on Combina-
torial Pattern Matching, CPM 2006, volume 4009 of
LNCS, pages 401–412. Springer–Verlag.
Nelson, C., Hersh, B., and Carroll, S. B. (2004). The reg-
ulatory content of intergenic DNA shapes genome ar-
chitecture. Genome Biol., 5:R25.
Qin, Z., McCue, L., Thompson, W., Mayerhofer, L.,
Lawrence, C., and Liu, J. (2003). Identification of co-
regulated genes through Bayesian clustering of pre-
dicted regulatory binding sites. Nature Biotechnology,
21:435–439.
Singh, A. and Stojanovic, N. (2006). An efficient algorithm
for the identification of repetitive variable motifs in
the regulatory sequences of co–expressed genes. In
Proceedings of the 21
st
International Symposium on
Computer and Information Sciences, volume 4263 of
LNCS, pages 182–191. Springer–Verlag.
Singh, A. and Stojanovic, N. (2009). Genome–wide search
for putative transcriptional modules in eukaryotic se-
quences. In Proceedings of BIOCOMP’09, pages
848–854.
Stojanovic, N. (2009). A study on the distribution of phylo-
genetically conserved blocks within clusters of mam-
malian homeobox genes. Genetics and Molecular Bi-
ology, 32:666–673.
Stormo, G. (1990). Consensus patterns in DNA. Methods
Enzym., 183:211–221.
The ENCODE Project Consortium (2007). The ENCODE
pilot project: Identification and analysis of func-
tional elements in 1% of the human genome. Nature,
447:799–816.
van Helden, J. (2004). Metrics for comparing regulatory se-
quences on the basis of pattern counts. Bioinformatics,
20:399–406.
Wingender, E. (2008). The TRANSFAC project as an exam-
ple of framework technology that supports the analy-
sis of genomic regulation. Briefings in Bioinformatics,
9:326–332.
Young, J. E., Vogt, T., Gross, K. W., and Khani, S. C.
(2003). A short, highly active photoreceptor–specific
enhancer/promoter region upstream of the human
rhodopsin kinase gene. Investigative Ophtamology
and Visual Science, 44:4076–4085.
LINEAR--TIME MATCHING OF POSITION WEIGHT MATRICES
73
