MODELLING GLYCAEMIA IN ICU PATIENTS

A Dynamic Bayesian Network Approach

Catherine G. Enright

, Michael G. Madden

, Stuart Russell

, Norm Aleks

, Geoffrey Manley

John Laffey

, Brian Harte

, Anne Mulvey

and Niall Madden

National University of Ireland, Galway, Ireland

University of California, Berkeley, U.S.A.

University of California, San Francisco, U.S.A.

University Hospital Galway, Ireland

Keywords: Dynamic Bayesian Network, Glycaemia.

Abstract: Presented in this paper is a Dynamic Bayesian Network (DBN) approach to predict glycaemia levels in

intensive care patients. The occurrence of hyperglycaemia is associated with increased

morbidity and

mortality in critically ill patients. Due to the large inter-patient and intra-patient variability, the sparse nature

of observations, inaccuracies in the data and the large number of factors that influence glycaemia, the

system being modelled contains several sources of uncertainty. In the context of this uncertainty, the DBN-

based system presented here performs extremely well. By using a DBN we integrate multiple strands of

temporal evidence, arriving at varying time intervals, to determine the most probable underlying

explanations. A key contribution of this work is that it presents a principled technique for recalibration of

model parameters from general population-level values to patient-specific values, based entirely on standard

real-time measurements from the patient. While in this paper we apply our approach to the glycaemia

problem, this approach is equally applicable to other applications where unseen variables must be assessed

and individualized in real time.

1 INTRODUCTION

Proper control of glycaemia (i.e., serum glucose

levels) in critically ill patients in the intensive care

unit (ICU) is a subject that is of great importance to

physicians. Tight control of serum glucose levels has

previously been demonstrated to improve outcome

in a predominantly surgical population of critically

ill patients (Van den Berghe et al. 2001). In contrast,

the recent NICE-SUGAR study found that

attempting to keep serum glucose levels within a

tight range actually increases mortality rates (The

NICE-SUGAR Study Investigators 2009).

Therefore, the optimal target range for blood glucose

and the optimal approach to controlling blood

glucose levels in critically ill patients is still unclear.

The goal of this work is to develop a system that

accurately predicts the glycaemia levels of a patient

receiving insulin and glucose infusions. This would

provide physicians with more accurate real-time

estimates of glycaemia levels, which in turn would

be useful in determining the optimal dosage for a

given patient, through modelling the most likely

effects of planned dosages.

To achieve this goal, we develop a Dynamic

Bayesian Network (DBN) model that is derived

from an existing differential equation model of

glycaemia in ICU patients (see Section 2.1). By

recasting it as a DBN, we provide a framework for

computing solutions with continuous re-estimation

of parameters, taking account of dependencies

between variables and conditional distributions on

them. In this way, it interprets the system as being a

set of stochastic differential equations (SDEs).

Unlike the original system of differential equations,

in the DBN model all of the model terms are

allowed to vary, and accordingly are automatically

recalibrated to patient-specific values over time.

At a more general level, this paper introduces a

method for mapping a system of differential

452

G. Enright C., G. Madden M., Russell S., Aleks N., Manley G., Laffey J., Harte B., Mulvey A. and Madden N. (2010).

MODELLING GLYCAEMIA IN ICU PATIENTS - A Dynamic Bayesian Network Approach.

In Proceedings of the Third International Conference on Bio-inspired Systems and Signal Processing, pages 452-459

DOI: 10.5220/0002750804520459

 SciTePress

equations directly to a DBN, so that they can be

solved in a way that allows all model terms to vary,

while directly incorporating both continuous and

sporadic temporal evidence in the solutions.

1.1 Hyperglycaemia in an ICU Patient

Hyperglycaemia in non-diabetic patients is a

common phenomenon in an ICU setting (Van den

Berghe et al. 2001). The standard practice is to

control a patient’s glucose levels using glucose and

insulin infusions. Each patient reacts differently to

these insulin infusions depending on the nature of

their illness, their insulin sensitivity and other

medication they may be receiving. As well as inter-

patient variability, there is intra-patient variability. A

patient’s condition and medication intake vary

considerably while in the ICU, and hence so does

the response to insulin.

To assess a patient’s response to insulin, glucose

levels are typically measured at intervals of between

one and four hours in an ICU ward. When one

considers that the half-life of insulin is only a few

minutes, a lot can happen in a four hour interval.

However, this is the only quantitative evidence

available to physicians. From this sparse data, a

physician must prescribe an appropriate dosage

regime.

Another consideration is the quality of the data.

There may be inaccuracies in the recorded dosage

quantities and the time stamps on these records.

Plasma glucose measurements are not always

precise: depending on the method used error levels

vary from 3% -12% (Chase et al. 2006).

1.2 Why use a DBN?

The challenge when building a model to predict an

ICU patient’s insulin/glucose dynamics reflects the

challenge facing a physician trying to keep a

patient’s glucose levels within safe limits. Given the

large inter-patient and intra-patient variability, the

large number of factors that influence glucose levels

and very sparse evidence, creating an accurate

model is difficult.

Our objective in this work is to build a model

capable of reasoning in the context of this

uncertainty. However, as well as dealing with

uncertainty, the temporal nature of the problem must

also be addressed. A patient’s glucose level depends

not only on the current I.V. (intravenous) infusion

rates but also past infusion rates and past glucose

levels. Dynamic Bayesian Networks are an effective

tool for modelling uncertainty in real time in a time-

varying environment as was shown by Aleks et al.

(2008). That paper describes an early application of

full DBNs to analysing ICU data, and demonstrated

very accurate detection and removal of artefacts in

the arterial-line blood pressure sensor data.

Other DBN applications in the medical setting

have used only discrete variables. The applications

include a network to diagnose ventilator-associated

pneumonia in ICU Patients (Charitos et al. 2009)

and a prognostic model for carcinoid patients (van

Gerven et al. 2008). In the separate, but related

topic, of simulating human physiology, Abkai &

Hesser (2009) recognised the need to use

deterministic and probabilistic models. However

unlike our approach, they separate ordinary

differential equation solvers and DBN models.

It is assumed that readers are already familiar

with Dynamic Bayesian Networks. They are

described in a number of Artificial Intelligence

textbooks, for example Russell & Norvig (2002).

2 A GLYCAEMIA MODEL

2.1 A Basic Mathematical Model of the

Glucose/Insulin Dynamics

The first step in building the DBN model is to

establish a relationship between the administered

glucose and insulin and the resulting plasma levels.

The ICU-Minimal Model (ICU-MM) developed by

Van Herpe et al. (2007) is a mathematical model of

this relationship. It is an adaptation of Bergman’s

Minimal Model (Bergman et al. 1981) specifically

for ICU patients. The ICU-MM is described by a

system of four differential equations:

dG(t)/dt= (P

− X(t))G(t) − P

(1a)

dX(t)/dt=P

X(t) + P

(t) − I

)

(1b)

(t)/dt= α max(0,I

(t))

− n(I

(t)−I

)+F

(1c)

(t)/dt= βγ(G(t)

−h)

−

(t)

(1d)

The terms are briefly explained in Appendix 1.

However, for a detailed explanation of the model,

please refer to Van Herpe et al. (2007).

Other models exist for describing the

glucose/insulin interaction in critically ill patients.

Chase et al. (2006) reviewed three different

metabolic models used in critical care glycaemia

control. Since then, other models have been

proposed (Lin et al. 2008) (Hovorka et al. 2008).

MODELLING GLYCAEMIA IN ICU PATIENTS - A Dynamic Bayesian Network Approach

453

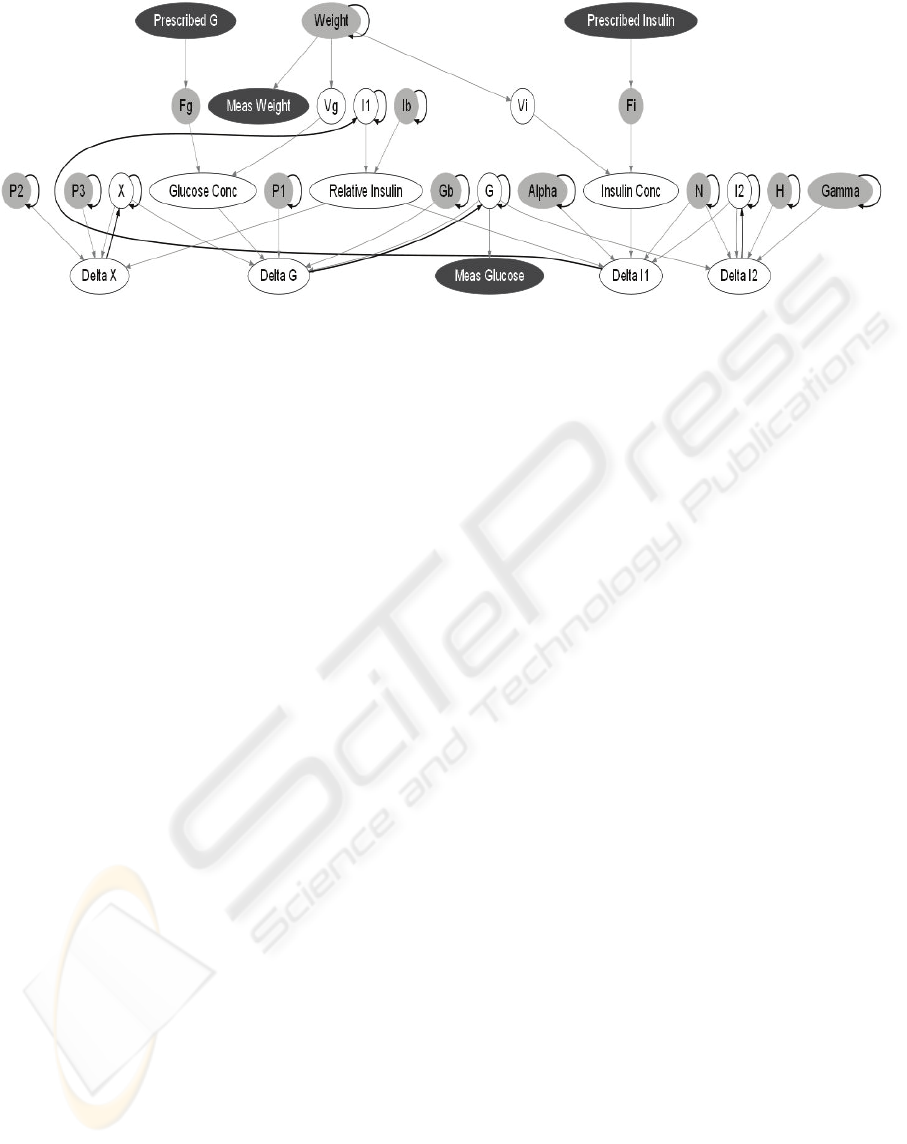
Figure 1: A Dynamic Bayesian Network for Glycaemia in ICU Patients. Grey nodes are conditionally Gaussian and vary

over time. White nodes are deterministic and black nodes are observed. Grey arrows connect nodes within a time slice;

black arrows connect nodes between time slices.

Both these models are of interest. The ICU-MM

however is based on Bergman’s Minimal Model.

Bergman’s model is the most well-known and well-

understood model that exists of glucose metabolism.

Indeed, Bergman’s Minimal Model has previously

been re-worked into a Bayesian graphical model

(Anderson and Højbjerre 2003). Their approach is,

however, significantly different to ours. They first

derive a system of SDEs from the Minimal Model

and then specify the SDEs as a DBN. As will be

explained in Section 2.2, our approach does not

require such transformation of a system of

differential equations prior to constructing the DBN.

It should also be noted that the Minimal Model is

less complex than the ICU-MM. It was developed to

assist in the diagnoses of diabetes and not for use in

the ICU setting.

2.2 The DBN Model

A DBN is made up of a series of discrete time slices.

In our model we use a one-minute time interval.

Figure 1 shows one time slice of the DBN

constructed based on the ICU-MM. Grey arrows

connect nodes within a time slice; black arrows

connect nodes from the previous time slice to the

current time slice.

The DBN contains both observed and hidden

variables. Given the history of observations up to the

current time, the DBN can compute a probability

distribution over the values of any or all of the

hidden variables: past, present, or future. Observed

nodes are coloured black in Figure 1. In our case, the

prescribed insulin and glucose infusion rates and the

measured weight of the patient are observed, and can

be viewed as inputs to the DBN. The intermittent

plasma glucose level measurements are also

observed. These glucose observations ground the

DBN in reality, so that the inferred values for the

hidden variables are specific to the patient and take

into account all of the measurements made. We are

specifically interested in inferring current and future

glucose levels, even when the most recent

measurement may have been several hours in the

past. By setting the values of nodes that correspond

to hypothetical future actions and asking the DBN to

predict future glucose levels for the patient, we can

also evaluate and select among possible treatments.

The quantitative aspect of the DBN model

consists of a conditional distribution for each node

conditioned on its parents’ values. In this system, a

node is either deterministic (i.e. its value can be

determined exactly from its parent values) or

Gaussian (i.e. the conditional distribution is a

Gaussian whose mean is a linear function of its

parents’ values). Gaussian nodes are shaded grey in

Figure 1; deterministic nodes are clear with a black

outline.

The observed value for plasma glucose (Meas.

Glucose in the DBN) is assumed to contain a certain

amount of measurement error. It is therefore

modelled with a Gaussian distribution whose mean

is its parent node, the true plasma glucose level, G.

Likewise, the data from the ICU reflects the

prescribed I.V. infusion rates for insulin and

glucose; the actual administered rates may be

different. Therefore we model the actual rates with

Gaussian distributions whose means are the

prescribed rates.

In many cases truncated Gaussian distributions

are used, in order to constrain the DBN to postulate

values that are not unrealistic for nodes. For

example, the true I.V. infusion rate for insulin (F

)

cannot be a negative value, only positive values are

BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing

454

possible. The mean, standard deviation values and

limits used for the Gaussian nodes are detailed in

Appendix 2.

Similar limits were also placed on some

deterministic nodes. For example, it is not possible

to have a negative quantity of glucose in plasma, so

a limit is placed on node G to reflect this.

In the DBN, all terms of the ICU-MM can vary

over time as a patient’s insulin sensitivity changes.

Even terms that are fixed parameters in the original

ICU-MM model are allowed to vary in the DBN.

The delta nodes capture changes in quantities

over time. These changes are calculated using the

differential equations of the ICU-MM. Each delta

node has, as parent nodes, the various terms needed

to solve the appropriate differential equation.

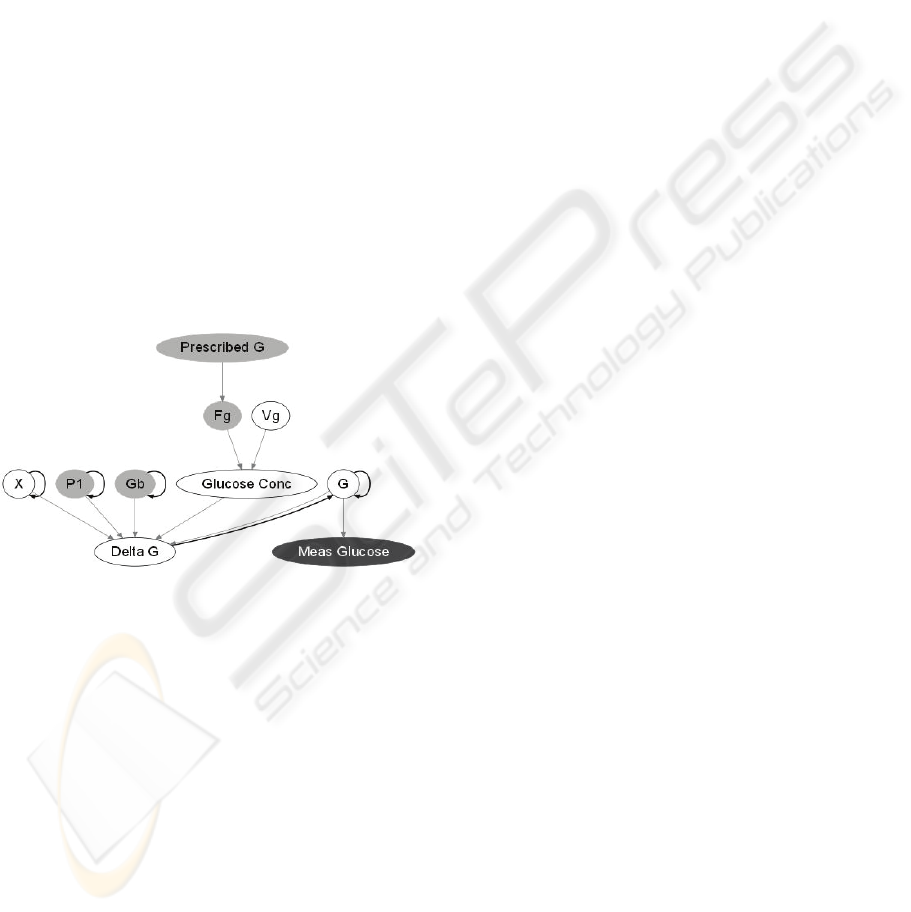
To illustrate this, Figure 2 shows a section of the

DBN that is related to Eq. (1a) of the ICU-MM.

Here, the Delta G node determines the per-minute

change in plasma glucose levels. The current plasma

glucose level is determined based on the glucose

level and Delta G calculated in the previous time

slice. Each of the terms in the differential equation

for G is represented as a parent node of Delta G.

Figure 2: Section of DBN for predicting plasma glucose

levels.

We used in-house software for building the DBN

and for performing inference using particle filtering.

Particle filtering is the means by which we

determine the most probable states of the DBN

nodes. We performed preliminary sensitivity

analyses to determine that, for this DBN, using

50,000 particles gave an acceptable balance between

execution time and accuracy.

2.3 Data Selection

In testing our model, we used data from real patients

in the ICU of University Hospital Galway.

Permission for extracting this data was given by the

Galway Research Ethics Committee, UHG. All

records were anonymised and stored on encrypted

drives.

For this research, data from patients with the

following characteristics was selected:

• Sepsis as a primary diagnosis

• Non-diabetic

• Not receiving steroids

• No major organ failure

In the next section, the results for one sample

patient are presented.

2.4 DBN Glycaemia Prediction for a

Sample Patient

Patient 23 was an ICU patient with acute pancreatitis

who was administered N6 OliClinomel 900 E

(glucose) and Actrapid (human soluble insulin)

intravenously. As was explained in Section 2.2, the

actual infusion rates are modelled as Gaussian

distributions whose means are the prescribed

infusion rates. The standard deviations on the nodes

for the actual infusion rates, F

and F

, represent the

expected error in the records. It was assumed that

the records for the prescribed infusion rates were

reasonably accurate therefore the standard deviations

on the nodes F

and F

were set to relatively small

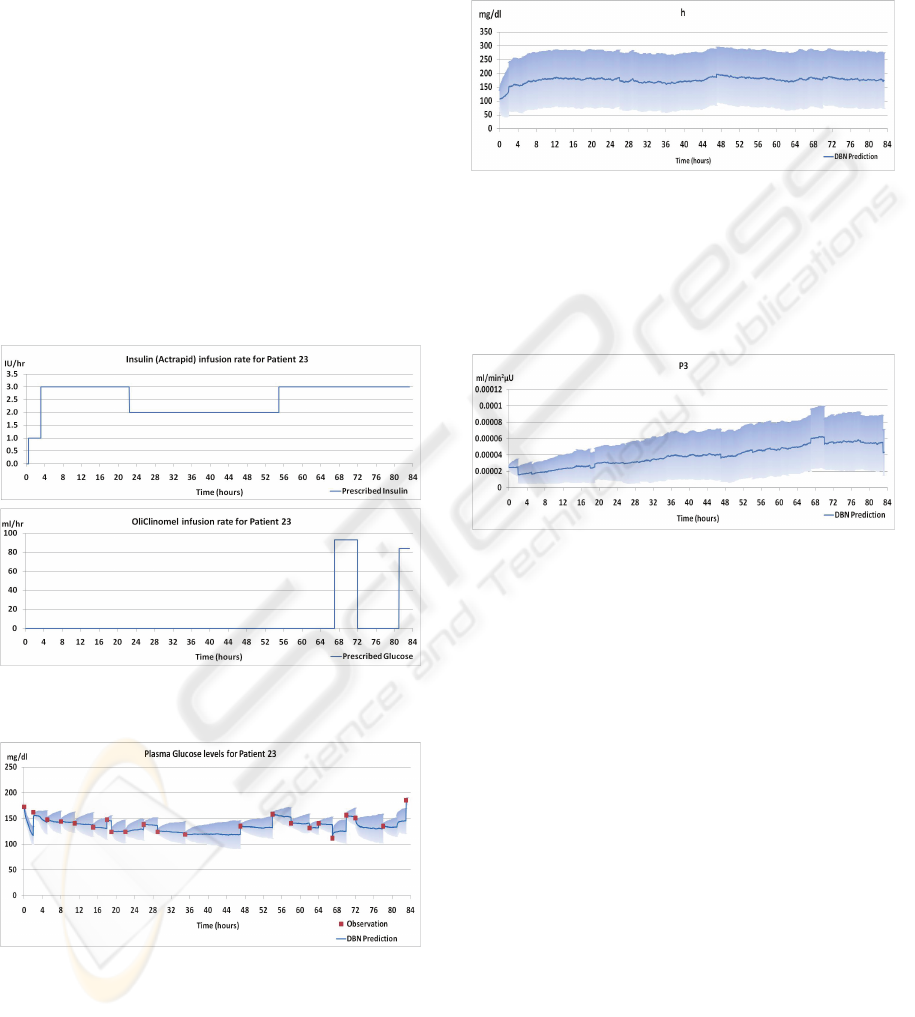
values. The prescribed infusion rates are shown in

Figure 3.

In the ICU, plasma glucose levels are measured

at frequencies of between one and four hours. The

square markers (coloured red) in Figure 4 show

these measured glucose levels. These values are

used as observations by the DBN to ground it in

reality.

As can be seen in Figure 4, the observations for

plasma glucose are intermittent; the DBN therefore

makes internal predictions of plasma glucose levels

in between observations. The accuracy of the

predictions can be evaluated by comparing the

predicted value at the time of a measurement to the

actual value. In Figure 4, the dark blue lines are the

mean values inferred by the DBN at each minute,

and the lighter blue shaded areas show the standard

deviations of inferred values, thereby giving a sense

of the uncertainty associated with its predictions

over time.

One can observe that the mean value often jumps

when a new observation becomes available. There

are factors which are unknown to the model that

influence plasma glucose levels. Because of these

unknown factors, the mean values predicted by the

model can drift from reality in between

observations. Once a new observation is available,

the model realigns itself with reality. Although the

MODELLING GLYCAEMIA IN ICU PATIENTS - A Dynamic Bayesian Network Approach

455

figures do not show it, the DBN can compute the

distribution over past glucose levels given all

previous and subsequent measurements; this

“smoothed” estimate does not have jumps in the

estimated value.

It is informative to consider the way that the

standard deviations vary over time. Because the

DBN always assumes some variability of values

over time, and because actual observations of

plasma glucose levels are available very

intermittently (once every few hours), as the time

from the last observation increases, so too does the

range of possible values. Therefore the uncertainty

of the predictions also increases. As uncertainty

increases, the mean values also drift. This is why the

standard deviations on the inferred plasma glucose

grow between observations. Whenever an

observation is provided, its plasma glucose

prediction realigns to the actual level, and its

uncertainty collapses.

Figure 3: The prescribed infusion rates used as inputs to

the DBN.

Figure 4: Glucose Levels inferred from the DBN.

It is interesting to observe the model terms to see

how they vary over time. Take for example, the

values inferred for h shown in Figure 5. Here, h

represents the glucose threshold. When this

threshold is reached, the body produces endogenous

insulin. The model starts with a population average

but quickly adjusts to a patient-specific value within

the first 4 hours. Once the node adjusts to the

patient-specific value, h does not vary to such a

large degree.

Figure 5: Values for h inferred by the DBN.

In contrast with this, other terms vary considerably

over time. P

for example, shown in Figure 6,

continues to rise over time. This variation reflects

the changing condition of the patient and the

possible effect of other medical interventions.

Figure 6: Values for P3 inferred by the DBN.

3 DISCUSSION

One of the difficulties with the mathematical model,

on which the DBN is based, is that not only do the

model terms vary quite considerably between

patients, there is also a large intra-patient variability

over time. In Figure 7 we compare the results for the

DBN with those obtained by using just the

differential equation model (1a)-(1d). For the latter,

shown in the lower dashed line (coloured green),

computed solutions were obtained by using the

standard Euler's method (e.g., Iserles 2009). The

DBN and the differential equation solutions both use

the same initial values. Both use the I.V. infusion

rates for glucose and insulin as inputs. Only the

DBN considers the actual measured plasma glucose

values. As can be seen, the solution to the

differential equations on their own does not succeed

in tracking the plasma glucose levels over time,

since it does not include a mechanism to recalibrate

to the measured values. By contrast the DBN

performs reasonably well, because the DBN

BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing

456

considers real-time observations of the true state and

because the DBN allows the model terms adjust to

patient-specific values in each time step, so that its

predictions are much closer to the true state than

those of the simple mathematical model.

Figure 7: ICU-MM prediction using Euler's method vs.

DBN prediction.

It should be noted that in the original

implementation of the ICU-MM by Van Herpe et al.

(2007), they did not simply use fixed values as was

done for the solution of the differential equations in

Figure 7. Their strategy for dealing with the large

inter-patient and intra-patient variability was to

choose patient-specific terms to fit the data offline,

after analysing 24 hours of data for each patient, and

then re-estimating these parameters every hour or

every 4 hours.

Our DBN-based system uses quite a different

approach for recalibration of model parameters from

general values to patient-specific values. We select

Gaussian distributions, suited to the cohort of

patients in our dataset, as starting values for the

model, and the DBN then adjusts these terms in each

time-slice to find the best fit for the specific patient,

given all the evidence up to that point. Often the

first 24 hours in the ICU are the most critical and

also the most unstable. Having a model that is

calibrated to the patient in the first 24 hours is of

clinical value.

Despite the large variance of the initial parameter

estimates, the sparsity of the evidence, the

prevalence of uncertainty in the model, and the

omission of several factors from the model, the DBN

performs remarkably well. For example, the

predicted values for the hidden Plasma Insulin

variable, shown in Figure 8, are strongly correlated

with the prescribed insulin infusion rates as one

would expect.

Figure 8: Plasma insulin levels inferred by the DBN are

strongly correlated with the prescribed insulin infusion

rates.

The underlying mathematical model is relatively

simple. It does not fully describe the complexity of

the system being modelled. The only inputs to the

DBN model are the I.V. infusion rates and the

patient’s weight. Plasma glucose levels are the only

sources of evidence available to help align the DBN

to reality. This evidence is both sparse and

intermittent. The dynamics of the system being

modelled are constantly changing as the patient’s

insulin sensitivity changes. But by allowing the

model terms to vary, the DBN can anticipate these

changes, even though they are unobserved. The light

blue shaded areas in Figure 4 show the range of

possible values for plasma glucose predicted by the

DBN. New observations are generally within this

range.

4 FUTURE DIRECTIONS AND

CONCLUSIONS

4.1 Future Directions

The DBN model presented in this paper is a

relatively basic model. There are many factors that

influence how a patient reacts to insulin and glucose

infusions. These include the reason for which the

patient was admitted to the ICU. For example, a

patient with sepsis is more likely to have

hyperglycaemia than a patient who was admitted

following cardiac surgery (Chase et al. 2006). Then

there are interactions with other medications. For

example, steroids can reduce a patient’s insulin

sensitivity. Future models will incorporate these

important factors that influence a patient’s response

to insulin.

The current model assumes that all glucose is

administered intravenously. Many ICU patients are

fed enterally. Gut absorption of glucose must be

included if this model is to be of use in a clinical

setting.

MODELLING GLYCAEMIA IN ICU PATIENTS - A Dynamic Bayesian Network Approach

457

With these factors in mind we hope to work on

new systems of differential equations to model the

physical phenomena and also novel techniques to

solve these numerically. This work will enable a

comprehensive comparison of this DBN approach to

numerical simulations.

Future work will also include additional

validation of the model. We would like to validate

the model on a larger number of patients and

compare our methodology to other approaches.

4.2 Concluding Remarks

The system that has been presented in this paper,

which uses a Dynamic Bayesian Network approach

to modelling glycaemia in critically ill patients,

shows great promise. The system performs

extremely well in the context of great uncertainty,

sparse observations and limited system knowledge.

Our approach demonstrates a principled

technique for using standard real-time measurements

from ICU patients, to recalibrate model parameters

from general values to patient-specific values. This

model has the potential to be used by physicians to

individualise insulin dosage or to be incorporated

into a control system to automate insulin delivery.

The approach demonstrated here is applicable to

other applications where unseen variables must be

assessed and individualized in real-time.

Finally, the methodology introduced in this

paper, for mapping a system of differential equations

directly to a DBN, can be applied to other systems of

differential equations where all model terms vary,

and both continuous and sporadic temporal evidence

must be incorporated for an accurate solution.

ACKNOWLEDGEMENTS

We are grateful to the UHG Research Ethics

Committee for granting permission to extract

historical records from the database in the ICU of

University Hospital Galway. We acknowledge the

contributions of Dr Petri Piiroinen to the research

project overall and his feedback on this paper. This

research has been supported by Science Foundation

Ireland under grant 08/RFP/CMS1254, and by a

Marie Curie Transfer of Knowledge Fellowship of

the EU 6th Framework Programme contract CT-

2005-029611.

REFERENCES

Abkai, C. & Hesser, J., 2009. Virtual intensive care unit

(ICU): real-time simulation environment applying

hybrid approach using dynamic Bayesian Networks

and ODEs. Studies in Health Technology and

Informatics, 142, 1-6.

Aleks, N., Russell, S., Madden, M.G., Morabito, D.,

Staudenmayer, K., Cohen, M., Manley, G., 2008.

Probabilistic detection of short events, with

application to critical care monitoring. Proceedings of

NIPS 2008: 22nd Annual Conference on Neural

Information Processing Systems, Vancouver, Canada.

Andersen KE, Højbjerre M., 2003. A Bayesian approach

to Bergman’s minimal model. In C. M. Bishop and B.

J. Frey (eds), Proceedings of the Ninth International

Workshop on Artificial Intelligence and Statistics, Jan

3-6, 2003, Key West, FL.

Bergman, R.N., Phillips, L.S. & Cobelli, C., 1981.

Physiologic evaluation of factors controlling glucose

tolerance in man: measurement of insulin sensitivity

and beta-cell glucose sensitivity from the response to

intravenous glucose. Journal of Clinical Investigation,

68(6), 1456–1467.

Charitos, T., Van der Gaag, L.C., Visscher, S., Schurink,

K.A. & Lucas, P.J., 2009. A dynamic Bayesian

network for diagnosing ventilator-associated

pneumonia in ICU patients. Expert Systems with

Applications, 36(2P1), 1249–1258.

Chase J, Shaw G, Wong X, Lotz T, Lin J, Hann C., 2006.

Model-based glycaemic control in critical care—A

review of the state of the possible. Biomedical Signal

Processing and Control, 1(1), 3-21.

Van Gerven, M.A., Taal, B.G. & Lucas, P.J., 2008.

Dynamic Bayesian networks as prognostic models for

clinical patient management. Journal of Biomedical

Informatics, 41(4), 515-529.

Haverbeke N, Van Herpe T, Diehl M, Van den Berghe G,

De Moor B, 2008. Nonlinear model predictive control

with moving horizon state and disturbance estimation

– application to the normalization of blood glucose in

the critically ill. Proceedings of the 17th IFAC World

Congress 2008.

Hovorka, R., Chassin, L.J., Ellmerer, M., Plank, J. and

Wilinska, M.E.:,2008. A simulation model of glucose

regulation in the critically ill. Physiological

Measurement, 29, 959-978.

Iserles, Arieh, 2009. A first course in the numerical

analysis of differential equations. Second edition.

Cambridge Texts in Applied Mathematics. Cambridge

University Press, Cambridge.

Lin, J., Lee, D., Chase, J., Shaw,G., Le Compte, A., Lotz,

T., Wong, J., Lonergan, T., Hann, C.,2008. Stochastic

modelling of insulin sensitivity and adaptive glycemic

control for critical care. Comput. Methods Prog.

Biomed., 89(2), 141-152.

Russell, S. & Norvig, P., 2002. Artificial Intelligence: A

Modern Approach (2nd Edition), Prentice Hall.

The NICE-SUGAR Study Investigators, Finfer S, Chittock

DR, Su SY, Blair D, Foster D, Dhingra V, Bellomo R,

BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing

458

Cook D, Dodek P, Henderson WR, Hébert PC,

Heritier S, Heyland DK, McArthur C, McDonald E,

Mitchell I, Myburgh JA, Norton R, Potter J, Robinson

BG, Ronco JJ. et al., 2009. Intensive versus

Conventional Glucose Control in Critically Ill

Patients. New England Journal of Medicine, 360(13),

1283-1297.

Van Herpe, T., Espinoza, M. & Haverbeke, N., De Moor,

B., Van den Berghe, G.2007. Glycemia prediction in

critically ill patients using an adaptive modeling

approach. Journal of Diabetes Science and

Technology, 1(3), 348-356.

Van den Berghe, G., P. Wouters, P. ,Weekers, F.,

Verwaest, C., Bruyninckx, F., Schetz, M., Vlasselaers,

D., Ferdinande, P., Lauwers, P., Bouillon, R., 2001.

Intensive Insulin Therapy in Critically Ill Patients. N

Engl J Med, 345(19), 1359-1367.

APPENDIX 1: THE ICU-MM

Van Herpe et al. (2007) define the model terms as:

G: Glucose concentration in blood plasma.

: The insulin concentration in blood

plasma.

X: The effect of insulin on net glucose

disappearance. X is proportional to the

insulin in the remote compartment.

: The remote insulin. This variable does not

have a strictly defined clinical

interpretation but can be approached by

the fraction of insulin concentration

derived from the endogenous insulin

secretion.

: The basal value of plasma glucose.

: The basal value of plasma insulin.

and F

: The intravenous rate of insulin and

glucose are the two input variable to the

model.

: The glucose distribution space.

: The insulin distribution volume.

: The glucose effectiveness (i.e. the

fractional clearance of glucose) when

insulin remains at basal level.

: The fractional rate of net remote insulin

disappearance.

: The fractional rate of insulin-dependent

increase.

γ: The proportion by which endogenous

insulin is released when glycaemia

exceeds a threshold.

h: The glucose threshold. When this

threshold is reached the endogenous

insulin is produced.

n: The time constant for insulin

disappearance.

β: An additional model coefficient to keep

units correct. β = 1 min.

α: A scaling factor for the second insulin

variable I

APPENDIX 2: NODE VALUES AS

USED IN THE DBN

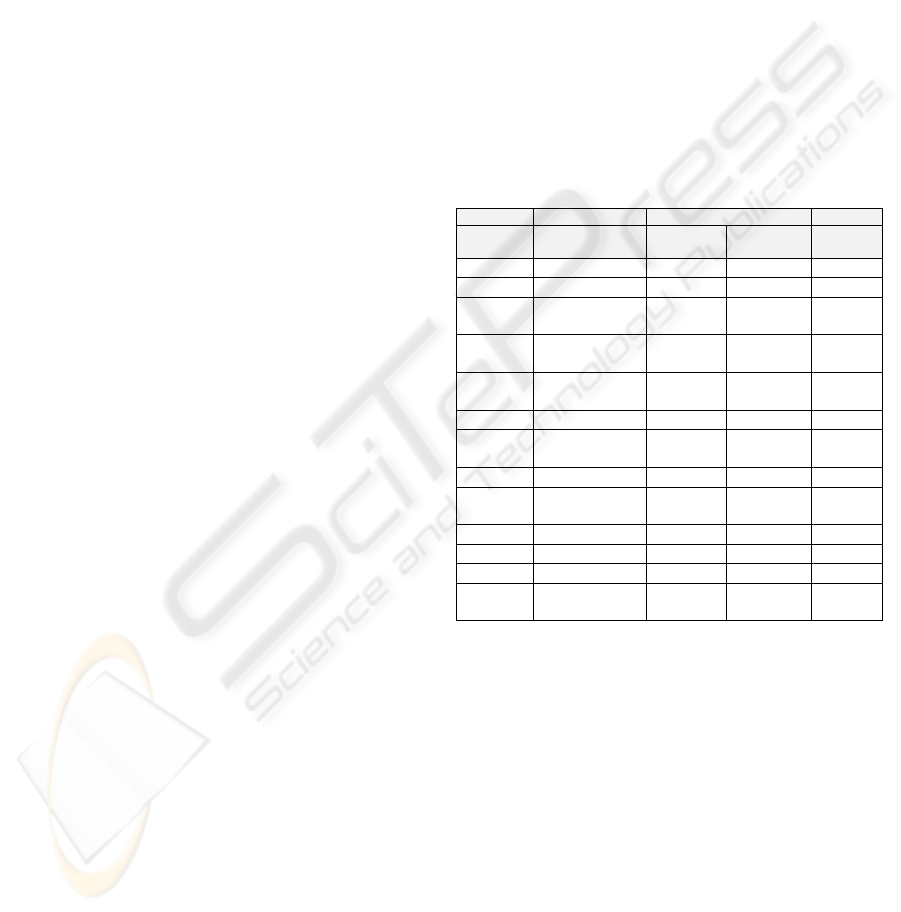
Table 1 below specifies the values set in the DBN

for the Gaussian nodes. Initially values were taken

from Haverbeke et al. (2008), subsequently G

and P

were modified.

Table 1: The means, standard deviations and limits for the

Gaussian nodes.

Node Mean Standard Deviation Range

Sensor

Model

Transition

Model

135 mg/dl 5 1 0+

10.7 μU/ml 1 0.1 0+

-0.0371

per min

0.005 0.005 -1:0

-0.0224

per min

0.002 0.002 -1:0

2.5E-5

ml/(min

μU)

2.0E-7 1.0E-6 0:1

h 107.4 mg/dl 30 10 0:360

N 0.2623

per min

0.1 0.001 0:1

Alpha 0.35 0.1 0.01 0+

Gamma 1.4001E-4

per min

1.0E-5 1.0E-5 0:1

Prescribed I 1 0+

Prescribed G 1 0+

Meas G G 5

Meas

Weight

Weight 0.1

The nodes V

and V

are modelled as

deterministic nodes. Their values are calculated as

1.6*Weight and 120*Weight respectively.

MODELLING GLYCAEMIA IN ICU PATIENTS - A Dynamic Bayesian Network Approach

459