CHARACTERIZATION OF MOLECULAR COMMUNICATION
CHANNEL FOR NANOSCALE NETWORKS
Mohammad Upal Mahfuz, Dimitrios Makrakis and Hussein Mouftah
Department of Electrical and Computer Engineering, School of Information Technology and Engineering (S.I.T.E.)
University of Ottawa, 800 King Edward Ave., Ottawa, ON, K1N 6N5, Canada
Keywords: Molecular communication, Propagation channel, Modeling, Pathloss, Bio-inspired nanonetworks,
Throughput, Channel quantum response.
Abstract: Recently molecular communication is being considered as a new communication physical layer option for
nanonetworks. Nanonetworks are based on nanoscale artificial or bio-inspired nanomachines. Traditional
communication technologies cannot work on the nanoscale because of the size and power consumption of
transceivers and other components. On the other hand, a detailed knowledge of the molecular
communication channel is necessary for successful communication. Some recent studies analyzed
propagation impairment and its effects on molecular propagation. However, a proper characterization of the
molecular propagation channel in nanonetworks is missing in the open literature. This goes without saying
that a molecular propagation channel has to be characterized first before any performance evaluation can be
made. Due to the nanoscale dimension of the nanomachines involved in molecular communication a
measurement based approach using in vitro experiments is extremely difficult. In addition, a proper tuning
of the experimental parameters is mandatory. This is why the authors were motivated to characterize the
‘channel quantum response (CQR)’ or equivalently the ‘throughput response’ of bio-inspired nanonetworks
with an alternative approach. This paper considers the molecular channel as particle propagation. The CQR
i.e. the throughput response and its characteristics have been found in order to better-understand the
molecular channel behavior of nanonetworks.
1 INTRODUCTION
Molecular Communication is a new interdisciplinary
field of research that has emerged from the
amalgamation of three independent research fields
named nanotechnology, biotechnology and
information and communication technology (ICT).
Molecular communication is one sub-division of the
large research area of nanoscale communication and
networking. Although scaling down of the macro-
devices leads to nanoscale components and
technologies in general, due to several practical
limitations of available technologies it has been
proposed that bio-inspired communications can
solve some key problems and thus nanoscale
molecular communication has become a good
candidate for the new molecular communication
based nanonetworking (Akyildiz, 2008, Lacasa,
2009). Communication in the form of concentration
encoding and molecular encoding as well as
networking among several nanomachines give rise
to nanonetworks. Nanomachines are artificial or
biological machines on the nanoscale dimensions (1
nm to 100 nm) responsible for extremely limited
tasks. Conventional artificial dry techniques have
several difficulties especially in the fabrication
phases, for which bio-inspired communication
techniques started to have been investigated very
recently (Atakan and Akan, 2007, Moritani et al.,
2006,
Parcerisa and Akyldiz, 2009, Moore et al.,
2009). Bio-inspired communication systems are
derived from molecular biology and biotechnology.
In addition to this, their advantages are realized
when nanotechnology and information and
communication technologies are brought together to
integrate into technologies based on molecular
communications, giving rise to the new field of
nano-bio-communication technology. Molecular
communication is in fact quite common in the nature
in living organisms as a means to communicate with
each other by enabling one or more biological
phenomena. Short-range molecular communication
327
Upal Mahfuz M., Makrakis D. and Mouftah H. (2010).
CHARACTERIZATION OF MOLECULAR COMMUNICATION CHANNEL FOR NANOSCALE NETWORKS.
In Proceedings of the Third International Conference on Bio-inspired Systems and Signal Processing, pages 327-332
DOI: 10.5220/0002757303270332
Copyright
c
 SciTePress

based on concentration encoding and long-range
communications based on pheromones are some
examples to mention (Akyildiz, 2008, Lacasa,
2009). Received molecular concentration or even
the transmitted molecules bound with the chemical
receptors on the cell boundary of nanomachines
contain biologically meaningful information which
triggers one or more biological phenomena to
perform the required task. Biological systems found
in nature perform both intra-cellular communication
through vesicles transportation and inter-cellular
communication through neurotransmitters, as well as
inter-organ communication through hormones
(Atakan, 2008). Molecular nanonetworks are in fact
quite significant in the sense that communication
and networking among a large number of
nanomachines can create several new applications,
for instance nanoscale distributed computation
systems, nanoscale bio-inspired or hybrid sensing
systems, improved health care systems,
nanomedicine, chemical sensor networks for micro-
nanoscale applications are just a few applications to
mention.
There exists some related research in the area of
molecular communication in the last few years. For
instance, Atakan (2007) discussed an information
theoretical approach for a molecular communication
systems based on several infeasible assumptions
(Lucasa, 2009). Akyldiz (2008) presented a survey
of nanonetworks with an emphasis on bio-inspired
molecular communications for short-range and long-
range communications. To the best of our
knowledge none of the papers in the open literature
has considered the molecular propagation channel
from particle propagation perspective and
investigated the channel behavior of the same. This
has given us the main impetus to write this paper.
Section-2 explains the channel behavior in terms of
channel quantum response (CQR). Some remarks
are mentioned and comments are made on the
findings. Finally, section-3 concludes the paper with
several future research directions.
2 PERFORMANCE
EVALUATION
2.1 Channel Quantum Response
(CQR) Modeling
The idea of CQR for molecular propagation channel
in nanonetworks came in fact from the well-known
time-dependent solution to concentration of diffused
substance as governed in macroscopic level by
Fick’s law and well documented in Bossert (1963)
and Berg (1993). However, the same idea could be
suitable for nanonetworks, too. Unlike RF
propagation, molecular propagation should be
treated with the quantum or particle theory of
propagation. CQR is in fact to some extent
analogous to channel impulse response (CIR) of
traditional communication systems. For example, the
number of molecules received from a point source
per unit of volume can be calculated from the well-
known Roberts equation (Bossert, 1963) as
()
()
2
4
3
2
,
4
π
−
=⋅
r
D
t
Q
Urt e
Dt
(1)
where r is the distance of the receiver from the
emitting source, Q is the amount of released
molecules per second and D is the diffusion constant
in cm
2
/s unit. D depends on the medium through
which the molecules propagate. To the best of our
knowledge, there isn’t any work in the open
literature that has made an effort to extract and
define the CQR or equivalently to the throughput.
This has given us the main impetus for writing this
paper. The CQR and its characteristics could be
deduced from (1). The propagation of information
molecules in a molecular channel in shown in Fig.1.
In order to determine CQR, the molecular channel is
excited by an instantaneous short duration quanta
emission of molecules Q(t) for a given time duration
t
H
as shown in Fig.2. Since molecule transmissions
in biological nanomachines are in fact slow
processes, to make it more practical we consider
Q(t)=Q for a duration of t
H
where we also vary t
H
as
shown in Fig.2. Considering the generalized Q(t)
eqn. (1) can be written as (Bossert, 1963)
()
()
()
{}
()
2
4
3
0
2
,
4
τ
τ
τ
πτ
−
−
=⋅
−
∫
r
t
Dt
Q
Urt e d
Dt
(2)
which for our purpose, can be re-written as
()
()
()
{}
()
() ()
2
4
3
0
2
,
4
H
r
t
Dt
Q
Urt e d Qt gt
Dt
τ
τ
τ
πτ
−
−
=⋅=⊗
−
∫
(3)
where
()
()
2
4
3/2
4
r
Dt
e
gt
Dt
π
−
=
(4)
is defined as the CQR of the molecular channel and
the symbol ⊗ indicates convolution operation. In
this paper we have made a rigorous analysis of this
CQR. Please note that propagation impairments are
not considered for the time being, but indicated as
future works. Fig.1. shows a generalized molecular
communication channel, the blue circles
representing the molecules transmitted by the
BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing
328

transmitter nanomachine (TN), propagated in the
channel, and finally received by the receiver
nanomachine (RN).
Figure 1: Propagation of information molecules: A
generalized molecular propagation channel between a
transmitter nanomachine (TN) and a receiving
nanomachine (RN).
Figure 2: Input concentration excitation: practical case,
when for t
H
→0 ideal quantum excitation for concentration
encoding is realized, the area (in shaded region) being
constant.
The reasoning behind the idea that g(t) is
considered as the channel quantum response is
similar to what is found in the propagation of
electromagnetic (EM) wave. However, g(t) must not
be termed as channel impulse response (CIR), the
reasoning being that unlike EM wave molecular
propagation is based on particle (molecule)
propagation. The modes of propagation can be
concentration encoding where the concentration
level is considered as the carrier signal, or molecular
encoding where individual molecule is engineered
such that its internal structure is altered and so it
itself becomes a carrier and carries specific
information. This is why the consideration of g(t)
here as ‘CQR’ or ‘throughput response’ is justified.
However, it is to be noted here that CQR g(t) is
independent of the input molecular concentration
Q(t). This has made our reasoning to consider g(t) as
channel quantum response (CQR) more solid. Please
note that CQR can also be termed as ‘throughput
response' as an equivalent term.
2.2 Distance and Temporal
Dependence
As shown in eqn. (4) the CQR is a function of both
time, t and distance, r from the transmitting
nanomachine (TN). Investigating into g(t) it is clear
that unlike EM wave propagation modeling the
molecular communication channel cannot be
explained in terms of separate distance dependence
and temporal dependence. The numerator in eqn. (4)
is a function of both distance r and time t. In free
space EM waves propagate at the speed of light
(3×10
8
m/sec). In some cases wireless channels are
realistically assumed to be stationary for short
propagation times between sender and receiver. But
unlike EM propagation molecular propagation is a
very slow process and so the temporal variation of
CQR cannot be ignored even for short distances on
the nanoscale. The temporal variation rather plays a
significant role in terms of pathloss and throughput
analysis. In the next section an expression has been
derived for the pathloss for a molecular channel. As
mentioned, the concentration of molecules at a
distance r and at time t i.e. U(r,t) is analogous to the
energy of the molecular propagation. So the rate of
change of concentration over time i.e. dU/dt would
be analogous to power of EM signal. As a result it is
important to have the g(r,t) energy normalized to the
available total molecular energy. Figure 3 below
shows the normalized CQR g(r,t) over a time of 250
seconds for a specific TN-RN distance of 2 cm.
Figure 3: Normalized CQR i.e. throughput for molecular
propagation channel.
It should be noted that in this paper we have been
motivated to use the term ‘throughput’ rather than
TN
RN
Information
molecules
Molecular Propagation Channel
t
L
→
∞
t
H
→ 0
Δt
0
Q
t
Δ
(b)
0
t
(
s
)
Q
Area =
0
Q
t
(
s
)
t
H
Q (molecules/sec)
0
H
Q
t
t
L
Area =
0
Q
(a)
0
CHARACTERIZATION OF MOLECULAR COMMUNICATION CHANNEL FOR NANOSCALE NETWORKS
329

‘output’ when referring to U(r,t) because molecular
propagation is not a wave propagation, it is rather
the molecules themselves moving from TN to RN.
Note that for ideal case when Q(t)=
δ (t) the CQR
g(r,t) actually represents the throughput of the
channel, i.e. U(r,t)=g(r,t). In that sense Fig.3 also
represents the throughput response of the molecular
channel. The variation of the energy normalized
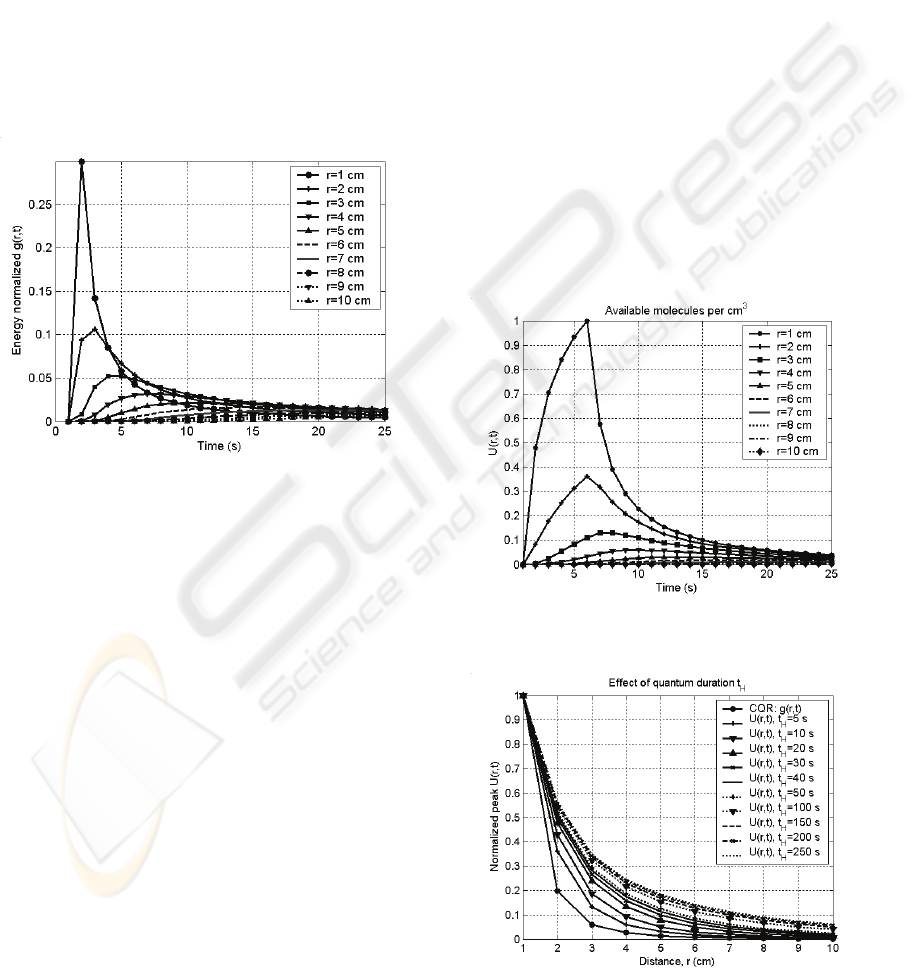
CQR g(r,t) for different distances in shown in Fig.4.
Energy normalized CQR is of significant importance
because of the fact that it indicates the amount of
pathloss in the form of concentration loss in
propagation for different TN-RN distances. This
distance dependence of normalized CQR g(r,t) can
be used to derive the expression of pathloss as
shown in section 2.4.
Figure 4: Comparison of energy normalized g(r,t) i.e.
throughput (i.e. concentration output) profile of the unicast
molecular channel.
As expressed in eqn. (3) the throughput U(r,t) of
a molecular channel depends on Q(t). For ideal case
when Q(t)=
δ (t) the throughput is U(r,t)=g(r,t).
However, for all practical purposes an impulsive
Q(t) is not possible. So, practical values of Q(t) as
shown in Fig.2 are considered where the average
number of transmitted molecules Q(t) occurs over
the duration t
H
seconds. The throughputs for
different TN-RN distances from 1 cm to 10 cm are
shown in Fig. 5. As shown in Fig.5 the molecules
available for reception at the RN are significantly
reduced as the distance increases. It should be noted
that Fig. 5 shows the molecules available at receiver
only, not the molecules received by the receiver.
This is because reception by the receiver depends on
several other factors including principally the
affinity of information molecules to the receptor of
the receiving nanomachine RN. This paper deals
with the molecules available for receiving only,
while the details of reception mechanism are beyond
the scope of this paper.
Throughput depends also on the duration t
H
of
molecular transmission. As shown in Fig.2 the ideal
situation occurs when
Δ t=0, which is impractical.
For our purposes we have assumed a fixed amount
molecules Q
0
which are transmitted at an average
rate of Q
0
/t
H
molecules per second over the duration
of t
H
seconds. As a result the total number of
transmitted molecules Q
0
is analogous to the strength
of an impulse in traditional impulse response
analyses. The normalized peak throughputs U(r,t)
for different TN-RN distances and different
transmission duration t
H
have been shown in Fig.6.
The throughput gains have been shown in Table 1.
Referring to Fig. 6 as shown in Table 1 increasing
the value of t
H
gives a gain in peak value of U(r,t),
i.e. increased number of molecules are received even
if the distance is unchanged (r=3 cm for Table 1).
However, it is also found that there is a decreasing
relative gain (in dB/octave) when we double the
transmission duration t
H
while keeping the distance r
unchanged.
Figure 5: Available molecules per cm
3
at distance r with
duration t
H
=5 seconds.
Figure 6: Peak variation of CQR g(r,t) and throughput
U(r,t).
BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing
330

Table 1: Throughput U(r,t) gain for different t
H
at r=3 cm.
t
H
=0
sec
t
H
=5
sec
t
H
=10
sec
t
H
=20
sec
U(r,t) 0.05 0.15 0.2 0.25
Gain
U
(
r,t
)
- 4.7 dB 6.02 dB 6.98 dB
Gain (dB/octave) - - 1.32 dB 0.96 dB
2.3 Throughput Delay Profile
As shown in eqns. (3) and (4) the CQR can also be
termed as the throughput since U(r,t) actually shows
the molecules per unit volume (cm
3
) at a distance r
at time t. In traditional wireless communications the
term ‘output’ is analogous to the term ‘throughput’
here in molecular communication (i.e. molecular
concentration in this case). That is why in the similar
way what is known as the ‘pathloss’ in traditional
wireless communication is analogous to
‘concentration loss’ in molecular communication.
An expression of pathloss is derived in the next
section. In order to characterize any communication
channel the conventional approach finds channel
gain and channel delay.
A way to characterize the delay profile of a
molecular communication channel is to find out its
mean excess delay and RMS delay spread using the
channel quantum response (i.e. throughput
response). In this research efforts are made to come
up with mean excess delay and RMS delay spread
values for a unicast molecular channel and the
results are shown in Fig.7 and Fig.8 respectively. An
observation time of 250 seconds has been considered
because this is a reasonably sufficient observation
time, provided that referring to Fig. 3 and Fig. 4,
almost all the channel energy are located within 25
seconds of the observation (i.e. 1/10
th
of 250
seconds). The time-step considered in our simulation
was 1 second.
Figure 7: Excess delay characteristics for air medium.
Figure 8: RMS delay spread characteristics for air
medium.
2.4 Pathloss Modeling
In this section a pathloss expression has been
computed using the distance and time dependent
CRQ g(r,t). It is already shown earlier that in the
ideal case when the input is Q(t)=
δ (t) the throughput
of a molecular communication channel is given by
U(r,t)=g(r,t). So according to eqn. (4) the available
molecular concentrations at distances r
1
and r
2
from
the transmitting nanomachine TN where r
2
>r
1
are
given as
()
()
2
1
2
2
4
1
3
2
4
2
3
2
(,)
4
(,)
4
r
Dt
r
Dt
e
Urt
Dt
e
Urt
Dt
π
π
−
−
=
=
(5)
Pathloss in molecular communication can be
defined as the loss of concentration (in the case of
concentration encoding). The molecules are diffused
from TN to RN through the channel. At any time
instant t and distance r the molecular concentration
U(r,t) represents the bit information. Using eqn. (5)
pathloss in molecular communication can be
expressed as
2
1
4
10 10
2
(,)
()10log 10log
(,)
r
D
t
Urt
PL dB e
Ur t
⎛⎞
⎛⎞
==
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
(6)
where the TN is located at
1
0r = and the molecules
are available at a distance
2
rr=
. In contrast to the
conventional wireless communication systems the
molecular communication is a very slow process, so
there is a high probability that the channel suffers
CHARACTERIZATION OF MOLECULAR COMMUNICATION CHANNEL FOR NANOSCALE NETWORKS
331

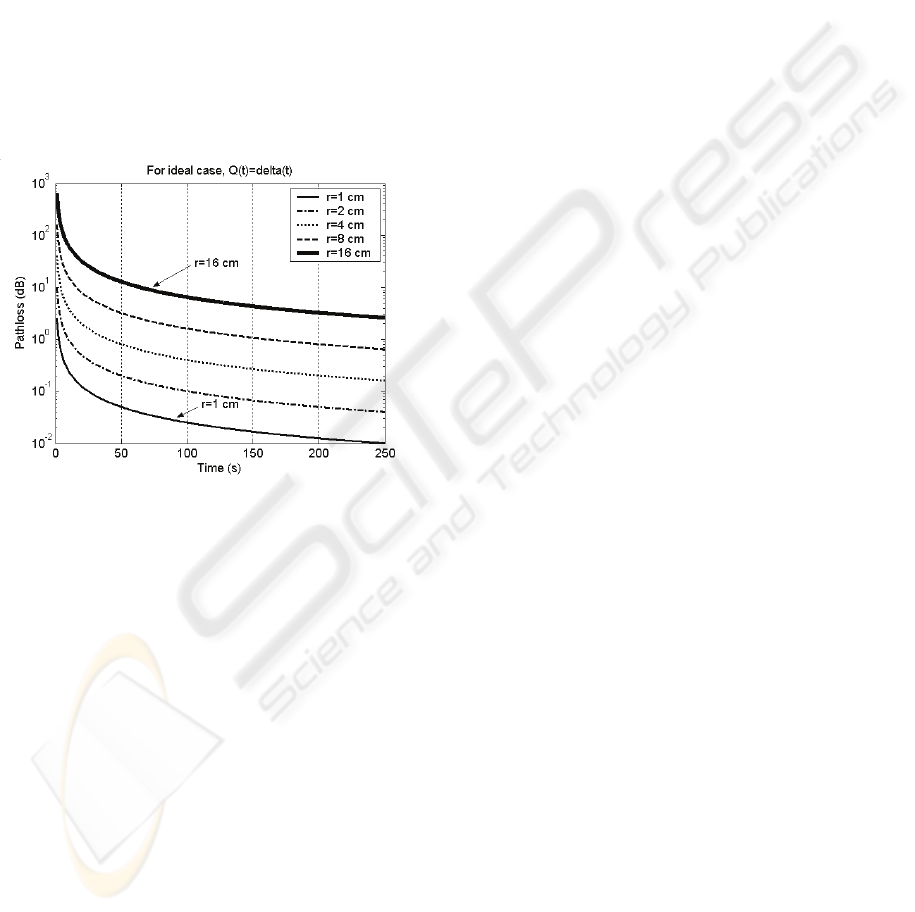
from pathloss. This is how it is shown in the pathloss
equation above that the pathloss is a function of both
distance r and time t and both of these two variables
have to be handled simultaneously. This makes the
pathloss in molecular communication a bit
complicated by not being able to express it as a
function of distance only. The pathloss for different
distances as a function of time are shown in Fig. 9.
Initially there is a high pathloss because when the
TN starts transmitting the molecules, there is no
molecules available at the RN side as being a slow
process it takes some time for the molecules to
propagate from TN to RN. After a long time
transmitted molecules reach the intended RN and so
the pathloss decreases with time. This indicates the t
in the denominator in the power of exp(r
2
/4Dt) in
eqn. (6).
Figure 9: Pathloss as a function of time t for different
distances r from TN.
3 CONCLUSIONS
In this paper we have developed an analytical
approach for getting the channel quantum response
(CQR) or equivalently the throughput response for
molecular communication. This analysis contributes
to the recent research of molecular propagation
channel modeling and subsequent analyses. An
analytical approach is useful in the sense that real
propagation of molecular communication is very
difficult due to extremely small (nano) scale of
dimensions and experimental requirements. In such
cases if a molecular propagation channel could be
characterized analytically then the results would
become very handy to analyze such a propagation
channel without actually waiting for analyses with
real molecular data and in vitro experiments. The
approach presented in this paper is based on the
spatial and temporal distribution of received
concentration of the information molecules in a
given propagation medium. Two things to be noted
regarding the diffusion coefficient parameter D,
firstly, it is assumed that the diffusion coefficient D
remains constant during the period of analysis. This
is validated by several open literature in this area.
Also it is to be noted that propagation in air is
considered (D=0.43) in this paper. However, similar
results in aqueous medium e.g. water, blood plasma
can also be obtained. Please note that different
values of the diffusion coefficient D of the
propagation media characterize differently the
Brownian motion of information molecules in
different media. As a second thought, the effects of
the information molecules themselves on the
propagation are not considered for now but are left
as the on-going part of our current research.
Statistical analyses of the results obtained in this
paper are also one of our recent research works in
this area.
REFERENCES
Akyildiz, I. F., Brunetti, F., Blazquez, C., 2008.
NanoNetworking: A New Communication Paradigm.
Computer Networks Journal (Elsevier), Vol. 52, pp.
2260-2279, August, 2008.
Atakan, B., Akan, O. B., 2007. An Information
Theoretical Approach for Molecular Communication.
In IEEE/ACM Bionetics, Budapest, Hungary,
December.
Berg, H. C., 1993. Random Walks in Biology, Princeton
University Press.
Bossert, W. H., 1963. Analysis of Olfactory
Communication among Animals. Journal of
Theoretical Biology, pp.443-469.
Lacasa, N. R., 2009. Modeling the Molecular
Communication Nanonetworks. M.Sc. thesis, The
Universitat Politècnica de Catalunya (UPC), Spain,
January.
Moritani, Y., Hiyama, S., Suda, T., 2006. Molecular
Communication for Health Care Applications. In
Fourth IEEE International Conference on Pervasive
Computing and Communications Workshops, pp. 549-
553, March.
Moore, M. J., Suda, T., Oiwa, K., 2009. Molecular
Communication: Modeling Noise Effects on
Information Rate. IEEE Trans. on Nanobioscience,
vol. 8, no. 2, pp. 169-180, June.
Parcerisa, L., Akyildiz, I. F., 2009. Molecular
Communication Options for Long Range
Nanonetworks. to appear in Communication Networks
(Elsevier) Journal, UK.
BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing
332