TWO-POPULATION GENETIC ALGORITHM

An Approach to Improve the Population Diversity

M. Gestal, D. Rivero, E. Fernández, J. R. Rabuñal and J. Dorado

Department of Information and Communications Technologies, University of A Coruña, Spain

Keywords: Evolutionary Computation, Diversity, Genetic Drift.

Abstract: Genetic Algorithms (GAs) are a technique that has given good results to those problems that require a

search through a complex space of possible solutions. A key point of GAs is the necessity of maintaining

the diversity in the population. Without this diversity, the population converges and the search prematurely

stops, not being able to reach the optimal solution. This is a very common situation in GAs. This paper

proposes a modification in traditional GAs to overcome this problem, avoiding the loose of diversity in the

population. This modification allows an exhaustive search that will provide more than one valid solution in

the same execution of the algorithm.

1 INTRODUCTION

Based on natural evolution, Evolutionary

Computation (EC) tools have shown to be very

efficient techniques when solving different

problems. One of these techniques, Genetic

Algorithms (GAs), is used mainly for the

optimization of a set of parameters (Fogel, 2006).

All of the EC techniques are based on the same

principles: an initial random population is made to

evolve by means of genetic operators (crossover and

mutation) inspired in Biology.

This evolution is done until a stop criterion is

fulfilled like maximum number of generations, a

MSE threshold or the convergence of the population.

But, if the population has a low diversity, i.e. the

population is very homogeneous, resulting in having

many individuals very similar, or identical. This

leads to having the crossover operator very

inefficient, because it builds new solutions that

explore areas of the search space that have already

been explored by other solutions. Therefore, only the

mutation operator can introduce new diversity in the

population. This all leads to a big loss of efficiency

in the whole algorithm, and it is a very common

problem in GAs (Zaharie, 2003).

Another problem due to the lack of diversity

appears when problems with multiple valid solutions

(or solutions with a very similar fitness) are trying to

be solved (multimodal problems). In these cases a

traditional GA will try to keep in the populations

values corresponding only to one of these solutions.

2 EVOLUTIONARY

APPROACHES TO INCREASE

DIVERSITY

As already stated, the diversity lack leads to an

efficiency and efficacy loss. Even this diversity lack

is very common on later stages of the evolution, its

appearance on the early generations is a very

important problem that affects the whole search. To

avoid this problem, different strategies have been

proposed, most of them based on heuristics.

First, some of the approaches try to solve this

problem by means of the dynamic variation of

crossover and mutation rates (Ursem, 2002). A

diversity measure is needed to control this problem,

which allows changing dynamically the mutation

and crossover rates.

New crossover algorithms have also been

proposed to solve this problem. Some of them are

BLX (Blend Crossover), SBX (Simulated Binary

Crossover), PCS (Parent Centric Crossover), CIXL2

(Confidence Interval Based Crossover using L2

Norm), UNDX (Unimodal Normally Crossover) or

fuzzy recombination (Lozano, Herrera and Cano,

2008).

Different approaches in replacement algorithms

have also been proposed to avoid diversity loss. En

example of this is Crowding algorithm. This

635

Gestal M., Rivero D., Fernández E., Rabuñal J. and Dorado J. (2010).

TWO-POPULATION GENETIC ALGORITHM - An Approach to Improve the Population Diversity.

In Proceedings of the 2nd International Conference on Agents and Artiﬁcial Intelligence - Artiﬁcial Intelligence, pages 635-639

DOI: 10.5220/0002760306350639

 SciTePress

algorithm began as a deterministic approach, but

also a probabilistic version has been published, in

which individuals compete in a probabilistic

tournament (M

engshoel and Goldberg, 2008).

Species-based are also used when the problem

requires an in-depth search over the solution space.

In this case, the solution to the lack of diversity is

simulated adding new populations, but the problem

remains within each of these populations (Nicholson

and White, 2008).

The main inconvenience of the techniques

previously described (replacement and crossover

operators) lies in the fact that they add new

parameters that should be configured according the

process of execution of GA. This process may be

disturbed by the interactions among those

parameters (Bäck, Eiben and van der Vaart, 2002).

3 TWO-POPULATION GENETIC

ALGORITHM

In this work a novel approach is presented to

preserve the genetic diversity. It tries to keep the

diversity stable by means of the use of a new

population that works as repository information.

This repository will allow the GA to be able to

create solutions all over the search space. In this

way, the population diversity does not reduce over

the time.

3.1 General Structure

The lack of diversity of the genetic population is the

key feature which will lead to improving efficacy

and efficiency. To do this, a new population is added

to the traditional GA. This population is called

genetic pool, and it forces a homogeneous search

through the search space.

This genetic pool divides the search space into

sub-regions (see Fig. 1), because each individual has

its own fenced range for gene variation, i.e., each

gene of each individual can take values only inside a

limited rank. Therefore, each individual of the

genetic pool represents a sub-region of the search

space, and the whole search space is divided into all

of the individuals of this genetic pool.

Depending on both type and complexity of the

problem that it is intended to solve, the user has to

set the number of sub-regions that require into the

search space. It should be borne in mind that a

traditional GA performs its search only one sub-

region (the whole of the search space).

Figure 1: Sample of Genetic Pool configuration.

The secondary population works as a classical

population, i.e., no additional rank restrictions are

introduced in this population (each individual’s

genes can take values all over the search space). Its

only variation refers to the application of crossover

and mutation operators, which operate between both

populations (explained below).

This secondary population contains the solutions

to the problem, whereas the genetic pool acts as a

support, keeping the search space homogeneously

explored and a diverse population.

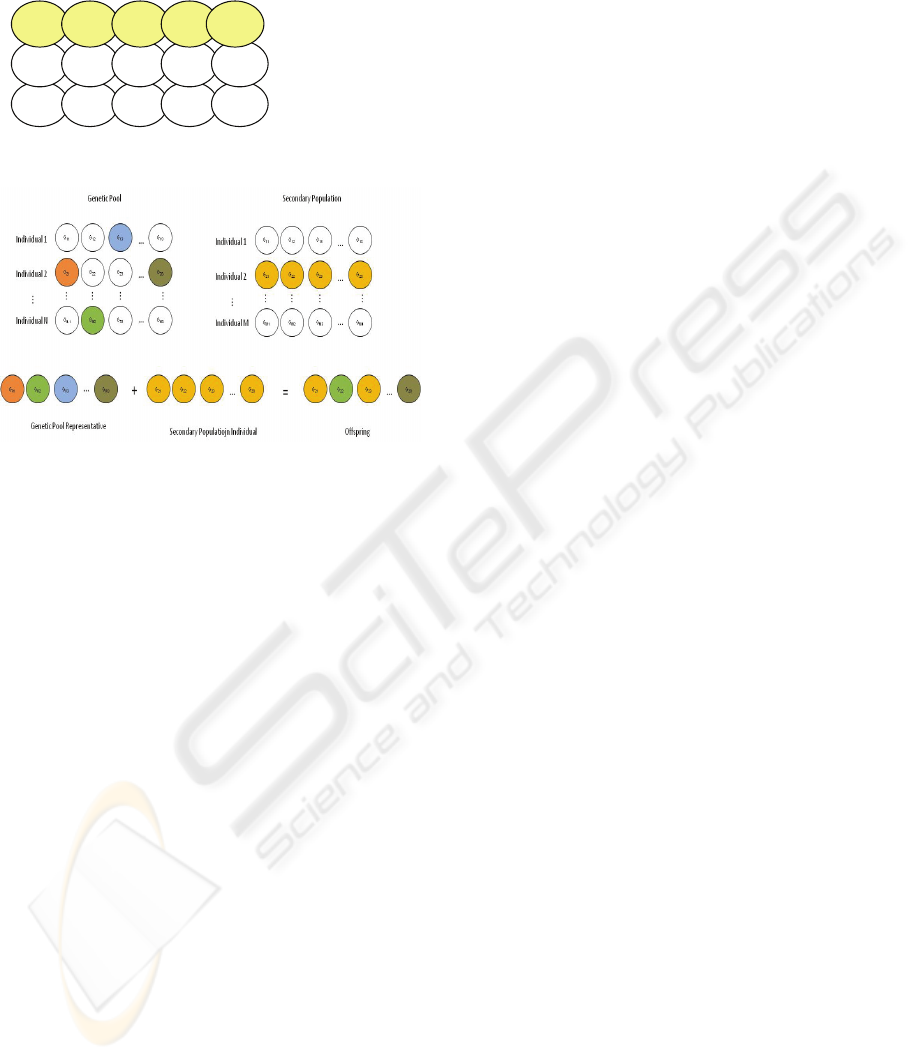
3.1.1 Genetic Pool

The main objective of the genetic pool is to allow

the GA to explore the whole search space with a

homogeneous search. As each individual in the

genetic pool represents a sub-region of the global

search space, it has the same structure or gene

sequence than when using a traditional GA.

But these individuals need some extra information

(see Fig. 2). First, in a traditional GA population

these genes can take any valid values, but in the

genetic pool the genes can take values only in a

restricted range (different for each individual). The

total range values are divided into the same number

of parts than individuals in genetic pool, so that a

sub-range of values is allowed to each individual.

Those values that a given gene may have will remain

within its range for the whole of the performance of

the proposed GA. Therefore, if the genetic pool has

a size of N individuals, the whole search space is

partitioned into N parts of the same size, each of

them represented by an individual of the genetic

pool.

In addition of this partition, every individual in

the genetic pool knows which of its genes are part of

the best solution found up to then, i.e., genes that

belong to the best individual in the secondary

population. This flag is used to avoid the

modification of those genes that are the best solution

to the problem.

Also, each gene in each individual in the genetic

pool has a value that indicates the relative increment

N.1

Individual1

Individual2

Indiv idual10

[0..1)

[1..2)

[9..10]

[0..2)

[2..4)

[18..20]

…

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

636

that would be applied to the gene during a mutation

operation (the I value). This mutation operator is

described below.

Figure 2: Genetic Pool individual.

Figure 3: Crossover operation.

An important thing to bear in mind is that these

individuals do not represent global solutions to the

problem. Therefore, their fitness value is useless and

no computational time is wasted in this task.

3.1.2 Secondary Population

The individuals in the secondary population are

similar than those of a traditional GA population,

i.e., they can adopt values throughout the whole of

the solutions area. In this way, they offer global

solutions to the problem, which is something that

none of the individuals of the genetic pool is able to

do due to the range restriction. Therefore, this

population contains the solutions to the problem and

performs an evolution similar to a classical GA

population, with some differences in the genetic

operators (crossover and mutation).

3.2 Genetic Operators

3.2.1 Crossover

The crossover operator has been modified in order to

operate between individuals in the secondary

population (using complete solutions to the problem)

and the genetic pool. This operator now recombines

genetic material from two parents, each of them

from each population.

First, an individual is randomly chosen from the

secondary population. Therefore, there is no need to

have this population organized attending to the

fitness value of its individuals.

The Representative is also built from the genetic

pool. This representative is assembled by randomly

choosing the genes from the individuals of the

genetic pool (see Fig. 3).

These two individuals (the randomly chosen from

the secondary population and the representative

from the genetic pool) will be the parents in the

crossover operation. A uniform crossover is

performed between these two parents. As a result of

this crossover, only one individual is generated after

the random selection of every one of its genes from

both ancestors.

A non destructive replacement algorithm has been

used in order to insert this new individual into the

secondary population. This insertion is performed

when the fitness of the offspring is better that the

fitness of the selected parent from the secondary

population. Therefore, if the new individual

represents the new best solution, the genes of the

representative individual in the genetic pool

(Boolean values B

at Fig. 2) are consequently

marked in the corresponding individuals of the

genetic pool.

3.2.2 Mutation

The mutation operator only modifies individuals in

the genetic pool. First of all, a random individual is

chosen from the genetic pool. A gene is chosen from

that individual and the specified increment value

associated to that gene is applied to it (the value I in

Fig. 2). The selected gene must not have the mark of

belonging to the best solution in the secondary

population, i.e., it should not have the Bi value

marked.

When the addition of current gene value plus the

increment exceeds the upper end of the sub-range in

which the gene may vary, this gene becomes the

lower value of the sub-range. Furthermore, if this

happens, the incremental value that is going to be

applied to subsequent mutations of that gene is also

reduced. This is done in order to perform a more

exhaustive search in all of the values that a gene

may adopt as the evolution process goes on.

4 EXPERIMENTS

In this section different experiments will show the

performance of the proposed system. A comparison

with traditional GAs is done in order to measure the

…

...

Genotype

Best solution control

IncrementalMutation

Value

TWO-POPULATION GENETIC ALGORITHM - An Approach to Improve the Population Diversity

637

goodness of applying this modification to the GA.

Different problems have been solved with this

system. First of all, some synthetic problems will be

used to assess the approach functioning. They will

allow to test whether the system proposed is able to

provide several valid solutions in the same run, and,

therefore if the population does not converge to a

single individual. The performance of the algorithm

proposed and the ability of finding different

solutions is studied with these problems, in

comparison with results obtained with traditional

GAs.

The preliminary tests tried to establish the level of

convergence and exhaustive search of the new

algorithm compared to the classic GA.

Among different test trials, the discrete function

represented in Fig. 4 was used to prove the proposed

system. This function takes values within the

interval [0..2] where several narrow local minimums

with value 0 have been added.

x f(x)

0.07 0.08

0.5 0.01

0.7 0.001

1.2 0.05

1.6 0.08

1.7 0.02

1.85 0.005

Figure 4: Test function.

Parallel executions of classical GA and the

proposed GA will be done until one of them reach a

threshold error, in this concrete case establish when

mse<0.05. Once the algorithm reach the threshold

the number of solutions kept in the solution is

annotated.

The main objective of this synthetic function is

to find out how the search space is explored in-

depth.

Each individual will codify five times the same

function, so five simultaneous runs will be

performed. It will allow to graphically checking the

minimum achieved and increase the complexity of

the individuals. To avoid possible constructive

blocks that make simpler the resolution of the

problem the fitness function will be the following

one:

Fitness = f(G

) + f(2-G

) + f(G

) + f(2-G

) + f(G

)

5 RESULTS

The Fig. 5 presents the results with the test function

represented in Fig 4. This graph shows the average

number of solutions kept inside the population

respect to the population size (number of

individuals). Different genetic pool sizes were taken,

from 1 to 50 individuals, and the secondary

population size also changed between 2 and 50

individuals. The population size in the classical GA

has also been changed with sizes between 2 and 50.

For each configuration 50 runs were performed and

the mean values annotated.

This figure shows that the behaviour of the two-

population GA is better to the traditional GA. Even

the efficiency of the classical GA improves with

bigger populations, it does not reach the results

achieved by the two-population GA. More precisely,

the average number of solutions in the population of

the two-population GA was 5.5048 (over 7 possible

different solutions), while the average number in the

traditional GA was only 0.5216 (with a maximum in

0.92).

Figure 5: Population sizes and solutions found.

6 CONCLUSIONS

Several conclusions can be drawn from the results

obtained with the use of the system proposal. The

most important one is that it was able to keep the

population diversity over the execution of the

algorithm, the start point of this work. In the

problems presented, this behaviour allowed to keep

a number of solutions in the population greater than

the classical GA. So, the approach seems a

promising line where interesting results can be

finding.

In the proposed system the number of regions on

the genetic pool is fixed in advance. It would be

good to investigate different ways to allow it to

change dynamically. So, new operators (like region

gathering, division) would be interesting to explore.

Individuals within Genetic Pool

Individualswithin Secundary Population

Population Size

Solutions Found for the Two-Population GA

Genetic Pool Size

Secondary Population Size

Population Size

Solutions Found for the Classical GA

Local Minimums

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

638

REFERENCES

Bäck, T., Eiben, A.E., van der Vaart, N.A.L., 2002. An

Empirical Study on Gas Without Parameters, In

Proceedings of the 6th International Conference on

Parallel Problem Solving from Nature, p.315-324.

Fogel, F., 2006. Evolutionary Computation: toward a new

philosophy of machine learning. IEEE Press.

Lozano, M., Herrera, F., Cano, J.R., 2008. “Replacement

strategies to preserve useful diversity in steady-state

genetic algorithms”. Information Sciences, 178(23),

pp. 4421-4433.

Mengshoel, O.J, Goldberg, D.E., 2008. “The crowding

approach to niching in genetic algorithms”.

Evolutionary Computation, 16(3), pp 315-354.

Nicholson, J., White, M., 2008. Maintaining population

diversity by maintaining family structures.

Proceedings of 10th annual conference on Genetic and

evolutionary computation, pp. 533-534.

Ursem, R.K., 2002. Diversity-Guided Evolutionary

Algorithms, In Proceedings of VII Parallel Problem

Solving from Nature, pp. 462-471.

Zaharie, D., 2003. Control of population diversity and

adaptation in differential evolution algorithms. In

Proceedings of 9th International Conference Soft

Computing, Czech Republic, pp. 41–46.

TWO-POPULATION GENETIC ALGORITHM - An Approach to Improve the Population Diversity

639