LSVF: LEAST SUGGESTED VALUE FIRST

A New Search Heuristic to Reduce the Amount of Backtracking Calls in CSP

Cleyton Mário de Oliveira Rodrigues, Eric Rommel Dantas Galvão, Ryan Ribeiro de Azevedo

Centro de Informática, Universidade Federal de Pernambuco

Av. Professor Luís Freire, 50740-540 Recife, Pernambuco, Brazil

Marcos Aurélio Almeida da Silva

Paris Unviversitas, LIP06, 104 Avenue du Président Kennedy 75016 Paris, France

Keywords: Constraint Satisfaction Problem, Heuristics, Constraint Logic Programming.

Abstract: Along the years, many researches in the Artificial Intelligence (AI) field seek for new algorithms to reduce

drastically the amount of memory and time consumed for general searches in the family of constraint

satisfaction problems. Normally, these improvements are reached with the use of some heuristics which

either prune useless tree search branches or even “indicate” the path to reach the solution (many times, the

optimal solution) more easily. Many heuristics were proposed in the literature, like Static/ Dynamic Highest

Degree heuristic (SHD/DHD), Most Constraint Variable (MCV), Least Constraining Value (LCV), and

while some can be used at the pre-processing time, others just at running time. In this paper we propose a

new pre-processing search heuristic to reduce the amount of backtracking calls, namely the Least Suggested

Value First (LSVF). LSVF emerges as a practical solution whenever the LCV can not distinguish how much

a value is constrained. We present a pedagogical example to introduce the heuristics, realized through the

general Constraint Logic Programming CHR

, as well as the preliminary results.

1 INTRODUCTION

Constraint Satisfaction Problems (CSP) remains as

one of the most prominents AI research fields.

Having a wide range of applicability, such as

planning, resource allocation, traffic air routing,

scheduling (Brailsford, 1999), CSP has been largely

used either for toys or even for real large complex

applications. Furthermore, in general, CSP are NP-

complete and they are combinatorial in nature.

Amongst the various methods developed to

handle this sort of problems, in this paper, our focus

concerns the search tree approach coupled with the

backtracking operation. In particular, we address

some of the several heuristics used so far to reduce

(without guaranties) the amount of time need to find

an solution, namely: Static/ Dynamic Highest

Degree heuristic (SHD/DHD), Most Constraint

Variable (MCV) and Least Constraining Value

(LCV) (Russel & Norvig, 2003).

Some problems, however, like the ones common

referred as instances of the Four Color Map

Theorem (Robertson et. al, 1997), present the same

domain for each entity, making the LCV heuristic

impossible to decide the best value to the asserted

first.

For these cases, we propose a new pre-

processing heuristic, namely Least Constraint Value

First (LCVF), which can bring significant gains by a

simple domain value sorting, respecting an order

made by the following question “Which is the least

used value to be suggested now?”. Additionally, we

enumerate some assumptions to improve the

ordering. Along the paper, we show some

preliminary results with remarkable reduce of

backtracking calls.

This paper is organized as follows: Section 2

explains briefly the formal definition of CSP and the

most common heuristics used in the class of CSP;

following, Section 3 details what is CHR

and why

we have chosen it to our examples; Section 4

introduces the LCVF heuristic with a pedagogical

example, highlighting some preliminary results, and

finally, Section 5 presents the final remakes’ and the

future works.

416

Mário de Oliveira Rodrigues C., Rommel Dantas Galvão E., Ribeiro de Azevedo R. and Aurélio Almeida da Silva M. (2010).

LSVF: LEAST SUGGESTED VALUE FIRST - A New Search Heuristic to Reduce the Amount of Backtracking Calls in CSP.

In Proceedings of the 2nd International Conference on Agents and Artiﬁcial Intelligence - Artiﬁcial Intelligence, pages 416-421

DOI: 10.5220/0002761504160421

 SciTePress

2 CSP AND HEURISTICS

In this section, we introduce the basic concepts of

CSP and further, we detail the most common

heuristics used for this kind of problem.

2.1 Constraint Satisfaction Problems

Roughly speaking, CSP are problems defined by a

set of variables X = {X

, X

,…, X

}, where each one

) ranges in a known Domain (D), and a set of

Constraints C = {C

, C

,…, C

} which restricts

specifically one or a group of variables with the

values they can assume. A consistent complete

solution corresponds to a full variable valuation,

which is further in accordance with the constraints

imposed. Along the paper, we refer to the variables

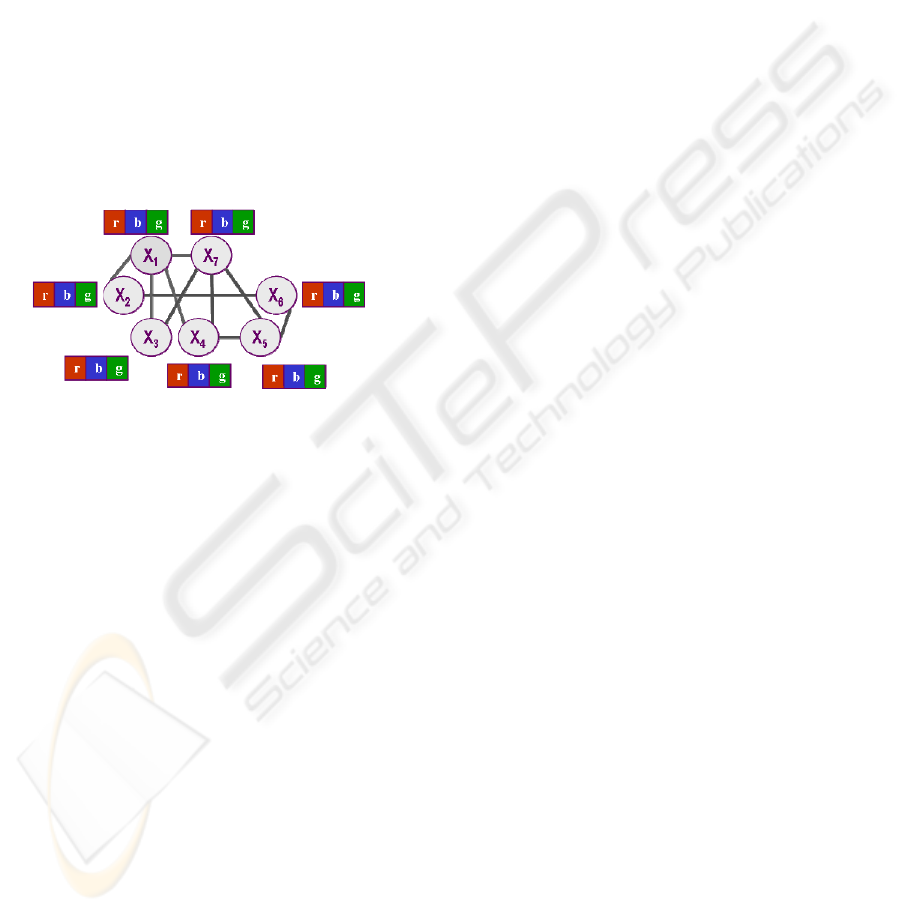
as entities. Figure 1 depicts a pedagogical problem.

Figure 1: A pedagogical Constraint Satisfaction Problem.

In the above figure, the entities are {X

, X

} and each one can assume one of the

following value: D = {r,g,b}, referring to the

colours, red, green, and blue, respectively. The only

constraint imposed restricts the neighbouring places

(that is, each pair of nodes linked by an arc) to have

different colours. As usual, this problem can be

reformulated into a search tree problem, where the

branches represent all the possible paths to a

consistent solution. By definition, each branch not in

accordance with C, must be pruned. The

backtracking algorithm, a special case of depth-first,

is neither complete nor optimal, in case of infinite

branches (Vilain et. al, 1989). As we have not

established an optimal solution to the problem, our

worries rely only upon the completeness of the

algorithm. However, we only take into account

problems in which search does not lead to infinite

branches, and thus, the completeness of the problem

is ensured.

2.2 Search Heuristics

Basically, the backtracking search is used for this

sort of problems. Roughly, in a depth-first manner, a

value from the domain is assigned, and whenever an

inconsistency is detected, the algorithm backtracks

to choose another colour (another resource).

Although simple in conception, the search results are

far to be satisfactory. Further, this algorithm lacks

for not being intelligent, in the sense to re-compute

partial valuations already prove to be consistent. A

blind search, like the backtracking, is improved in

efficiency employing some heuristics. Regarding

CSP, general heuristics (that is, problem-

independent, opposite to domain-specific heuristics,

as the ones in A* search (Dechter & Pearl, 1985))

methods speed up the search while removing some

sources of random choice, as:

 Which next unassigned variable should be

taken?

 Which next value should be assigned?

The answer for the questions above arises by a

variable and value ordering. The most famous

heuristics are highlighted below. Note that the two

first methods concern the variable choice, and the

later refers to the value ordering:

 Most Constrained Variable avoids useless

computations when an assignment will

eventually lead the search to an inconsistent

valuation. The idea is to try first the variables

more prone to error;

 When the later method is useless, the Degree

Heuristic serves as a tie-breaker, once it

calculates the degree (number of conflicts) of

each entity;

 The Least Constraining-Value, in turn, sorts

decreasingly the values in a domain respecting

how much the value conflicts with the related

entities (that is, the values less shared are tried

first).

As said before, we have restricted our scope of

research to the class of problems similar to the

family of the four color theorem, where the domain

is the same for each variable. In this sense, the LCV

heuristic is pointless since the “level” of

constraining for each value is the same. This

drawback force us to search alternatives for sort the

values of CSP in similar situations, but also

improving the efficiency. However, before to

present the solution, it is worth to explain why we

have used the logic constraint programming CHRv

to carry out the tests.

LSVF: LEAST SUGGESTED VALUE FIRST - A New Search Heuristic to Reduce the Amount of Backtracking Calls in

CSP

417

3 CHR

Constraint Handling Rules with Disjunction (CHR

)

(Abdennadher & Schütz, 1998) is a general

concurrent logic programming language, rule-based,

which have been adapted to a wide set of

applications as: constraint satisfaction (Wolf, 2005),

abduction (Gavanelli et. al, 2008), component-

development engineering (Fages et. al, 2008), and

son on. It is designed for creation of constraint

solvers.

CHR

is a fully accepted logic programming

language, since it subsumes the main types of

reasoning systems (

Frühwirth, 2008): the production

system, the term rewriting system, besides Prolog

rules. Additionally, the language is syntactically and

semantically well-defined (Abdennadher & Schütz,

1998).

Concerning the syntax, a CHR

program is a set of

rules defined as:

Rule_name@ Hk \ Hr <=> G | B.

Rule_name is the non-compulsory name of the rule.

The head is defined by the predicates represented by

Hk and Hr, with which an engine tries to match with

the constraints in the store. Further, G stands for the

set of guard predicates, that is, a condition imposed

to be verified to fire any rule. Finally, B is the

disjunctive body, corresponding to a set of

constraints added within the store, whenever the rule

fires. The logical conjunction and disjunction of

predicates are syntactically expressed by the

symbols ‘,’ and ‘;’, respectively. Logically, the

interpretation of the rule is as follows:

∀V

(G → ((Hk ∧ Hr) ↔ (∃V

B\GH

B ∧

Hk))), where V

= vars(G) ∪

vars(Hk) ∪ vars(Hr), V

B\GH

= vars(B)

\ V

For the sake of space, we ask the reader to check the

bibliography for further reference to the declarative

semantics.

The problem depicted in figure 1 is represented

by the logical conjunction of the following rules:

f@ facts==> m, d(x1,C1), d(x7,C7),

d(x4,C4), d(x3,C3), d(x2,C2),

d(x5,C5), d(x6,C6).

d1@ d(x1,C) ==>

C=red;C=green;C=blue.

d7@ d(x7,C) ==>

C=red;C=green;C=blue.

d4@ d(x4,C) ==>

C=red;C=green;C=blue.

d3@ d(x3,C) ==>

C=red;C=green;C=blue.

d2@ d(x2,C) ==>

C=red;C=green;C=blue.

d5@ d(x5,C) ==>

C=red;C=green;C=blue.

d6@ d(x6,C) ==>

C=red;C=green;C=blue.

m@ m <=> n(x1,x2), n(x1,x3),

n(x1,x4), n(x1,x7), n(x2,x6),

n(x3,x7), n(x4,x7), n(x4,x5),

n(x5,x7), n(x5,x6).

n1@ n(Ri,Rj), d(Ri,Ci), d(Rj,Cj)<=>

Ci=Cj | fail.

The first rule ‘f’ introduces the constraints into

the store, which is a set of predicates with functor d

and two arguments: the entity and a variable to store

the valuation of the entity. The seven following rules

relate the entity with the respective domain.

Additionally, rule ‘m’ adds all the conceptual

constraints, in the following sense: n(Ri,Rj) means

there is an arc linking Ri to Rj, thus, both entities

could not share the same color. Finally, the last rule

is a sort of integrity constraint. It fires whenever the

constraints imposed is violated. Logically, it says

that if two linked entities n(Ri,Rj) shares the same

color (condition ensured by the guard), then the

engine needs to backtrack to a new (consistent)

valuation.

In the literature, many operational semantics was

proposed, as (Abdennadher et. al, 1999). However,

the ones most used in CHR

implementations are

based on the refined semantics (Duck et. al, 2004)

(as the SWI-Prolog version 5.6.52 (SWI-Prolog,

2008) used in the examples carried out along this

paper). According the refined operational semantics,

when more than one rule is possible to fire, it takes

into account the order in which the rules were

written in a program. Hence, as SHD heuristic

orders the entities to be valued in accordance with

the level of constraining, this pre-analysis help us to

write the rules based on this sort. Thus, we could

concentrate our effort on the order of the values in

the domain.

4 LEAST SUGGESTED VALUE

FIRST - LSVF

The last section has introduces the rule-based

constraint language, CHR

. Many aspects of the

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

418

operational semantics were left unexplained, and we

encourage the reader to check the references for

additional information. However, some points need

be discussed to clarify the technique developed to

improve the search, decreasing the amount of

backtracking calls. The first point, “which rule will

trigger”, was discussed before. The second

important subject of discussion is the order of which

the values are taken from the domain in the search.

We have already said that the logical disjunction is

denoted in the body of a CHR

rule, syntactically

expressed by ‘;’. In order to maintain consistency

with the declarative semantics, CHR

engine tries all

the alternatives since the user tell the engine to do

so. A disjunctive body is always evaluated from left-

to-right.

d1@ d(x1,C) ==>

C=red;C=green;C=blue.

Taking a rule from the example (as stated

above), the engine tries the following order of

valuation for X1: (1) red, (2) green and, (3) blue. All

the rules were created respecting the same valuation

order.

At first glance, we can note a relevant problem:

if all the entities try first the same colour, and we

know that these entities are related, a second

evaluated entity always needs to backtrack.

Furthermore, since the entities shares the same

domain, LCV is pointless: each value has the same

level of constraining. In order to make our idea

clear, we introduce a second example.

Figure 2: An example regarding the order of the colours.

The Figure 2 shows the motivation problem for the

new heuristics discussed. There are 3 entities

}, each one sharing the same domain. Let

us respect the order of valuation from left to right,

and the order of variable chosen based on the

numerical order. Thus, the engine works as follows:

I. X

is chosen, and the colour red is taken;

II. X

is chosen, and the colour red is taken;

III. Inconsistency found: backtracking;

IV. X

is chosen, and the colour blue is taken;

V. X

is chosen, and the colour red is taken;

VI. Inconsistency found: backtracking;

VII. X

is chosen, and the colour blue is taken;

VIII. Inconsistency found: backtracking;

IX. X

is chosen, and the green is taken.

Following, in the Figure 3, the values order is

changed to avoid, as much as possible, the conflicts.

Figure 3: The same example with values re-ordered.

The engine now works as stated below:

I. X

is chosen, and the colour red is taken;

II. X

is chosen, and the colour blue is taken;

III. X

is chosen, and the colour green is taken.

The above modification prevented the backtracking

calls, and the solution was reached just with three

steps, unlike the last example, which did the same,

in 9 steps. Evidently, in practice, we can not avoid

all backtracking calls, but each reduction is well-

suited for the overall search time-consumption.

4.1 How the Heuristic Works?

Our propose is to enjoy the operational semantics

addressed by the CHR

implementation to sort the

order in which the values from the domain is

asserted, removing the amount of backtracking calls.

We believe this reduction can be well appreciated in

large and complex problems, where the time is a

relevant factor.

The approach does not yield only the first colour,

but the entire domain. In our case, the focus is in

problems with three or four colours. In this context,

the members of the set of entities are categorized in

accordance with the level of corresponding

restriction:

 Soft Entities, that is, less constrained;

 Middle Entities, that is, half constrained;

 Hard Entities, that is, more constrained.

Hence, instead of proposing a solution of

random sorting, we have taken the following

assumptions:

 Usually, the entities less constrained are likely

linked to others more constrained, and, further,

the entities less restricted are not connected to

LSVF: LEAST SUGGESTED VALUE FIRST - A New Search Heuristic to Reduce the Amount of Backtracking Calls in

CSP

419

each other (if this were the case, the entities

owned other restrictions than those that connect

them, and they would be deemed more

constrained). Thus, the domain of these entities

are sorted in the same manner;

 Normally, hard entities are linked to middle

ones, and thus the order of valuation must be in

conformance to this fact, example, if a hard

entities domain is ordered like (1)red, (2)green,

(3)blue, the middle should be sorted like

(1)blue, (2) green (3)red, that is, the less

suggested values first.

 The first value assumed by the hard entities

should be the last for the soft and middle

entities, since potentially both are linked to the

former (this is why they were classified as

hard).

In order to exemplify this approach, we are

going to show the reformulation of the example used

along this paper, illustrating gradually the gains

obtained.

With respect the problem, we divided the set of

entities as follows: (i) soft entities: {X

}, (ii)

middle entities: {X

}, and (iii) hard entities

}, with 6, 9 and 12 conflicts, respectively.

What was considered for division was precisely the

amount of conflict in relation to other variables,

done according the Static Highest Degree (SHD)

heuristic.

Table 1 summarizes the amount of inferences

made and the number of backtracking calls. The

time is a relevant aspect only when evaluated to

large problems.

Table 1: First Results with the LSVF Heuristic.

Sorting Level Inferences Backtracking Calls

I 4,897 8

II 4,694 7

III 4,415 6

IV 4,208 5

Not accidentally, the table was populated according

to the level of values sorted in respect to the

assumptions raised earlier. Each level corresponds to

a different CHR

program.The Sorting Levels are

the following:

Table 2: Domain Used for the Entities.

Level Soft Middle Hard

I red, green blue red, green blue red, green blue

II red, green blue blue, red, green red, green blue

III green, red blue blue, red, green red, green blue

IV green, blue, red blue, green, red red, green blue

In the Level I, the heuristic was not used. It is

worth to keep their results in the table to compare

with the other levels, where the assumptions (which

define the LSVF) were gradually applied. Level II

has changed the first suggested colour of the Middle

entities with respect the hard. Following, the level

III has changed the first colour of domain of soft

entities with respect the others (middle and hard).

There has been a reduction of 25% of backtrack calls

in accordance with the level I. Finally, the level IV

has used all assumptions talked, and both measures

were visibly reduced. In this latter case, the engine

backtracks 5 times, three calls less than the original

program. Note that level IV obeys all the

assumptions discussed, and the results obtained were

remarkable.

5 FINAL REMAKES’ AND

FUTURE WORK

The preliminary results obtained were very

satisfactory. We might see that, as we organize the

values of the domain of the entities, gradually the

search has been getting more efficient with respect

to the number of inferences necessary to reach a

solution. A small comparison between the level I

and level IV, the program without the heuristic and

the program totally in accordance with LSVF,

respectively, shows a significant reduction in the

amount of backtrackings and inferences realized.

It was important to mention that we are neither

worried with optimal solutions nor with all the

solutions for the problem. We only focus on our

overall effort to reach a solution, and nothing else.

In order to validate completely the LSVF

heuristics, our next step is to analyse the approach

with more complex problems. Additionally, our aim

is to check the time resource allocated for this kind

of problem, since this was not possible due to the

size of the example discussed (all instances executed

in less than one second).

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

420

ACKNOWLEDGEMENTS

We acknowledge REUNI for financial support and

the Center of Informatics of Federal University of

Pernambuco – CIn/UFPE – Brazil for support in this

research.

REFERENCES

Abdennadher, S., and Schütz, H., 1998. CHRv: A Flexible

Query Language, In Proceedings of the Third

International Conference on Flexible Query

Answering Systems, p.1-14, May 13-15.

Abdennadher, S., Frühwirth, T., and Meuss, H. 1999.

Confluence and Semantics of Constraint Simplification

Rules.Constraints 4, 2 (May. 1999), 133-165.

Brailsford, S., Potts, C., and Smith, B. 1999. Constraint

satisfaction problems: Algorithms and applications.

European J. Operat. Res. 119, 557--581.

Dechter, R. and Pearl, J. 1985. Generalized best-first

search strategies and the optimality of A*. J. ACM 32,

3 (Jul. 1985), 505-536.

Duck, G. J., Stuckey, P. J., De la Banda, M. G. and

Holzbaur, C. 2004. The Refined Operational

Semantics of Constraint Handling Rules. In

Proceedings of the 20th International Conference on

Logic Programming, B. Demoen and V. Lifschitz,

Eds., 90-104.

Fages, F., Rodrigues, C. M. O., and Martinez, T.

2008. Modular CHR with ask and tell. In T.

Schrijvers, F. Raiser, and T. Frühwirth, editors, CHR

'08: Proc. 5th Workshop on Constraint Handling

Rules, Hagenberg, Austria, pages 95-110, 2008. RISC

Report Series 08-10, University of Linz, Austria.

Frühwirth, T. 2008. Welcome to Constraint Handling

Rules. In Constraint Handling Rules: Current

Research Topics, T. Schrijvers and T. Frühwirth, Eds.

Lecture Notes In Artificial Intelligence, vol. 5388.

Springer-Verlag, Berlin, Heidelberg, 1--15.

Gavanelli, M., Alberti, M., and Lamma, E. 2008.

Integrating Abduction and Constraint Optimization in

Constraint Handling Rules. In Proceeding of the 2008

Conference on ECAI 2008: 18th European Conference

on Artificial intelligence. M. Ghallab, C. D.

Spyropoulos, N. Fakotakis, and N. Avouris, Eds.

Frontiers in Artificial Intelligence and Applications,

vol. 178. IOS Press, Amsterdam, The Netherlands,

903-904.

Robertson, N., Sanders, D. P., Seymour, P. D., and

Thomas, R., 1997. The four colour theorem, J.

Combin. Theory Ser. B., 2--44.

Russel, S., Norvig, P., 2003 The book, Artificial

Intelligence: A Modern Approach. New Jersey:

Prentice-Hall, 2

edition, 143--144.

SWI-Prolog. 2008. Reference Manual. Avaliable in

http://gollem.science.uva.nl/SWI-Prolog/Manual/

Contents.html. Last access in 15th September 2009.

Vilain, M., Kautz, H. and Beek, P. van. 1989. Constraint

propagation algorithms for temporal reasoning: A

revised report. In D. S. Weld and J. de Kleer,

editors, Readings in Qualitative Reasoning about

Physical Systems, pages 373-381. Morgan Kaufmann.

Wolf, A. 2005. Intelligent search strategies based on

adaptive Constraint Handling Rules. Theory Pract.

Log. Program. 5, 4-5 (Jul. 2005), 567-594.

LSVF: LEAST SUGGESTED VALUE FIRST - A New Search Heuristic to Reduce the Amount of Backtracking Calls in

CSP

421