SOUND SUMMARIZATIONS FOR ALC H I ONTOLOGIES

How to Speedup Instance Checking and Instance Retrieval

Sebastian Wandelt and Ralf M

oller

Institute for Software Systems, Hamburg University of Technology, Schwarzenbergstrae 95, Hamburg, Germany

Keywords:

Description logics, Ontologies, Reasoning, Scalability.

Abstract:

In the last years, the vision of the Semantic Web fostered the interest in reasoning over ever larger sets of

assertional statements in ontologies. In this senario, state-of-the-art description logic reasoning systems cannot

deal with real-world ontologies any longer, since they rely on in-memory structures.

In these scenarios it will become more important to rely on unsound or incomplete reasoning structures, to

obtain a set of candidates/obvious solutions to queries, i.e. only apply state-of-the-art reasoning systems to the

computationally hard solutions. In this paper we propose a summarization-based approach which is always

sound, but possibly incomplete. We think that this technique will support description logic systems to deal

with the steadily growing amounts of assertional data.

1 INTRODUCTION

As the Semantic Web evolves, scalability of inference

techniques becomes increasingly important. Even for

basic description logic-based inference techniques,

e.g. concept satisﬁability, it is only recently under-

stood on how to perform reasoning on large ABoxes

in an efﬁcient way. This is not yet the case for prob-

lems that are too large to ﬁt into main memory. In this

paper we present an approach to optimize instance re-

trieval tests on ontologies, by summarization of sim-

ilar individuals in the assertional part of an ontology.

The general picture is as follows:

• Keep a sound, but possibly incomplete data-

structure, called Summarization, in main memory

• On incoming queries, consult the summarization

ﬁrst to obtain a list of candidate solutions/obvious

answers

• For all left-over potential answers, compute the

outcome with a description logic reasoner, e.g. in

our case Racer(Haarslev and M

oller, 2001)

The remaining part of the paper is structured as fol-

lows. Section 2 provides the formal background for

description logics, presents some related work and

introduces an example ontology, which will be used

throughout the paper. In Section 3 and 4, we present

our data-structure for sound, and possibly incomplete

reasoning. How to use these results for description

logic reasoning is shown in 5. In Section 6 we present

preliminary evaluation of the proposed algorithm with

respect to a benchmark ontology. We conclude with

Section 7.

2 FOUNDATIONS

2.1 Description Logics

We brieﬂy recall syntax and semantics of the descrip-

tion logic ALC H I . For the details about the descrip-

tion logic ALC H I , please refer to (Baader et al.,

2007). We assume a collection of disjoint sets: a set

of concept names N

, a set of role names N

and

a set of individual names N

. The set of roles N

∪ {R

−

|R ∈ N

}. We say that a concept descrip-

tion is atomic, if it is a concept name. With N

we de-

note all atomic concepts. For deﬁning the semantics

see (Baader et al., 2007). Furthermore we assume the

notions of TBoxes (T ), RBoxes (R ) and ABoxes (A)

as in (Baader et al., 2007). With ASSERT IONS(A)

we denote the set of assertions in an ABox A and with

we denote the set of all ABoxes.

A ontology O consists of a 3-tuple hT , R , Ai,

where T is a TBox, R is a RBox and A is a ABox.

We restrict the concept assertions in A in such a

656

Wandelt S. and Möller R. (2010).

SOUND SUMMARIZATIONS FOR ALCHI ONTOLOGIES - How to Speedup Instance Checking and Instance Retrieval.

In Proceedings of the 2nd International Conference on Agents and Artiﬁcial Intelligence - Artiﬁcial Intelligence, pages 656-661

DOI: 10.5220/0002762206560661

 SciTePress

Figure 1: Guiding Example: ABox A

for ontology O

way that each concept description is an atomic con-

cept or a negated atomic concept. This is a com-

mon assumption, e.g. in (Guo and Heﬂin, 2006),

when dealing with large assertional datasets in on-

tologies. With Ind(A) we denote the set of in-

dividuals occurring in A. The set of equivalence

classes of an equivalence relation Rel is denoted

[Rel]. When deﬁning an equivalence relation, we will

sometimes use the following syntax for convenience:

R = {(a, b, c, d), (e, f ), (g, h, i)}. The meaning is, that

a, b, c, d are equivalent, e and f are equivalent, and

g, h, i are equivalent w.r.t. R. The expression ran( f )

denotes the range of a function f . Whenever we have

a pair p = hA, Bi, we access the elements by a dot-

operator, e.g. p.A.

2.2 Related Work

Recently, an approach for partitioning large OWL

ontologies has been presented in (Guo and Heﬂin,

2006). The idea is to partition a large ABox into

smaller ABoxes, s.t. reasoning on the smaller asser-

tional subsets is complete, but possibly unsound. Al-

though the authors report impressive results for the

increase in performance, we see some issues as iden-

tiﬁed (Wandelt, 2008). In (Fokoue et al., 2006), the

authors propose a method to reduce the number of in-

dividuals in an ABox for complete but unsound rea-

soning. Afterwards, a ﬁltering algorithm is applied

to obtain soundness again. This ﬁlter-step is usually

quite sophisticated and time-consuming. In a similar

way as the partitioning-approach given in (Guo and

Heﬂin, 2006), a Summary ABox has to be build in

a precomputation step, which depends on the actual

and complete ABox. Thus, the approach is not per-

se applicable to updateable ontologies. After all, our

work can be seen as complementary to other work.

For more information refer to Section 6.

2.3 Guiding Example

In the following we deﬁne an example ontology,

which is used throughout the remaining part of the pa-

per. The ontology is inspired by LUBM (Guo et al.,

2005), a benchmark-ontology in the setting of univer-

sities. Although this is a synthetic benchmark, sev-

eral (if not most) papers on scalability of ontological

reasoning consider it as a base reference. We take a

particular a snapshot from the LUBM-ontology (Ex-

ample 1) to make our approach more visible and clear.

We evaluate our ideas w.r.t. to “full” LUBM in Sec-

tion 6.

Example 1. Let O

= hT

, R

, A

i, s.t.

={Chair ≡ ∃headO f .Department u Person, Pro f v Person

Graduate v Student, Student ≡ Person u ∃takes.Course}

={headO f v worksFor}

=see Figure 1

3 ABOX SUMMARIZATIONS

Deﬁnition 1. Let N

sum

be a set of summarization in-

dividuals, then a ABox-Summarization (for an ABox

A) is a pair AS = hφ

sum

, ω

sum

i, s.t.

• φ

sum

is a total function Ind(A) → N

sum

and

• ω

sum

is a total function N

sum

→ S

The intuition of Deﬁnition 1 is that φ

sum

maps each

named individual in the source ABox A to a sum-

marization individual, and ω

sum

determines a set of

ABox-assertions for each such summarization indi-

vidual.

Example 2. Example for ABox-Summarization

EX1

w.r.t. A

sum

={s, c, p}

sum

= {( joe, s), (laura, s), (alice, s),

(luis, s), (anna, s), (cl, c),

(ai, c), (ai2, c), (tl, c), (amanda, p),

( f rank, p), ( jim, p), (in f , p)}

sum

= {(s, {Student(s), takes(s, e), Course(e)}),

(c, {Course(c)}),

(p, {Pro f (p)})}

SOUND SUMMARIZATIONS FOR ALCHI ONTOLOGIES - How to Speedup Instance Checking and Instance Retrieval

657

Please note that the ABoxes ω

sum

might introduce

new individual names, e.g. the name e here.

We will deﬁne φ

sum

usually by use of an equivalence

relation R

sum

, where N

sum

(the range of φ

sum

) is as-

sumed the set of equivalence classes in R

sum

, i.e.

sum

]. The correspondence between both notions is

as deﬁned follows:

sum

(a) = φ

sum

(b) ⇐⇒ R

sum

(a, b)

Example 3. An example equivalence relation

sum

for φ

sum

could be:

sum

= {( joe, laura), (laura, joe),

(laura, alice), (alice, laura),

( joe, alice), (alice, joe),

( f rank, jim), ( jim, f rank),

( f rank, f rank)}

Let us relate ABox-Summarizations to description

logic reasoning. Therefore, we can distinguish two

properties: soundness and completeness with respect

to description logic inferences.

Deﬁnition 2. An ABox-Summarization (for an ABox

A) is sound, if we have that

hT , R , ω

sum

(φ

sum

(a))i  C(φ

sum

(a)) =⇒

hT , R , Ai  C(a).

Deﬁnition 3. A ABox-Summarization (for an ABox

A) is complete, if we have that

hT , R , Ai  C(a) =⇒

hT , R , ω

sum

(φ

sum

(a))i  C(φ

sum

(a)).

Both properties can be used to assess the quality

of an ABox-Summarization, i.e. if you have nei-

ther soundness nor completeness, then the ABox-

Summarization is usually not of use for descrip-

tion logic inferences. To further evaluate ABox-

Summarizations, we introduce the notion of ”‘am-

icability”’, which estimates how much the ABox-

Summarization can speed up solving description logic

decision problems.

Deﬁnition 4. The amicability of an ABox-

Summarization AS = hφ

sum

, ω

sum

i (for an ABox

A) is deﬁned as

amic(AS) = −log

(

ran(φ

sum

)

|Ind(A)|

)

Example 4. An Example ABox-Summarization

EX2

, which is trivially sound and complete, is

• N

sum

= Ind(A

)

• R

sum

= {(x, x)|x ∈ Ind(A

)}

• ω

sum

(x) = A

, for all x ∈ Ind(A

)

In the example above, we do not merge any two indi-

viduals, and for reasoning over each individual we use

the whole ABox. As one can see from amic(AS

EX1

) =

0, this trivial ”‘summarization”’ will not yield any im-

provement for reasoning over individuals.

4 SOUND SUMMARIZATION

In the following we discuss a non-trivial summariza-

tion, which always enables sound reasoning, and in

some cases even complete reasoning; with a quite en-

couraging amicability. To deﬁne the summarizations,

we ﬁrst look at which individuals we want to merge.

Our general intuition is, informally, that similar indi-

viduals should behave equally during reasoning. Thus

we will deﬁne some notions to talk about similarity of

two individuals in an ABox A.

Deﬁnition 5. An Anonymous Node Successor (ANS)

of an individual a for an ABox A is a pair ANS

hrs, csi, s.t. ∃b ∈ Ind(A) with

1. ∀R ∈ rs.(R(a, b) ∈ A ∨ R

−

(b, a) ∈ A)

2. ∀C ∈ cs.C(b) ∈ A

3. cs and rs are maximal

The third criteria (maximality) is important for cases,

when two individuals can be connected by more than

one role assertion.

Example 5. An example for two anonymous node

successors of f rank are:

• ANS1

f rank

= h{teaches}, {Course}i

• ANS2

f rank

= h{headO f }, {Department}i

Next, we combine all anonymous node successors

of an individual a in an ABox A and add the directly

asserted concepts of a, to create a summarization rep-

resentative, called One Step Node.

Deﬁnition 6. A One Step Node of an individual a for

an ABox A is a pair OSN

= hrootconset, ansseti, s.t.

• rootconset = {C|a : C ∈ A} and

• ansset is the set of all Anonymous Node Succes-

sors of individual a

Example 6. We have

OSN

f rank

= h{Pro f }, {h{teaches}, {Course}i,

h{headO f }, {Department}i}i

We use One Step Nodes to deﬁne a similarity relation

among individuals in an ABox A.

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

658

Deﬁnition 7. Two individuals a and b are called One

Step Node-similar for an ABox A, if we have OSN

OSN

. We denote the One Step Node-similarity rela-

tion for an ABox A with R

OSNSim

And last but not least, we deﬁne the notion of an OSN-

based ABox-Summarization.

Deﬁnition 8. An ABox-OSN-Summarization (for

an ABox A and an One Step Node-similarity rela-

tion R

OSNSim

) is an ABox-Summarization AOSNS

hφ

sum

, ω

sum

i, s.t.

• N

sum

=[R

OSNSim

]

• We deﬁne φ

sum

by the equivalence relation

OSNSim

• For each osn ∈ [R

OSNSim

]

sum

(osn) ={C(osn

∗

)|C ∈ osn.rootconset}∪

[

ans∈osn.ansset

{R(a, ans

∗

)|R ∈ ans.rs}∪

[

ans∈osn.ansset

{C(ans

∗

)|C ∈ ans.cs}

, where x

∗

denotes a fresh and unique individual name

for each OSN-/ANS-object x.

Example 7. One ABox-OSN-Summarization AS

EX 3

for A

and R

sum

EX 3

= {( joe, lara, alice, luis),

(cl, ai, ai2), (tl), (ana), (amanda), ( f rank), ( jim), (in f )} is

sum

EX 3

={s1, s2, c1, c2, p1, p2, p3, d1}

sum

( joe) = s1

sum

(lara) = s1

sum

(cl) = c1

sum

(in f ) = d1

sum

EX 3

(s1) = {Student(s1), takes(s1, cnew1),

Course(cnew1)}

sum

EX 3

(s2) = {GradStudent(s2), takes(s2, cnew2),

Course(cnew2)}

sum

EX 3

(p2) = {Pro f (p2), teaches(p2, cnew5),

Course(cnew5), headO f (p2, newd1),

Department(newd1)}

5 HOW TO SOLVE DECISION

PROBLEMS?

The main theorem of our work is presented in Theo-

rem 5.1.

Theorem 5.1. Given an Ontology hT , R , Ai, every

ABox-OSN-Summarization AOSNS

for A is sound.

This is, informally, clear, since the ABox of each

summarization individual is a subset of the original

ABox A (modulo renaming).

Proof. We have to show that hT , R , ω

sum

(φ

sum

(a))i 

C(φ

sum

(a)) =⇒ hT , R , Ai  C(a).

We show the proof by contraposition and then

derive a contradiction: Given hT , R , Ai 2 C(a), we

have that there exists a model I

for hT , R , A ∪

{¬C(a)}i. Now, I

has to satisfy all the asser-

tions in A ∪ {¬C(a)}, and since ω

sum

(φ

sum

(a)) ∪

{¬C(φ

sum

(a))} is structurally equivalent (by con-

struction in Deﬁnitions 5, 6 and 8) to a subset of A ∪

{¬C(a)}, we have that a rewriting of I

has to satisfy

all the assertions in ω

sum

(φ

sum

(a)) ∪ {¬C(φ

sum

(a))}.

Thus, there exists a model for hT , R , ω

sum

(φ

sum

(a))∪

{¬C(φ

sum

(a))}i. Contradiction, since we assumed

hT , R , ω

sum

(φ

sum

(a))i 2 C(φ

sum

(a)) (by Contraposi-

tion).

Given Theorem 5.1 above, we can speedup query an-

swering over description logics in the following ways.

Given an individual a and an atomic concept de-

scription C, Instance Checking is the problem to de-

termine, whether an Ontology hT , R , Ai  C(a). In

common description logic systems, this is done by

checking, whether hT , R , A ∪ {¬C(a)}i is inconsis-

tent. Once the ABox is reasonably big, the underlying

exponential behavior of tableau algorithms shows up

easily, albeit all known optimizations techniques.

Given an ABox-OSN-Summarization AOSNS

for A, we can perform some kind of sanity check with

existing tableau algorithms, but dramatically reduced

ABoxes.

1. Check, whether hT , R , ω

sum

(φ

sum

(a))i 2

C(φ

sum

(a)). If this is true, then we already

know that hT , R , Ai  C(a).

2. Check, whether hT , R , ω

sum

(φ

sum

(a))i 2

¬C(φ

sum

(a)). If this is true, than we already

know that hT , R , Ai  ¬C(a), and it is safe to

assume that hT , R , Ai 2 C(a) (if the underlying

ontology is consistent).

Please note that we deal with a dramatically reduced

assertional part in both cases. Only if both sanity

checks fail, then we still have to apply the full reason-

ing machine, i.e. we have to check hT , R , Ai  C(a).

The main contribution of this work is the speedup

of Instance Retrieval. Given an atomic concept de-

scription C, Grounded Instance Retrieval is the prob-

lem to determine all individuals a ∈ A, s.t. we have

hT , R , Ai  C(a).

SOUND SUMMARIZATIONS FOR ALCHI ONTOLOGIES - How to Speedup Instance Checking and Instance Retrieval

659

Given an ABox-OSN-Summarization AOSNS

for A, we can obtain a sound result set as follows:

1. SoundResult =

2. For all s ∈ N

sum

• If hT , R , ω

sum

(s)i  C(s), then SoundResult =

SoundResult ∪φ

−

sum

(a)

Informally, we iterate over all summarization individ-

uals s ∈ N

sum

and check, whether they are instances of

concept description C. If yes, then we add all individ-

uals represented by that summarization individual to

the set of sound answers.

6 IMPLEMENTATION AND

EVALUATION

We implemented our proposal in Java with the help

of OWLAPI(Bechhofer et al., 2003) and investigated

several criteria for evaluation w.r.t. to the Lehigh Uni-

versity Benchmark with up to 1000 universities. Each

university in the benchmark has around 20 associated

departments. Please note that we have implemented

all data structures in an updateable way. This is im-

portant when one deals with constantly changing in-

formation, e.g. in streams of information. To the best

of our knowledge, other related work does not yet dis-

cuss updateable information yet.

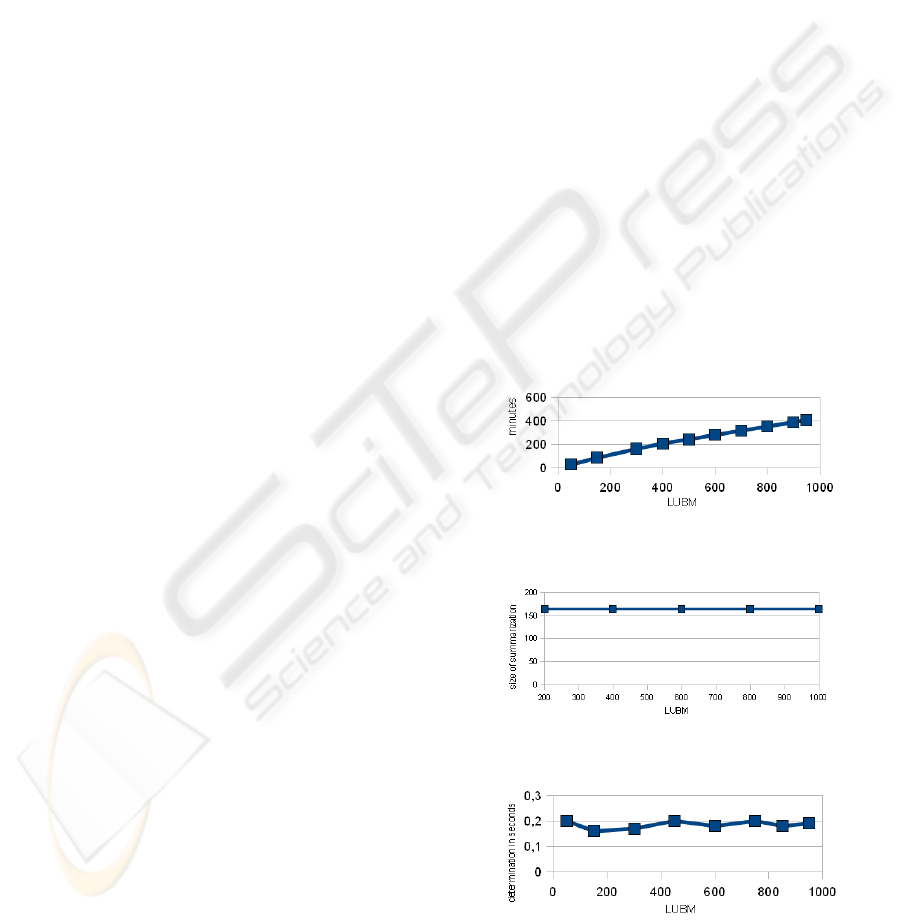
1. Figure 2 shows the time needed to create ABox-

OSN-Summarizations for a given number of uni-

versities. It is worth to notice that the loading time

exhibits linear-time behavior, which corresponds

to the size of the input data. When breaking down

the loading time to triples, we are able to load

around 4000 Triples/second in average.

2. Number of summarization individuals Figure 4

shows the size of N

sum

, i.e. the number of summa-

rization individuals in the corresponding ABox-

OSN-Summarization. The number of individuals

remains constant over time. Only during load-

ing the ﬁrst universities, the size grows, until the

Summarization becomes saturated, i.e. no more

new One Step Nodes are created, but only already

known One Step Nodes used. The constant num-

ber enables constant-time sound instance retrieval

in case of LUBM.

3. Time for Sound Instance Retrieval We performed

Grounded Instance Retrieval for the concept de-

scription Chair over LUBM. As expected, the

time for sound instance retrieval, shown in Fig-

ure 4, is constant as well (the number of Sum-

marization Individuals does not change). Please

note that Figure 4 only shows the time for real

reasoning over the corresponding ABox-OSN-

Summarization with Racer.

Separately, we show the time necessary to look up

the individual names for the summarization indi-

viduals in Figure 5. It is easy to see that, while

the reasoning itself is constant, the lookup time

grows linear. The reason is that the number of

Chair-instances grows linearly as well, as shown

in Figure 6. E.g. in LUBM with 1000 universities,

we have already around 20000 Chair-instances.

4. Amicability Finally, we show the amicability of

the corresponding ABox-OSN-Summarization in

Figure 7.

5. Completeness It is interesting to notice that our

further analysis showed that all ABox-OSN-

Summarization for LUBM turned out to be not

only sound, but also complete. That means, we

have constant time grounded instance retrieval for

LUBM. The reason is that most of the termino-

logical axioms in LUBM are rather domain/range-

constraints, which are completely covered by our

One Step Nodes. We did not have time to ﬁnish

these investigations, but the results look quite en-

couraging so far.

Figure 2: Loading time.

Figure 3: Size of N

sum

Figure 4: Reasoning over summarization individuals - solu-

tion determination.

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

660

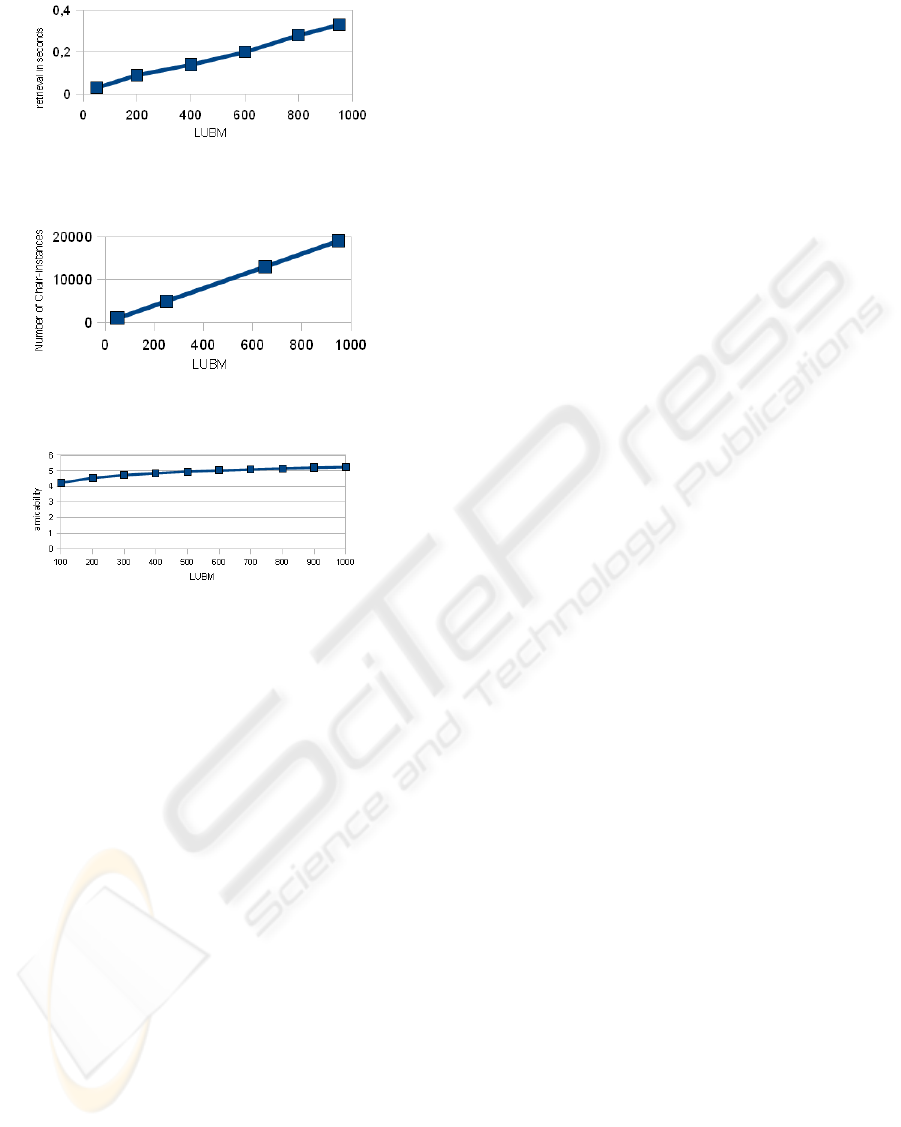
Figure 5: Reasoning over summarization individuals - look

up.

Figure 6: Number of Chair instances.

Figure 7: Amicability.

7 CONCLUSIONS AND FUTURE

WORK

We have proposed a method for sound instance re-

trieval over ontologies. Our idea for summarization

of individuals is not completely new, but to the best of

our knowledge we are the ﬁrst to propose sound rea-

soning over individuals based on similarity. The re-

sults are encouraging so far, especially in combination

with the recently discovered completeness-property

for LUBM. Even though other real-world ontologies

might not share the completeness-property, it seems

likely, that large subsets of these ontologies are still

domain-/range-constraints, and thus easily covered

by ABox-OSN-Summarizations. It was furthermore

shown that the approach has potential to deal with up-

dateable information.

For Future Work, we plan to further investigate the

completeness of ABox-OSN-Summarizations. Fur-

thermore it will be important to investigate more on-

tologies and check the performance of our proposal.

In the end, LUBM is only a synthetic benchmark cre-

ated to score description logic reasoning systems. But

whether it will perform in real-world scenarios is still

vague. Finally, we want to extend our proposal to

more expressive description logics, e.g. SHIQ or even

SHOIQ. While the extension is easy w.r.t. soundness,

completeness testing seems to be the harder problem.

REFERENCES

Baader, F., Calvanese, D., McGuinness, D. L., Nardi, D.,

and Patel-Schneider, P. F. (2007). The Description

Logic Handbook. Cambridge University Press, New

York, NY, USA.

Bechhofer, S., Volz, R., and Lord, P. (2003). Cooking the

Semantic Web with the OWL API.

Fokoue, A., Kershenbaum, A., Ma, L., Patel, C., Schonberg,

E., and Srinivas, K. (2006). Using Abstract Evalua-

tion in ABox Reasoning. In SSWS 2006, pages 61–74,

Athens, GA, USA.

Guo, Y. and Heﬂin, J. (2006). A Scalable Approach for

Partitioning OWL Knowledge Bases. In SSWS 2006,

Athens, GA, USA.

Guo, Y., Pan, Z., and Heﬂin, J. (2005). Lubm: A benchmark

for owl knowledge base systems. J. Web Sem., 3(2-

3):158–182.

Haarslev, V. and M

oller, R. (2001). Description of the

RACER System and its Applications. In Proceedings

International Workshop on Description Logics (DL-

2001), Stanford, USA, 1.-3. August, pages 131–141.

Wandelt, S. (2008). Partitioning owl knowledge bases - re-

visited and revised. In Description Logics.

SOUND SUMMARIZATIONS FOR ALCHI ONTOLOGIES - How to Speedup Instance Checking and Instance Retrieval

661