
A COMPARISON OF FOUR UNSUPERVISED CLUSTERING
ALGORITHMS FOR SEGMENTING BRAIN TISSUE IN
MULTI-SPECTRAL MR DATA
Maria C. Vald
´
es Hern
´
andez, J. M. Wardlaw
SFC Brain Imaging Research Centre, Division of Clinical Neurosciences, University of Edinburgh
Western General Hospital, Crewe Road, Edinburgh, Scotland
Sean Murphy
Institute for System Level Integration, Alba Campus, Livingston, Scotland
Keywords:
Unsupervised clustering, Segmentation, Multi-spectral MR, KMeans, EM, MeanShift, MVQ, Brain tissue,
Grey matter, White matter, CSF.
Abstract:
The effects of atrophy and diffusion of the boundary between grey and white matter, common in elder individ-
uals, represents a difficult problem for segmentation, not observed in healthy younger adults. The aim of this
study is to evaluate four well-known unsupervised clustering algorithms in brain tissue segmentation using
MR scans with atrophies and lesions. The brain is segmented into 3 different types: white matter, grey matter
and CSF. We used four MR sequences: T1W, T2W, T2
∗
W and FLAIR to classify each voxel in the image. No
spatial information was used. The algorithms tested were k−means, EM (Gaussian mixture), MVQ (minimum
variance quantisation) and Mean Shift. The datasets were acquired from an aged cohort (> 70 years). The
resulting segmentations were quantitatively compared to expertly collected ground truth on 12 datasets, using
the Dice coefficient as an overlap measure. The classification algorithms could be ranked in the following
order: MVQ, k−means, EM and MeanShift from best to worst. The MVQ algorithm did best of all with over
a .9 Dice overlap on CSF, and over .8 on white matter.
1 INTRODUCTION
Regional cerebral atrophy is a well known feature of
neurodegenerative diseases such as Alzheimer’s dis-
ease. Quantitative measures of regional atrophy based
on volume can serve as an aid to diagnosis for the neu-
rologist for such diseases although presently these ap-
proaches are not suitable for routine clinical diagno-
sis (Head et al., 2005; Lehtovirta et al., 1995; Busatto
et al., 2003; Good et al., 2001; Miller et al., 1980;
Burton et al., 2002).
Previous automated techniques typically involve
generating a binary mask of the tissue types in-
volved (normally white matter, grey matter and cere-
bral spinal fluid), e.g. (Crum, 2007), but can also gen-
erate an estimate of the fraction of each tissue in every
voxel, e.g. (Thacker and Jackson, 2001a). The assign-
ment of discrete labels to each voxel can be tackled in
a variety of ways falling into two broad categories —
supervised and unsupervised. The former includes a
learning step whereby many examples are provided to
the algorithm. In an unsupervised setting there is no
such step. For a supervised example in the context
of grey and white matter segmentation, see (Vrooman
et al., 2007) where spatial coordinates that are known
to correspond to white matter or grey matter are used
as initial seed points to seed a kNN (k-nearest neigh-
bour) classifier.
Semi-supervised approaches are also used. In
(Murgasovaa, 2009) the authors generate a probabilis-
tic atlas and use it to drive the evolution of the EM
algorithm.
On the fully unsupervised side, many papers use
k-means on either single images or pairs of images,
for example (Blatter et al., 1995). (Pham et al., 2000)
gives an overview of all well known segmentation
techniques used in grey matter white matter segmen-
tation up until 2000.
The SFC Brain Imaging Research Centre at the
University of Edinburgh has developed a multispec-
507
C. Valdés Hernández M., M. Wardlaw J. and Murphy S. (2010).
A COMPARISON OF FOUR UNSUPERVISED CLUSTERING ALGORITHMS FOR SEGMENTING BRAIN TISSUE IN MULTI-SPECTRAL MR DATA.
In Proceedings of the Third International Conference on Bio-inspired Systems and Signal Processing, pages 507-514
DOI: 10.5220/0002766005070514
Copyright
c
SciTePress

Figure 1: T2
∗
W, FLAIR, T2 W, T1 W, axial slice of coregistered sequences from a subject after brain extraction.
tral approach for segmenting tissue types in nor-
mal and abnormal brains, including white matter le-
sions (WMLs), based on mapping two magnetic res-
onance (MR) structural sequences in the red/green
colour space and using minimum variance quantisa-
tion (MVQ) to cluster and quantify the tissues. The
current study builds on that work.
For a relevant (albeit dated) comparison between a
supervised and an unsupervised clustering techniques
(neural networks) see (Hall et al., 1992). Due to
the advantages that unsupervised techniques have for
achieving an automatic segmentation process in re-
duced number of steps, we decided to evaluate the
performance of four well-known unsupervised clus-
tering algorithms k-means (MacQueen et al., 1966),
EM (Gaussian mixture) (Dempster et al., 1977),
MVQ (minimum variance quantization) (Xiang and
Joy, 1994) and Mean Shift (Comaniciu and Meer,
2002).
It is known that the use of two or more se-
quences increases the information at each voxel and
aids the automated classification (Thacker and Jack-
son, 2001a). This paper addresses the problem of
fully automated detection of white matter/grey mat-
ter and CSF from a multisprectral image (we used T1
weighted, T2 weighted, T2
∗
weighted and FLAIR), in
an unsupervised setting.
The structure of the paper is as follows. Section
2 details the acquisition parameters of the scans in
question. Section 3 describes the actions performed
on the datasets before they were processed by the au-
tomated algorithms. Section 4 motivates the approach
and graphically explores the problem. Section (5) de-
scribes how the algorithms were validated and how
they operate. It addresses a subtle design choice re-
lating to whether the data should be analysed on a per
slice or volume basis. We then describe the cluster-
ing algorithms used, their merits and their disadvan-
tages. Section (6) states numerically how each algo-
rithm performed.
BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing
508

2 MATERIALS
We use 12 sets of structural MR se-
quences from the Disconnected Mind Study
(http://www.disconnectedmind.org.uk), which
aims to understand how and why some older people’s
cognitive function deteriorates more than others,
and find associations between brain physiology and
cognitive performance in a population of more than
1000 volunteers of the Lothian Birth Cohort 1936.
All MR images were rated for WML and atro-
phy using validated qualitative rating scales (Fazekas
et al., 2002; Longstreth et al., 1996; Wahlund et al.,
1990) by an experienced neuroradiologist (author
JMW). Based on these ratings, the sample for the
present work was selected so as to represent the full
range of WMLs across a range of degrees of brain at-
rophy. The MR sequences in this cohort study were:
• A T1-weighted (T1W) brain volume was ac-
quired (T R = 9ms; T E = 4ms; coronal acquisi-
tion). The 3D volume matrix size was 156×256×
256, with a voxel size of 1.3 × 1 ×1mm
3
.
• A T2-weighted (T2W) brain volume was ac-
quired (T R = 11300ms; T E = 100ms; axial ac-
quisition). The 3D volume matrix size was 80 ×
256 × 256, with a voxel size of 2 × 1 × 1mm
3
.
• A T2
∗
-weighted (T2
∗
W) brain volume was ac-
quired (T R = 940ms; T E = 15ms; axial acquisi-
tion). The 3D volume matrix size was 80×256 ×
256, with a voxel size of 2 × 1 × 1mm
3
.
• A FLAIR brain volume was acquired (T R =
9000ms; T E = 147ms; axial acquisition). The 3D
volume matrix size was 80 × 256 × 256, with a
voxel size of 2 × 1 × 1mm
3
.
Figure 2 shows an axial slice of an individual’s
brain with 3 sequences (T2
∗
W, FLAIR and T1W)
fused into one image, with each one occupying a sin-
gle colour channel (red, green and blue, respectively).
Figure 1 shows the same slice, but as four separate
images. As described below, the images have been
rigidly co-registered and irrelevant material (such as
the skull) has been removed.
3 PREPROCESSING
Each set of four structural sequences per subject were
affinely registered to each other using the FSL appli-
cation FLIRT (http://www.fmrib.ox.ac.uk/fsl/flirt/).
FLIRT is an open source, command line linear reg-
istration tool maintained by the Analysis Group,
Figure 2: The T2
∗
W, FLAIR and T1W sequences fused in
red, green and blue channels, respectively.
FMRIB, Oxford, UK. The volumes were resam-
pled so that they were in the same space and con-
tain the same number of images. The intensities
were manually window-leveled in each volume so
that the intensity ranges in all images were approx-
imately the same. A mask of the brain was gen-
erated using the biomedical imaging software Ana-
lyze (http://www.analyzedirect.com), and in particu-
lar, its seeded region growing segmentation function-
ality, with stopping criteria dependant on thresholds.
The masks were checked for errors and any errors
were manually removed. The brain mask is used to
zero all intensities outside the brain.
4 INVESTIGATION/VALIDITY
A precondition for the previous work is that a given
voxel can be classified into one of the tissue types by
determining the intensities at that voxel together with
the intensity distribution across the entire image. A
first step in determining the validity of this is to visu-
alise the intensity distributions for a given image.
In our context this distribution manifests itself as a
4D joint histogram or scatter plot as shown in Figure
3.
It is evident that there are at least two obvious
clusters which may correspond to different tissue
types. Through experimentation these clusters have
been determined to be grey matter/white matter (i.e.
brain tissue) and CSF. In most projections the grey
matter/white matter cluster is small in extent but in
the T1W projections it has a large extent, with grey
matter at one end and white matter at the other end.
This highlights the fact that T1W is the best sequence
A COMPARISON OF FOUR UNSUPERVISED CLUSTERING ALGORITHMS FOR SEGMENTING BRAIN TISSUE
IN MULTI-SPECTRAL MR DATA
509

Figure 3: Joint histogram (or joint probability distribution) of the four sequences on a portion of the volume shown as
six 2D projections. Each view is an average projection and so represents the marginal probability density for the different
intensity types. The colour represents the probability/frequency at that point with dark blue representing low frequency and
red representing high frequency, on a log scale. The projections have been smoothed. Sequence values are increasing from
left to right and bottom to top. Contributions from the background (zero intensities) have been ignored and do not appear.
for segmenting grey from white matter because it pro-
vides the best contrast between them. It also high-
lights the fact that segmenting grey and white matter
from each other using intensity information only is
problematic because there is a continuum of intensity
ranges between them, with no obvious boundary.
The CSF cluster has high intensity on a T2W scan
and low intensity on T1W. The contrast between brain
tissue and CSF is high in T2W, which again is a
known result. In terms of volume, CSF represents a
far smaller proportion of the brain than brain tissue
and consequently this peak is not as pronounced as
the other.
The clear separation of CSF and brain tissue sug-
gests that an intensity based approach may work. Di-
rect thresholding at predefined levels is unlikely to
work because of the natural variability in MR images
and because there may not be a threshold which sep-
arates them in any one sequence.
5 ALGORITHMIC
DETAILS/JUSTIFICATION
A precondition for the previous work is that a given
voxel can be classified by determining the intensi-
ties at that voxel together with the intensity distribu-
tion across the entire image. A fully automated clus-
tering algorithm analyses the intensity distributions
and partitions the intensity space into four clusters –
background, CSF, grey matter and white matter. The
boundaries between these clusters in feature space are
known as feature space decision boundaries.
5.1 Validation Details
The algorithms were evaluated numerically by com-
paring the automatically generated segmentations to
user collected segmentations which are considered to
be true (ground truth). We used standard comparison
metrics: true positive fraction (TPF), positive predic-
tive value (PPV) and Dice coefficient. The TPF is the
fraction of ground truth which was found (in terms of
volume). The PPV is the fraction of the segmentation
which is correct (in terms of volume). The Dice coef-
ficient combines these two measures into one. In all
cases a value of zero indicates a complete failure and
one indicates a complete success. To be specific, the
Dice metric is defined as:
Dice(X,Y) =
2|X ∩Y |
|X| + |Y |
(1)
where X & Y are the ground truth and generated seg-
mentations, respectively.
BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing
510

Presently, only the correctness of the CSF and
WM segmentations have been evaluated. Intuitively
CSF should be the easiest of the three tissue types to
segment because it seems to be well localised in the
joint histogram and well separated from the other tis-
sue types. On the other hand it might be the hardest
because it has a very high surface area to volume ratio
in comparison to the other tissue types. Since errors
are normally made at the boundary or surface of a re-
gion, those errors will represent a larger percentage
of the total volume of the tissue and so have a larger
effect on the Dice coefficient.
The ground truth was provided by the SFC Brain
Imaging Research Centre. It was semi-automatically
generated using a method developed in-house in the
SFC Brain Imaging Research centre followed by
manual editing by an experienced image analyst (au-
thor MVH). This presents an obvious bias towards
the MVQ algorithm, and consequently the results pre-
sented with regard to the MVQ should be interpreted
with caution.
5.2 Per Slice/Per Volume Analysis
The question arrises as to whether the clustering pro-
cess should proceed on a per volume or per slice ba-
sis. That is, should the clustering algorithms draw
their samples from the entire volume or should they
perform the clustering on each slice individually?
One advantage of the per-slice strategy is a rel-
ative immunity to magnetic field inhomogeneities at
least in the axial direction. Obviously the extent of
this advantage is tied to the severity of the magnetic
field inhomogeneities, which in this experiment are
not significant.
A disadvantage is that, although the total number
of samples in the feature space is the same in every
slice, 128×128, the number of samples in a given tis-
sue type is highly variable between slices. In slices
where a class does not appear in high frequency, there
is an increased risk that it will be incorrectly classi-
fied.
Our investigation suggested that the per volume
strategy significantly outperforms the other in both
total segmentation accuracy and consistency. Conse-
quently from this point on we will refer only to the
results of the whole volume analysis.
5.3 Clustering Algorithms
5.3.1 k-Means
The k-means algorithm is an iterative clustering al-
gorithm which, given a set of multidimensional data,
which it interprets as points in a Euclidean space, par-
titions it into a given number of clusters k such that
the sum of the Euclidean distance squared from each
point to its respective cluster center is approximately
minimal. The k-means algorithm (MacQueen et al.,
1966) can be applied directly to the intensities to ac-
quire a partition. In this experiment, four clusters are
Figure 4: k-means intensity classifications over T1W &
T2W. CSF, grey matter and white matter are coloured in
blue, red and yellow, respectively.
requested and the k-means search is initialised with
known approximate intensities for the different tis-
sue types. As expected, the feature space decision
boundaries on the resultant classifier are composed
of straight hyper-planes in the 4-dimensional feature
space. It is almost certainly the case that the optimal
feature space decision boundaries, are not a collec-
tion of hyper-planes. Despite producing physically
unrealistic feature space decision boundaries in this
way, it has still performed well as shown in the results
section, and has chosen to split the white-matter/grey
matter distributions.
5.3.2 EM
The expectation-maximization (EM) algorithm finds
a set of statistical model parameters which best ex-
plains a given set of observed data, in the presence of
unobserved latent variables. It does this by determin-
ing the set of parameters which maximise the likeli-
hood of the data. The EM algorithm was explained
and given its name in (Dempster et al., 1977). It is an
iterative method that alternates between an expecta-
tion stage, which calculates the distribution of the la-
tent variables given the parameters of the model, and
a maximisation stage, which determines the set of pa-
rameters of the model that maximises the expectation
of the likelihood of the data. In the context of this
paper, we seek to model the joint probability density
function of the points within the brain as a function
of their intensities in each sequence. The probabilis-
tic model is deemed to be a mixture of a fixed num-
ber of Gaussian distributions, where the means, co-
A COMPARISON OF FOUR UNSUPERVISED CLUSTERING ALGORITHMS FOR SEGMENTING BRAIN TISSUE
IN MULTI-SPECTRAL MR DATA
511
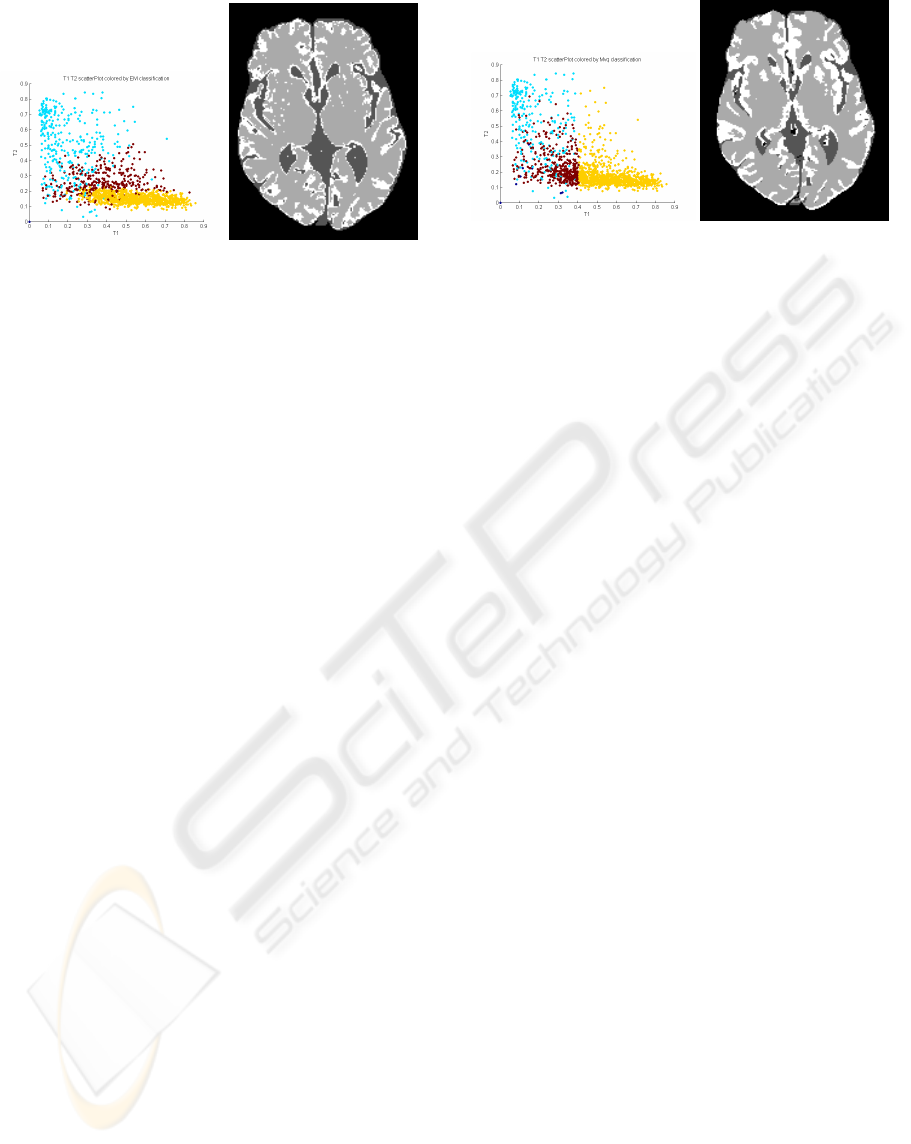
Figure 5: EM intensity classifications over T1W & T2W.
CSF, grey matter and white matter are coloured in blue, red
and yellow, respectively.
variances and weights of the Gaussians are allowed to
vary. In this case, the latent variables determine which
Gaussian distribution each sample belongs to. We ini-
tialise the EM algorithm with approximate parameters
which have been determined a priori to relate to tissue
types. Thus, once the EM algorithm has converged
and the Gaussian mixture has been determined, we
can directly assign a tissue type to each Gaussian dis-
tribution. We can then partition the image into tis-
sue types by determining which of the Gaussians it
is most likely a member of by using the maximum
posterior probably. For this experiment we removed
the background intensities from the set of voxels to
be classified because this caused the EM algorithm to
fail to converge. The minimum number of distribu-
tions for which the EM algorithm would give a sensi-
ble result was four. In practice, CSF was deemed to
be the union of two found class types, whereas grey
matter and white matter were represented by the other
2 classes.
The feature space decision boundaries produced
by this clustering algorithm can be shown to be com-
posed of quadratic surfaces, and so are, in general,
curved. This can be seen in figure 5. Intuitively, these
decision boundaries would be more like the optimal
decision boundaries by virtue of the fact that they are
curved. Despite this, it did not perform the best. In
general it seemed to over-segment the white matter
and under-segment grey matter. It also seemed to pro-
duce noisier segmentations.
5.3.3 MVQ
The minimum variance quantisation (MVQ) algo-
rithm (Xiang and Joy, 1994) is used in image process-
ing and compression for reducing the colour depth of
an image, for example, from 65535 to 256. It pro-
duces noticeably better quality images by respecting
the distributions of the colours in the image. More
specifically it aims to minimise the variance (sum
Figure 6: MVQ intensity classifications over T1W & T2W.
CSF, grey matter and white matter are coloured in blue, red
and yellow, respectively.
squared difference) between input image and the out-
put image. The class of partitions it considers are box
partitions (i.e. the partition surfaces are orthogonal
hyper-planes). In common with the other clustering
algorithms considered here, MVQ uses no spatial in-
formation. It can be interpreted as a clustering algo-
rithm and this is how it is used in this experiment. We
set the algorithm to quantise the number of colours
in the fused image to four, and these colours are in-
terpreted as the different tissue types. The algorithm
can be generalised to N dimensions but typically (as
in MATLAB’s implementation) it is limited to three
dimensions, (red, green, blue) and so we must ignore
one of the channels (T2W).
This algorithm performed very well, although pro-
duced some physically unrealistic feature space deci-
sion boundaries.
5.3.4 Mean Shift
The mean shift algorithm (Comaniciu and Meer,
2002) is a non-parametric feature space analysis tech-
nique, which determines the gradient in feature space
at any point. This can be used to find basins of at-
traction which partition the space, and consequently
assign each point in the feature space to a cluster.
Unlike the other algorithms the user does not supply
the number of clusters as this is determined automati-
cally. Instead the user supplies a radial basis function
which is normally (as in this case) a spherically sym-
metric Gaussian distribution, centered at zero with a
specified variance (or scale). Increasing the variance
tends to decrease the number of clusters. For this ex-
periment the scale parameter was tuned until the num-
ber of clusters was three or four.
Despite being one of the more elegant of the
clustering algorithms, its slow runtime and inability
to discriminate white matter from grey matter con-
tributed to its early disqualification, and so it has not
been quantitatively evaluated. Its slow runtime is ac-
credited to its MATLAB implementation (the others
BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing
512

Figure 7: Mean shift intensity classifications over T1W &
T2W. CSF and grey matter/white matter are coloured in
green and blue, respectively.
are coded in C) and its inability to discriminate white
matter from grey matter is likely due to the fact that
they lie in the same attractive basin and so will never
be split into different partitions. On the other hand,
this clustering algorithm seemed to be very sensitive
to small but definite intensity features, and may prove
suited to the detection of pathologies such as WMLs
— this has not yet been investigated.
6 RESULTS AND DISCUSSION
The quantitative results from 12 datasets can be seen
in tables 1, 2 and 3. As explained above, the mean
shift algorithm has not been quantitatively evaluated.
Looking at the average Dice coefficient for CSF we
see that MVQ performs best although the validation
is biased towards it (see section 5.1). EM also has
performed well, and has a number of desirable prop-
erties which the k-means or the MVQ lack, such as
the ability to assign a probability of a voxel being in
a given tissue classification, which can improve vol-
ume measurement accuracy, see (Thacker and Jack-
son, 2001b), amongst other advantages. Looking at
the scores relating to white matter however, we see
that k-means performs best of all, with 91% accuracy.
ACKNOWLEDGEMENTS
These experiments were undertaken as part of an
EngD with ISLI (Institute of System Level Inte-
gration - http://www.isli.co.uk/ - EPSRC) as the
sponsor. The work was undertaken at SBIRC
(the SFC Scottish Imaging Research Centre -
http://www.sbirc.ed.ac.uk).
The datasets and ground truth used in these ex-
periments were collected as part of the Disconnected
Table 1: k-means: Dice coefficients for CSF and white mat-
ter for the k-means clustering algorithm. Confidence values
calculated at 99% using student-t distribution. White mat-
ter ground truth is missing for datasets Sub1, Sub2 and Sub3
and so these do not appear.
k-means
Dataset CSF WM
Sub1 .72
Sub2 .71
Sub3 .73
Z01 .72 .9
Z02 .72 .96
Z03 .73 .92
Z04 .81 .89
Z11 .73 .95
Z14 .74 .95
Z16 .78 .7
Z17 .77 .95
Z19 .7 .95
Average .74 ± .03 .91 ± .1
Table 2: MVQ: Dice coefficients for CSF and white matter
for the MVQ clustering algorithm. Confidence values cal-
culated at 99% using student-t distribution. White matter
ground truth is missing for datasets Sub1, Sub2 and Sub3
and so these do not appear.
MVQ
Dataset CSF WM
Sub1 .86
Sub2 .91
Sub3 .91
Z01 .91 .84
Z02 .92 .89
Z03 .87 .76
Z04 .91 .75
Z11 .91 .88
Z14 .9 .89
Z16 .85 .6
Z17 .92 .84
Z19 .9 .86
Average .9 ± .02 .81 ± .11
Mind Project (http://www.disconnectedmind.org.uk).
The Disconnected Mind Project is funded by Help
the Aged (http://www.helptheaged.org.uk/en-gb) and
the UK Medical Research Council. The SFC
Brain Imaging Centre is part of the Scottish Imag-
ing Network, a Platform for Scientific Excellence
(SINAPSE, http://www.sinapse.ac.uk); author JMW
is part funded by the SINAPSE collaboration.
Thanks to Ian Poole and Y. R. Petillot for their
involvement and input.
A COMPARISON OF FOUR UNSUPERVISED CLUSTERING ALGORITHMS FOR SEGMENTING BRAIN TISSUE
IN MULTI-SPECTRAL MR DATA
513

Table 3: EM: Dice coefficients for CSF and white matter for
the EM clustering algorithm. Confidence values calculated
at 99% using student-t distribution. White matter ground
truth is missing for datasets Sub1, Sub2 and Sub3 and so
these do not appear.
EM
Dataset CSF WM
Sub1 .86
Sub2 .8
Sub3 .73
Z01 .7 .79
Z02 .68 .9
Z03 .75 .74
Z04 .76 .72
Z11 .83 .8
Z14 .78 .76
Z16 .81 .7
Z17 .76 .87
Z19 .71 .76
Average .76 ± .04 .78 ± .08
REFERENCES
Blatter, D., Bigler, E., Gale, S., Johnson, S., Anderson, C.,
Burnett, B., Parker, N., Kurth, S., and Horn, S. (1995).
Quantitative volumetric analysis of brain MR: norma-
tive database spanning 5 decades of life. American
Journal of Neuroradiology, 16(2):241–251.
Burton, E., Karas, G., Paling, S., Barber, R., Williams, E.,
Ballard, C., McKeith, I., Scheltens, P., Barkhof, F.,
and O’Brien, J. (2002). Patterns of cerebral atrophy in
dementia with Lewy bodies using voxel-based mor-
phometry. Neuroimage, 17(2):618–630.
Busatto, G., Garrido, G., Almeida, O., Castro, C., Camargo,
C., Cid, C., Buchpiguel, C., Furuie, S., and Bottino, C.
(2003). A voxel-based morphometry study of tempo-
ral lobe gray matter reductions in Alzheimers disease.
Neurobiology of aging, 24(2):221–231.
Comaniciu, D. and Meer, P. (2002). Mean shift: A robust
approach toward feature space analysis. IEEE Trans-
actions on pattern analysis and machine intelligence,
pages 603–619.
Crum, W. (2007). Spectral Clustering and Label Fusion For
3D Tissue Classification: Sensitivity and Consistency
Analysis.
Dempster, A., Laird, N., Rubin, D., et al. (1977). Maxi-
mum likelihood from incomplete data via the EM al-
gorithm. Journal of the Royal Statistical Society. Se-
ries B (Methodological), 39(1):1–38.
Fazekas, F., Barkhof, F., Wahlund, L., Pantoni, L., Erkin-
juntti, T., Scheltens, P., and Schmidt, R. (2002). CT
and MRI rating of white matter lesions. Cerebrovas-
cular Diseases, 13:31–36.
Good, C., Johnsrude, I., Ashburner, J., Henson, R., Friston,
K., and Frackowiak, R. (2001). A voxel-based mor-
phometric study of ageing in 465 normal adult human
brains. Neuroimage, 14(1):21–36.
Hall, L., Bensaid, A., Clarke, L., Velthuizen, R., Silbiger,
M., and Bezdek, J. (1992). A comparison of neural
network and fuzzy clustering techniques insegment-
ing magnetic resonance images of the brain. IEEE
Transactions on Neural Networks, 3(5):672–682.
Head, D., Snyder, A., Girton, L., Morris, J., and Buckner,
R. (2005). Frontal-hippocampal double dissociation
between normal aging and Alzheimer’s disease. Cere-
bral Cortex, 15(6):732–739.
Lehtovirta, M., Laakso, M., Soininen, H., Helisalmi, S.,
Mannermaa, A., Helkala, E., Partanen, K., Ryyn
¨
anen,
M., Vainio, P., Hartikainen, P., et al. (1995). Vol-
umes of hippocampus, amygdala and frontal lobe in
Alzheimer patients with different apolipoprotein E
genotypes. Neuroscience, 67(1):65–72.
Longstreth, W., Manolio, T., Arnold, A., Burke, G., Bryan,
N., Jungreis, C., Enright, P., O’Leary, D., and Fried,
L. (1996). Clinical correlates of white matter findings
on cranial magnetic resonance imaging of 3301 el-
derly people The Cardiovascular Health Study. Stroke,
27(8):1274–1282.
MacQueen, J. et al. (1966). Some methods for classification
and analysis of multivariate observations.
Miller, A., Alston, R., and Corsellis, J. (1980). Variation
with age in the volumes of grey and white matter in
the cerebral hemispheres of man: measurements with
an image analyser. Neuropathology and applied neu-
robiology, 6(2):119–132.
Murgasovaa, M. (2009). Construction of a dynamic 4D
probabilistic atlas for the developing brain.
Pham, D., Xu, C., and Prince, J. (2000). Current Methods
In Medical Image Segmentation 1. Annual Review of
Biomedical Engineering, 2(1):315–337.
Thacker, N. and Jackson, A. (2001a). Mathematical seg-
mentation of grey matter, white matter and cerebral
spinal fluid from MR image pairs. British Journal of
Radiology, 74(879):234.
Thacker, N. and Jackson, A. (2001b). Mathematical seg-
mentation of grey matter, white matter and cerebral
spinal fluid from MR image pairs. British Journal of
Radiology, 74(879):234.
Vrooman, H., Cocosco, C., van der Lijn, F., Stokking, R.,
Ikram, M., Vernooij, M., Breteler, M., and Niessen,
W. (2007). Multi-spectral brain tissue segmentation
using automatically trained k-nearest-neighbor classi-
fication. Neuroimage, 37(1):71–81.
Wahlund, L., Agartz, I., Almqvist, O., Basun, H., Forssell,
L., Saaf, J., and Wetterberg, L. (1990). The brain in
healthy aged individuals: MR imaging. Radiology,
174(3):675–679.
Xiang, Z. and Joy, G. (1994). Color image quantization by
agglomerative clustering. IEEE Computer Graphics
and Applications, 14(3):44–48.
BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing
514
