PROBLEM-BASED LEARNING

A Graph Theory Experience

Mar´ıa Ang´elica Pinninghoff J., Ricardo Contreras A.

Department of Computer Science, University of Concepci´on, Chile

Pedro Salcedo L.

Department of Research and Educational Informatics, University of Concepci´on, Chile

Keywords:

Problem-based learning, Graph theory, Engineering education.

Abstract:

Problem-based learning is a widely used technique in supporting different educational efforts, in which the

core idea is to understand a real problem and, starting from this point, to seek the elements that are necessary

to solve it. This work presents an experience that shows the results of applying this technique in a typical com-

puter science topic in a classical engineering curriculum. Preliminary results obtained by using this technique

are discussed, and some directions for future work are proposed.

1 INTRODUCTION

Problem-Based Learning (PBL) can be deﬁned as an

inquiry process that resolves questions, curiosities,

doubts, and uncertainties about complex phenomena

in life. A problem is any doubt, difﬁculty, or uncer-

tainty that invites or needs some kind of resolution.

According to (Barell, 2007), student inquiry is very

much an integral part of PBL and problem resolution.

In other words, PBL requires to establish a classroom

environment that welcomes questioning and differ-

ent points of view, and that thrives on collaboration

among all participants.

PBL was ﬁrst applied in the 60s, to health sci-

ences teaching; in the Faculty of Health Sciences of

McMaster University, Canada (Walsh, 2005), and in

the School of Medicine of Case Western Reserve Uni-

versity, USA, trying to reach two fundamental goals:

to develop problem solving skills in students and to

place learning closer to real problems. This success-

ful experience was rapidly spread from medical and

professional schools to different disciplines.

Currently, this strategy is implemented as a learn-

ing environment in which the problem drives the

learning, i.e., a problem is presented to the students

before they rally acquire any knowledge. The idea

is that the students have to discover that they need

to learn some new knowledge, before they can solve

the problem. If a problem is presented to a student

before learning, for them it becomes a more motivat-

ing activity. This happens because in the seek of new

knowledge, students really know why they are learn-

ing. Additionally, learning triggered by the need to

solve a problem, allows to store that knowledge in

the form of patterns that later, when necessary, can

be easily retrieved.

Table 1 shows different learning structures in

PBL and traditional learning methodologies (Garcia-

Famoso, 2005):

One important point to remark is that PBL is not

problem solving. Problem solving is the process used

to solve a problem, so the students involved in a PBL

process should be skilled in solving problems or, at

least, in critical thinking. The case-based approach

strategy, on the other hand, usually integrates exist-

ing knowledge; and therefore is not, according to the

previous assessment, problem-based learning.

Keeping in mind the idea of a new learning

paradigm, it is important to be aware that students

should be guided towards solutions, and not be driven

towards them. This means that tutors must let each

group make a reasonable attempt at the set problems

before intervening. This can lead to the fact that the

same explanation should be given to different groups

at different times.

Angélica Pinninghoff J. M., Contreras A. R. and Salcedo L. P. (2010).

PROBLEM-BASED LEARNING - A Graph Theory Experience.

In Proceedings of the 2nd International Conference on Computer Suppor ted Education, pages 79-83

DOI: 10.5220/0002768700790083

 SciTePress

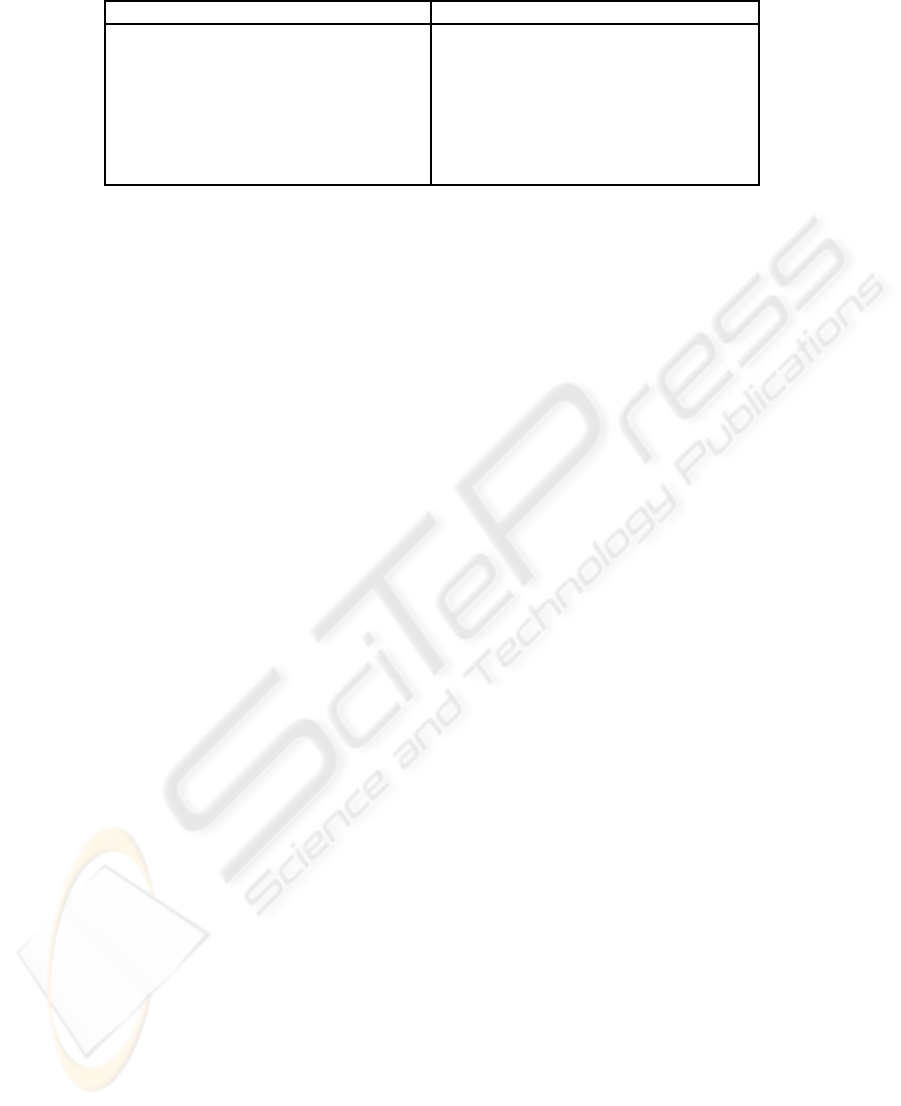
Table 1: PBL and traditional learning structures.

Traditional Methodologies Problem-Based Learning

Teacher centered Student centered

Linear and rational Coherent and relevant

Teacher as transmitter Instructor as facilitator or collaborator

Students as passive receivers Students as constructors. Active

Structured environment Flexible environment

Individual and competitive Co-operative

Assessment is a teacher responsibility Assessment is a shared responsibility

The aim of this work is to show the results of intro-

ducing PBL in an engineering course. The inclusion

of PBL in the course Graphs and Algorithms was ac-

complished having in mind that the key objective is

to familiarize students with this model. Furthermore,

the core idea is to show that this strategy can help in

keeping students’ interest when exposed to particular

subjects. As expected, this approach presents some

pros and cons, that are mentioned in the conclusions.

This article is structured as follows; the ﬁrst sec-

tion is made up of the present introduction; the second

section describes some previous experiences in com-

puter science related to the speciﬁc topic to be dealt

with; the third section is devoted to our particular ex-

perience, while the fourth section shows the prelimi-

nary results we obtained with our approach, and the

ﬁnal section shows the conclusions of the work.

2 PBL IN COMPUTER SCIENCE

The traditional approach, for teaching speciﬁc top-

ics in computer science, has been carried out in a

sequence that considers the introduction of concep-

tual material in lectures. This material is comple-

mented with a set of examples and a set of exercises.

Sometimes, these activities are supported with practi-

cal work in laboratory sessions.

While pioneer work in PBL is associated to med-

ical learning; computer science, as a discipline, is

playing an important role in the application of this

paradigm. We can mention the work in the School

of Computer Science and Information Technology in

Melbourne, Australia, which describes the experience

of dealing with a speciﬁc topic: computing theory.

We share with the authors the perception that by us-

ing PBL, students are more involved in the teaching

learning process (Hamilton et al., 2003).

Positive results in computer science are also re-

ported in (Chinn and Martin, 2005), where authors

describe the experience carried out in the Institute

of Technology, University of Washington, Tacoma.

They combine the use of PBL with collaborative

learning, and describe the design and implementation

of such learning environment for courses in the be-

ginning sequence of a computer science program. In

computer science, thetop-down approach of introduc-

ing different topics in lectures, reinforcing it with ex-

amples, and applying it as a kind of magic recipe, fre-

quently leads to a lack of motivation, due in part to

the nature of the topics, and in part (and most impor-

tant) because its applications are not clear in advance

(Hamilton et al., 2003).

A recent work (dos Santos et al., 2009) propose an

innovativepedagogicalmethodology based on PBL to

improve the learning effectiveness in software engi-

neering, through the implementation of software fac-

tories, where students can work together to solve real

problems.

PBL has been applied in graduate programs, as re-

ported in (Linge and Parsons, 2006), that addresses

the challenge of developing techniques for the ef-

fective teaching of computer network design, within

the context of a master’s program module and using

a two-threaded approach, that comprised a problem-

based learning thread and a conventional lecture

thread.

3 TEACHING GRAPH THEORY

WITH PBL

We have selected a speciﬁc course in computer sci-

ence: Graphs and Algorithms. It is necessary to no-

tice that the ﬁrst step was to switch from the classic

concept of chapter to the concept of unit. Units help

ensure that all the various activities add up to mean-

ingful learnings. Chapters, on the other hand, don’t

help to students’ inquiry, because of the long period

devoted to a chapter coverage, compared to the lim-

ited, and typically short time associated to a speciﬁc

unit.

PBL can be carried out in a collaborative learning

environment, which is the case under discussion, or

CSEDU 2010 - 2nd International Conference on Computer Supported Education

it can be carried out as an individual project; in the

latter it doesn’t require cooperation among students.

We have chosen the collaborative environment as op-

posed to a competitive one, where students are in a

race against each other in order to get best marks, be-

cause this is the model they will ﬁnd in a real working

place.

3.1 Basic Considerations

We have selected Graph Theory based on the premise

that this subject is widely considered conceptually

difﬁcult, but accepting that it’s strongly connected

to interesting and real problems. The traditional ap-

proach to this subject ﬁnishes a speciﬁc topic by

showing a well known problem that students under-

stand but that simply appears. We think that, from

this perspective, students need to start a backtracking

process to grasp how different concepts, previously

seen, are assembled to obtain a solution. The PBL

approach, on the other hand, encourages a search pro-

cess having in mind the problem to be solved.

As a ﬁrst step in the introduction of PBL, we de-

cided to address the effort devoted to introduce the

new paradigm in a speciﬁc unit: spanning trees. In

simple words, a spanning tree is a set of nodes (e.g.,

points representing locations) having one condition;

all of them are connected, i.e., given two arbitrary

chosen nodes, there is a path between them. If we add

the condition that the cost of connecting all the nodes

is as low as possible, we are dealing with a mini-

mum spanning tree. In doing so, we decided to imple-

ment a two thread view for the speciﬁc unit (spanning

trees). It means that the PBL strategy was adopted

when working with the speciﬁc problem concerning

minimum spanning trees, as described in the next sub-

section, and as a second thread we supported students

with conventional lectures, aimed to solve doubts and

to provide key concepts.

3.2 The Particular Assignment

The speciﬁcations of the ﬁrst assignment used in 2009

is shown below.

Main objective from the teacher perspective: To

develop a graph-based model to describe an optimiza-

tion problem, ﬁnding a spanning tree that solves the

problem.

Learning objectives from the teachers perspective:

i) to understand the beneﬁts of modeling problems by

using graphs; students have to construct a graph with

labeled arcs that represent an instance of cost; ii) to

know how speciﬁc algorithms (i.e., Prim and Kruskal)

help to get spanning trees; iii) to develop the capa-

bility of modeling problems using graphs; iv) to im-

plement a mechanism that allows to solve the posed

problem.

The problem presented to the students is the fol-

lowing: This class is going to develop a physical con-

nection using optic ﬁber, in order to have all the stu-

dents connected to the university network. Due to

economic constraints, students divided into groups,

each of which is independent in terms of connectivity.

Students belonging to a particular group can be con-

nected among themselves and, at least one member

of each group is connected to the university network,

trying to ﬁnd a minimum cost solution. It is neces-

sary to determine how much optic ﬁber is necessary

to implement the solution.

Students had to submit two written reports, a soft-

ware operating on real data and a ﬁnal presentation.

Students were classiﬁed in groups of 3 or 4 members,

randomly chosen. For the ﬁrst report delivery, each

one of these groups modeled the problem concern-

ing only students involved in the group. This helped

to understand the problem and to take into account

the criteria of the group in order to decide the selec-

tion of a particular model. For the second report de-

livery, each group shares the collected data with all

the other groups. In doing so, each group is able to

implement a particular solution, based on their own

models, by considering the complete population to be

connected. The implemented solution is a software

product which is described in the second report. Fi-

nally, each one of the groups developed a presentation

for analyzing the experience from their own points of

view.

4 PRELIMINARY RESULTS

In this ﬁrst experience with PBL, the results havebeen

interesting. Students showed a high level of inter-

action, and class attendance (that is not mandatory)

presented very good ratings, compared to the tradi-

tional scheme. In the different steps during this ex-

perience, students became actively involved, giving

opinions and asking for different concepts related to

the topic.

It is a policy in the University, to ask the students

for an anonymous evaluation about teaching. This is

accomplished via web, so students do not need to be

physically at the university; in fact, most of them an-

swer the questions during vacations. Among the dif-

ferent aspects considered in this anonymous require-

ment, the ability to teach is evaluated. The main point

PROBLEM-BASED LEARNING - A Graph Theory Experience

here is that the lecturer for this class is the same one

they’ve had for a long period, starting in 2000. The

best previous mark the lecturer was given was 5.48

(in a 1 to 7 interval), whereas in 2009, with students

emphasizing the PBL experience, this mark raised up

to 5.8. This is illustrated in Figure 1.

Figure 1: Teacher evaluation evolution.

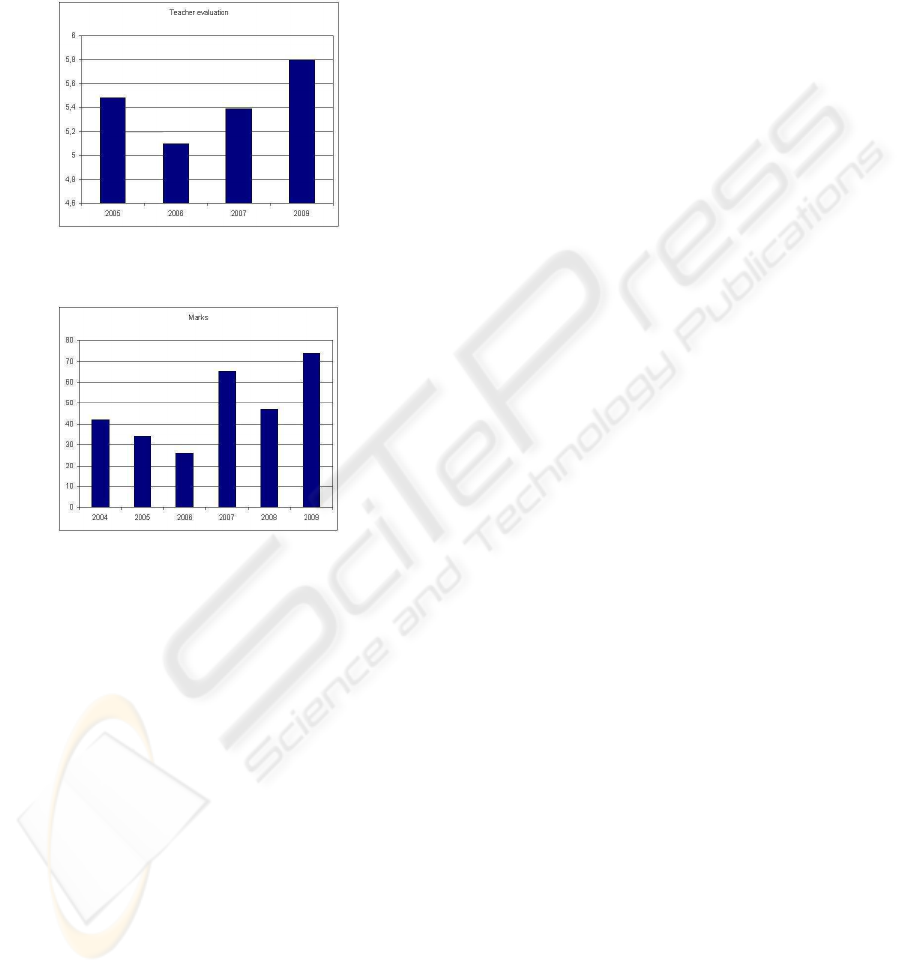
Figure 2: Evolution of marks in Graphs and Algorithms.

In respect to marks obtained by the students, a

statistic for Graphs and Algorithms shows how marks

ﬁt in the different considered ranges. To simplify

this, Figure 2 shows marks corresponding to the upper

range (that goes from 4.6 to 7) starting with data from

2004. In other words, for the ﬁrst time in six years,

more than 70% of the students got marks in the upper

range of the evaluation interval, whereas the previous

top value recorded was 65% of the students.

Even though it is very early in the process to infer

that PBL improves understanding, interest and, as a

consequence, better marks, there is a strong evidence,

based on the students’ opinions, that it can be a help-

ful tool in the teaching process.

These increased marks, and a better perception

about the teacher’s capability for teaching may be a

singular point. The novelty of this approach may lead

to students to accept changes in the teaching-learning

process more easily, and time will let us judge more

accurately this particular issue. But we ﬁrmly believe

that the positive outcomes PBL offers to the teaching-

learning process should not be ignored. And this is the

reason why we are encouraging this teaching strategy.

5 CONCLUSIONS

The idea of introducing a new teaching paradigm that

challenges traditional teaching has been positively

considered by the actors involved in the process. Stu-

dents became gradually interested in the process, and

from a passive attitude the level of interaction evolved

to a very participative process.

Students have found that PBL approach is more

stimulating than standard lectures. The need to deal

with a problem that can be easily understood, al-

though solving the problem may be a hard work, it

motivates students to work in a collaborative perspec-

tive. To place the problem as a central issue that needs

to be solved in teamwork, is a new approach for most

of the students, where they understand and experience

the effects of working in a non competitive approach.

The positive students’ evaluation highlights the

fact that they had the opportunity of working in dif-

ferent scenarios that had a very important practical

dimension and realism.

It is important to notice that students were really

involved in this process, we can illustrate this through

a simple fact: in order to have a closer contact with

the problem, they used Google Earth to obtain precise

distances to work with. The importance of having an

almost real problem acts as a motivating element. In

future planning this fact needs to be taken into ac-

count. An important difference deals with evaluation.

In this experience, the evaluation process considers

a project in which students are actively involved, in-

stead of passive assessments, as it is usually done in

classic teaching.

The teacher’s opinion is that the additional effort,

devoted to material preparation and time for answer-

ing questions about the problem is highly rewarding,

as students get, in their own style and time, a way to

solve a particular situation.

No doubt, this experience needs to be spread out

by including more topics and more courses, and there

is still a lot of work to be done. Nevertheless, it seems

to be a good starting point.

Future directions to be implemented in 2010, con-

sider to increase the number of topics in Graph and

Algorithms, in order to have a PBL strategy for a com-

plete course. These topics should include graph color-

ing and planar graphs, among others. Besides that, it

is time to include the PBL strategy in another course,

and Software Engineering looks like a good choice.

CSEDU 2010 - 2nd International Conference on Computer Supported Education

ACKNOWLEDGEMENTS

This work has been partially supported by grant

DIRDOC 07-014, University of Concepci´on, Chile.

REFERENCES

Barell, J. (2007). Problem-Based Learning. An Inquiry Ap-

proach. Corwin Press, 2nd edition.

Chinn, D. and Martin, K. (2005). Collaborative, problem-

based learning in computer science. In Journal of

Computing Sciences in Colleges, Volume 21, Issue 1.

Consortium for Computing Sciences in Colleges.

dos Santos et al., S. (2009). Applying PBL in software en-

gineering education. In 22nd Conference on Software

Engineering Education and Training. IEEE Computer

Society.

Garcia-Famoso, M. (2005). Problem-based learning: a case

study in computer science. In III International Confer-

ence on Multimedia and Information and Communi-

cation Technologies in Education. Formatex Research

Center.

Hamilton, M., Harland, J., and Padgham, L. (2003). Ex-

periences in teaching computing theory via aspects

of problem-based learning. In Proceedings of the

Fifth Australasian Computing Education Conference

(ACE’03), Adelaide. Australian Computer Society,

Inc.

Linge, N. and Parsons, D. (2006). Problem-based learning

as an effective tool for teaching computer network de-

sign. In IEEE Transactions on Education, Vol. 49, No.

1. IEEE Digital Library.

Walsh, A. (2005). The Tutor in Problem-Based Learning,

a Novice’s Guide. McMaster University, Faculty of

Health Science, 2nd edition.

PROBLEM-BASED LEARNING - A Graph Theory Experience