MODELING THE FRAGILE ECONOMIC SITUATIONS

Stasys Girdzijauskas

Vilnius University, Kaunas Faculty of Humanities, Department of Informatics, Muitines str. 8

LT-44280, Kaunas, Lithuania

Andzela Mialik, Ramunas Mackevicius

Vilnius University, Kaunas Faculty of Humanities, Muitines str. 8, LT-44280, Kaunas, Lithuania

Keywords: Modeling of economic situations, Economic bubbles, Logistic model, Predict.

Abstract: The development of the modern society is dependent on its economic growth. In the given logistic theory, a

uniform system of the scientific statements, calculations and estimations has been maintained. An automatic

computer model for fragile economic situations has already been worked out. Yet better results in the

comprehension of the model are achieved when all the calculations are done manually, with the help of the

MS Excel. Therefore the paper introduces the teaching method that might be helpful in understanding how

to operate with the model in a non-automatic way.

1 INTRODUCTION

The world seems to have been enchained by the

constantly appearing financial problems that alarm

both the ordinary people and scientists who get more

and more involved in the analysis of the causes of

the crises. Research is carried out each year with the

goal of discovering the crisis prediction

mechanisms. That is why it is essential to start

teaching the students to understand the causes

determining the fragile economic situations and

show how should be modeled.

Relevance of the Topic.

The difficulties in the

economic crisis prediction, the frequent

misunderstanding of the fundamental basics of the

reasons and development of such crises, as well as

the real possibility of the financial shocks create the

assumptions for an uneven economic development

thus causing an appearance of the threat of social

convulsions.

In 2002–2006, an original theory of the capital

management was worked out at Vilnius University

(Lithuania). It has been discovered that the logistic

growth seems to be based on the idea so well

expressed by an American author Flannery

O'Connor in the very title of her short story

collection "Everything That Rises Must Converge”

(1965). In economics, however, this principle has

started to be applied only recently (Girdzijauskas S.,

Streimikiene D., Dubnikovas M., 2009).

The discussed logistic analysis is based on the

fundamental principles developed in the classical

financial theory. (Merkevicius E. et al., 2007). Based

on the mentioned theory of logistic growth, the

special curricula have been structured, which more

and more often are found as urgent and therefore are

successfully developed. Today, since the consistent

patterns of economics still do astonish the mankind,

the university students of the appropriate study

programs should be taught to recognize and model

various economic situations.

The logistic theory is much more complex than

the classical financial analysis, and no doubt, its

mastery requires the specific resources for learning.

The objective of the paper is to

comprehensively and visually demonstrate the

algorithm of the economic heat and bubble

formation.

The main tasks of the paper are:

• to present how the fragile economic situations

are formed and to give an example,

graphically and comprehensively

demonstrating the process of the bubble

formation;

167

Girdzijauskas S., Mialik A. and Mackevicius R. (2010).

MODELING THE FRAGILE ECONOMIC SITUATIONS.

In Proceedings of the 2nd International Conference on Computer Supported Education, pages 167-170

DOI: 10.5220/0002770401670170

 SciTePress

• to help the students in understanding the

effectiveness of the logistic model in

analyzing the fragile economic situations.

2 LOGISTIC MODELING

The logistic model is applied for the growing

populations. Moreover, it should be stressed that

growth itself is proportional to the size of the same

population and has a determined growth limit. The

paper aims to reveal how the comprehension process

can be simplified by visualizing the modeling

(Girdzijauskas S., Pikturna A., et al., 2008).

In order to employ the principle of logistic

growth in calculations, one should have the general

understanding of the phenomenon of the exponential

change, that may be conveniently expressed by a

differential Equation 1 (Girdzijauskas S., 2006, p.

65).

∫∫

⋅= dtk

(1)

here K is accumulated capital (the amount of the

product at the time t); k is the coefficient of

proportionality (constant quantity); K

=K(t=0)

(ibid.).

Modeling the growth of the capital on the basis

of this equation, the growth is found to be infinite. In

other words, it is obvious that the equation cannot be

used to predict the long term capital growth

(Girdzijauskas S., 2008).

Already in the 19

century, while studying the

alterations in the biological systems, P. F. Verhülst

suggested to add a multiplier to the differential

equation which has the character of a linearly

decreasing function. Let's apply a similar growth-

limiting multiplier to the differential product

alteration equation (Girdzijauskas S., 2006, p. 277):

⋅⋅

⎟

⎠

⎞

⎜

⎝

⎛

−= ln1

(2)

(

)

()

−++

+⋅⋅

iKK

(3)

here K

is initial capital; K

points to potential

capital expressed in the capital amount estimating

units; i is the rate of interest; n is the number of the

periods of accumulation.

The method of the internal rate of return is one of

the essential means in project estimation. When

calculating the internal rate of return by using the

logistic method, it is necessary to know the potential

capital K

of each member of the payment chain

(Moskaliova V., Girdzijauskas S., 2006, p. 91). Then

the following equation is worked out:

()

+⋅−+

⋅

∑

jpj

iKKK

(4)

The analysis of the logistic net present value of

the money flows and of the internal rate of return

show that the effectiveness of an investment (in

other words, internal return) depends on the degree

of the market filling by the investment capital.

(Girdzijauskas S., Streimikiene D. et al, 2009,

p.267). Thus, the estimation of the growth resources

within the frame of the logistic capital theory turns

to be one of the most important tasks in solving the

problems of rational capital management.

By adapting the particular software tools and

performing the logistic analysis, the economic

bubbles and other economic phenomena that make

the cause of recessions and crises might be

discovered.

For precision, let's explore the heat (growth of

the bubble) model within the following example

table 1:

The investment project is determined to be

realized within 5 years. The net present value (in

complex and logistic percentage) with the rate of

return: a) 10 %; b) 20 % should be calculated as

well as the internal rate of. To perform the logistic

calculations it is necessary to take the following:

Є[1; ∞) of the conditional monetary unit.

Table 1: Money investment flows.

Year

Monetary flows at the end of the year

Expenses Income Total

0 -1 0 -1

1 -0.5 0 -0.5

2 -0.5 1 0.5

3 -0.5 1 0.5

4 -0.5 1 0.5

5 0 1 1

Total: -3 4 1

Source: worked out by the authors

Let's explore the profitability of an investment in

two ways: (a) by using the complex percentage rule

(when the capacity of the market is unlimited); (b)

by employing the logistic analysis (when the

capacity of the market is limited).

Under the initial condition, we have the

following: K

= -1, …, K

= 1; i = 8 % (case a)) and

i = 12 % (case b)).

CSEDU 2010 - 2nd International Conference on Computer Supported Education

168

Further steps will show the ordinary or typical

calculations. With the help of the Microsoft Excel

programme it has been discovered that the IRR

(internal rate of return) of the project is as follows:

IRR = 16.32 %.

Let's calculate the net present value on the basis

of the complex percentage, with the internal rate of

return making: a) 10%, b) 20%. The following

values have been obtained: NPV(0.1) = 0.297,

NPV(0.2) = -0.137.

In order to understand the essence of the

estimation of the project better, let's calculate the

approximate internal rate of return on the basis of

the complex percentage when the rate of return

makes: a) 10 %, b) 20 %. The obtained results are as

follow:

()

121

NPVNPV

NPV

iiiIRR

−

⋅−+=

(5)

here IRR is internal rate of return; i

is the lower rate

of discount; i

is the higher rate of discount; NPV

net present value adequate to the lower rate of

discount; NPV

is net present value adequate to the

higher rate of discount. After inserting all the

necessary values into Equation 5 the following

results have been obtained: IRR = 0.1684; (16.84

%). Having compared the approximate internal rate

of return with the actual rate we see that the

difference is rather insignificant.

2.1 The Calculation of the Logistic

Internal Rate of Return (LIRR)

The LIRR is calculated with the use of the LNVP

equation (Formula 4). It is calculated manually for a

better understanding of the essence of the relation

between the variables. By means of approximation

we find out that LIRR = 0. With the help of the MS

Excel programme the calculation sequence is as

shown in Table 2: we write the chosen K

p value in

one of the cells; in another one we write a presumed

initial value of the rate of interest i until the LNPV

becomes low enough (close to zero). In fact, the

obtained rate of interest is the LIRR value that we

wanted to know. Further on, it will be written into

Table 3.

Table 2.

K0 K1 K2 K3 K4 K5

- 1 - 0.5 0.5 0.5 0.5 1

i Kp

LNPV =

- 0.000000738711

0.700993 1.03

2.2 The Sequence of Filling in Table 3

To structure a chart of the acceptable quality it is

necessary to have at least 10-12 chart points. It

should be stressed that the curve zone of the chart is

especially significant. Here the density of the chart

points should be higher. Having this in mind, let's

select the Kp value line, recalculate the K / K

values

and write them into the next line. In our case, K = 1;

it is a member of the largest flow. The logistic

values, or the LIRR line is filled in as mentioned

before: for each K

value an i value is introduced,

which makes the LNPV to be extremely low: < 10

-4

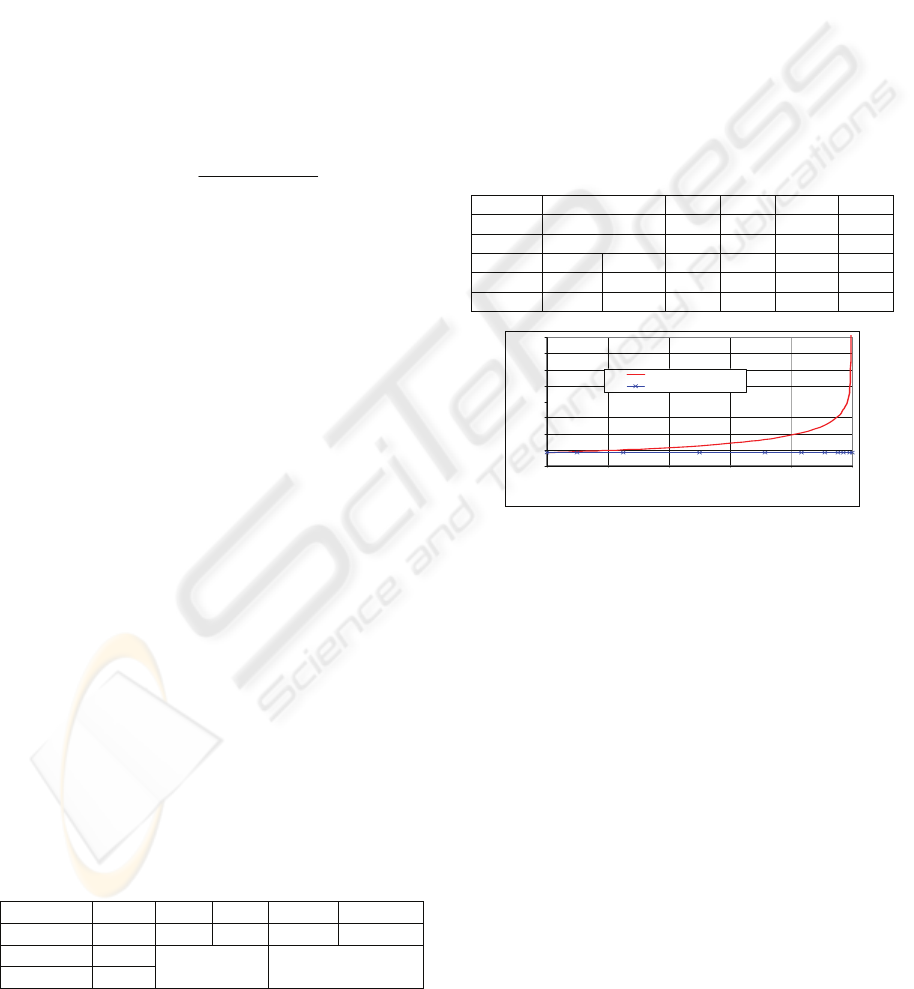
Figure 1 shows the graphical presentation of the

solution of the equations (Girdzijauskas S.,

Moskaliova V., 2005, p. 26).

Table 3.

100000 10 4 2 1.4

K/Kp

0.00001 0.1 0.25 0.5 0.71

LIRR

0.1632 0.18 0.20 0.25 0.33

1.2 1.1 1.05 1.03 1.01 1

K/Kp

0.83 0.91 0.95 0.97 0.99 1.00

LIRR

0.41 0.50 0.61 0.70 0.91 2.49

0.0

0.2

0.4

0.6

0.8

1.0

1.2

1.4

1.6

00.20.40.60.81

Market filling degree

Investment rate of return

Logistic rate of return

Normal rat e of return

Source: worked out by the authors with the data from Table 2.

Figure 1: Graph of investment heat (or of the growth of

internal rate of return).

The economic stability is strongly influenced by

the financial bubbles. The classical definition of a

financial bubble was introduced by Ch. Kindleberger

in 1978. Figure 1 clearly demonstrates that when the

investment is approaching the limit, i. e., reaching

the K

value, the threat of the bubble formation

appears (Streimikiene D., Girdzijauskas S., 2009,

2008).

The bubble is an exponentially growing increase

in price of an asset or a set of assets in a continuous

process when the initial increase in price is

determined by the vanishing decrease of the capital

niche, and the following growth of the internal rate

of return. It creates false expectations for a further

continuous growth in profitability and hence attracts

the new members of the market – in most cases,

profiteers who are interested in the profit brought by

MODELING THE FRAGILE ECONOMIC SITUATIONS

169

the asset trade rather than in the assets' capacity to

generate income.

3 CONCLUSIONS

• The possibilities for the application of the

logistic models in solving the economic

problems provide the opportunity to study the

formation of the financial bubbles.

• The practical modeling of the economic

bubbles allows to understand the assumptions

for the formation of the fragile economic

situations. Experts in economics should

improve their qualification by developing new

competences in the market estimation.

• The explored example of the logistic or

limited model should help to work out the

effective means for the prediction of the

economic situations.

REFERENCES

Girdzijauskas S. A., Streimikiene D., Dubnikovas M.,

2009. Analysing Banking Capital with Loglet Lab

Software Package. Transformations in Business &

Economics, p. 45-56.

Girdzijauskas S., Streimikiene D., et al, 2009. Formation

of Economic Bubbles: Causes and Possible

Preventions. Technological and Economic

Development of Economy, p. 267-280.

Girdzijauskas S., Streimikiene D., 2009. Application of

Logistic Models for Stock Market Bubbles Analysis.

Journal of Business Economics and Management, p.

45.

Girdzijauskas S., 2006. Logistine kapitalo valdymo teorija

: determinuotieji metodai : monografija. Vilnius.

Girdzijauskas S., Moskaliova V., 2005. Instability

modelling of financial pyramids. 5th International

Scientific and Practical Conference on Environment,

Technology, Resources, Jun 16-18, Rezekne, Latvia,

p. 26-32.

Streimikiene D., Girdzijauskas S.A., 2008. Logistic

growth models for analysis of sustainable growth.

Transformations in business & economics, p. 218-235.

Streimikiene D., Girdzijauskas S., 2009. Assessment of

post-Kyoto climate change mitigation regimes impact

on sustainable development. Renewable & sustainable

energy reviews, p. 118-130.

Girdzijauskas S., Streimikiene D., 2008. Logistic growth

models for analysis of stocks markets bubbles. World

Congress on Engineering, Imperial Coll London.

Engineering and Computer Science, p. 1166-1170.

Girdzijauskas S., Pikturna A., Ivanauskas F., et al., 2008.

Investigation of the elasticity of the price bubble

functions. 20th International Conference/Euro Mini

Conference on Continuous Optimization and

Knowledge-Based Technologies (EurOPT 2008), May

20-23, Neringa, Lithuania, p. 131-136.

Girdzijauskas S., Cepinskis J., Jurkonyte E., 2008.

Transformations in Insurance Market: Modern

Accounting Method of Insurance Tariffs.

Transformations in Business & Economics, p. 143-

153.

Girdzijauskas S.A., 2008. The Logistic Theory of Capital

Management: Deterministic Methods – Introduction.

Transformations in Business & Economics, p. 22-163

Gronskas H.Y., Streimikiene D., Girdzijauskas S.A., 2008.

Economy, Anti-economy and Globalisation.

Transformations in Business & Economics, p. 166-

168.

Merkevicius E., Garsva G., Girdzijauskas S., et al., 2007.

Predicting of Changes of Companies' Financial

Standings on the Basis of Self-organizing Maps. 9th

International Conference on Enterprise Information

Systems (ICEIS 2007), Funchal, Portugal, p. 416-419.

Moskaliova V., Girdzijauskas S., 2006. The Risk of

Investment: Determinate Models. 7th International

Baltic Conference on Databases and Information

Systems, Vilnius, Lithuania, p. 91-100.

CSEDU 2010 - 2nd International Conference on Computer Supported Education

170