
A MULTI-AGENT MODEL FOR SIMULATING THE IMPACT OF
SOCIAL STRUCTURE IN LINGUISTIC CONVERGENCE
Gemma Bel-Enguix
GRLMC, Rovira i Virgili University, Tarragona, Spain
Keywords:
Language evolution and change, Multi-agent simulation, Social structures.
Abstract:
Baronchelli (Baronchelli et al., 2006) introduced a very simple model for simulating language emergence in
communities of agents without any predetermined protocol. Brigatti (Brigatti, 2008) introduced the notion of
Reputation in Baronchellis model, demonstrating how this parameter has an impact in the final results of the
process. In a previous paper, we have shown that reputation is a key element in the coevolution of language
and social structures in societies with asymmetrically distributed reputation. This paper presents a system for
simulating linguistic convergence in static and dynamic populations with asymmetrically distributed reputation
and a graphical representation of such process.
1 INTRODUCTION
This paper investigates the relationship between so-
cial parameters and language evolution by means of
simulation of linguistic convergence. The questions
the paper address are the following: Has reputation a
crucial role in convergence time? Is there any coevo-
lution of social structures and language? Can social
structure block linguistic convergence?
To develop the topic, we use an algorithm that al-
low a community of agents to agree about naming an
object without any preestablished protocol. In this al-
gorithm we give a key role to reputation in the start-
ing of communication. Simulations with this algo-
rithm try to establish the main parameters of t
conv
,
t
max
, W
max
, W
di f
. The program gives also the output
of a graph structure that represents a social network
built up from successful linguistic interactions. These
graphs can be analysed from a mathematical point of
view.
The paper is structured as follows: in Section 2 we
introduce the main algorithm and the concepts we are
dealing with. Section 3 explains the main results ob-
tained with the model. Finally, Section 4 gives some
discussion and ideas for future research.
2 MODEL
The model is based in the one introduced by
(Baronchelli et al., 2006). Baronchelli’s model is a
variant of the naming game (Steels, 1997) and its de-
sign tries to be as simple as possible, assuming the
cognitive deficiencies this implies. In Baronchelli’s
system, a number of agents have to agree in naming
an object with no preestablished protocol. Two chief
features of the design are that: a) the agents have noth-
ing in the beginning, and b) when two agents agree in
a word, they delete everything else they have stored.
Mathematical and physical results obtained by this
model seem to show that language convergence and
evolution follow some rules that can be computation-
ally approached and simulated.
After Baronchelli’s work, Brigatti introduced the
concept of reputation in the process of linguistic con-
vergence, pointing out the possibility of analysing the
influence of such parameter in language evolution.
The present paper modifies the original model in a
way that two agents are allowed to communicate only
under several circumstances, if their reputations are
“compatible”. We start imagining a society divided in
two different social groups. Each one of this groups
has a reputation R. The group with the highest reputa-
tion is called H, and the group with the lower reputa-
tion is called L. R
H
6= R
L
and by definition R
H
> R
L
.
δ = R
H
− R
L
. δ has an important impact in the con-
vergence process, but for simplicity, in this paper, we
are using only δ20, focusing in the role some other
parameters have in the evolution.
Our system will simulate a population of 100
agents, divided into two different groups H and L, so
as |H| + |L| = 100. The way to describe a population
367
Bel-Enguix G. (2010).
A MULTI-AGENT MODEL FOR SIMULATING THE IMPACT OF SOCIAL STRUCTURE IN LINGUISTIC CONVERGENCE.
In Proceedings of the 2nd International Conference on Agents and Artificial Intelligence, pages 367-372
DOI: 10.5220/0002772703670372
Copyright
c
SciTePress

will be H%/L%. In the initial configuration agents do
not have any linguistic knowledge. The final goal is
to reach, for the whole population a common meaning
for an object M, in a way that, at the end, every agent
will have only one word stored, and this word will be
the same for every agent. The system does not stop if
such configuration is not reached.
The main protocol for every step of communica-
tion is:
i. Select randomly a speaker S. Select
randomly a hearer H, so as H 6= S.
ii. if S and H compatible, then:
- S selects a word
· case H does not have any word
stored, it invents one, W
i
.
· case H has some words stored, it
chooses one, W
i
.
- S send W
i
to H.
- if W
i
was already in H then:
· success. S and H delete
everything keeping only W
i
.
· FINISH
- else:
· failure. H stores W
i
.
· FINISH
iii. else: FINISH.
We imagine two types of societies in what refers
to protocols of communication:
• Societies where group communication is allowed.
In these societies, members of L can communi-
cate between them, and members of H can com-
municate between them. The communication is
allowed if R
S
>= R
H
.
• Societies where group communication is not al-
lowed. In these societies, it is required for com-
munication that R
S
> R
H
.
From the point of view of reputation, we consider
two different types of societies:
• Dynamic populations: those in which reputation
varies as a result of communication (Dynamic R).
• Static populations: those in which reputation does
not change (Static R).
From here, there are four main cases which are
considered in this paper:
• R
S
=> R
H
and static R (GS)
• R
S
=> R
H
and dynamic R (GD)
• R
S
> R
H
and static R (NGS)
• R
S
> R
H
and dynamic R (NGD)
In each one of these cases, the following parame-
ters will be studied:
• The convergence, or not, of the language of the
population
• t
conv
, the total time the system takes to reach the
convergence.
• W
max
, the maximum number of words the system
reaches at time t
max
• W
di f
, the maximum number of different words
• t
max
, the time where the system gets W
max
• The graph configuration.
In a precedent paper (submitted), it has been
demonstrated that some of the best results are ob-
tained in populations 20/80 and δ20. The configu-
ration used for simulations, with populations of 100
agents, takes also δ20 and the every distribution of
population from 10/90 to 90/10.
For a sake of simplicity - to get understandable
graphs - simulations with graphs have been designed
with only 20 agents and the same configuration 20/80
with δ20
3 DESCRIPTION AND
BEHAVIOUR OF THE SYSTEMS
In this section describe in more detail the structure of
every one of the classes mentioned above (GS, GD,
NGS, NGD) and explore the results with every type of
society arisen from the previous one: GS, GD, NGS,
NGD. Later, we compare this results to understand
what of the configurations is optimal, in terms of time
and space, to generate consensus words.
3.1 Systems with Static R and Group
Communication: GS Societies
These systems correspond to a population with two
different social groups where individuals of each one
of them are allowed to communicate to others in
the same group, and the individuals of L can only
hear/learn - but not speak to - individuals of H. On
the contrary, members of H speak to L, but they never
learn or listen them. However, when S and H belong
to the same group, no restrictions about the roles are
established.
To design the program to simulate such behaviour,
we take the general algorithm with a modification in
line [ii], which finally will be as follows:
ii. if R
S
>= R
H
, then:
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
368
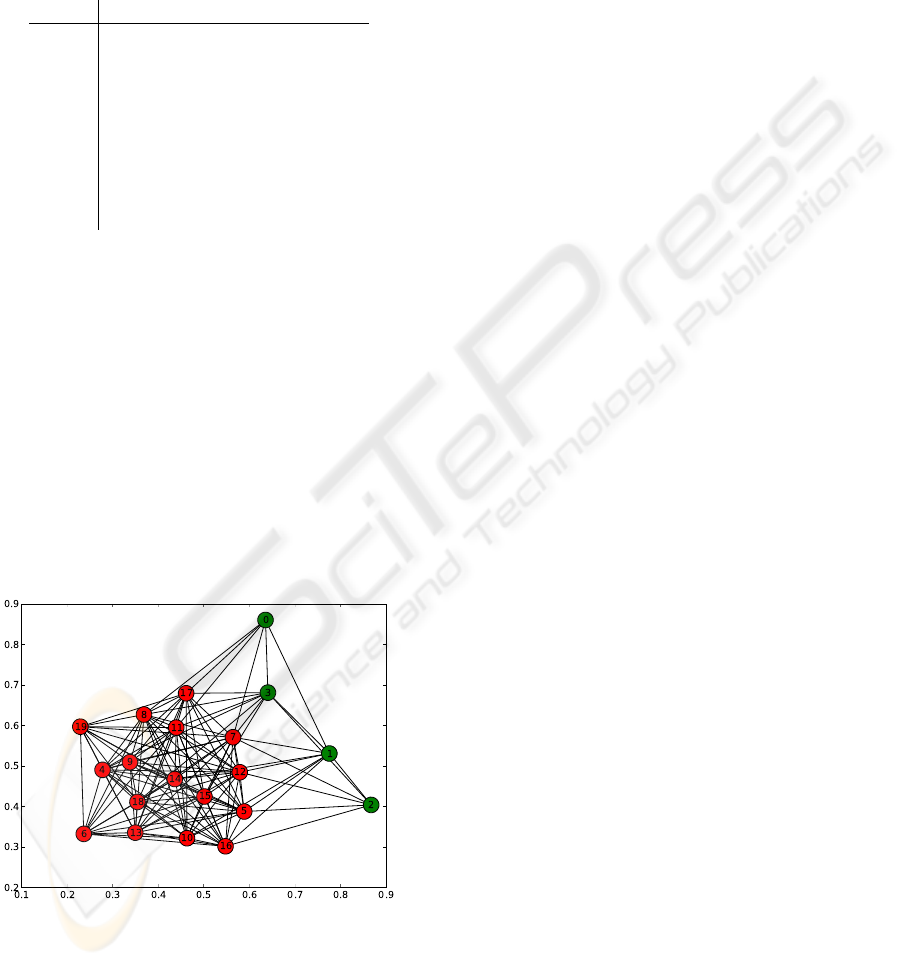
3.1.1 Results
The results with R
S
>= R
H
, R= , δ20, and different
configurations of H/L, are the following (Table 1):
Table 1: Results for populations with static R and group
communication: GS.
GS t
conv
t
max
W
max
W d
max
10/90 14435 708 398 51
20/80 5066 743 385 52
30/70 4421 753 378 51
40/60 3923 790 375 50
50/50 3678 779 367 49
60/40 3238 764 368 48
70/30 3207 753 371 47
80/20 2887 702 377 47
90/10 2680 685 389 48
Table 1 explains that, for societies in which it is
allowed to communicate between the individuals of
the same group and R does not change, the best con-
figuration for reaching a consensus language in both,
time and number of words, is 90/10. This is the opti-
mal configuration, mainly in what refers to parameter
t
conv
. Like in other societies with reputation, 10/90
has extremely bad results for δ20. However, every
parameter optimises with 90/10. Regarding to t
max
,
W
max
and W d
max
, they also have the best behaviour
with 90/10, although their improvements are smaller
than in t
conv
Such systems generate a graph similar to the one
in Figure 1.
Figure 1: Graph at t
conv
in societies with static R and group
communication: GS.
3.2 Systems with Dynamic R and Group
Communication: GD
This case refers societies where, in principle, every
type of communication is allowed. In addition, these
societies have the capacity to evolve, creating new
groups of reputation or simply not forbidding indi-
viduals to change. To obtain this systems, we need to
implement some changes in the points [ii.] and [iii.]
of the general algorithm, in order to introduce the pa-
rameter of dynamic R.
We see in the algorithm how the only reputation
that varies at each communication act is speaker’s rep-
utation, as (Brigatti, 2008) suggested in his paper.
ii. if R
S
>= R
H
, then:
- S selects a word
- S send W
i
to H.
- if W
i
was already in H then:
· success. S and H delete
everything keeping only W
i
.
· R=R+1
· FINISH
- else:
· failure. H stores W
i
.
· R=R-1
· FINISH
iii. else
· R=R-1
· FINISH
3.2.1 Results
Comparing Table 1 and Table 2 we can se how, for
t
conv
, the results in GD are more stable for every
configuration of H/L. Some variation exists, but it is
smaller. For t
conv
90/10 is still the best group distri-
bution, like in GS, but for t
max
and W
max
the tendency
is to increase the complexity with greater groups H.
The number of different words generated by the sys-
tem remains almost the same for every H/L.
Such systems generate graphs with the one in Fig-
ure 2.
3.3 Systems with Static R Without
Group Communication: NGS
Societies with static R without group communication
are not able to converge, unless the total number of
agents in H is 1. This means that, for societies with
100 agents, we need the configuration 1/99, and for
1000 agents 0.1/99.9.
A MULTI-AGENT MODEL FOR SIMULATING THE IMPACT OF SOCIAL STRUCTURE IN LINGUISTIC
CONVERGENCE
369
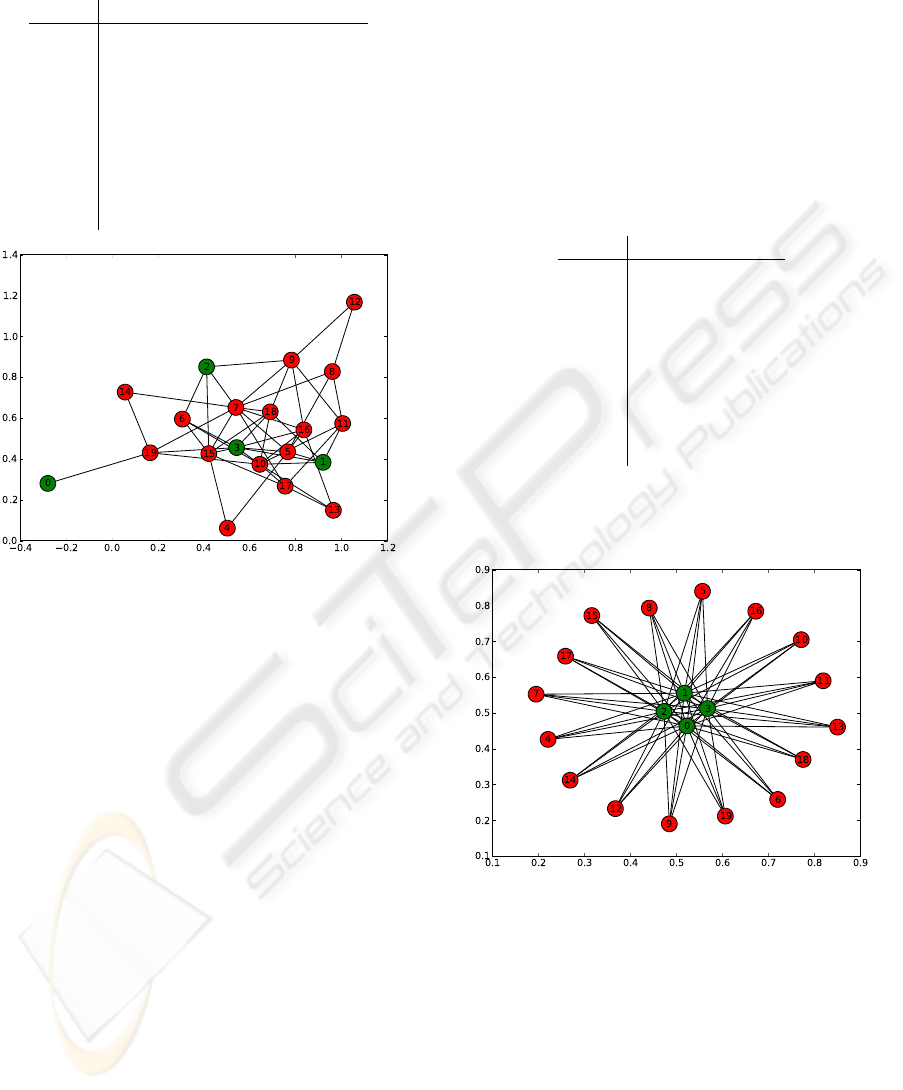
Table 2: Results for populations with dynamic R and group
communication: GD.
GD t
conv
t
max
W
max
W d
max
10/90 5320 986 400 61
20/80 5881 1024 387 59
30/70 5758 993 382 58
40/60 5121 1048 384 57
50/50 4901 1063 385 56
60/40 4935 1056 391 55
70/30 4993 1101 400 55
80/20 5049 1139 416 57
90/10 4656 1101 420 59
Figure 2: Graph at t
conv
in societies with dynamic R and
group communication: GD.
The protocol is modified from the general one in a
way that it says:
ii. if R
S
> R
H
, then:
This prevents individuals from the same group to
communicate.
3.3.1 Results
After a number of communication steps, the society
reaches a star graph. This is typically produced by
non convergent populations in which agents are only
allowed to speak with the ones with lower capacity.
So, a great part of the population cannot produce any
word. Communication with agents with the same rep-
utation is forbidden. This implies that the only possi-
ble communication is from agents in H as speakers
to agents in L as hearers. Therefore, no word gener-
ated by an individual from L can be spread. Agents
in L can never have a successful communication as a
speakers.
Provided that convergence is not possible, the pro-
gram tries to find the number of communication steps
that are necessary to reach the final stable star config-
uration t
star
, and and the number the number of words
in t
star
. The results showed in Table 3 are obtained
with only one run, so as they are only indicative. Nev-
ertheless, looking at the results for t
star
– about 100
times slower that t
conv
in GS, GD, NGD – it is easy to
see how difficult is, for such populations, to evolve.
The number of words in t
star
, W
star
is very similar to
W
max
in the other systems, what suggests that the sta-
ble configuration is achieved close to t
max
.
Table 3: Results for populations with dynamic R and group
communication: NGS.
NGS t
star
W
star
10/90 425226 259
20/80 478117 325
30/70 576348 322
40/60 787554 335
50/50 657670 301
60/40 848112 333
70/30 1024541 235
80/20 1203182 228
90/10 864363 183
The resultant star graph is found in 3. In it, ∀i ∈ H,
deg(i) = |L|, and ∀i j ∈ L, deg( j) = |H|.
Figure 3: Star society in populations with static R and non
group communication: NGS.
3.4 Systems with Dynamic R without
Group Communication: NGD
On the contrary than NGS, populations with non
group communication but with dynamic reputation,
are able to converge. The general procedure is modi-
fied as follows:
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
370
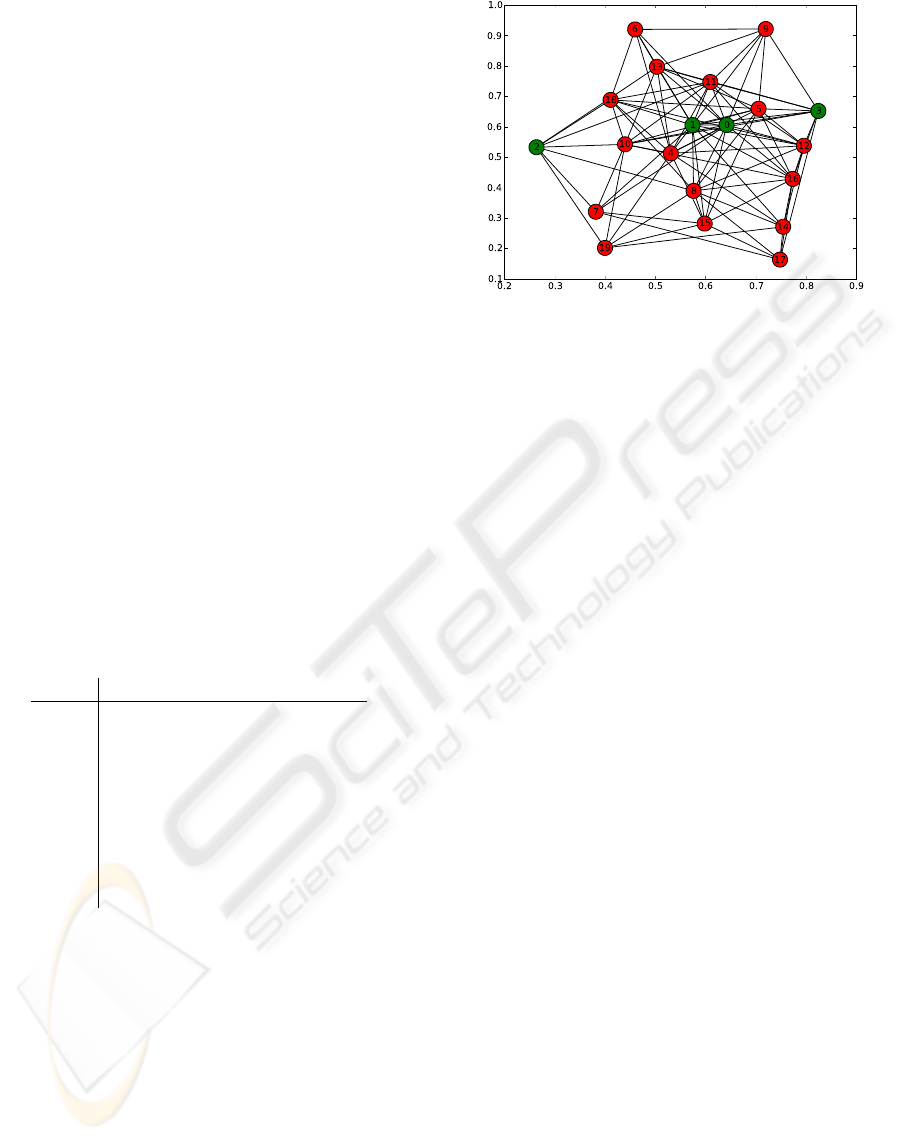
ii. if R
S
= R
H
, then:
- S selects a word
- S send W
i
to H.
- if W
i
was already in H then:
· success. S and H delete
everything keeping only W
i
.
· R=R+1
· FINISH
- else:
· failure. H stores W
i
.
· R=R-1
· FINISH
iii. else
· R=R-1
· FINISH
3.4.1 Results
Following the tendency of GD systems, NGD there is
an improvement in t
conv
from 10/90 to 90/10, but the
system is more efficient in configurations 10/90 as for
t
max
, W
max
. The number of different words seems to
increase from 10/90 to 90/10, with a central depres-
sion, centered in 40/60. This can be seen in Table 4.
Table 4: Results for populations with dynamic reputation
without group communication: NGD.
NGD t
conv
t
max
W
max
W d
max
10% 6243 1162 362 60
20% 6731 1199 360 56
30% 6372 1267 374 54
40% 6134 1302 384 55
50% 5959 1320 399 57
60% 6070 1324 410 60
70% 5956 1421 417 64
80% 5761 1455 430 67
90% 5855 1448 434 69
Figure 4 shows a graph with 20 agents generated
for NGD systems with a 20/80 distribution.
4 GENERAL RESULTS
The most important result achieved in this paper is
that populations with non-group communication and
static R (NGS) do not converge. However, they form
stable types of social structures, that slowly evolve up
to reach a star configuration that does not change. If
external factors do not apply, such societies will com-
pute for ever without any consensus, but with a strong
stable configuration.
Figure 4: Graph at t
conv
in societies with dynamic R without
group communication.
The other types of societies (GS, GD and NGD)
converge, although they have different behaviours,
that can be seen in Figure 5 for time, and Figure 6
for space (words).
Regarding convergence time (Figure 5), the results
are clear. With the exception of configuration 10/90
in GS systems, by difference the worst possible one, it
seems that GS always has better results than GD, and
GD always is faster than NGD. This means that sys-
tems with group communication obtain always better
results than societies without group communication.
On the other hand, societies with static R seem to be
faster to reach the convergence than societies with dy-
namic R. The first affirmation seems trivial and was
expected. The second one is surprising. Finally the
combination of the fastest option – static – with the
variant of non-group communication is not even able
to converge.
As for t
max
(Figure 5), the results are not so differ-
ent. The exception is that the configuration 10/90 for
GS works in a regular way.
Figure 6 shows how the results for time and space
are quite different. Regarding the maximum num-
ber of words in the system, GS and GD follow curve
distributions, with similar results in both extremes
and a depression in the center, with minimum re-
sults in balanced distributions H/L. However NGD
obtains clearly more efficient results with configura-
tions 10/90 and 20/80, and then starts increasing. As
a consequence, being NGD the configuration with the
best results for low values of H, this is he group that
needs a greater amount of words with H >= 50.
W d
max
has a similar distribution for GS and GD.
But NGD does not have the optimal results it obtained
with low values of H. Therefore, static societies with
group communication always need the lowest number
of different words to converge.
A MULTI-AGENT MODEL FOR SIMULATING THE IMPACT OF SOCIAL STRUCTURE IN LINGUISTIC
CONVERGENCE
371
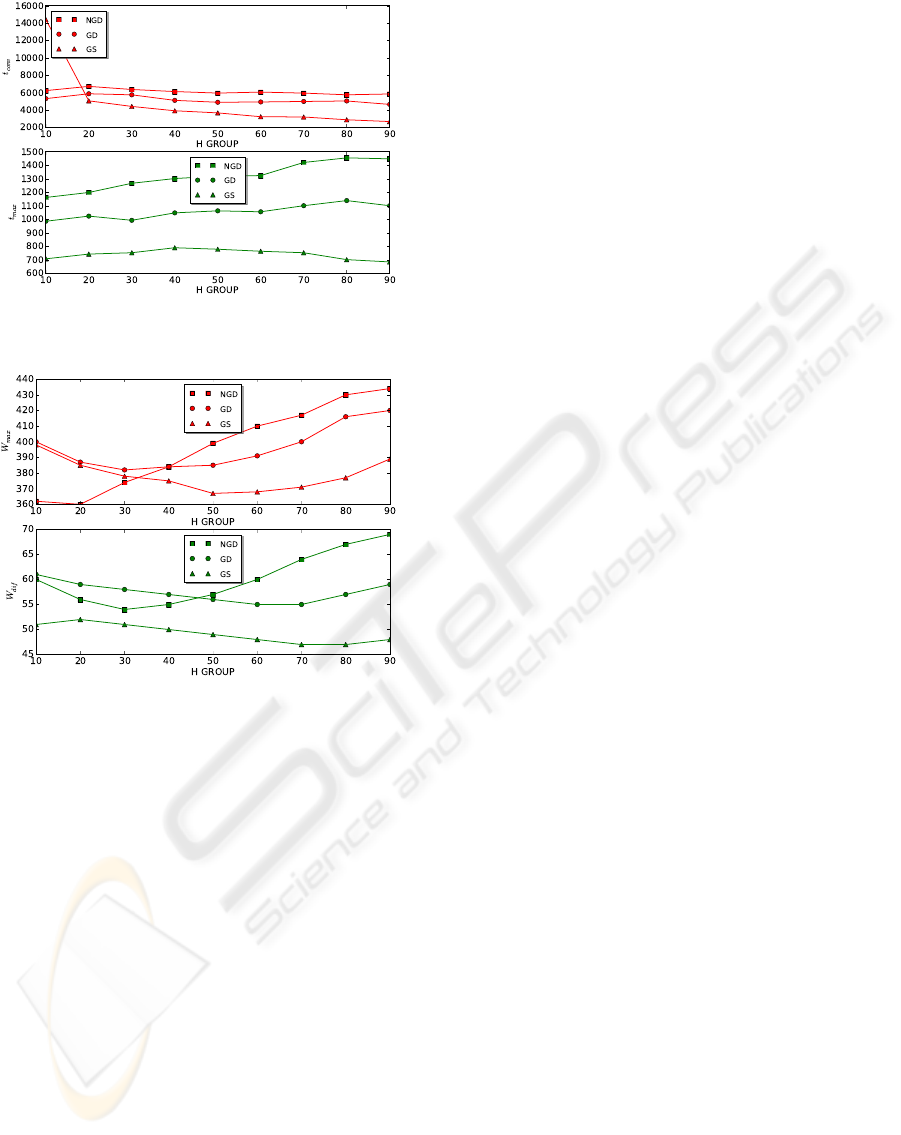
Figure 5: t
conv
and t
max
for GS, GD and NGD.
Figure 6: W
max
and W d
max
for GS, GD and NGD.
5 CONCLUSIONS
This paper is a preliminary approach with some par-
tial results about the role of dynamic/static reputa-
tion in societies, in combination with the parameter
of group communication. The first results show that
computational simulation of linguistic processes re-
lated with social issues can be very fruitful, since we
have obtained surprising results in this first approach.
Among the issues that should be investigated in
this line of research, we can remark:
a) the impact of different values of δ, since this paper
is based on simulations performed with δ20;
b) the study of the configuration of the graphs;
c) testing of the program with large populations;
d) the evolution of reputation in dynamic popula-
tions.
ACKNOWLEDGEMENTS
The author gratefully acknowledges the critical dis-
cission and inspiring ideas from Simon Kirby and the
people from LEC (University of Edinburg). This re-
search has the support from the Spanish Ministerio de
Ciencia e Innovaci
´
on in the form of a Jos
´
e Castillejo
grant JC2008-00040.
REFERENCES
Baronchelli, A., Felici, M., Caglioti, E., Loreto, V., and
Steels, L. (2006). Sharp transiton towards shared vo-
cabularies in multi-agent systemse. cze. Journal of
Stat. Mech., arXiv:physics/0509075v2.
Brigatti, E. (2008). Consequence of reputation in an open-
ended naming game. Physical Review E 78, 046108.
Steels, L. (1997). The synthetic modeling of language ori-
gins. Evolution of Communication, 1:1–34.
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
372
