CORD: A HYBRID APPROACH FOR EFFICIENT
CLUSTERING OF ORDINAL DATA USING
FUZZY LOGIC AND SELF-ORGANIZING MAPS
Natascha Hoebel and Stanislav Kreuzer
Department of Computer Science and Mathematics, Database and Information Systems
Goethe University Frankfurt, Germany
Keywords:
User profile analysis, Clustering, Ordinal data, Optimization, Web mining.
Abstract:
This paper presents CORD, a hybrid clustering system, which combines modifications of three modern clus-
tering approaches to create a hybrid solution, that is able to efficiently process very large sets of ordinal data.
The Self-organizing Maps algorithm for categorical data by Chen and Marques is hereby used for a rough pre-
clustering for finding the initial position and number of centroids. The main clustering task utilizes a k-modes
algorithm and its fuzzy set extension described by Kim et al. for categorical data using fuzzy centroids. Finally
in dealing with large amounts of data, the BIRCH algorithm described by Zhang et al. for efficient clustering
of very large databases (VLDBs) is adapted to ordinal data. BIRCH can be used as a preliminary phase for
both Fuzzy Centroids and NCSOM. Both algorithms profit from this symbiosis as their iterative computations
can be done on data, that is fully held in main memory. Combining these approaches, the resulting system
is able to extract significant information even from very large datasets efficiently. The presented reference
implementation of the hybrid system shows good results. The aim is clustering and visual analyzing large
amounts of user profiles. This should help in understanding Web user behavior and personalize advertisement.
1 INTRODUCTION
Clustering algorithms have evolved greatly since the
development of data-mining technologies in terms
of significance, as well as performance and quality.
Especially when taking into account the constantly
growing number of algorithms, research of the us-
ability and adaptivity seems inevitable in a practical
environment. It is obvious that an efficient solution
to all clustering problems cannot be concentrated into
one algorithm. Therefore it is necessary to expand
the field of research to a set of partial solutions. Some
of these solutions are adaptable to changing practical
requirements exploiting synergies of their members.
This paper introduces CORD (Clustering of
Ordinal Data), a hybrid clustering algorithm system.
Main contribution of our work presented herein is:
• Definition of a more accurate distance measure for
ordinal data (section 4.1).
• Extension of the known algorithms to work with
ordinal data by using the described measure.
• Optimization of the time complexity of Fuzzy-
Centroids (Kim et al., 2004) and showing its im-
plementation, which allows the results to be saved
and therefore refined later (section 4.2).
• Improvement of the result of the clustering task by
helping in the decision process of choosing how
many centroids should be used; and where should
the k-centroids be placed. This is possible through
our hybrid approach with NCSOM.
• Improvement of the clustering task so that it
works with very large datasets. This is possible
through our hybrid approach with BIRCH.
• Definition of the normalization for the sum of w
l,t
for FuzzyCentroids (assumption in 3.1).
1.1 Problem Formulation
Clustering of elements is a common problem and has
been broadly discussed. All algorithms have to deal
with the issue of distance computation for the ob-
served elements. Most of the known approaches fo-
cus on numerical data that allows measuring the dis-
tance by arithmetic operations, for example Euclidean
or chi-squared distance metric. Others focus on cate-
gorical data ((Gan et al., 2005), (Huang, 1997), and
297
Hoebel N. and Kreuzer S.
CORD: A HYBRID APPROACH FOR EFFICIENT CLUSTERING OF ORDINAL DATA USING FUZZY LOGIC AND SELF-ORGANIZING MAPS.
DOI: 10.5220/0002795402970306
In Proceedings of the 6th International Conference on Web Information Systems and Technology (WEBIST 2010), page
ISBN: 978-989-674-025-2
Copyright
c
 2010 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

(Parmar et al., 2007)) and measure the distance e.g.
by counting the number of different attribute values.
This is known as Hamming distance.
The focus of the CORD approach is to efficiently
cluster large amounts of ordinal data. Ordinal data,
unlike pure categorical data, possesses an inherent or-
der. Though this order can not be utilized to improve
a distance metric in general, there are specific cases,
where this kind of information can be a valuable asset
and enhance the quality of the cluster analysis.
1.2 Problem Application: User Profiles
The motivation in the design of CORD arose in the
Gugubarra project (Zicari et al., 2006). This project
lacks an appropriate solution for clustering and visual
analyzing large amounts of user profiles. The project
focuses on calculating different kinds of user profiles
of Web site visitors and understanding the user behav-
ior. The non-obvious user profiles (NOPs) represent
the interests of users in different topics. It is a vec-
tor per user with numerical values between 0 and 1
for each topic. While a numerical value is not very
meaningful, these values can be mapped to a so called
scale of interest. Sometimes these profiles are stored
in this scale, right from the start. The scale of interest
classifies the values in a human understandable form
and is ordinal. An example of a scale of interest is:
no, little, medium, high, absolute interest. Another
kind of profile is the user feedback profile. Several
Web sites allow or ask their users to give a feedback
on their interests, hobbies or opinions about a prod-
uct or the site itself. A user feedback can hereby be
given on a scale of interest over a number of topics.
The reply can then be stored in a feedback profile. To
understand users better, it can be of interest to cluster
across this feedback (i.e. what the user tells about his
interest) and the NOP (i.e. what he is supposed to be
interested in, by analyzing his click streams).
The paper shows the design and implementation
of a clustering solution in the area of clustering user
profiles and in general for clustering VLDBs of ordi-
nal data having the same cardinality and scale.
The rest of the paper is structured as follows: Sec-
tion 2 introduces the necessary definitions. Theoret-
ical foundations are presented in section 3. Section
4 describes the design and implementation of CORD.
Section 5 presents the experimental results. Related
work is compared in section 6.
2 DEFINITIONS
This section defines some of the concepts that will be
used in the rest of the paper.
Let N be the entire set of categorical records X:
N =
{
X
1
,...,X
n
}
,
|
N
|
= n (1)
with a relational schema R =
{
A
1
,...,A
r
}
with
|
R
|
= r.
A
i
, i = 1, ...,r is a categorical attribute with its do-
main D
i
= DOM (A
i
) respectively:
R =
{
A
1
,...,A
r
}
, D
i
= DOM (A
i
), i = 1, ...,r (2)
A domain D
i
for attribute A
i
is a set of categorical
values a
i, j
:
D
i
=
{
a
i,1
,...,a
i,n
i
}
, j = 1,...,n
i
(3)
A record X ∈ N is a tuple of r categorical values
x
i
∈ D
i
of the attributes A
1
,...,A
r
, that belong to the
relational schema R of N. The attribute value of X for
an attribute A
i
∈ R is defined as A
i
(X).
X = (x
1
,...,x
r
), x
i
∈ D
i
, A
i
(X) = x
i
, i = 1, ...,r (4)
The universe U = D
1
× D
2
× ... × D
r
of all valid as-
signments for records of N is defined as the Carte-
sian product of the domains D
i
of all attributes A
i
be-
longing to R of N. Based on this definition, a dis-
tance measure d (X ,Y) refers to a mapping given as:
d : U ×U −→ R, U = D
1
× D
2
× ... × D
r
that fulfills
for every two records X,Y of U the following con-
straints:
• d (X, X ) = d
0
, X ∈ U, d
0
∈ R
• d (X,Y ) > d
0
, X,Y ∈ U , X 6= Y
• d (X,Y ) = d (Y,X ), X,Y ∈ U
A Cluster partition C of N, is defined as C =

c
j
⊆ N

, j = 1,..., k where k is the number of clus-
ters and where for every two clusters c
i
,c
j
applies:
∀ c
i
,c
j
∈ C, i 6= j, c
i
∩ c
j
=
/
0. The centroid Z of a
cluster c
j
is a record, that is the best representative
for the average of all records in the cluster.
3 THEORETICAL
FOUNDATIONS
As CORD is a hybrid clustering algorithm based on
the following three algorithms, these algorithms are
first described in the next subsections in more detail.
WEBIST 2010 - 6th International Conference on Web Information Systems and Technologies
298

3.1 Fuzzy Centroids
The work done by Kim et al. describes a Fuzzy clus-
tering algorithm of categorical data using fuzzy cen-
troids (Kim et al., 2004), and is named FuzzyCen-
troids in the following. This algorithm is an exten-
sion of Fuzzy k-Modes (Huang, 1997), and needs the
number of clusters k, a-priori. The fundamental idea
of this approach is using fuzzy sets as centroids to
overcome the information loss between iterations in
Fuzzy k-Modes. The fuzzy sets allow to build on in-
formation from the previous iterations when choosing
the centroids in the current iteration. In this way the
center of a cluster can be calculated more accurately.
A fuzzy (set) centroid
e
Z is defined as follows:
e
Z = (
e
z
1
,...,
e
z
r
),
e
z
l
=
{
(a
l,1
,ω
l,1
),..., (a
l,n
l
,ω
l,n
l
)
}
(5)
with a
l,t
∈ A
l
,
|
A
l
|
= n
l
,0 ≤ ω
l,t
≤ 1 , 1 ≤ l ≤ r , 1 ≤
t ≤ n
l
and
∑
n
l
t=1
ω
l,t
= 1 , 1 ≤ l ≤ r. The values ω
l,t
build for each cluster the confidence degree matrix
W
i
= [ω
l,t
] , 1 ≤ i ≤ k. Each
e
z
l
∈
e
Z is determined by
the category distribution of attribute A
l
of the records
belonging to the cluster. ω
l,t
indicates the confidence
degree (or resonance) with which the attribute value
a
l,t
contributes to
e
z
l
.
In the first step, initial centroids are chosen by se-
lecting the values ω
l,t
. In the second step the mem-
bership matrix M, formula (6), of the values µ
i, j
are
calculated. The fuzziness modifier m and the distance
measure d

e
Z,X

=
∑
r
l=1
δ(
e
z
l
,x
l
), that takes into ac-
count the ω
l,t
are both described in (Kim et al., 2004).
µ
i, j
(t + 1) =




k
∑
l=1


d

e
Z
i
,X
j

d

e
Z
l
,X
j



1
m−1




−1
(6)
In step three, the ω
l,t
of all centroids will be updated,
using the following stop condition, i.e. as long as there
is an improvement in minimizing the function:
J
m

M,
e
Z

=
k
∑
i=1
n
∑
j=1
(µ
i, j
)
m
d

e
Z
i
,X
j

(7)
subject to
k
∑
i=1
µ
i, j
= 1 ∧ 0 <
n
∑
j=1
µ
i, j
< n (8)
In case the stop condition is not fulfilled, step two
is repeated. Otherwise it stops. For further details,
please refer to (Kim et al., 2004).
It should be noted that ω
l,t
, as defined in (Kim
et al., 2004), can have values between 0 and 1 only.
The sum of ω
l,t
for t = 1,..., n
l
has to be equal 1.
However, because the sum is taken over µ
m
i, j
it is pos-
sible that the result is higher than 1. This problem
is not mentioned in (Kim et al., 2004) and therefore
the following assumption is made: The ω
l,t
will be
normalized after the summation. Therefore, the sum
∑
n
l
t=1
ω
l,t
= 1 , 1 ≤ l ≤ r is calculated. Afterwards the
ω
l,t
, that are part of the summation, are normalized
with the result of the summation.
3.2 BIRCH
BIRCH, introduced in (Zhang et al., 1996), is a well
known clustering method for VLDBs and broadly
studied. The whole dataset is iterated once at maxi-
mum. A cluster feature tree is built as representation
of the data. Each leaf of the CF tree is a set of cluster
features (CF). A CF saves information about the cen-
troid and the amount of records in the cluster. This
summary is small enough to be held in the fast main
memory, that is allocated by BIRCH. Using this sum-
mary, the distance measurements for numerical data
(Zhang et al., 1996) can be used between cluster fea-
tures and records. In a further phase a clustering al-
gorithm can process the leaves and is therefore faster
than working on the original dataset. A cluster feature
of a cluster c
i
for numerical data is a triple CF
i
CF
i
=

N
i
,
~
LS
i
,SS
i

(9)
with N
i
, the number of records in c
i
,
~
LS
i
=
∑
~
X∈c
j
~
X, is the linear sum of the attribute values and
SS
i
=
∑
~
X∈c
j
~
X
2
the according square sum.
BIRCH is more or less an abstract instruction for
building an algorithm for VLDBs. Zhang et al. de-
scribes an implementation of this approach for nu-
merical data, using 4 distance measurements and an
agglomerative hierarchical clustering algorithm. For
further details, please refer to (Zhang et al., 1996).
3.3 NCSOM
The NCSOM algorithm (Chen and Marques, 2005)
is an extension of the Self Organized Map (SOM)
algorithm for categorical data and builds upon ar-
tificial neural networks, described by Teuvo Koho-
nen. The data structure of the NCSOM algorithm is
a two dimensional network of K neurons. The net-
work is square and the sides have all the same num-
ber of neurons. Each neuron has a randomly initial-
ized reference vector m
j
= [m
j,1
,...,m
j,r
], where r is
the number of attributes as defined in section 2. Dur-
ing the iteration, these reference vectors change dy-
namically, since they adapt to the records already pro-
CORD: A HYBRID APPROACH FOR EFFICIENT CLUSTERING OF ORDINAL DATA USING FUZZY LOGIC AND
SELF-ORGANIZING MAPS
299

cessed and likewise to their neighbor neurons. Thus a
map of reference vectors forms, whereby similar vec-
tors lie closer to each other. The algorithm demands
no knowledge of the data and is able to determine a
global optimum of the cluster partition. For further
details of NCSOM, see (Chen and Marques, 2005).
4 CORD HYBRID ALGORITHM
AND IMPLEMENTATION
(Cheu et al., 2004) describes several possibilities to
use a hybrid algorithm. The word hybrid has its origin
from the Greek language and means bundling, cross-
ing or mixture. A hybrid is the combination of two
or more different things, aimed at achieving a par-
ticular objective. In this case, a hybrid concept is
used to cluster large amounts of ordinal data. The
first phase of the concept processes the whole dataset
once to create a summary of its most distinctive fea-
tures being small enough to be held in main memory.
A modification of BIRCH (Zhang et al., 1996), de-
scribed in subsection 4.3, is used in this phase. The
clustering task of the main phase uses the BIRCH
summary as input. Therefore the algorithm in (Kim
et al., 2004) was modified as described in subsec-
tion 4.2. A preliminary data analysis phase can
be placed before the main clustering task to review
the structure of the summary and to manually opti-
mize its initialization by choosing the initial cluster
centers. The modification of the NCSOM algorithm
(Chen and Marques, 2005) is used here for creating
a similarity map, where best places for initial cluster
centers can be seen and picked visually. The results
of the main clustering phase, consisting of k matrices
[ω
l,t
] of weights for each of the k clusters, where l is
the number of attributes and t is the number of cate-
gories for the attributes, can then be stored efficiently.
Moreover, the ability to save the weight matrices cre-
ates the possibility to pause and resume the main clus-
tering task. A refinement of an already achieved result
can then be done in the same way, allowing the use of
the old result as initialization, so that the clustering
does not have to be restarted completely.
4.1 Distance Measurement
We define in the following a distance measure for
ordinal data. The motivation is as follows: The at-
tributes of the user profiles as described in subsection
1.2 have the same cardinality and scale of attribute
values. Using the scale of interest as domain, results
in comparable attributes with the same context and
symbolism, namely the user interest in different top-
ics. This data is ordinal.
The measurements for text distances are not ap-
propriate, because the label letters itself do not play
any role. The measurements for numerical data are
also not appropriate, as the ordinal data can not be
transformed to numbers. For example, if the feed-
back is given on an ordinal scale, then this data cannot
easily be transformed into numerical values, because
ordinal data only offers information of the ordering
of some elements. The distance between these ele-
ments is not defined. This is the central matter for
this research field and is discussed in statistics. For
example, Podani has discussed this issue for Braun-
Blanquet dominance (Braun-Blanquet et al., 1932):
“it is inappropriate to analyse Braun-Blanquet abu-
dance/dominance data by methods assuming that Eu-
clidean distance is meaningful” (Podani, 2005).
The measurements for categorical data could be
applied, as by the clustering algorithms CACTUS,
ROCK or STIRR. However it seams insufficient to
us, as ordinal data can offer more information (i.e. the
ordering) than simple categorical data. The attribute
values of the scale of interest are ordered and quasi
equidistant. Therefore the number of categories be-
tween two attribute values is taken into account. We
extended the distance metric to include this ordering
into the computation, see formula (10). We accept a
small error, as it is only a quasi-equidistance, but the
distance measure is more precise with these modifi-
cations rather than without them. An example: Using
Hamming distance for categorical data, the distance
between small and high is equal to the distance be-
tween small and medium. With our proposed distance
measure in formula (10), the first distance is higher
than the second, which makes sense.
The distance measure d(X ,Y ) for two records X
and Y of dataset N is given as follows:
d (X,Y ) =
r
∑
l=1
δ (x
l
,y
l
), (10)
with r is the number of attributes as defined in sec. 2
and:
δ (x
l
,y
l
) =

0, if (x
l
= y
l
)
|
Rank(x
l
) − Rank(y
l
)
|
, otherwise
(11)
Rank(x
l
) is the position of x
l
in the order of the
scale. Given the distance d (x,y) = 1 of two records
means, that only one categorical attribute value dif-
fers, and the categories are ordered next to each other.
This is the smallest distance, that two ordinal records
can have. The next upper distance is 2, thus the dis-
tance concept is discrete.
WEBIST 2010 - 6th International Conference on Web Information Systems and Technologies
300

1 g e t M a t r i x R ow (W , X ∈ N , cost ) {
2 µ = (µ
1
,...,µ
k
) ;
3
4 f o r (W
j
∈ W , j = 1, ...,k ) {
5 d
j
= g e t D i s t a n c e (W
j
, X ) ; }
6 f o r (W
j
∈ W , j = 1, ...,k ) {
7 µ[ j] = 1 / power ( d
j
/ sum ( d
j
) , 1 / ( m −1));
8 cost += µ
j
∗ g e t D i s t a n c e (W
j
, X ) ; }
9 re t u r n µ ;
10 }
Listing 1: Membership calculation of one record.
1 new F u z z y C e n t r o i d s ( k ) {
2 W 1,W 2=

W
j

, j = 1,...,k ;
3 M = [µ
x,y
] , x = 1, ...,n , j = 1,...,k ;
4 cost
1
= 0 ;
5 cost
0
= ∞ ;
6 i
N
= 0 ;
7
8 f o r (W
j
∈ W1 , j = 1,...,k ) {
9 W
j
= i n i t i a l i z e F u z z y C e n t r o i d ( j ) ; }
10 wh i l e ( ( cost
0
< cost
1
| | i
N
< 1 ) && i
N
< max )
11 {
12 cost
1
= cost
0
;
13 f o r ( X
i
∈ N , i = 1,..., n ) {
14 µ
i
= getMatrixRow (W 1 , X
i
, cost
0
) ;
15 W 2 = u p d a t e C e n t r o i d s ( µ
i
, W2 , X
i
) ; }
16 s w i t c h P l a c e s (W 1 , W2 ) ;
17 i
N
++;}
18 }
Listing 2: Implementation of modified FuzzyCen-
troids algorithm (main phase of CORD).
4.2 Optimizing FuzzyCentroids for
Implementation
The steps of FuzzyCentroids as defined in (Kim et al.,
2004) are not optimized. The time complexity is
given as O(kn(r + M)s) where M =
∑
r
l=1
n
l
is the to-
tal number of categories of all attributes. However,
for our problem of clustering very large databases, it
makes sense to have a closer look at the real runtime.
Implementing the algorithm as described by Kim et
al. would need 5 iterations through the whole dataset.
Our first aim is minimizing the iteration cycles.
For the minimization, we changed the steps of the
algorithm. The calculation of ω
l
t
and µ
i, j
requires
each an iteration through the dataset. However it
is possible to perform both steps successively for a
record. In addition the calculation of the cost function
can be done in parallel (listing 1, line 8). The modifi-
cations do not change the functionality of FuzzyCen-
troids, but decrease the computation time. As a result
the modified version of FuzzyCentroids iterates only
once through the whole dataset in the main method.
All steps are done in the for loop for each x
i
, see
listing 2, line 13. The confidence degree matrices W
l
for all clusters are saved twice in the third order ten-
sors W 1 and W 2. This allows in each iteration ac-
1 g e t D i s t a n c e ( X ∈ N , W
l
) {
2 d = 0 ;
3
4 f o r ( i = 1, ..., r ){
5 f o r ( j = 1, ..., n
i
) {
6 i f ( x
i
∈ X != a
i, j
∈ D
i
) {
7 d +=


x
i
− a
i, j


∗W
l
[i][ j]; } } }
8 r e t u r n d ;
9 }
Listing 3: New distance measure record-to-centroid.
1 u p d a t e C e n t r o i d s ( µ , W , X ∈ N ) {
2 f o r (W
j
∈ W , j = 1, ...,k ) {
3 f o r ( i = 1, ..., r , x
i
∈ X ) {
4 ω
i,x
i
+= Math . pow ( µ
j
, m) ; } }
5 re t u r n W ;
6 }
Listing 4: Confidence degree (resonance) calculation.
cessing the result from the last iteration and save the
current result. The method switchPlaces changes
the role of the tensors in-between.
The main method, shown in listing 2, executes two
more methods. The first getMatrixRow, listing 1,
computes the membership µ
j
for the current x
i
and
the cost function. This is different to (Kim et al.,
2004), where the membership matrix is computed for
all X ∈ N in one step and the cost function in another
step. The computation for membership and cost both
rely on the measurement of distance.
The getDistance method is shown in listing 3.
For our needs, the distance calculation of (Kim et al.,
2004) is modified according to the considerations in
subsection 4.1 and formula (10).
Listing 4 shows the update of centroids. The new
resonance of ω
l,t
is calculated incrementally by taking
into account the membership degrees of one record
after another. The new tensor W 2 results at the end of
an iteration. As described in section 3.1, we perform
a normalization of ω
l,t
at the end of each iteration.
4.3 Increasing Speed with BIRCH
(Chiu et al., 2001) introduces a procedure develop-
ing on BIRCH, using an hierarchical clustering algo-
rithm. It works, with the help of a distance measure
based on maximum likelihood estimation, on mixed
numerical and categorical data. As the main goal of
our work is not on building a cluster hierarchy, but on
a partition and only on ordinal data, further improve-
ments for the selection of the distance measure and
the algorithm can be realized. The distance measure-
ment described in 4.1 ensures an optimal and useful
distance concept, that can be applied here, too.
As described in 3.2, BIRCH builds the so called
cluster features. Each CF is initialized with one
CORD: A HYBRID APPROACH FOR EFFICIENT CLUSTERING OF ORDINAL DATA USING FUZZY LOGIC AND
SELF-ORGANIZING MAPS
301

record as centroid. Other records will be absorbed,
as long as they are similar in a certain distance inter-
val. The parameter T controls the distance interval
size (radius). Using the described distance measure
for ordinal values, the parameter T defines how many
attribute values can be different from the centroid of
the CF, to be still part of the sub set, represented by
the CF. Thereby the information stored for each CF is
simplified too. Contrary to (Zhang et al., 1996) only
the centroid has to be held in the memory.
If the size of the CF tree borders the provided
memory during the execution, the tree must be re-
duced. Here the T parameter is used. T is increased
and the CFs of the old tree leaves are inserted into a
new tree. Due to the larger radius, some of the CFs
of the old tree absorb other CFs in the new tree. The
tree becomes smaller and, in addition, more diffused.
This is a good side-effect, since it leads to the fact that
outliers have marginal influence on the result, as they
disappear in the crowd.
The optimal choice of the parameter T is a diffi-
cult task. In (Zhang et al., 1996) a heuristic is used, to
determine T
i+1
from the previous value T
i
, the quan-
tity of already processed records N
i
, and the size of
the whole dataset N. For our application (see 1.1), we
define and use the following alternative heuristic:
T
i+1
= 1 + T
i
+ log
2

N
N
i
T
i

(12)
This heuristic should provide some advantages:
At the beginning, when the CF tree is too big, the
lower the ratio processed records per dataset, the
more the radius increases. At the end, when the
most records are processed, the increase of the radius
should indeed flatten but still remain high enough to
ensure, that no excessive reconstruction of the CF tree
takes place. At the start T
0
= 0 and T
1
= 1.
The first phase of CORD is based on BIRCH and
shown in listing 5. CFTree is the data structure of
the CF tree and CF
i
is the current processed cluster
feature. Each record X ∈ N is first transformed into
a cluster feature with createClusterFeature, list-
ing 5, line 8. If the tree is not too big, the method
addToNode adds the new CF into the tree by finding
the correct position. If the CF tree borders the pro-
vided memory, the processing of cluster features is
paused and updateRadius is called to increase the
radius by using the heuristic, formula (12). After this
step the method rebuildCFTree adds the CF leaves
of the old tree leaves into a new tree. Afterwards the
processing continues with the next record. Finally the
set S of records, i.e. the set of CF members of all
leaves in the CF tree, is returned.
The method addToNode is shown in listing 6. A
1 S =

center (CF
1
),...,center

CF
n
S

,
2 N =
{
X
1
,...,X
n
}
3
4 b i r c h ( N ) {
5 T = 0 ;
6
7 f o r ( ∀ X ∈ N ){
8 CF
i
= c r e a t e C l u s t e r F e a t u r e ( X ) ;
9 i f ( size (CFTree) <= maxSize−size(CF
i
)) {
10 CFTree =
11 addToNode ( CFTree , CF
i
, T ) ; }
12 e l s e {
13 T = u p d a t e R a d i u s ( T ) ;
14 CFTree =
15 r e b u i l d C F T r e e ( CFTree , T ) ;
16 addToNode ( CFTree , CF
i
, T ) ; } }
17 re t u r n S = buildSummary (CFTree) ;
18 }
Listing 5: Implementation of the first phase of CORD,
based on BIRCH.
1 addToNode ( CFTree , CF , T ) {
2 node = min
z
(node|node ∈ root (CFTree), z = d(CF, node)) ;
3
4 wh i l e ( ! isLeaf ( node ) ) {
5 node = min
z
(Child|Child ∈ node,z = d(CF, Child)) ; }
6
7 i f ( size (node) < L ) {
8 f o r ( ∀ CF
i
∈ node ) {
9 i f ( d ( CF
i
, CF ) < T )
10 r e t u r n ; }
11 node . add ( CF ) ;
12 re t u r n ; }
13 e l s e {
14 M =
{
CF
i
∈ node
}
= s p l i t L e a f ( node ) ;
15 f o r ( ∀ CF
i
∈ M ∪ CF )
16 CFTree =
17 addToNode ( CFTree , CF
i
, T ) ; }
18 re t u r n CFTree ;
19 }
Listing 6: Addition of cluster feature to a CF tree
node.
CF tree node is denoted by node. In case of a leaf
node, it is composed of a set of L CFs, otherwise a
set of B CFs. First, the appropriate leaf for adding CF
is searched recursively. The CF is added taking into
account the restrictions. Therefore the distance func-
tion d checks if the CF to be inserted will be absorbed
by one of the CFs of it’s appropriate leaf. d uses the
distance measurement according to subsection 4.1.
If the appropriate leaf is full, it has to be split into
two pieces with splitLeaf. The method addToNode
is recursively executed, for each of them. If there is
no space in the leaf, the recursion continues splitting
the CF tree nodes, until a leaf is reached with enough
space. If the procedure splits the tree root into two
nodes, these nodes are carried by a new root, that is
built. Thereby tree depth grows by one level.
This implementation of BIRCH is used for the
first phase of CORD. In the main phase, the result
from BIRCH is clustered by the modified FuzzyCen-
WEBIST 2010 - 6th International Conference on Web Information Systems and Technologies
302

troids described in 4.2. The result from BIRCH can
also be processed by a phase in-between, as described
in the following section. This new phase is used to in-
crease quality by finding adequate initial centroids.
4.4 Increasing Quality with NCSOM
Before the dataset summary from BIRCH can be clus-
tered by FuzzyCentroids, the number k of centroids
and their values have to be selected. This phase is cru-
cial for the quality of the final result. For this issue the
NCSOM algorithm can help by discovering the clus-
tering structure, which is visualized as follows: The
NCSOM forms a map of reference vectors, whereby
similar vectors lie closer to each other, as described
in section 3.3. The distance between two neighboring
vectors can be illustrated on a color palette of gray
tones. For small distances bright colors are used and
with increasing distance darker colors. A similarity
map of the data builds up as shown in figure 1. Groups
of similar neurons can be identified as bright areas on
the similarity map. If the users then selects a neu-
ron from the center on this bright area, this reference
vector will be a quite good choice as centroid of the
records represented by this area. This representation
is thus not only an assistance for finding the number
of centroids, that exist in the clustering structure. It
can additionally help very well to specify the initial
centroids allocation for a following cluster analysis.
We modified the distance measure of NCSOM, to
use it with ordinal data only, see formula (13) and
(14). The modifications are done accordingly to 4.1.
d (X
i
,m
j
) =
r
∑
l=1
δ

x
i,l
,m
j,l

, (13)
with
δ (x
i,l
,m
j,l
) =

0, if (x
i,l
= m
j,l
)
|
x
i,l
− m
j,l
|
, otherwise
(14)
The implementation of NCSOM is shown in listing 7.
Parameter δ (t) gives a monotonically decreasing ra-
dius and s
i
the vector space coordinates of the neuron
in the network. This leads to a fast move of the neu-
rons to their approximate place. In the further process
they adapt slightly until they arrive in their final place.
A good choice of δ(t) is the diagonal network length.
Step 1 of NCSOM is implemented in line 2 and
3, listing 7. initializeDelta initializes the param-
eter δ(t) and initializeArtificialNetwork the
reference vectors randomly. The data structure of
the p × p neuron network is a matrix M
p×p
= [m
i, j
].
ref (m
i, j
) is the reference vector of the respective neu-
ron, pos (m
i, j
) the vector of it’s position in the net-
work. nsum (m
i, j
) contains in each case a matrix
V
r×n
r
= [v
s,t
] for s = 1, ..., r attributes and t = 1, ..., n
r
Figure 1: Similarity map (left) and a reference vector m
j
of
one neuron (right).
1 NCSOM( size , maxIterations ) {
2 δ
t
= i n i t i a l i z e D e l t a ( size , maxIterations ) ;
3 i n i t i a l i z e A r t i f i c i a l N e t w o r k ( M , size ) ;
4
5 wh i l e ( δt >0){
6 f o r ( X
l
∈ N , l = 1,...,n ) {
7 m
i, j
= f i n d B e s t M a t c h i n g U n i t ( M , X
l
) ;
8 sa v eNeighbo u r S u m s ( X
l
, m
i, j
, M , δ
t
) ; }
9 f o r ( i = 1, ..., p , j = 1, ..., p ) {
10 b a t c h U p d a t e U n i t ( m
i, j
) ; }
11 δ
t
−−;}
12 }
Listing 7: Implementation of the second phase of
CORD, based on NCSOM.
categories. This matrix saves the summations that are
used in step 3 (see below).
The distance measurement is used during the se-
lection of the best matching neuron (Step 2). The best
matching neuron for a record is searched in each iter-
ation with the method findBestMatchingUnit, line
7, listing 7. This is the neuron with the reference vec-
tor that has the smallest distance to the record accord-
ing to formula (13) and (14). The implementation of
the distance measurement is shown in listing 8. Af-
ter the winner neuron is found, the necessary infor-
mation for the update, has to be collected. Listing 9
shows the calculation of the matrices V
r×n
r
= [v
s,t
].
This computes the occurrence frequency of the cate-
gorical values for the r attributes of the neighborhood
records, using the Gaussian function defined in (Chen
and Marques, 2005). The computational complexity
of this step is O

n
2

, as for each record and neuron a
matrix of sums has to be processed.
The update of the reference vectors (Step 3) is
1 g e t D i s t a n c e ( X ∈ N , m
i, j
) {
2 d = 0 ;
3 f o r ( i = 1, ..., r ){
4 f o r ( j = 1, ..., n
i
) {
5 i f ( x
i
∈ X != a
i
j
∈ D
i
) {
6 d +=



x
i
− a
i
j



; } } }
7 re t u r n d ;
8 }
Listing 8: New distance measure between record an
neuron.
CORD: A HYBRID APPROACH FOR EFFICIENT CLUSTERING OF ORDINAL DATA USING FUZZY LOGIC AND
SELF-ORGANIZING MAPS
303

done in line 9 to 10, listing 7, at the end of each it-
eration. The details of the implementation is shown
in listing 10. The neurons are updated according to
formula 15 and 17 in (Chen and Marques, 2005). The
summations are used in line 5. This update requires
one iteration through the whole dataset. This is rele-
vant in the case of VLDBs, as the computation time is
linear in O(maxIterations ∗ n) on the dataset size n.
An important factor is the network size. The cal-
culation in listing 9 and 10 respectively is quadratic
(O

p
2

) on the neuron number p of one side. Sum-
marizing, the best case computation time is approxi-
mately at least maxIterations ∗ n, as the algorithm al-
ways executes the maximum number of steps. This
is necessary, since the number of steps is attached to
the function δ
t
. However, also in this case, the dataset
must be read only once per iteration. This batch algo-
rithm has a better accuracy than an online algorithm
but requires memory for an additional data structure;
the matrix V
r×n
r
for the neurons.
5 EXPERIMENTAL RESULTS
To evaluate CORD, we performed tests with two dif-
ferent datasets. Subsection 5.1 describes the tests with
a dataset of 100,000 records and 5.2 the tests with 14
million records. As with work of this nature, i.e a
hybrid approach, a comparison is difficult, especially
as the proposed solution is tailored to suit a specific
use case. In our solution, the three phases of CORD
as described in section 4 can be processed indepen-
dently. For example one can select an automatic so-
lution without using NCSOM in-between. Therefore
we decided to evaluate each one separately.
In general algorithms are dependent on the read-
1 s a v e N e i g h b o u r S u ms ( X ∈ N , m
z
, M , δ
t
) {
2 f o r ( k = 1,..., p , l = 1, ..., p ) {
3 f o r ( i = 1, ..., r ){
4 f o r ( j = 1,..., n
i
) {
5 nsum

m
k,l

[i][x
i
] +=
6 exp

−


pos

m
k,l

− pos (m)


2
/2δ
2
t

;}}}
7 }
Listing 9: Calculation of categorical value frequency
of the records in the neighborhood.
1 b a t c h U p d a t e U n i t ( m ) {
2 f o r ( i = 1, ..., r ){
3 do u b l e s = 0 . 0 ;
4 f o r ( j = 1, ..., n
i
) {
5 s += j ∗nsum (m) / sum ( nsum (m) [k] ) ; }
6 ref (m) [k] = ro u n d ( s ) ; }
7 }
Listing 10: Update of the neuron reference vector at
the end of each iteration.
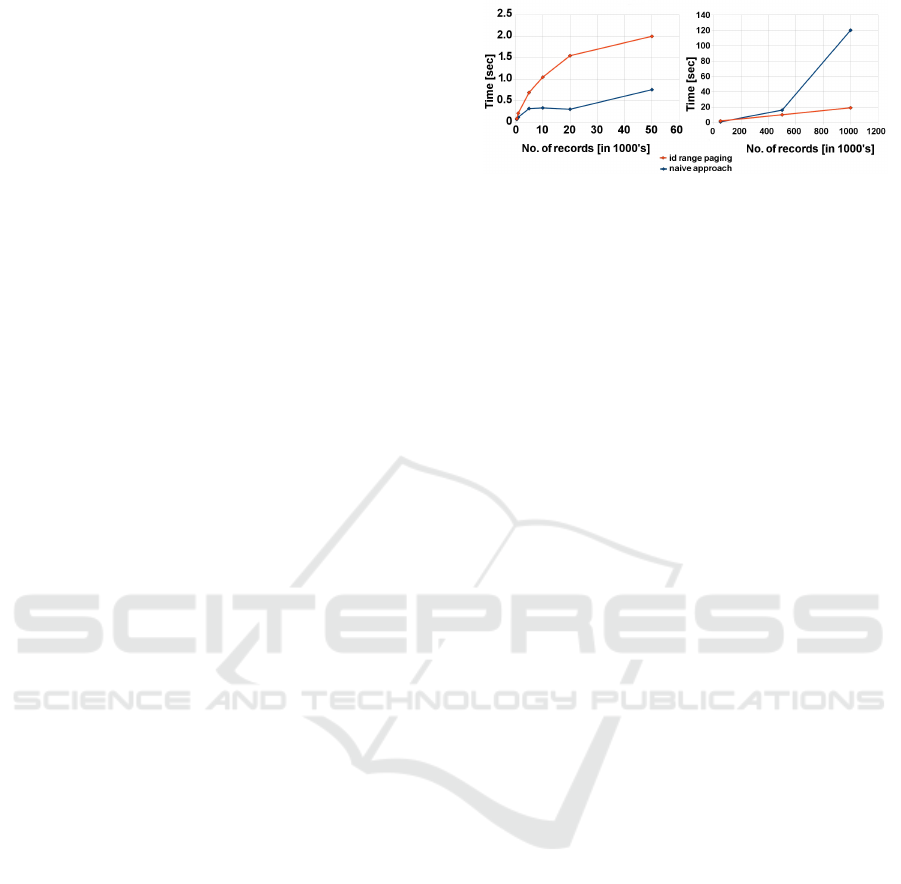
Figure 2: Reading time for naive approach and paging. Re-
sults for small record no. (left) and large data sets (right).
ing time of the data. Therefore we performed an opti-
mization of the reading process, we named as id range
paging (results shown in figure 2). A data base query
loads intervals of records (as page) on the basis of the
primary key from the data base.
The id range paging processes approximately 50
records in one millisecond. It is clearly observable,
that the id range paging exceeds the naive approach,
for which an out-of-memory exception occurred after
2 minutes and one million records. Further we tested
the influence of different page sizes on the reading
time. The size of 500 provided the best results.
5.1 Dataset User Profiles
Input for the test was a dataset of approx. 100,000
records (Gugubarra, 2009) according to the problem
application user profiles (see 1.2). The test was done
on a PC with Intel Core 2 Duo T7500 processor with
2.20GHz and 2GB DDR2 SDRAM main memory.
The module for the FuzzyCentroids was tested
with the result of BIRCH as input. Therefore the CF
tree is held in the main memory and the FuzzyCen-
troids can be executed quite fast. The computation
time depends linearly on the number of attributes.
The average of three test runs is shown in figure 3(b)
for 10, 15, 20, and 100 attributes and 1,000 records.
The number 100 is normally not exceeded for the
described user profiles (see subsection 1.2) and
supports the regression line built out of the results
for the other attribute numbers. For 100 attributes the
computation time was 150 milliseconds. Similarly
are the results for the number of records. The
computation time depends linearly on it as shown
in figure 3(a) for 1,000, 2,000, 3,000 and 105,691
records and 10 attributes. For 105,691 records the
computation time was about 2 seconds and supports
the regression line that is shown.
For testing the computation time of the BIRCH
module, we focused on the most interesting criteria.
This is when the CF tree is too big for the main mem-
ory. At this point the CF tree has to be rebuilt which
WEBIST 2010 - 6th International Conference on Web Information Systems and Technologies
304

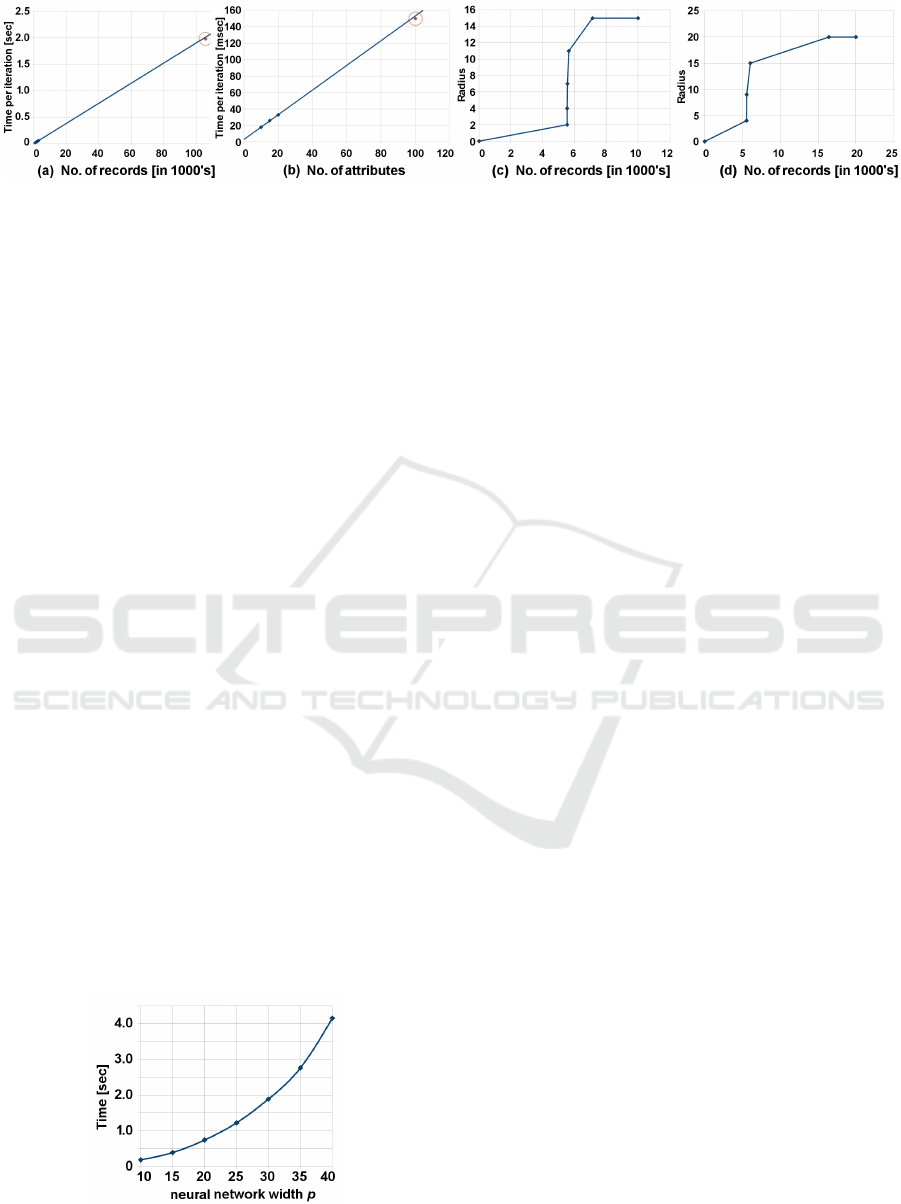
Figure 3: FuzzyCentroids evaluation for number of records (a) and attributes (b). BIRCH evaluation: Increase in the radius
for 10000 records (c) and 20000 records (d).
takes the most time. In order to ensure, that no exces-
sive reconstruction of the CF tree takes place we pro-
posed a heuristic in 4.3. It’s functionality was proven
empirically by repeated runs of the module for differ-
ent number of records and CF tree parameters. The
average of 3 test runs is shown in figure 3(c),(d) for
10,000 and 20,000 records.
The parameters were set as follows: The maxi-
mum no. of nodes as 5, maximum no. of CFs in one
leaf as 15, and the maximum size of the CF tree was
5,000,000 bytes. The result shows that at the end,
when the most records are processed, the increase in
the radius is less. Most important, the steps are big
enough to ensure a fast inclusion of the whole data
set into the CF tree. That is for 20,000 records after
5 enlargements only. It is not a perfect logarithmic
function, because the dataset used is uniform.
Similar to the FuzzyCentroids, the computation
time of NCSOM depends linearly on the number of
records and attributes. A more interesting evaluation
would be regarding the influence of the neural net-
work size, that we report here instead. The time com-
plexity is quadratic. The average of three test runs
is shown in figure 4 for 1,000 records with different
network sizes. The quadratic dependency is clearly
observable. Further the running time depends on the
number of neighbor neurons used for the computation
of the similarity map. Since this computation is im-
plemented at the end of each iteration and not for each
record, the effect is small compared with other steps.
Figure 4: NCSOM evaluation for neural network size.
5.2 Dataset MSNBC.COM Web Data
The second performance test was done to prove the
scalability of the system. It was done on a Windows
Server with two Intel Xeon E5420 processors with
2.50GHz and 8GB main memory.
The dataset MSNBC.COM Data Set was taken
from the UCI ML Repository (D.J. Newman, 2007).
The data comes from the Server logs for msnbc.com
and news-related portions of msn.com. Each se-
quence in the dataset corresponds to page views of
a user during one day. Each event in the sequence
corresponds to a user’s page request. Requests are not
recorded at the page level but rather, they are recorded
at the level of page topics. The fourteen topics we
used are “frontpage”, “news”, “tech”, “local”, “opin-
ion”, “on-air”, “misc”, “weather”, “health”, “living”,
“business”, “sports”, “summary”, and “bbs”. The full
dataset consists of approx. one million users (i.e.
989,818).
This data is very useful, as it represents click-
streams associated to topics. From this data, it is very
easy to generate profiles that are similar to the NOPs
like described in subsection 1.2. We mapped the num-
ber of page visits on an ordinal scale, representing
which topics the user has more or less “touched”.
In the Gugubarra Project the number of topics (at-
tributes) changes dynamically. Therefore each at-
tribute value is saved in a separate record. For the
dataset MSNBC.COM we chose the same domain
specific database schema to have a realistic and com-
parable situation. As a result, CORD had to work on
attribute × user records, that is 14 million records.
The average of 3 test runs for FuzzyCentroids us-
ing BIRCH was a computation time of approx. 3,300
seconds. This is a good result compared with (Kim
et al., 2004). The average of 3 test runs for NCSOM
using BIRCH was a computation of approx. 3,400
seconds. The tree size decreased from 9,200 KBytes
to 1,800 KBytes, when the radius increased to 3. The
results are similar because each of the tests had to read
the records from the database. This was the slowest
part as a lot of disk reads had to be done.
CORD: A HYBRID APPROACH FOR EFFICIENT CLUSTERING OF ORDINAL DATA USING FUZZY LOGIC AND
SELF-ORGANIZING MAPS
305

6 RELATED WORK
In the area of clustering Web users, it is a new ap-
proach to take into account the non-obvious profiles,
described in (Zicari et al., 2006). Clustering non-
obvious-profiles with CORD takes indirectly into ac-
count the time spent by the user on a page and the con-
tent topics of this page. CORD clusters users based
on their supposed interest in these topics. With the
fuzzy centroids, it gives an interpretation to the clus-
ters as a value of a predefined scale of interest. This is
a nameable advantage. Several algorithms have been
proposed in the area of clustering large datasets, as
BIRCH (Zhang et al., 1996) and CLARANS (Cluster-
ing Large Applications based on RANdom Search) by
Ng and Han (Ng and Han, 1994). There are special-
ized fields, e.g. multi-relational data clustering. Yin
and Han proposed here CrossClus (Yin et al., 2007),
that clusters data stored in multiple relational tables
based on user guidance and multi-relational features.
This algorithm requires as CORD the help of the
user, that is here the person who wants to cluster
the elements. Clustering can be applied to various
domains and issues, e.g. in (Aggarwal et al., 2006)
the k-anonymity (a technique to preserve privacy in
data) is treated as a special clustering problem, called
r-cellular clustering. (Aggarwal et al., 2006) han-
dle categorical attributes by the representation as n
equidistant points in a metric space. Hybrid Systems
are used in various research fields, e.g. in the area of
Web Burke (Burke, 2002) has defined Hybrid Recom-
mender Systems, that combine information filtering
and collaborative filtering techniques. Helmer pro-
posed in (Helmer, 2007) a hybrid approach to mea-
sure the similarity of semistructured documents based
on entropy. (Kossmann et al., 2002) use a hybrid
approach to find the Skyline, i.e. a set of interesting
points from a potentially large set of data.
REFERENCES
Aggarwal, G., Feder, T., and Kenthapadi, K. (2006).
Achieving anonymity via clustering. In Proc. of the
25
th
ACM SIGMOD-SIGACT-SIGART symposium on
Principles of database systems, pages 153–162, NY,
USA.
Braun-Blanquet, J., Conard, H. S., and Fuller, G. D. (1932).
Plant sociology. McGraw-Hill book company.
http://www.biodiversitylibrary.org/bibliography/7161.
Burke, R. (2002). Hybrid recommender systems: Survey
and experiments. User Modeling and User-Adapted
Interaction, 12(4):331–370.
Chen, N. and Marques, N. C. (2005). An extension of self-
organizing maps to categorical data. In EPIA, Portu-
gal.
Cheu, E. Y., Kwoh, C. K., and Zhou, Z. (2004). On the
two-level hybrid clustering algorithm. Nanyang Tech-
nological University.
Chiu, T., Fang, D., Chen, J., Wang, Y., and Jeris, C. (2001).
A robust and scalable clustering algorithm for mixed
type attributes in large database environment. In Pro-
ceedings of the 7
th
ACM SIGKDD, pages 263–268,
NY, USA.
D.J. Newman, A. A. (2007). UCI machine learning reposi-
tory. http://archive.ics.uci.edu/ml/.
Gan, G., Yang, Z., and Wu, J. (2005). A genetic k-modes
algorithm for clustering categorical data. In ADMA,
pages 195–202.
Gugubarra (2009). Data set user profiles. www.dbis.cs.uni-
frankfurt.de/downloads/research/data.zip.
Helmer, S. (2007). Measuring the structural similarity of
semistructured documents using entropy. In Proc. of
the 33
rd
Int. Conf. on VLDBs, pages 1022–1032.
Huang, Z. (1997). A fast clustering algorithm to cluster
very large categorical data sets in data mining. In In
Research Issues on Data Mining and Knowledge Dis-
covery, pages 1–8.
Kim, D.-W., Lee, K. H., and Lee, D. (2004). Fuzzy cluster-
ing of categorical data using fuzzy centroids. Pattern
Recogn. Lett., 25(11):1263–1271.
Kossmann, D., Ramsak, F., and Rost, S. (2002). Shoot-
ing stars in the sky: an online algorithm for skyline
queries. In Proc. of the 28
th
Int. Conf. on VLDBs,
pages 275–286.
Ng, R. T. and Han, J. (1994). Efficient and effective clus-
tering methods for spatial data mining. In Proc. of the
20
th
Int. Conf. on VLDBs, pages 144–155, San Fran-
cisco, CA, USA. Morgan Kaufmann Pub. Inc.
Parmar, D., Wu, T., and Blackhurst, J. (2007). Mmr: An
algorithm for clustering categorical data using rough
set theory.
Podani, J. (2005). Multivariate exploratory analysis of ordi-
nal data in ecology: Pitfalls, problems and solutions.
Journal of Vegetation Science, 16(5):497–510.
Yin, X., Han, J., and Yu, P. S. (2007). Crossclus: user-
guided multi-relational clustering. Data Min. Knowl.
Discov., 15(3):321–348.
Zhang, T., Ramakrishnan, R., and Livny, M. (1996). Birch:
An efficient data clustering method for vldbs. In
Proc. of the ACM SIGMOD, pages 103–114, Mon-
treal, Canada.
Zicari, R. V., Hoebel, N., Kaufmann, S., and Tolle, K.
(2006). The design of gugubarra 2.0: A tool for build-
ing and managing profiles of web users. In Proc. of the
IEEE/WIC/ACM Int. Conf. on Web Intelligence, pages
317–320, Washington, DC, USA.
WEBIST 2010 - 6th International Conference on Web Information Systems and Technologies
306