NORMAL SYNTHESIS ON RGBN IMAGES

Thiago Pereira and Luiz Velho

Vision and Graphics Laboratory, Instituto de Matematica Pura e Aplicada, Brazil

Keywords:

RGBN, Texture synthesis, Normal map, Filtering.

Abstract:

In this work, we synthesize normals and color to add geometric details to an RGBN image (image with a

color and a normal channel). Existing modeling and image processing tools are not apt to edit RGBN images

directly. Since high resolution RGBN images can be obtained using photometric stereo, we used them as full

models and as exemplars in a Texture from Example synthesis.

Our method works on RGBN images by combining the normals from two bands: base shape and details. We

use a high pass ﬁlter to extract a texture exemplar, which is synthesized over the model’s smooth normals,

taking into account foreshortening corrections. We also discuss conditions on the exemplars and models that

guarantee that the resulting normal image is a realizable surface.

1 INTRODUCTION

We use texture synthesis to edit large regions of an

RGBN image changing both color and normals. The

RGBN image (Toler-Franklin et al., 2007) is a 2.5D

data type since it is a photo containing, for each pixel,

not only color but also geometry information (nor-

mal). Editing regions by individually addressing local

changes can be painstaking to artists. For this reason

this process needs to be made automatic. Two options

arise. Procedural methods are very powerful but are

in general difﬁcult to control. We use a texture from

example method that takes as input only a small sam-

ple of the desired texture and then reproduces it in a

large region. Our system can synthesize normal tex-

tures on shapes represented by normals (RGBN im-

ages), never using positions. Regarding synthesis, an

advantage of working with RGBN images is that the

projective mapping distortions on the synthesized tex-

tures can be corrected by using information from the

normals. The texture sticks to the surface.

However, we do not want the texture to follow

every small surface irregularity. Therefore, we sep-

arate the RGBN image into macro and mesostructure

bands. It is common to cluster different geometric

scales in different levels (Chen et al., 2006). The

macrostructure level is the general shape of the model

as would be seen from a distance. The mesostructure

level contains intermediate geometric details that are

visible with a naked eye such as bumps and creases.

Our synthesis method can respect the base shape, only

changing the details.

Our method can be applied to RGBN images from

many different sources. A high-resolution modeled

mesh can be used to extract it and enhance models

with fewer polygons (Cohen et al., 1998; Cignoni

et al., 1998). Further processing of details of this

model can proceed using the normal map and avoid-

ing a huge mesh. An alternative to modelling is cap-

turing real-world objects. Capturing normals with 3D

scanning requires expensive equipment and lacks res-

olution, being far behind the cheaper digital cameras.

Better results come from photometric approaches as

in the digitization of Michelangelo’s Pieta (Bernardini

et al., 2002). A projective atlas (Velho and Sossai Jr.,

2007) can be built from this dataset. The resulting

charts are surfaces mapped by a camera transforma-

tion to the image plane. Since they contain normal

and colors, each chart is in fact an RGBN and can be

edited by our system.

Capturing a model’s normals is easy using photo-

metric stereo techniques (Woodham, 1989). It takes

as input multiple images from the same view point,

each illuminated with different known light positions.

It then solves a least-squares problem to ﬁnd the nor-

mal and albedo (color) of each pixel in the image.

Since photometric stereo works on regular images,

it allows the capture of very high resolution models.

This is a powerful method to obtain full models but

also to generate texture exemplars.

Our main contributions are:

1. Synthesizing normal vectors allowing relighting

Pereira T. and Velho L. (2010).

NORMAL SYNTHESIS ON RGBN IMAGES.

In Proceedings of the International Conference on Computer Graphics Theory and Applications, pages 13-20

DOI: 10.5220/0002813800130020

 SciTePress

Figure 1: Overview of the method. Inputs: a) RGBN image, c) texture exemplar. Filtered inputs: b) smooth RGBN image, d)

texture detail. Results: e) color, f) normal (represented in RGB colors) and g) shaded RGBN image.

of the ﬁnal model.

2. An RGBN image editing system implementing a

frequency aware texture synthesis framework sep-

arating exemplars and models into base shape and

details.

In section 3, we present an overview of our nor-

mal synthesis framework. In section 4, we discuss

the work of (Zelinka et al., 2005) in color synthesis on

RGBN images. In section 5, we extend their method

for synthesizing normals. In section 6, we determine

when the edited RGBN images correspond to a real-

izable surface.

2 RELATED WORK

Texture from example synthesis can be classiﬁed into

two approaches. In pixel-based methods, new pix-

els are generated one at a time. In (Efros and Leung,

1999), the authors search for a best match between

the neighborhood of the already synthesized texture

and neighborhoods in the texture sample. There are

also patch-based methods (Efros and Freeman, 2001)

(Fang and Hart, 2004) where the algorithm step con-

sists of iteratively synthesizing small regions at a

time. This approach leads to a direct transfer of local

statistics, but it has the drawback that seams between

patches need to be handled.

Another classiﬁcation of synthesis regards the do-

main. Texture synthesis can be parametric, volume-

based or manifold-based. Volume-based methods will

synthesize texture usually in R

or R

. Parametric

synthesis will target more general manifolds by work-

ing in the parametric domain (usually planar). There

are also manifold methods which are non-parametric

(Wei and Levoy, 2001) (Turk, 2001). These methods

work directly in the manifold representation (usually

a mesh) and use only local decisions.

In (Zelinka et al., 2005; Fang and Hart, 2004)

the authors extend manifold techniques to work on

RGBN images, using the normal as a local descrip-

tor of shape. Both works use shape from shading

to recover normals from photographs. Normals are

used to guide distortions in the synthesized color tex-

ture. Zelinka (Zelinka et al., 2005) adapted jump map

based synthesis which is a pixel based method to work

on normals, while Textureshop(Fang and Hart, 2004)

uses a patch based method. Both works allow for ad-

vanced editing of images. For example, object mate-

rial can be replaced, while still respecting shape and

shading. Unlike these works, in our method, both

color and normals are synthesized on RGBN images.

One way of looking at RGBN synthesis is as a quasi-

stationary process (Zhang et al., 2003). Synthesis pro-

ceeds through the image but varies spatially depend-

ing on the normals.

In (Haro et al., 2001), the authors capture high res-

olution normals of small patches of face skin and then

use texture synthesis to replicate these tangent space

normals in parametric space. Adding detail to faces

is an important application of our method. While

in their approach, a normal map is synthesized from

scratch, we can respect existing frequency bands in

the normal map. Procedural synthesis was explored

in (Kautz et al., 2001) where bump maps are created

on the ﬂy based on a normal density function.

(a) Original Exemplar (b) Filtered Exemplar

Figure 2: Removing the normal low frequencies of the ex-

emplar only the desired details. We show shaded images of

the normals under same lighting conditions.

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

3 METHOD

While the problem of synthesizing color textures on

top of RGBN models has been studied in (Zelinka

et al., 2005), we propose a method to synthesize nor-

mal textures. We start this section with an overview

of our method (Figure 1). The method receives as

input an RGBN image (a) and an RGBN examplar

(c). It has three steps. First, in the frequency split-

ting step, we low-pass ﬁlter the normal image (b) re-

moving details and we high-pass ﬁlter the examplar

normals (d) removing the base shape. Second, in the

texture synthesis step, we synthesize both the colors

(e) and normals (f) of the examplar on the smooth nor-

mals (b) compensating for foreshortening distortions.

Finally, in the combination step, we merge the synthe-

sized normal details with the smooth RGBN image.

To build the smooth normals we use the RGBN

bilateral ﬁlter (Toler-Franklin et al., 2007). It takes

into account both normal and color differences and

respects edges. In (Pereira and Velho, 2009), the au-

thors have developed linear ﬁlters for normals that al-

lows any kernel mask to be used. It builds on the one

to one mapping between a normal ﬁeld N(x, y) and the

gradient ﬁeld (z

, z

) of an associated height function

z given by:

N(x,y) =

(−z

, −z

, 1)

+ z

+ 1

To ﬁlter normals, they ﬁrst convert it to a height

gradient. By noting that derivatives and convolution

(g kernel) commute, the gradients can be ﬁltered as if

we had the height function z at hand.

(z ∗g)

∂(z ∗g)

∂x

∂z

∂x

∗ g = (z

∗ g)

During splitting, we use their high pass kernel on

the texture sample (Figure 2). As an alternative to

the bilateral ﬁlter we could build the smooth normals

using a low pass kernel. The ﬁlters in (Pereira and

Velho, 2009) have the advantage that they guarantee

that the resulting normals correspond to a surface.

To assist the user in deﬁning the editing region, we

use a segmentation method (Felzenszwalb and Hut-

tenlocher, 2004) which was extended (Toler-Franklin

et al., 2007) to handle RGBN images. The procedure

is fast and is well suited to interactive applications. It

also takes into account the normal and color channels,

using all available information to improve results. It

is also possible to segment objects based solely on

geometry. To avoid over-segmenting, a bilateral ﬁlter

should be used prior to segmentation to remove noise

while preserving edges.

For replicating the RGBN sample on a base

RGBN, we extended jump map-based texture syn-

thesis (Zelinka and Garland, 2004), more speciﬁ-

cally jump maps on RGBN images (Zelinka et al.,

2005). This method is non-parametric and pixel-

based, avoiding the need of a local parametrizations

on normal maps. It does not produce the best qual-

ity results but it is the only interactive time technique,

allowing for easy user experimentation. This strategy

also handles base geometry distortions by varying im-

age edge lengths during synthesis as a function of the

normals.

During texture synthesis, colors are deﬁned for

each pixel. However the synthesized normals (high

frequency) still have to be combined with the ﬁltered

input normals (low frequencies). We want to com-

bine normals controlling which frequency bands we

are replacing or editing. We follow the approach of

(Pereira and Velho, 2009), where two combination

schemes were proposed: the linear model and the ro-

tation model. The linear model combines normals by

looking at them as gradients. This strategy is sim-

pler and has the advantage that the resulting normals

are guaranteed to correspond to a real surface, but the

equivalent position displacements are restricted to the

z-direction. On the other hand, the rotation model de-

forms the details to follow the base shape before com-

bining. We use this method for all examples.

4 JUMPMAPS ON RGBNS

We begin this section by reviewing jump map-based

texture synthesis on a regular image. We also describe

a few principles that makes the method better suited to

our application. We then discuss (Zelinka et al., 2005)

the extension to color synthesis on RGBN images.

The simple example-based synthesis algorithms

(Efros and Leung, 1999; Efros and Freeman, 2001)

exhaustively search the input for a best match. This

search is done for each pixel or patch being synthe-

sized. In (Zelinka and Garland, 2004), Zelinka splits

texture synthesis in two phases: analysis and syn-

thesis. Note that in previous methods analysis was

Figure 3: Jump Map synthesis results.

NORMAL SYNTHESIS ON RGBN IMAGES

Figure 4: The highlighted neighborhoods are similar, but a

jump between them introduces offsets, breaking brick align-

ment. A bigger mask size (19x19) improves results.

being done online and would use an already synthe-

sized neighborhood as a query. Zelinka’s insight is

that while this neighborhood is only known at synthe-

sis time it will resemble an existing one in the tex-

ture example. As such, we can precalculate and store

the similarities between all neighborhoods in the ex-

amplar. The Jump Map data structure holds for each

examplar pixel a list of jumps to similar pixels.

During synthesis, the output texture is traversed

and pixels are sequentially copied from the example.

Eventually the input texture border will be reached,

that is when the jump map comes in hand. As the

border approaches, a jump is randomly selected from

the Jump Map. As such, there is an inﬁnite amount of

texture to be copied.

The analysis phase is cast as a nearest-neighbor

(NN) problem in a neighborhood space. Each pixel’s

square neighborhood is encoded in an M

feature vec-

tor, using the L

norm for comparisons. Notice that

two parameters inﬂuence performance M and N (in-

put sample size). Since analysis with small values of

M won’t represent the texture appropriately we are

easily led to a high dimensional NN problem which

would be too slow to handle directly. Instead, the au-

thors use an approximate nearest neighbors (ANN)

data structure (Mount, 1998) that allows very fast

queries. For further optimization, PCA is used for

dimensionality reduction of the feature vector.

As Zelinka notices, jump map synthesis works

best for stochastic textures and weak structured tex-

tures. While quality results can be obtained with

highly structured textures (Figure 10), these are ex-

ceptions. The reason can be seen in Figure 4. We

see very similar neighborhoods, but if a jump is taken

between them offsets will be introduced in the synthe-

sized bricks. This problem happened because a small

neighborhood was used for analysis. While increas-

ing M improves results, it also increases analysis time.

For highly structured textures it is more important

to match structure than to transfer details. We use

multiresolution to ignore sample details during analy-

Figure 5: In both images, analysis was done with a 100x100

sample, but the second was synthesized with a 500x500

higher resolution sample, which would be hard to analyze.

sis. We notice that it is possible to use different values

of N (different resolutions) for analysis and synthesis,

virtually allowing larger masks. We use small sam-

ples for fast analysis, while we use detailed samples

for quality synthesis (Figure 5). Zelinka uses mul-

tiresolution but only to improve PCA compression.

To extend this algorithms to RGBN images, two

problems have to be solved: synthesizing normals

and synthesizing on normal images. The next sec-

tion presents our solution to the ﬁrst problem. To

handle the second one (Zelinka et al., 2005) adapted

jump map-based color synthesis to normal images.

On RGBN images, we need to vary the scale of the

synthesis spatially due to foreshortening (Figure 6-

a). A unit pixel offset in the output image induces

a displacement in the represented surface, which in

turns induces an offset in texture space. These param-

eters may be global or may vary smoothly over the

surface (Zhang et al., 2003). By approximating the

surface locally by a plane orthogonal to the normal

n, we can obtain the displacement d

in texture space

as a function of the displacement d

in output image

space and of the projection p of d

onto the surface

|p|

, p = d

− < n, d

> n.

(a) (b)

Figure 6: a) Due to foreshortening, texture scale varies spa-

tially according to the normals. b) The leaves were repli-

cated generating a normal map. We show here a shaded

version of the synthesized map.

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

5 NORMAL TEXTURES

We have extended the analysis and synthesis steps

of the jump maps method to synthesize normals. In

the analysis phase, we take a normal map sample

representing our desired texture and we are asked

to build a jump map for it. Since the basic prim-

itive in jump map analysis is comparing neighbor-

hoods, we must settle on which metric to use. In

the color setting, the sum of the euclidean metric for

each pixel neighborhood was used. However normals

are in the unit-sphere S

and as a consequence each

neighborhood feature vector is in the cartesian prod-

uct S

× S

× ... × S

. Therefore, the sum of the pixel

normal metrics will induce a natural deﬁnition of a

neighborhood metric, we only have to choose a nor-

mal metric. We analyze three different metrics: eu-

clidean, geodesic and dot product based.

The geodesic distance obtained from the angle

cos

−1

(< n

, n

>) is a natural choice (intrinsic dis-

tance) and it would be easy to adapt the O(N

) so-

lution to the NN problem in the analysis phase. On

the other hand, since cos

−1

is a non-linear function, it

is very hard to adapt either PCA or ANN, the funda-

mental algorithms that allow building jump maps in

reasonable time. Linearity could be obtained by us-

ing a dot product based distance 1− < n

, n

>, but

it falls far from the geodesic distance (Figure 7) spe-

cially for small values. In NN problems, these are the

exactly the ones we are most interested in. This leads

us to our last metric alternative: Euclidean. The Eu-

clidean metric is a very good approximation for the

geodesic metric for small distances since their deriva-

tives at zero agree. Therefore, the Euclidean distance

gives us a good compromise between simplicity and

precision, so this is our choice for texture analysis.

As for synthesis, the order in which pixels of the

output image are synthesized is important to reduce

directionality bias. This happens because each pixel

is synthesized based on only one of its neighbors.

Zelinka found that following Hilbert curves produces

much better results than scan-line or serpentine traver-

Figure 7: Different normal distances as function of the an-

gle between the normals.

Figure 8: The detail normals n

deﬁned in R are combined

with the image normals.

sals. However, we do not use Hilbert traversal. The

reason is we look for synthesis in subsets of RGBN

images, which could be deﬁned by either user or au-

tomated segmentation. Since these regions may have

very complex shapes and topologies, it would be com-

plicated to use a synthesis order based on Hilbert

curves. Instead, we used a depth-ﬁrst search (DFS)

using a 4-connected pixel neighborhood. We recur-

sively visit each pixels and its neighbors. The naive

DFS algorithm produces unpleasant results with a di-

rectionality bias. This is a consequence of always

visiting a ﬁxed neighbor ﬁrst, for example the north

neighbor. A simple alternative is to use DFS, proceed-

ing to each cardinal direction in random order. This

breaks directionality and generates results almost as

good as Hilbert traversal ones, as demonstrated by all

results in this manuscript. The DFS traversal has two

advantages. First, it only processes the pixels being

synthesized. Second, it can respect discontinuities in

the normals. For instance, in Figure 6-a we would

not want synthesis to cross from the upper part of the

shell to the lower part, we would like them to be in

different connected components in the graph. This is

easy to handle, if two neighboring pixels have differ-

ent normals (deﬁned by a threshold), they are simply

not connected in the graph.

6 INTEGRABILITY ANALYSIS

In this section, we discuss the conditions for the re-

sulting normals to be integrable, that is, for it to cor-

respond to a surface. For simplicity, we only analyze

the linear combination method (Section 3) and disre-

gard the foresight distortions introduced by scaling.

Given a base normal ﬁeld n

deﬁned in the entire

image I (Figure 8) and a synthesized detail normal

ﬁeld n

deﬁned in R ⊂ I, the problem of combining

normals is generating a new normal ﬁeld which agrees

with n

everywhere, but is inﬂuenced in R by n

. We

refer to their respective height functions as b and h.

We can look at a normal image n as a 2D vector

ﬁeld w (Section 3). If this ﬁeld is the gradient of

a height function, we say it is a conservative vector

ﬁeld. This means our normal image does correspond

NORMAL SYNTHESIS ON RGBN IMAGES

to a surface.

The authors of (Pereira and Velho, 2009) show

that conservative results can be guaranteed when

combining normals by adding their vector ﬁelds coun-

terparts w

and w

. Three conditions must be satis-

ﬁed. First of all, they require w

and w

to be con-

servative. Second, since h is only deﬁned in R, we

must extend it as zero outside the edited region. This

requires w

to fall smoothly to zero close to ∂R and

be equal to 0 outside. However this is not enough the

added detail must not introduce level changes outside

R or it will create discontinuities in height.

Figure 9: When the low frequencies of the exemplar are

not removed, it is harder to infer pattern. This generates an

uneven result.

What restrictions do we have to make to guarantee

that normal synthesis satisﬁes the three requirements

above? To begin with, w

might not fall smoothly or

not even fall to zero in ∂R, which would result in dis-

continuities in w. In many applications (Figure 10),

is already discontinuous in ∂R so that new discon-

tinuities are not created. Second, synthesis will not

introduce level changes if w

only contains high fre-

quency content which tends to oscillate and cancel it-

self. Hence, the restriction on w

is enforced with

the high-pass ﬁlter on the exemplars. In addition, tex-

ture synthesis methods in general, and jump maps in

particular, do not introduce repetitions and so no low

frequencies are created.

It seems very unlikely that non-parametric tex-

ture synthesis methods can guarantee the generation

of conservative ﬁelds in arbitrary domains, since only

local operations are performed. On the other hand,

local operations seem enough to generate curl-free

ﬁelds that guarantee that w is conservative under the

additional hypothesis that R is simply connected (does

not contain holes). Traditional techniques aim at gen-

erating texture such that each pixel’s neighborhood

closely resembles a neighborhood in the exemplar.

We argue that the curl is also similar in this neighbor-

hood. This means given curl-free exemplars, the syn-

thesis will generate approximately curl-free textures.

As Figure 10 shows, quality results can be obtained

even when R is not simply connected.

7 RESULTS

In this section, we will discuss some of the results ob-

tained. Shaded images were produced with one light

source. In some examples, uniform albedo is used

to better highlight shape. In Figure 12-b, only the

normals of the shell were changed, colors were unaf-

fected. The base geometry was combined with high

frequency normals extracted from rust. These new

normals retain the original shape of the shell but give

the appearance of a new material. It is true that with

some trial and error rust could be generated with a

procedural noise. On the other hand, structures syn-

thesis from real objects on the shell (Figure 12-c, 13)

can only be accomplished with texture from example

methods. These structured examples show how syn-

thesized details follow the base geometry.

In Figure 6-b, we can see a normal map sampled

from scanned leaves and synthesized normals. Uni-

form albedo was used for shading. There are some

aliasing artifacts which could be handled by synthe-

sizing in a higher resolution and down-sampling. This

is possible, since synthesis time scales linearly.

The original model contained a wooden board

with real vegetables (see Figure 10, upper left). Seg-

mentation was able to separate the objects. We added

the relief and color of the armor of a stone Chinese

warrior to the board. The complex topology of this

object was not a problem and DFS was able to guide

synthesis around it. Rust was synthesized on the veg-

etables (normal and color). The ﬁne scale normals on

the normal map are hard to spot on the shaded version.

In Figure 9, a sample of the normals of a pine

cone was used for synthesis. Low frequencies were

not removed. This can be seen as the exemplar varies

smoothly from light (top) to dark blue (bottom). It

has two consequences, ﬁrst it is harder for the analy-

sis phase to infer pattern. Second the ﬁnal result is un-

even. The shaded image shows some darker regions

which are not facing the light.

As in Textureshop (Fang and Hart, 2004), shape

from shading can be used to recover normals from

photographs. We have also used it to obtain the tex-

ture exemplar (Figure 11). A swatch was extracted

from the lizard’s arm (b) and combined with smooth

hand normals (d). The ﬁnal image (e) was shaded

under diffuse lighting, ignoring the lizard’s skin re-

ﬂectance properties. For more realistic results, a syn-

thesis method that can handle morphing between tex-

tures is required. Notice how the texture of the ﬁn-

gers, the hand and the arm of the lizard are differ-

ent. Very high frequency detail like human hand lines

could be recombined in the ﬁnal result.

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

Figure 10: A shaded image of edited vegetables. Automatic segmentation followed by texture synthesis is a powerful tool for

material replacement. The vegetables were turned into rust metal.

8 CONCLUSIONS

We have developed a method to synthesize normal

textures on RGBNs. Our pipeline includes normal ﬁl-

tering to control which frequency bands we edit or

replace. We discuss conditions on the exemplars and

models that guarantee that the resulting normal image

is a realizable surface.

Requiring the deformations to extend to 0 out-

side R is a limitation of our method, blending tech-

niques should be investigated in the future to en-

force this property on any synthesized deformation.

A limitation of jump map-based synthesis is that be-

ing pixel-based, it has problems with very structured

textures. On the other hand, it is harder to adapt

less local methods to RGBN images, since the met-

ric of bigger neighborhoods is non-trivial. In future

work, we would like to use normal synthesis in the

context of inpainting normals to ﬁll missing regions.

Another direction is to use a projective atlas (Velho

and Sossai Jr., 2007) to extend this work to a surface.

This new synthesis would take into account not only

macrostructure (mesh) but also mesostructure in the

form of existing normal maps.

(a) Texture source (b) Normal map

(e) Shaded image (f) Synthesized normals

Figure 11: Shape from shading was used to estimate nor-

mals (b,d). A small sample of the lizard’s arm was ﬁltered

and synthesized over the hand (e). Lighting (e) was set sim-

ilar to the original. Only the normals were used to produce

the ﬁnal result.

NORMAL SYNTHESIS ON RGBN IMAGES

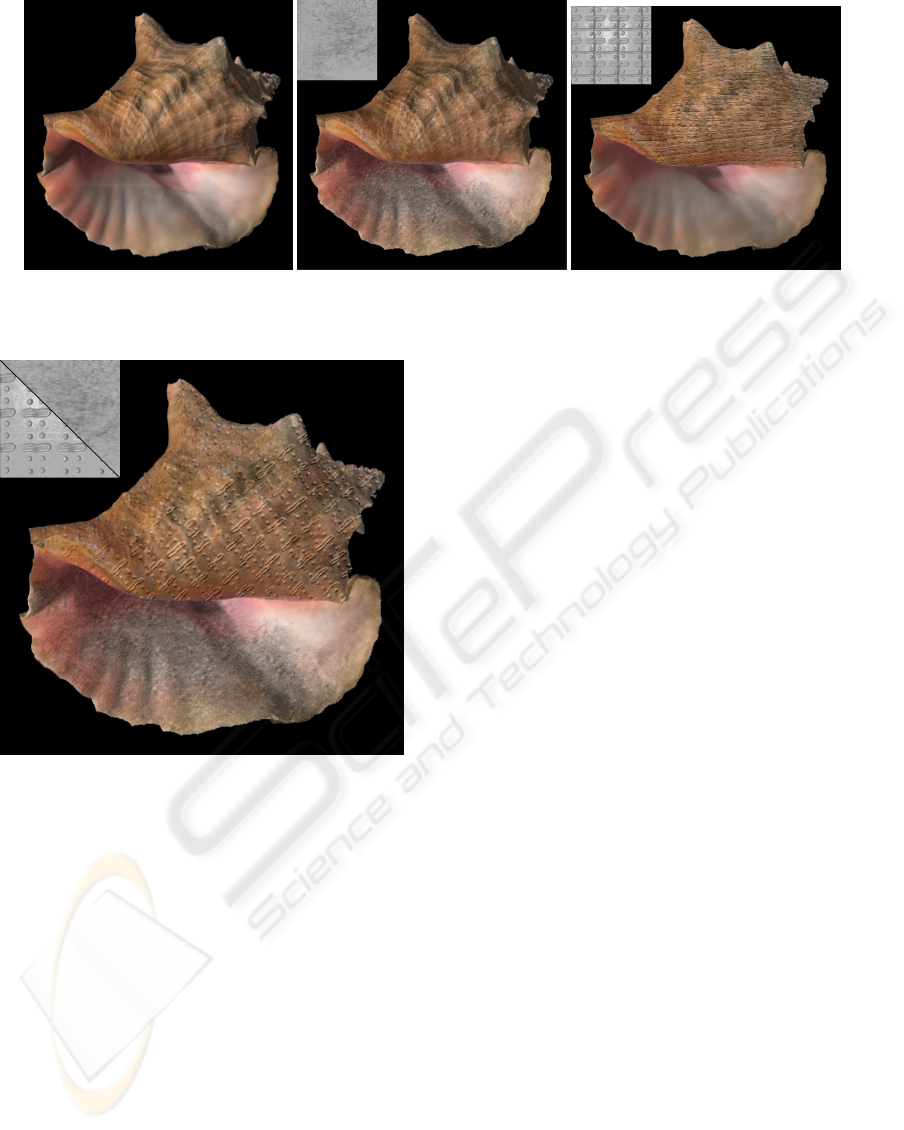
(a) Original Shell (b) Rust Normals (c) Armor Normals

Figure 12: The small images show the exemplars used under a direct light source. Images are embedded in high resolution.

Figure 13: Structured texture synthesis.

REFERENCES

Bernardini, F., Rushmeier, H., Martin, I. M., Mittleman,

J., and Taubin, G. (2002). Building a digital model

of michelangelo’s ﬂorentine pieta. IEEE Computer

Graphics and Applications.

Chen, T., Goesele, M., and Seidel, H.-P. (2006). Mesostruc-

ture from specularity. In IEEE CVPR ’06.

Cignoni, P., Montani, C., Scopigno, R., and Rocchini, C.

(1998). A general method for preserving attribute val-

ues on simpliﬁed meshes. In VIS ’98: Proceedings of

the conference on Visualization ’98. IEEE Computer

Society Press.

Cohen, J., Olano, M., and Manocha, D. (1998).

Appearance-preserving simpliﬁcation. In SIGGRAPH

’98. ACM.

Efros, A. and Leung, T. (1999). Texture synthesis by non-

parametric sampling. In ICCV ’99. IEEE Computer

Society.

Efros, A. A. and Freeman, W. T. (2001). Image quilting

for texture synthesis and transfer. In SIGGRAPH ’01.

ACM.

Fang, H. and Hart, J. C. (2004). Textureshop: texture syn-

thesis as a photograph editing tool. In SIGGRAPH

’04. ACM.

Felzenszwalb, P. F. and Huttenlocher, D. P. (2004). Efﬁcient

graph-based image segmentation. Int. J. Comput. Vi-

sion, 59(2):167–181.

Haro, A., Essa, I. A., and Guenter, B. K. (2001). Real-

time photo-realistic physically based rendering of ﬁne

scale human skin structure. Proceedings of the 12th

Eurographics Workshop on Rendering Techniques.

Kautz, J., Heidrich, W., and Seidel, H.-P. (2001). Real-time

bump map synthesis. HWWS ’01: EUROGRAPHICS

workshop on Graphics hardware.

Mount, D. M. (1998). Ann programming manual. Technical

report.

Pereira, T. and Velho, L. (2009). Rgbn image editing. Pro-

ceedings of SIBGRAPI.

Toler-Franklin, C., Finkelstein, A., and Rusinkiewicz, S.

(2007). Illustration of complex real-world objects us-

ing images with normals. In NPAR.

Turk, G. (2001). Texture synthesis on surfaces. In SIG-

GRAPH ’01. ACM.

Velho, L. and Sossai Jr., J. (2007). Projective texture at-

las construction for 3d photography. Vis. Comput.,

23(9):621–629.

Wei, L.-Y. and Levoy, M. (2001). Texture synthesis over

arbitrary manifold surfaces. In SIGGRAPH ’01. ACM.

Woodham, R. J. (1989). Photometric method for determin-

ing surface orientation from multiple images. pages

513–531.

Zelinka, S., Fang, H., Garland, M., and Hart, J. C. (2005).

Interactive material replacement in photographs. In

GI ’05: Proceedings of Graphics Interface 2005.

Zelinka, S. and Garland, M. (2004). Jump map-based

interactive texture synthesis. ACM Trans. Graph.,

23(4):930–962.

Zhang, J., Zhou, K., Velho, L., Guo, B., and Shum, H.-Y.

(2003). Synthesis of progressively-variant textures on

arbitrary surfaces. In SIGGRAPH ’03. ACM.

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications