UTOMATIC CONSTRUCTION OF HIERARCHICAL HIDDEN

MARKOV MODEL STRUCTURE FOR DISCOVERING SEMANTIC

PATTERNS IN MOTION DATA

O. Samko, A. D. Marshall and P. L. Rosin

School of Computer Science, Cardiff University, Cardiff, U.K.

Keywords:

HHMM structure, Pattern recognition, Motion analysis.

Abstract:

The objective of this paper is to automatically build a Hierarchical Hidden Markov Model (HHMM) (Fine

et al., 1998) structure to detect semantic patterns from data with an unknown structure by exploring the natural

hierarchical decomposition embedded in the data. The problem is important for effective motion data repre-

sentation and analysis in a variety of applications: ﬁlm and game making, military, entertainment, sport and

medicine. We propose to represent the patterns of the data as an HHMM built utilising a two-stage learning al-

gorithm. The novelty of our method is that it is the ﬁrst fully automated approach to build an HHMM structure

for motion data. Experimental results on different motion features (3D and angular pose coordinates, silhou-

ettes extracted from the video sequence) demonstrate the approach is effective at automatically constructing

efﬁcient HHMM with a structure which naturally represents the underlying motion that allows for accurate

modelling of the data for applications such as tracking and motion resynthesis.

1 INTRODUCTION

Hierarchical Hidden Markov Models (HHMMs)

(Fine et al., 1998) have become popular for modelling

real world data which have non-linear variations and

underlying hierarchical structure. This form of mod-

elling has been found useful in applications such as

handwritten character recognition (Fine et al., 1998),

activity recognition (Kawanaka et al., 2006), (Nguyen

and Venkatesh, 2008) and DNA sequence analysis

(Choi et al., 2009), (Hu et al., 2000).

The automatic discovery of an HHMM topol-

ogy from original data is an important yet compli-

cated problem. This has not to date gained that

much attention; some work in this area has been re-

ported in (Xie et al., 2003), (Youngblood and Cook,

2007). The structure discovery algorithm by Xie (Xie

et al., 2003) employs the Markov Chain Monte Carlo

(MCMC) method to determine structure parameters

for an HHMM in an unsupervised manner. This ap-

proach is used to discover patterns in video, namely

play and break, and is based on a bespoke proce-

dure to select features from the video. Youngblood

and Cook (Youngblood and Cook, 2007) examine the

problem of automatic learning of a human inhabitant

behavoural model. They extract sequential patterns

from inhabitant activities using the Episode Discov-

ery (ED) sequence mining algorithm. An HHMM is

created using low-level state information and high-

level sequential patterns. This is used to learn an ac-

tion policy for the environment. This model, as with

(Xie et al., 2003), was developed to represent speciﬁc

features inherent in the data.

We propose the algorithm, constructed with

the non-linear dimensionality reduction approach,

Isomap (Tenenbaum et al., 2000), and based on

Isomap’s ability to preserve data geometry at all

scales (Silva and Tenenbaum, 2003). Using this prop-

erty, we can explore the data trajectory in the em-

bedded space. We also employ the assumption of

the motion data trajectory smoothness during analy-

sis of the space. Under these conditions we propose

that by utilising hierarchical clustering we can con-

struct an HHMM topological structure in the Isomap

space, and the obtained HHMM is efﬁcient in explor-

ing semantic patterns in the motion data. We build

an HHMM using our algorithm and learn the model

with Dynamic Bayesian Network (DBN) (Murphy

and Paskin, 2001). After the model training, we test it

by exploring observed motion patterns from the new

unseen data.

275

Samko O., D. Marshall A. and L. Rosin P. (2010).

AUTOMATIC CONSTRUCTION OF HIERARCHICAL HIDDEN MARKOV MODEL STRUCTURE FOR DISCOVERING SEMANTIC PATTERNS IN

MOTION DATA.

In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 275-280

DOI: 10.5220/0002815202750280

 SciTePress

We investigate the ﬁrst stage of data process-

ing, hierarchical content characterisation algorithm,

in Section 2. In Section 3, we automatically con-

struct a dynamic model for semantic pattern discov-

ery using parameters obtained at the ﬁrst stage. Sec-

tion 4 demonstrates the effectiveness of our algorithm

by applying it to the different motion data features,

namely silhouettes, 3D coordinates and angular (Ac-

claim) data. Conclusion and future work are given in

Section 5.

2 HIERARCHY CONSTRUCTION

The algorithm’s ﬁrst stage consists of three main

steps, described below in separate subsections. The

algorithm is generic, in that it is able to work with

various unlabelled feature sequences, extracted from

the original motion data. Also we assume that the data

is complete, i.e. without missing (unobserved) values.

2.1 Trajectory Extraction

Isomap, as a manifold learning technique, represents

global data relationships in a low dimensional space,

maximally preserving geodesic distances between all

pairs of data points (Tenenbaum et al., 2000). We em-

ploy this Isomap ability and represent an input data as

a point-wise trajectory in an embedded space for the

initial data analysis.

The basic idea of the Isomap algorithm is to use

geodesic distances on a neighborhood graph in the

framework of the Multidimensional scaling (MDS)

algorithm. The success of Isomap in the data repre-

sentation and model accuracy depends on being able

to choose an appropriate neighborhood size. We use

the method for automatic selection of this parameter

described in (Samko et al., 2006).

2.2 GMM on the Embedded Space

The Gaussian Mixture Model (GMM) is a ﬂexible

and powerful method for unsupervised data grouping

(McLachlan and Basford, 1988). In addition to group-

ing, it gives us parameters which we use to initialise

our dynamic model at the second stage of the data

processing.

To choose the number of Gaussian clusters we use

the method described in (Bowden, 2000). Accord-

ing to this method, the Characteristic Cost Graph is

produced and the optimal number of clusters is deter-

mined by locating a point where increasing the num-

ber of clusters does not lead to a signiﬁcant decrease

in the resulting cost. We perform a more accurate es-

timation of that point with the procedure for threshold

estimation (Rosin, 2001).

Figure 1 shows an example of Gaussian clustering

in the Isomap space. The data points form a trajectory

which represents the original data sequence.

−4000

−2000

2000

4000

−2000

−1000

1000

−1000

−500

500

1000

Figure 1: GMM clustering (10 clusters) of the walking data

in Isomap space.

2.3 Hierarchical Data Organisation

To construct a hierarchy over the obtained clusters,

we employ the standard agglomerative clustering al-

gorithm (Duda et al., 2000) because this approach at-

tempts to place the input elements in a hierarchy in

which the distance within the tree reﬂects similarity

between the elements. As an input, we use means

of the Gaussian clusters. The result of the hierarchi-

cal clustering is represented as a dendrogram tree, see

Figure 3 for example.

3 DYNAMIC PATTERNS

DISCOVERY

Using the hierarchy constructed in the previous sec-

tion as a basis, we now aim to construct a two-level

HHMM which considers parts of motion as separate

submodels. The top HHMM level corresponds to the

main actions in the motion data, and at the bottom the

initial data sequence is divided into subsequences ac-

cording to the actions they represent. The choice of

the number of levels is natural: every data sequence

has at least a single pattern (subsequence), while hav-

ing more levels could be unnecessary for many appli-

cations as well as being computationally expensive.

3.1 HHMM Deﬁnition

An HHMM forms a hierarchy of HMMs, where a top

level HMM can have sub HMMs as its hidden nodes.

Figure 2 shows an example of the HHMM state transi-

tion diagram, which consists of two HMMs with three

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

276

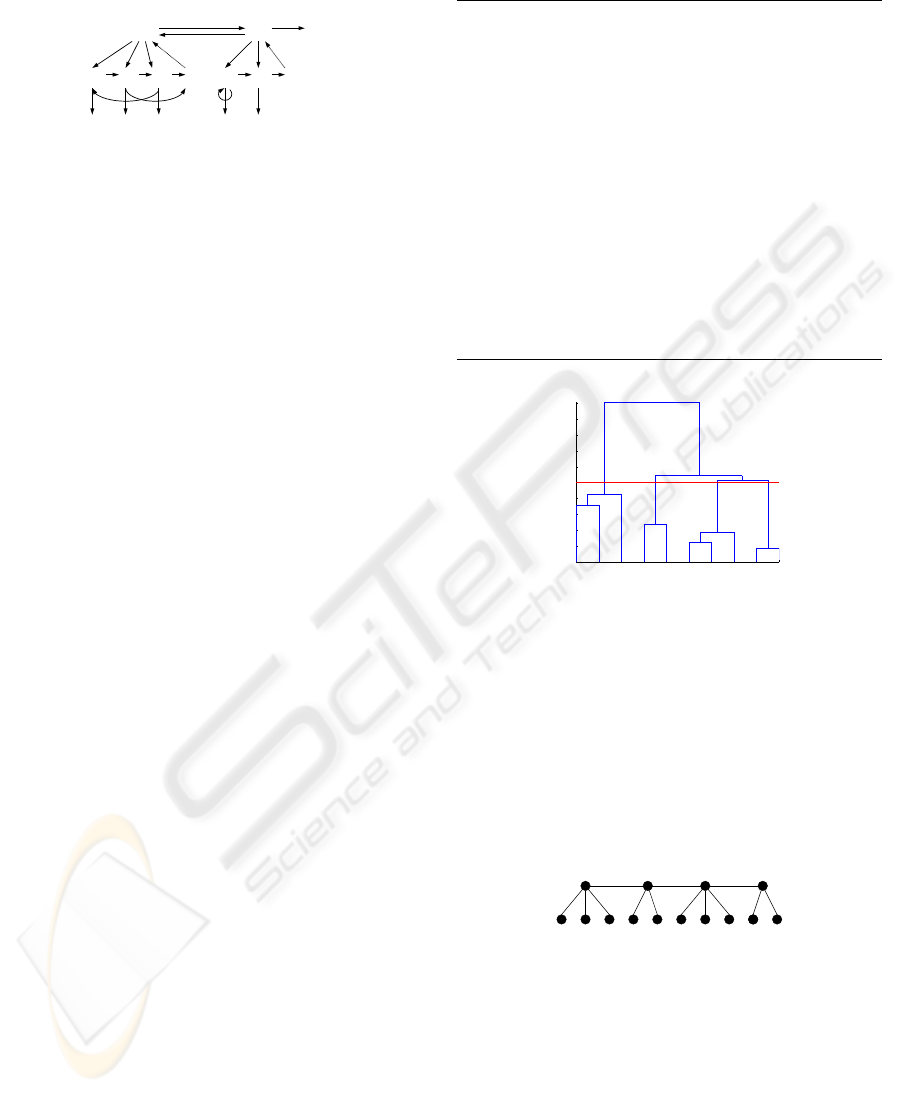
and two states at the bottom level, and one two-state

HMM at the top level.

Q Q Q Q Q

Figure 2: A two-level HHMM with observations at the bot-

tom. Black edges denote vertical and horizontal transitions

between states and observations O. Dashed edges denote re-

turns from the end state of each level e to the level’s parent

state Q

(t is the state index, d is the hierarchy level).

A full HHMM is deﬁned as a 3-tuple

H =< λ, ζ, Σ > (1)

Here λ is a set of parameters, ζ is the topological

structure of the model, and Σ is an observation alpha-

bet. The set of parameters λ consists of a horizontal

transition matrix A, mapping the transition probability

between child nodes of the same parent; an observa-

tion probability distribution B and a vertical transition

vector Π that assigns the transition probability from a

hidden node to its child nodes:

λ =< A, B, Π > (2)

The topology ζ speciﬁes the number of levels, the

state space at each level, and the parent-children re-

lationship between levels. The states include “pro-

duction states” that emit observations and “abstract

states” which are hidden states. The observation al-

phabet Σ consists of all possible observation ﬁnite

strings.

3.2 HHMM Structure Construction

In an HHMM, every higher-level state corresponds to

a stream produced by lower-level sub-states, a transi-

tion at the top level is invoked only when the lower-

level HMM enters an exit state. Therefore it is natural

to construct an HHMM in a “bottom-up” manner.

After the hierarchical clustering algorithm is ap-

plied to the initial data, we get the data dendrogram

representation as in Figure 3. We use this represen-

tation to construct the HHMM structure. The pro-

posed HHMM structure construction algorithm out-

line is presented in Table 1.

We apply a heuristic approach for construction of

the HHMM structure: we cut the dendrogram using

the mean distance between clusters measure, and use

the clustering speciﬁed by the dendrogram at that cut-

off level. The purpose of this is to provide clusters

that are similar enough to be grouped together, and

Table 1: An automatic HHMM structure construction algo-

rithm.

1. Find the dendrogram cut-off level using the mean

distance between clusters. Remove all dendro-

gram levels above the cut-off and intermediate

levels between this level and the bottom dendro-

gram level. Label nodes.

2. Set the top-HMM number of states and number

of bottom-HMMs equal to the number of clusters

at the cut-off level. Set the number of bottom-

HMMs states equal to the number of clusters in

the corresponding dendrogram branches.

3. Identify transitions between the states using

GMM labels. Set a transition between the states

and Q

if there exist successive points from

the data sequence y

, y

t+1

such that y

∈ Q

and

t+1

∈ Q

500

1000

1500

2000

2500

3000

3500

4000

4500

5000

Data index

Distance

Dendrogram

1 8 9 2 10 3 7

5 4 6

Figure 3: A dendrogram for the walking data. The red line

indicates the cut-off level. Four clusters at the top level are

formed in this example.

the sizes of these groups are large enough to construct

a regular HMM with them. Figure 4 illustrates the hi-

erarchy for the motion data, obtained from the den-

drogram shown in Figure 3. Using this representation

we set the number of states for each HMM (for this

particular example these numbers are 4 for the top-

HMM, and 3, 2, 3 and 2 for the bottom level HMMs).

1 8 9 2 10 3 7 5 4 6

11 12 13 14

Figure 4: A hierarchical representation for the motion data.

Figure 5 shows the resulting HHMM structure (ζ

from Equation 1) - state transition diagram. Black

arrows denote state transitions, and dotted arrows de-

note returns to the parents states. Our HHMM does

not have a fully connected topology because we lim-

ited the transitions by using the GMM labels obtained

at the ﬁrst stage. This reduces the number of transi-

tion matrix non-zero elements and simpliﬁes calcula-

tion of the HHMM parameters.

AUTOMATIC CONSTRUCTION OF HIERARCHICAL HIDDEN MARKOV MODEL STRUCTURE FOR

DISCOVERING SEMANTIC PATTERNS IN MOTION DATA

277

5 3 7 2 10 6 4 9 1 8

13 12 14 11

Figure 5: An HHMM state transition diagram for the mo-

tion data.

3.3 Learning HHMM Parameters

To determine the HHMM fully, we need to set λ from

Equation 2. We convert an HHMM into a DBN, to

reduce the time complexity of computation, and learn

the DBN parameters instead to ﬁnd the parameters of

Equation 2. We use standard DBN parameter learn-

ing procedures, which are best described in (Murphy

and Paskin, 2001). To initialise the model, we use the

GMM parameters from the previous section.

4 EXPERIMENTS

Now we evaluate how the proposed algorithm pro-

cesses different types of motion data, represented by

3D coordinates, angular coordinates and silhouettes

extracted from the video sequences. The data we use

contains a wide range of variation both in upper and

lower body parts, and sequences from several hun-

dreds to several thousands of frames. In Section 4.1,

we extract semantic patterns and evaluate the model

for a gymnastic exercise sequence from the CMU mo-

tion capture (MoCap) database

, where motion fea-

tures are represented by 3D angular coordinates. In

Section 4.2 we address the model’s classiﬁcation abil-

ity with 3D coordinates of a walking person. And

ﬁnally, the model is constructed with silhouette se-

quences from the IXMAS motion database

4.1 CMU MoCap Data

The algorithm input data here is represented by 32

angular coordinates (the video preprocessing and fea-

ture extraction details can be found on the CMU web-

site). This motion data sequence consists of 5357

frames, and contains 8 exercises: jumps, jog, squats,

side twists, lateral bending, side stretch, forward-

backward stretch and forward stretch. In this example

we demonstrate that our method is able to work with

a variety of movements, as well as with long data se-

quences.

We reduce the dimensionality of the original space

to 3 using the automatic method (Samko et al., 2006),

http://mocap.cs.cmu.edu

http://perception.inrialpes.fr

and perform clustering. In our experiments we as-

sume that motion data has smooth transformations

between points in the embedded space and there-

fore clusters include chains of the neighbour elements

from the original data sequence, i.e. data subse-

quences. Also note that in the Isomap space similar

clusters are close to each other; we use this property

in our model construction.

Figure 6 shows a schematic representation of the

HHMM structure obtained by our algorithm. Each

hidden state here is illustrated by the mean pose for

that state. This Figure shows that we are able to ex-

tract the above mentioned main patterns from the un-

labelled data. There are six states at the top HMM,

which represent jumps, jog, squats, side twists, lat-

eral bending and stretches. At the bottom level we get

six HMMs whose number of states range from two

(squats HMM: down and up states) to seven (lateral

bending). The stretches sub-HMM consists of ﬁve

states and represents three exercises at once: side,

forward-backward and forward stretches.

To test the model we take another fragment of

swordplay motion, which consists of 2300 frames and

includes jumps, jog, squats and side twists exercises.

We project the test data into Isomap space using the

kernel function given in (Bengio et al., 2004) and clas-

sify it with our model.

The pattern with the maximum probability is used

to label the data. To verify the result and make a com-

parison with other methods, we manually label train

data with these patterns. We consider this labelling

as a ground truth, and perform classiﬁcation evalu-

ation with our semi-supervised model, unsupervised

HHMM and ﬂat HMM over the test data. We use the

same structure for the unsupervised HHMM obtained

from our hierarchical algorithm, but without param-

eters initialisation from the algorithm ﬁrst stage, and

the HMM consisted of the bottom level states of our

model. The classiﬁcation results are shown in the ﬁrst

column of Table 2. Using our semi-supervised algo-

rithm, we get better accuracy than the other methods.

An example of state of the art results, (Junejo et al.,

2008) recently reported the average recognition ac-

curacy 91.98% for the pre-deﬁned actions from the

CMU MoCap database. The achieved accuracy shows

the potential advantage of our method in automatic

action recognition.

4.2 Walking Data

We use the sequence of 218 frames which represents

motion of a walking person, consisting of two steps,

right turn and another step. The initial feature param-

eters represent the coordinates of human (arms, legs,

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

278

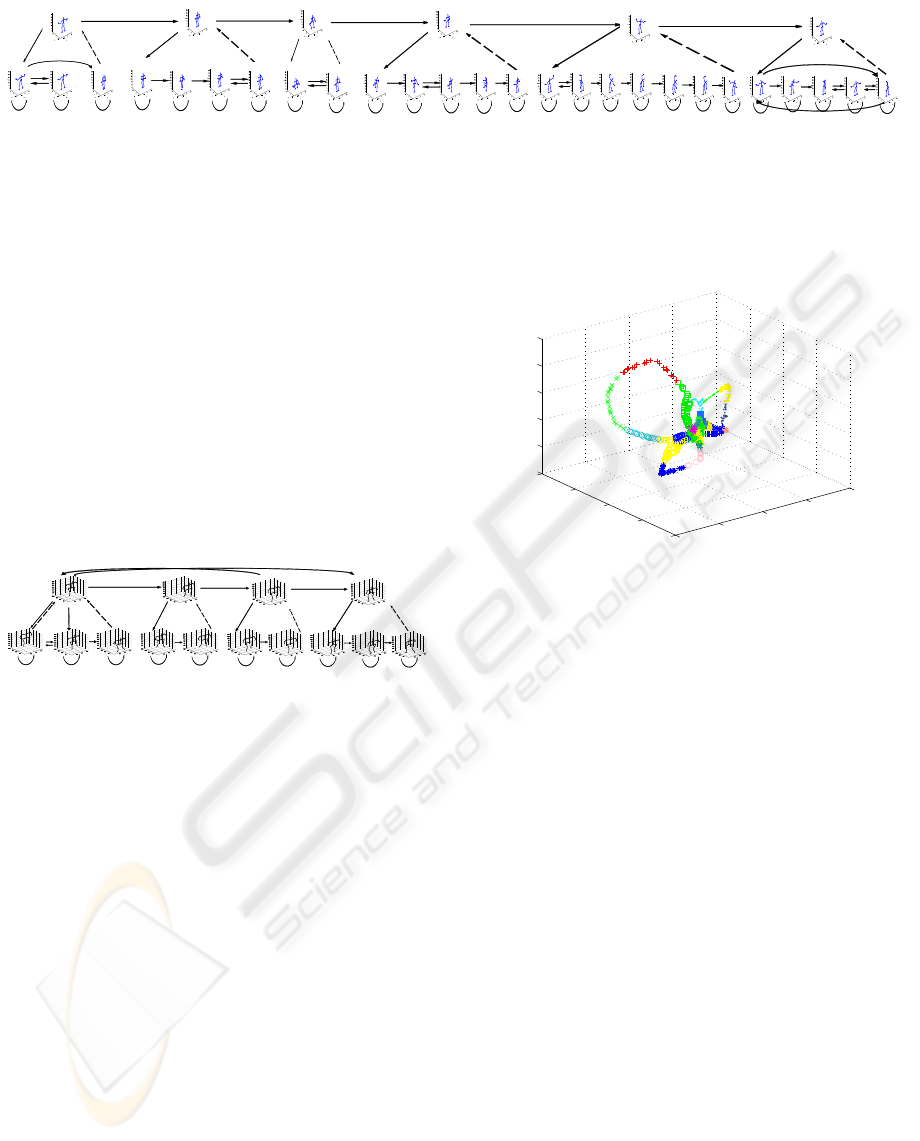
Figure 6: An HHMM state transition diagram for the exercise data.

torso) in the 3D space. Each pose is characterised by

17 points on the body.

We showed some intermediate results for this ex-

ample to illustrate the algorithm in Figures 1, 3, 4.

The HHMM structure is presented in Figure 5 and

Figure 7. We get one top level HMM, which includes

four sub-HMMs. “5-3-7”-states HMM correspond to

the pattern which represents the motion beginning and

start of the turn. “2-10” HMM corresponds to the

sequence pattern with left leg moving down and the

right leg lifting up motions. “6-4”-state HMM move-

ment is opposite to the previous pattern: the right leg

moving down and the left leg lifting up. Finally, “9-

1-8” HMM represents the turn and step after turn pat-

tern. Thus the automatically constructed HHMM ex-

tracts “natural” units from the original data.

Figure 7: An HHMM state transition diagram for the walk-

ing data.

The results of classiﬁcation are shown in the sec-

ond column of Table 2. We can say that our semi-

supervised HHMM is able to correctly identify the se-

mantic patterns in the test data and classify the motion

patterns better than other methods.

4.3 IXMAS Data

The INRIA Xmas Motion Acquisition (IXMAS) se-

quence we used here contains 11 actions: check

watch, cross arms, scratch head, yoga, turn around,

walk, wave, punch, kick, point and throw away. The

silhouettes were extracted from the video using a stan-

dard background subtraction technique, modelling

each pixel as a Gaussian in RGB space.

Although raw silhouette pixels are not the opti-

mal feature for motion analysis, we use it to show the

algorithm’s ability to work with such difﬁcult input

data. For the Isomap algorithm, it is much harder to

extract main motion features from silhouettes, to em-

bed them into the low dimensional space, and to pro-

duce useful trajectories for further analysis. Isomap

space for the silhouette data is more knotted than for

the coordinate data, which makes clustering and pat-

tern extraction more difﬁcult. Figure 8 illustrates the

embedded space for this example.

−0.4

−0.2

0.2

0.4

−0.4

−0.2

0.2

0.4

−0.2

−0.1

0.1

0.2

0.3

Figure 8: GMM clustering of the IXMAS data in embedded

space.

To test the algorithm we take the sequence of 1076

frames from the IXMAS database. It shows the front

view silhouettes of the person performing the above

actions in the above order.

Figure 9 shows the HHMM structure obtained by

our algorithm. In comparison to the coordinate data,

we get more transitions between the states (because

of the space knotting). As shown in this Figure, the

algorithm recognised ﬁve patterns in this data. The

ﬁrst pattern represents hand movements from a stand-

ing position and includes check watch, cross arms,

scratch head and wave actions. The second pattern

is the yoga action. The next recognised pattern is leg

movements and includes turn around, walk and kick

actions. The fourth pattern is hand movements with

legs apart, this contains punch and point actions. And

the last pattern is the throw away action.

We use another sequence of similar length to test

the model. The classiﬁcation results are shown in

the last column of Table 2. The accuracy is lower

compared with our earlier experiments because of the

increased complexity of its trajectory in the Isomap

space, but it can be seen that our algorithm is able

to ﬁnd the meaningful patterns even from such data.

Also it is comparable to the result reported by (Junejo

et al., 2008) for the pre-deﬁned actions from this data

AUTOMATIC CONSTRUCTION OF HIERARCHICAL HIDDEN MARKOV MODEL STRUCTURE FOR

DISCOVERING SEMANTIC PATTERNS IN MOTION DATA

279

Figure 9: An HHMM state transition diagram for the IXMAS data.

Table 2: Classiﬁcation results (rate of correct classiﬁcation).

Method Exercise Walk IXMAS

Semi-sup. HHMM 93.57% 96.95% 71.63%

Unsuperv. HHMM 91.13% 93.13% 65.43%

Flat HMM 90.65% 92.37% 65.43%

set (72.5%), taking into account that we do not make

any manual settings.

5 CONCLUSIONS

We have presented a novel method for the automatic

discovery of an HHMM topological structure applied

to ﬁnding semantic patterns in an unlabelled motion

sequence. We demonstrated our algorithm’s ability

to work with various data features obtained from dif-

ferent types of mocap/video sources. Since the al-

gorithm is not linked with any a priori information

from the data, it could be used with various data types

(for example, in DNA sequence analysis). Our algo-

rithm is fully automated with no additional conﬁgura-

tion parameters required.

In order to develop a more detailed knowledge of

the strengths and robustness of our algorithm, a more

thorough experimental evaluation of our system will

be carried out in future work. We hope to improve the

robustness and compactness of our model by using al-

ternative clustering algorithms, and we plan to involve

probability estimation to the cut-off level detection.

REFERENCES

Bengio, Y., Paiement, J., and Vincent, P. (2004). Out-

of-sample extensions for LLE, Isomap, MDS, Eigen-

maps and spectral clustering. Advances in Neural In-

formation Processing Systems 16.

Bowden, R. (2000). Learning non-linear models of shape

and motion. PhD Thesis, Dept Systems Engineering,

Brunel University.

Choi, H., Nesvizhskii, A., Ghosh, D., and Qin, Z. (2009).

Hierarchical HMM with application to joint analy-

sis of ChIP-seq and ChIP-chip data. Bioinformatics,

(25):1715–1721.

Duda, R. O., Hart, P. E., and Stork, D. G. (2000). Pattern

classiﬁcation. Wiley-Interscience Publication.

Fine, S., Singer, Y., and Tishby, N. (1998). The Hierarchi-

cal Hidden Markov Model: Analysis and applications.

Machine Learning, 32(1):41–62.

Hu, M., Ingram, C., Sirski, M., Pal, C., Swamy, S., and Pat-

ten, C. (2000). A hierarchical HMM implementation

for vertebrate gene splice site prediction. Technical

report, Dept. of Computer Science, University of Wa-

terloo.

Junejo, I., Dexter, E., Laptev, I., and Perez, P. (2008).

Cross-view action recognition from temporal self-

similarities. ECCV, pages 293–306.

Kawanaka, D., Okatani, T., and Deguchi, K. (2006).

HHMM based recognition of human activity. IEICE

Transactions Inf. and Syst., 89(7):2180–2185.

McLachlan, G. and Basford, K. (1988). Mixture mod-

els: Inference and applications to clustering. Marcel

Dekker.

Murphy, K. and Paskin, M. (2001). Linear time inference in

Hierarchical HMMs. Proc. Neural Information Pro-

cessing Systems.

Nguyen, N. and Venkatesh, S. (2008). Discovery of activ-

ity structures using the Hierarchical Hidden Markov

Model. BMVC, pages 112–122.

Rosin, P. L. (2001). Unimodal thresholding. Pattern Recog-

nition, 34:2083–2096.

Samko, O., Marshall, A., and Rosin, P. (2006). Selection of

the optimal parameter value for the isomap algorithm.

Pattern Rocognition Letters, 27:968–979.

Silva, V. and Tenenbaum, J. (2003). Local versus global

methods for nonlinear dimensionality reduction. In

Advances in Neural Information Processing Systems,

volume 15.

Tenenbaum, J., Silva, V., and Langford, J. (2000). A global

geometric framework for nonlinear dimensionality re-

duction. Science, 290:2319–2323.

Xie, L., Chang, S., Divakaran, A., and Sun, H. (2003).

Feature selection and order identiﬁcation for unsu-

pervised discovery of statistical temporal structures in

video. IEEE International Conference on Image Pro-

cessing (ICIP), 1:29–32.

Youngblood, G. M. and Cook, D. J. (2007). Data mining

for hierarchical model creation. IEEE Transactions

on Systems, Man, and Cybernetics, Part C, 37(4):561–

572.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

280