
TREE-STRUCTURED TEMPORAL INFORMATION FOR FAST
HISTOGRAM COMPUTATION
S
´
everine Dubuisson
Laboratoire d’Informatique de Paris 6 (LIP6/UPMC), 104 avenue du Pr
´
esident Kennedy, 75016, Paris, France
Keywords:
Fast histogram computation, Integral histogram.
Abstract:
In this paper we present a new method for fast histogram computing. Based on the known tree-representation
histogram of a region, also called reference histogram,, we want to compute the one of another region. The
idea consists in computing the spatial differences between these two regions and encode it to update the
histogram. We never need to store complete histograms, except the reference image one (as a preprocessing
step). We compare our approach with the well-known integral histogram, and obtain better results in terms of
processing time while reducing the memory footprint. We show theoretically and with experimental results
the superiority of our approach in many cases. Finally, we demonstrate the advantage of this method on a
visual tracking application using a particle filter by improving its time computing.
1 INTRODUCTION
Histograms are often used in image processing for
feature representation (colors, edges, etc.). The com-
plex nature of images implies a large amount of infor-
mation to be stored in histograms, requiring more and
more computation time. Many approaches in com-
puter vision require multiple retrievals of histograms
for rectangular patches of an input image. Each one
is developed for a specific application, such as for im-
age retrieval (Halawani and Burkhardt, 2005), con-
trast enhancing (Caselles et al., 1999) or object recog-
nition (Gevers, 2001). In such approaches, we dispose
a reference histogram and try to find the region of the
current image whose histogram is the most similar.
The similarity is given by a measure that has to be
computed between each target histogram and the ref-
erence one. This implies the computation of a lot of
target histograms, that can be very time consuming,
and may also need a lot of storage. The main goal
is then to reduce the computation time, while using
small data structures, requiring less memory.
In this article, we propose a new histogram com-
putation by using a data structure only coding the
pixel differences between two frames of a video se-
quence. This data structure is updated over time on
pixel changes information and is used to define the
histogram of the whole new image or a part of it.
We never need to store the complete histogram and
our representation is compact because it only contains
variation information between two frames. The main
advantages of our approach are that it is not dependent
on the histogram quantization (i.e. number of bins),
it is fast to compute (comparing to other approaches)
and compact. Section 2 reviews some of the previ-
ous works on fast histogram computation. Section 3
presents our method compared with the well-known
integral histogram. Section 4 gives some theoreti-
cal considerations about time computation and size
of storage needed. In Section 5, some experimental
results show the benefit of our approach. In Section 6
we illustrate the capability of our method on a real ap-
plication: object tracking using particle filtering. Fi-
nally, we give concluding remarks in Section 7.
2 PREVIOUS WORKS
An histogram is computed into a region by brows-
ing all the pixels of this region. If lots of histograms
have to be computed locally around a set of salient
points, it can be advantageous to use the histogram
of a nearby region and to update it to obtain the his-
togram of the current region, instead of computing all
the histograms. This can be applied in cases of spa-
tial filtering, but also in temporal filtering in video se-
quences, when trying to find displacements of objects
between frames. A lot of works have been proposed
to reduce the histogram computing time.
13
Dubuisson S. (2010).
TREE-STRUCTURED TEMPORAL INFORMATION FOR FAST HISTOGRAM COMPUTATION.
In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 13-22
DOI: 10.5220/0002815800130022
Copyright
c
SciTePress
One of the first work on redundancy computation re-
duction was proposed by (Tang et al., 1979), in the
context of image filtering. Considering the histogram
H
R
of a region R, the histogram of a region Q is com-
puted by keeping the histogram of their intersection
region, removing the pixels of R that do not belong
to Q, and adding those from Q that do not belong to
R. This approach is efficient only in cases of large
intersection between regions. Recently this method
has been improved by (Perreault and Hebert, 2007) in
the context of median filtering. In (Sizintsev et al.,
2008) the authors present the distributive histogram.
They use the property for disjoint regions R and Q
that H(R
S
Q) = H(R) + H(Q). Their approach can
then easily be adapted to non-rectangular regions that
is not the case of previous approaches.
A fast way to compute histograms in terms of
time computation is the integral histogram (Porikli,
2005) (IH), inspired from integral images (Viola and
Jones, 2001), that is now used in many applica-
tions needing massive histogram computations by lo-
calized searches, especially in recent tracking algo-
rithms (Adam et al., 2006; Wang et al., 2007). This
approach is inspired from integral image and consists
in computing the histogram of any region of an im-
age using only four operations (two additions and two
subtractions). IH is a cumulative function whose cells
IH(r, c) contain the histogram of an image area con-
taining its r first rows and c first columns. Then:
IH(r, c) = I(r, c) + IH(r − 1, c)
+ IH(r, c − 1) − IH(r − 1, c − 1)
Once the integral histogram has been computed
over all cells, we can derive any histogram of a
sub-region only using four elementary operations,
see (Porikli, 2005) for more details. For example, the
histogram of a w × h region R with pixel (r,c) as bot-
tom right corner is given by:
H
R
= IH(r, c) − IH(r − h, c)
− IH(r, c −w) + IH(r − h, c − w)
The main drawback of integral histogram is the large
amount of data needed to be stored. For an N × M
image, the size of the array IH needed is N × M × B,
where B is the number of bins in the histogram. We
can find a good comparative study of some of these
previous exposed method in (Sizintsev et al., 2008).
However, our approach is totally different than previ-
ous ones: we never need to encode histograms (except
the reference one), but only the temporal differences
between two images, and use them to determine new
histograms. The size of the data structure, and the his-
togram computation time only depends on the varia-
tions between frames.
3 PROPOSED APPROACH:
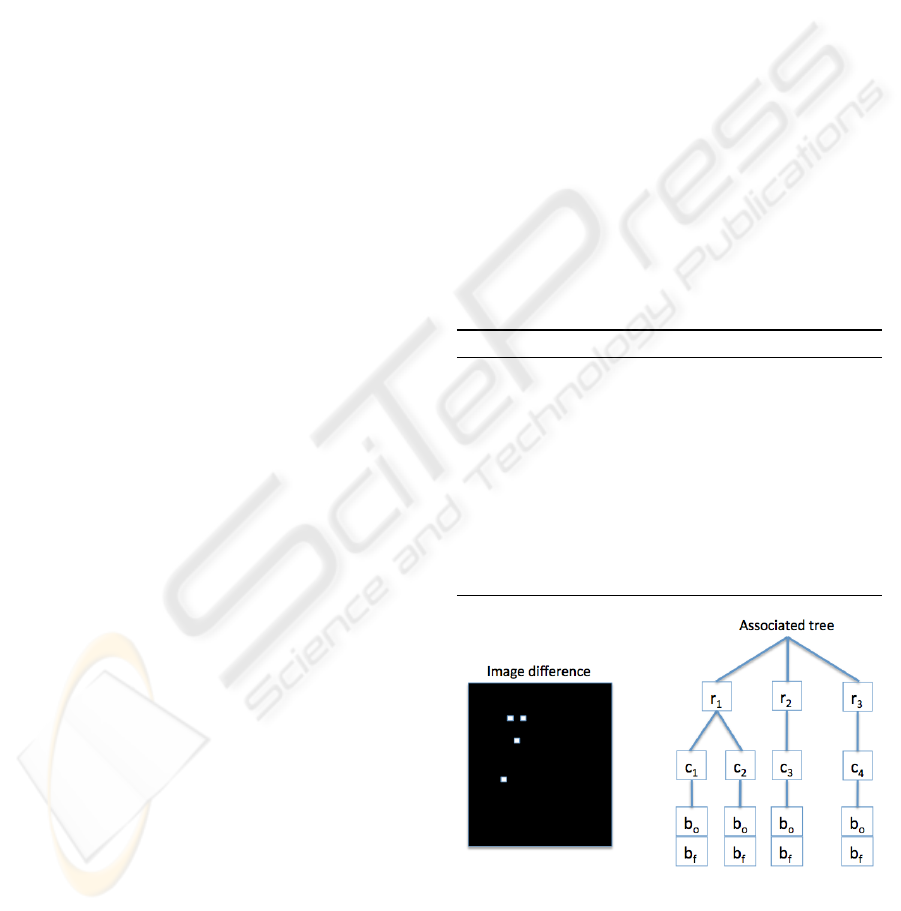
TEMPORAL HISTOGRAM
Assume that we have a reference histogram H (from
the reference image I
1
), and want to compute his-
tograms in a new image I
2
only using H and temporal
variations between I
1
and I
2
. Temporal variations are
obtained with the image difference and encoded by a
tree data structure with height h
T
= 3. Nodes at the
level h = 1 correspond to the rows r
i
of the image I
2
where there is a difference with I
1
, and nodes at the
level h = 2 correspond to the columns numbers c
j
.
Leaf nodes contain, for each pixel (r
i
, c
j
), the differ-
ence between I
1
and I
2
, the initial bin it was belonging
to in H, and the bin it will belong to in the histogram
of the updated histogram. Figure 1 shows a basic ex-
ample of the construction of this data structure. On
the left, the image difference between I
1
and I
2
shows
only four different pixels, situated in three different
rows r
1
, r
2
and r
3
, and four different columns c
1
, c
2
,
c
3
and c
4
. For each pixel (r, c), we also have to store
its original and new bins, respectively b
o
and b
f
. Al-
gorithm 1 summarizes this process.
Algorithm 1. Temporal data structure construction.
T ← {}
Compute the image difference D = I
1
− I
2
for all D(r, c) 6= 0 do
b
o
← bin of I
1
(r, c); b
f
← bin of I
2
(r, c)
if node r does not exist in T then
Create branch r − c − (b
o
b
f
) in T
else
Add branch c − (b
o
b
f
) to node r in T
end if
end for
Figure 1: Construction of the data structure associated with
the image reference I
d
, on the left. For each non-zero value
pixel of I
d
, we store its new row number r
i
, column number
c
j
and original and final bins, respectively b
o
and b
f
.
Once we have the reference histogram H
R
and the dif-
ference tree T , we can derive any histogram of a re-
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
14

gion R in I
2
, as described in Algorithm 2. We then
just need to browse the data structure to determine if
some pixels have changed in this region between the
two images. For each changed pixel, we have to mod-
ify H
R
by removing one from the bin b
o
and adding
one to the bin b
f
. This is a very simple but efficient
way to compute histograms because we just perform
the necessary operations (where change has been de-
tected). In the next Section, we give some theoretical
comparative results between our approach and inte-
gral histogram.
Algorithm 2. Histogram computation of a region R.
Extract the sub-tree T
R
from T , containing chang-
ing pixels in R between the two frames
for all node branch r − c − b
o
− b
f
in T
R
do
H
R
(b
o
) ← H
R
(b
o
) − 1
H
R
(b
f
) ← H
R
(b
f
) + 1
end for
4 THEORETICAL STUDY:
MEMORY AND
COMPUTATION COST
IH is, in our opinion, the best in the sense that it re-
quires low computation time and is flexible enough
to adapt to many applications therefore it is the one
we have chosen for comparison with our approach.
In this section, we the compare our approach with IH
in terms of number of operations necessary to com-
pute histograms, and size of storage needed for the
data structures. We are considering an image I of size
N × M, and B is the number of bins in the histograms.
The histogram of the reference image has to be com-
puted as a preliminary step for both approaches: we
then do not consider this common step. We also do
not consider the allocation operations for the two data
structures (an array for IH and a tree for TH), but this
is clear that the tree needs less allocation operations
than an array, for a fixed number of pixels, because
it only stores 4 values per changing pixel, whereas IH
stores a whole histogram per pixel. The determination
of the bin of a current pixel requires one division and
one floor: we call f
b
this operation, and a an addition
(or a subtraction). Both methods require two steps:
1. the data structure construction, then
2. the data access for the computation a a new his-
togram.
We first consider and compare independently both
steps.
4.1 Construction of Data Structures
For IH, we need to browse all pixels I(r,c) of the im-
age, determine its bin value, and compute the integral
histogram using four operations a (see Section 2), for
each bin of the histogram. This part then needs a total
number of operations of:
(n
d
)
IH
= (4a + f
b
)NMB
This number of operations is a constant.
For TH, we first need to find non-zero values in the
image difference D (NMa operations). By scanning
D in the lexicographic order, we then create a branch
in the tree data structure for each non-zero value: let’s
be s the total number of non-zero value pixels (s ≤
(N × M)). For each of the s changing pixel, we have
to determine its new bin. The number of operations
needed for the construction of the tree is then:
(n
d
)
TH
= s f
b
+ NMa
Thus, to compare with IH, we have to consider two
special cases:
• In the best case, all the pixels in the image dif-
ference are zero-valued pixels: we need (n
d
)
TH
=
NMa operations to construct T.
• In the worst case, all the pixel values of the image
difference are different from zero, the construc-
tion of T can be done using a total number of op-
erations of:
(n
d
)
TH
= NM f
b
+ NMa = NM(a + f
b
)
Even in the worst case (all pixels have changed), the
number of operations necessary for the construction
of T is less than the one necessary for the integral
histogram construction. It should also be noticed that
(n
d
)
TH
does not depend on the number B of bins of
the histogram because we do not encode histogram
(and so do not need to browse all bins), only temporal
changes between images.
4.2 Histogram Computations
For both approaches, we consider the problem of
computing the histogram H
R
of any region R = [R
h
×
R
w
] of a new image I
2
knowing histograms in I
1
. For
both approaches, we consider the data access or ex-
traction as a negligible constant respectively c
IH
and
c
TH
(experimental results in Section 5 show that this
is a not a strong assumption).
For IH we just need two additions and two subtrac-
tions between values stored in the data structure, for
each bin of the histogram (see Section 2). Then, to
TREE-STRUCTURED TEMPORAL INFORMATION FOR FAST HISTOGRAM COMPUTATION
15

compute any histogram, we need a constant number
of operations:
(n
c
)
IH
= 4aB
This is a bit more complicated for TH. We first need
to extract the region R from T , if it does exist (we
have its histogram, see the introduction of this sec-
tion). Then, for each of the s
R
differences (s
R
≤ s if
R is a subregion of I, otherwise s
R
= s), we have to
remove one from the bin b
o
and add one to the bin b
f
.
The computation of a new histogram H
R
is done by a
total number of operations of:
(n
c
)
TH
= 2as
R
We consider the following special cases :
• In the best case, there is no difference between
the two considered regions: we need (n
c
)
TH
= 0
operation.
• In the worst case, all the pixel values have
changed between the two regions, we can com-
pute the histogram using a number of operations
of:
(n
c
)
TH
= 2a|R|
where |R| = R
h
× R
w
is the number of pixels in R.
If R = I
2
, then (n
c
)
TH
= 2aNM.
The efficiency of our approach for the new histogram
computation depends on the size of R and on the num-
ber of changing pixels between I
1
and I
2
. In the gen-
eral case, we have:
(n
c
)
TH
< (n
c
)
IH
if 2as
R
< 4aB ⇔ s
R
< 2B
We then conclude that TH is better as long as the num-
ber of changing pixels is less than twice the number
of bins on the histogram.
4.3 Total Computation
The total histogram computation time of a region in
the new image I
2
is fixed for IH:
(n
t
)
IH
= (4a + f
b
)NMB + 4aB
For TH, it depends on two major factors: (i) the
number s of changing pixels between I
1
and I
2
and
the number s
R
of changing pixels between (R)
I
1
and
(R)
I
2
. We need a total number of operation:
(n
t
)
TH
= s f
b
+ NMa + 2as
R
As previously, we can distinguish two cases:
• In he best case, there is no differences between the
considered regions and then T is empty, we need:
(n
t
)
TH
= NMa operations.
• In the worst case, all the pixel are different be-
tween I
1
and I
2
, so they are between (R)
I
1
and
(R)
I
2
), and we then need at total number of op-
erations:
(n
t
)
TH
= NM(a + f
b
) + 2a|R|
If R = I
2
, (n
t
)
TH
= NM(a + f
b
) + 2aNM =
NM(3a + f
b
).
We can compare the worst case with the fixed number
(n
t
)
IH
. IH depends on the size N × M of the image
and on the number B of bins of the histogram. TH
depends on the size of the image (conditioning the
potential number of changing pixels s) but also on the
region on which we compute the histogram. But the
data structure construction step requires less opera-
tions for TH (see Section 4.1). An histogram compu-
tation will require a number of operation depending
on the number of changing pixels between I
1
and I
2
(see Section 4.2)
4.4 Storage
We now compare the quantity of information neces-
sary for both approaches.
For IH, we need a constant-size array, containing a
total number of cells of:
(c)
IH
= NMB
We need one B-size array for each pixel (r, c),
corresponding to the histogram of the region from
rows 1 to N and columns 1 to M.
For TH we use a tree T as data structure whose size
depends on the number s of changing pixels between
images I
1
and I
2
. If we call n
r
the number of rows in
I
2
containing changing pixels, the number of nodes of
T is:
(c)
TH
= n
r
+ 3s
i.e. n
r
for the rows, and 3 nodes for each changing
pixel. We can distinguish two cases :
• In the best case, there is no difference between
regions, T is empty: (c)
TH
= 0.
• In the worst case, all the pixels are different, and
the size if the required data structure T is:
(c)
TH
= N + 3NM
Then, in the worst case (i.e. all the pixels have
changed between the two images or regions, that can
rarely happen):
(c)
IH
< (c)
TH
if NMB < N(1 + 3M) ⇔ B ≤ 3
In the most common case, (c)
IH
< (c)
TH
if NMB <
n
r
+ 3s. It is more than probable that the number of
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
16

changing pixels between the two images is less than
the total number of pixels. At most, if all these chang-
ing pixels are located on different rows (negative sce-
nario), we have n
r
+ 3s = s + 3s = 4s, so:
(c)
IH
< (c)
TH
if NMB < 4s ⇔ s >
NMB
4
Globally our histogram computation needs then less
storage.
The theoretical considerations about the number of
operations and storage needed for both approaches
developed in this section will next be verified with a
number of experimental results in the next Section.
5 EXPERIMENTAL RESULTS
In this section, we systematically compare integral
histogram (IH) with the proposed temporal histogram
(TH), since no method has been proved to be more
interesting than IH in terms of both computation time
and storage: it would not be relevant to perform com-
parisons with other methods based on this criteria.
In the next subsections, we call computation of a
histogram the two-steps process needed for both ap-
proaches: data structure construction and histogram
computation. All computation times reported in this
section correspond to the mean value over 100 differ-
ent tests.
5.1 Computation Time
In this section we propose to compare the computa-
tion times of integral and temporal histograms. In
Section 4, we have highlighted some parameters that
we directly involved, such as the number B of bins
of the histograms, the size N × M of the images, the
number s of changing pixels in the whole image, and
the number s
R
of changing pixels in the considered
region for histogram computation.
5.1.1 Video Sequences
Tests on different complete video sequences have
been performed. In this section we only present those
made on sequences “Walking” (15 frames of size
275 × 320), “Tennis” (89 frames of size 240 × 342)
and “Parking” (231 frames of size 576 × 768), see ex-
amples of frames in Figure 2. Some frames of these
sequences are shown in Figure 3. In these tests, we
are interested in the total computation time (along all
the sequence) needed for the computation of the his-
togram of randomly chosen regions of size 10 × 10
in each I
t
(t > 1) depending on the number of bins.
Figure 2: A frame from, from top to bottom: “Walking”,
“Tennis” and “Parking” sequences.
We can see in Figure 3 that the computation times ob-
tained with our approach are lower for each one of
these sequences. This is in part due to the fact that
the computation of the array of the integral histogram
takes a lot of time (and is performed at each frame),
even if the histogram time computation (just requiring
four operations) is small. This also shows that our ap-
proach is relatively stable with respect to the increas-
ing number of bins B, contrary to integral histogram,
whose computation time increases with B (drastically
for B = 256). This is due to the fact that, contrary to
the IH, the number B of bins does not affect a lot the
computation time (see Section 4.3) of TH is there are
only few changing between two frames. As there is
no ”best” number of bins, and different bin numbers
can reveal different features of the data: it is diffi-
cult to determine an optimal number of bins, without
making strong assumptions about the shape of the dis-
tributions. With our approach, it is not necessary to
make such assumptions.
5.1.2 Image and Size Variations
The performance of our approach principally depends
on the number s of changing pixels. The larger s, the
more consuming the method is. We then have tested
TREE-STRUCTURED TEMPORAL INFORMATION FOR FAST HISTOGRAM COMPUTATION
17

Figure 3: Tests on different video sequences (left column for an example of frame of, from top to bottom “Walking”, “Tennis”
and Parking” sequences). Bar diagram of an histogram computation time for both approaches, for different sequences and
increasing number of bins: “Walking” in blue, “Tennis” in green and “Parking” in orange (IH is represented as plain color,
TH as a transparency color).
the computation time as a function of s and compared
results with those obtained by the IH method.
In the first test, on the “Walking” video sequence,
I
1
is used as reference image and we evaluated the
histogram computation time for a region in the next
frame. Tests have been performed in frames I
1
, I
2
and
I
10
, in which respectively 0%, 25% and 40% of the
pixels vary from the first frame. Results are shown in
Figure 4, for different values of B. We can see that
the computation time of our approach increases as the
number of changing pixels increases, as highlighted
in Section 4 , but stay below the one obtained with
IH.
For the second test we have generated synthetic N ×N
images for different values of N and compared times
for the computation of the histogram with B = 16 bins
of this whole image (no pixel variation) for both ap-
proaches. Comparative results (in seconds) are re-
ported in Table 1. The increase of N does not influ-
ence a lot our approach, much while drastically de-
creasing IH performance. As no pixel have changed
between the two considered frames, the small time
computation increasing for TH is just due to the pixel
scanning of the new image that takes more time for a
large image than a smaller one: this explains why the
time computation for TH is equal to 0.0064 seconds
for N = 256 and to 0.4 for N = 2048.
Table 1: Time computation (in sec.) of an histogram with
B = 16 bins depending on the size of the image.
N 256 512 1024 2048
IH 0.8 3.23 12.9 52.1
TH 0.0064 0.02 0.09 0.4
The third test consists in considering a 1024 ×
1024 synthetic image and simulating a number s of
changing pixels, then computing the histogram with
B = 16 bins of this new image. We have compared
the computation times between both approaches: re-
sults are reported in Table 2. The computation time
with our approach stays below IH’s one until s = 10
6
.
This is not surprising, because our approach depends
on the number of changing pixels between images.
Anyway, s should has to have a large value before in-
creasing drastically our computation time.
Table 2: Time computation (in sec.) of a histogram with
B = 16 bins of a 1024 × 1024 synthetic image after having
s changed pixels.
s 10
2
10
3
10
4
10
5
10
6
% changing pixels 0.01 0.1 1 10 100
IH 12.9 13 12.9 13.1 12.9
TH 0.14 0.24 0.47 2.49 27.6
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
18
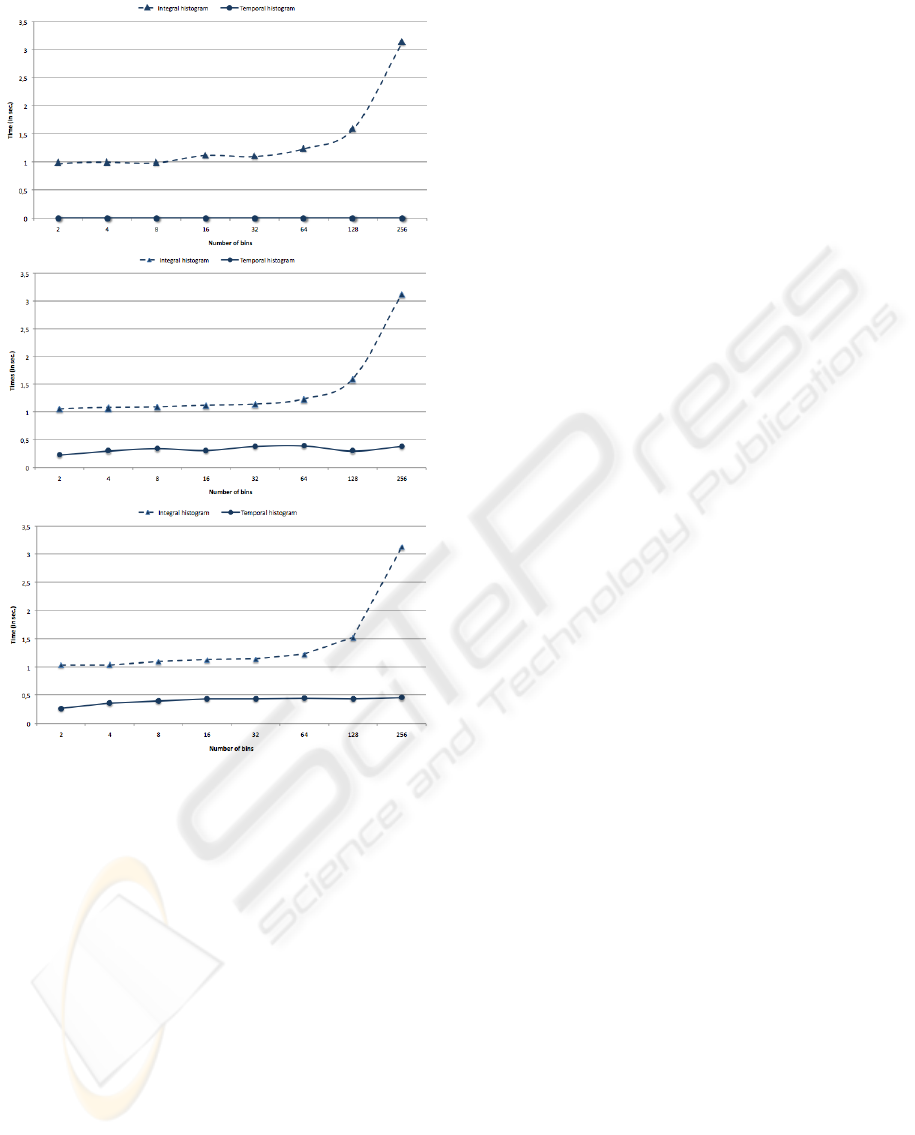
Figure 4: Comparison of integral histogram (IH) and tem-
poral histogram (TH) depending on the number of chang-
ing pixels between frames (“Walking” sequence, 275 × 320
frames). From top to bottom: 0% (between I
1
and I
1
), 25%
(between I
1
and I
2
) and 40% (between I
1
and I
10
) changing
pixels.
5.1.3 Number of Histogram Computations
The most time consuming part of IH is the construc-
tion of the array. However this array allows comput-
ing very quickly any histogram (or set of histograms)
using only four operations per histogram. In this sub-
section, we have launched a massive number of his-
togram computations and compared both approaches
in terms of computation time. The idea is to simu-
late the computation of target histograms in a search
window around a precise position, such as in spatial
filtering or temporal filtering (particle filtering for ex-
ample). Test have been made on the “Walking” se-
quence. We have chosen to present the results for dif-
ferent values of B. Results are shown in Figure 5.
Once again the performance depends on the quan-
tization of the histograms. For a strong quantiza-
tion (B = 2 or 4), IH and TH become equivalent for
1000 computations of histograms. For B = 8,16, 32,
methods are equivalent for 5000 computations. For
B = 128, 10000 computations are needed, and 25000
for B = 256. This interesting result shows that we
can keep good results (compared to IH) with no need
for a strong quantization of the histogram: TH does
not need to approximate histograms to provide good
computation times, which is a real advantage for his-
togram based search applications. We can however
see one limitation of the proposed approach when
dealing with too much histograms. In Section 4.2
we mentioned that TH is better then IH as long as
the number of changing pixels is less than twice the
number of bins on the histogram. It is clear that the
performances of TH then is depends on the number
of changing pixels between the two considerer re-
gions on which we compute histograms, and that is
the reason why our computation times increase with
the number of computed histograms considered. We
can notice than for a small histogram quantization, we
give very good results. Our TH is the suitable for
visual tracking applications where it is better not to
quantify histograms too much.
5.2 Storage
In this section we show that our approach does not
need to store a lot of information, contrary to integral
histogram. Table 3 reports the size (number of ele-
ments) required for the two data structures used for
the test shown in Figure 4, middle row (between two
consecutive frames of the sequence). The number of
elements necessary for IH increases with the num-
ber of bins, according to the results of Section 4.4,
in which we found (c)
IH
= NMB. For TH, it depends
on the number of changing pixels between the two
frames, (c)
TH
= n
r
+ 3s. A pixel is said to be chang-
ing between the two images if he changes its bins
in the histogram. This notion then strongly depends
on the histogram quantization: the more histogram is
quantified, the less a pixel changes its bins between
two images. That is the reason why the number of
elements of our data structure indirectly depends on
B. Note that the number of elements needed for IH
does not change if images are really different, which
is not the case for TH. We report in Table 4 the size
of these data structures depending on the number s
of changing pixels between two images generated as
random 1024 × 1024 matrices (same experiments as
in Section 5.1.2). We fix B = 16. For this case, the
number of elements necessary for integral histogram
TREE-STRUCTURED TEMPORAL INFORMATION FOR FAST HISTOGRAM COMPUTATION
19

Figure 5: Comparison of IH (dotted lines) and TH (plain lines) results for a massive number of histogram computations, for
different values of B, from top to bottom, from left to right, 2, 4, 8, 16, 32, 64, 128 and 256.
Table 3: Size (number of elements) of data structures re-
quired for both approaches, depending on B, the test corre-
sponds to the one of the middle row of Figure 4.
B IH TH
2 1.76 × 10
5
9.1 × 10
3
4 3.52 × 10
5
1.78 × 10
4
8 7.04 × 10
5
2.93 × 10
4
16 1.4 × 10
6
4.5 × 10
4
32 2.81 × 10
6
4.5 × 10
4
64 5.63 × 10
6
4.5 × 10
4
128 1.12 × 10
7
4.53 × 10
4
256 2.25 × 10
7
4.53 × 10
4
Table 4: Size (number of elements) of data structures re-
quired for both approaches, depending on the number s of
changing pixels between two images generated ss random
1024 × 1024 matrix, for B = 16. Percentage (%) of chang-
ing pixel are reported on the second line of this table.
s 10
2
10
3
10
4
10
5
10
6
% 0.01 0.1 1 10 100
IH 1.6 × 10
7
1.6 × 10
7
1.6 × 10
7
1.6 × 10
7
1.6 × 10
7
TH 1.3 × 10
3
3.8 × 10
3
2.9 × 10
4
2.8 × 10
5
2.8 × 10
6
is fixed such that (c)
IH
= NMB = 1024 × 1024×16 =
1.6 × 10
7
. Even considering 10
6
changing pixels (i.e.
100% of the initial image) in the region the histogram
is computed, the number of elements needed to store
it is always below the one IH needs.
To our opinion, TH is a good alternative to his-
togram computation in a lot of cases because it gives
a compact description of temporal change and good
computation time results for histogram computation.
Moreover, we never need to store histograms (except
for the reference image), that is a real advantage when
working on video sequences (for these cases, the ref-
erence image is the first of the sequence, and the his-
togram computation can be seen as a preprocessing
step).
6 INTEGRATION INTO
PARTICLE FILTER: FAST
PARTICLE WEIGHT
COMPUTATION
A good tracker should be able to predict in which
area of a new frame the object is. Among all the
methods, one can cite probabilistic trackers. In such
approaches, an object is characterized by a state se-
quence {x
k
}
k=1,...,n
whose evolution is specified by a
dynamic equation
x
k
= f
k
(x
k−1
, v
k
)
The goal of tracking is to estimate x
k
given a set of ob-
servations. The observations {y
k
}
k=1,...,m
, with m < n,
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
20

are related to the states by
y
k
= h
k
(x
k
, n
k
)
Usually, f
k
and h
k
are vector-valued, nonlinear and
time-varying transition functions, and v
k
and n
k
are
white Gaussian noise sequences, independent and
identically distributed. Tracking methods based on
particle filters (Gordon et al., 1993; Isard and Blake,
1998) can be applied under very weak hypotheses and
consist of two main steps:
1. a prediction of the object states in the scene (us-
ing previous information), that consists in propa-
gating particles according to a proposal function
(see (Chen, 2003)) ;
2. a correction of this prediction (using an available
observation of the scene), that consists in weight-
ing propagated particles according to a likelihood
function.
Joint Probability Data Association Filter
(JPDAF) (Vermaak et al., 2004) provides an op-
timal data solution in the Bayesian framework filter
and uses a weighted sum of all measurements near
the predicted state, each weight corresponding to the
posteriori probability for a measurement to come
from an object. Between two observations, the set of
particles evolves according to an underlying Markov
chain, following a specific transition function. Given
a new observation, each particle is assigned a weight
proportional to its likelihood of belonging to a tracked
object. New particles are randomly sampled to favor
particles with higher likelihood. A classical approach
consists in integrating the color distributions given by
histograms into particle filtering (P
´
erez et al., 2002),
by assigning a region (e.g. validation region) around
each particle and measuring the distance between the
distribution of pixels in this region and the one in the
area surrounding the object detected in a previous
frame. This context is ideal to test and compare our
approach in a specific framework.
For this test we measure the total computation
time of processing particle filtering in the first 60
frames of the “Rugby” sequence (240 × 320 frames,
see a frame in Figure 6): we are just interested on the
B = 16 bin histogram computation time around each
particle locations (that is the point of our paper). In
the first frame of the sequence, the validation region
(fixed size 30 × 40 pixels) containing the object to
track (one rugby player) is manually detected. JPADF
is then used along the sequence to automatically track
the object using N
p
particles. Then, the total computa-
tion times needed for each method is detailed below:
• For IH: one integral histogram H
i
in each frame
i = 1, . . . ,t of the sequence, then N
p
histogram
(one for each particle) computation using four op-
erations on H
i
.
• For TH: one integral histogram H (only in the first
frame), one tree T
i
construction in each frame i =
1, . . . ,t of the sequence, then, a histogram update
for each particle using H and T
i
.
Computation times are reported in Table 5 for differ-
ent values of N
p
. Computation times are lower with
our approach until N
p
= 5000 (tests have shown that
for N
p
= 8500, computation times are the same for
both methods). Note that, in practice, we do not need
so much particles in a classical problem. Our ap-
proach permits real-time particle filter based tracking
for a reasonable number of particles, which is a real
advantage. Note that the purpose of this test was not
to deal with tracking performances (that is the reason
why we do not give any results about quality results):
we just want to show that integrating TH into particle
filter correction step instead of IH can accelerate the
process. Moreover, we have shown than for similar
computation times, we can use more particles into the
frameworks integrating TH. As it is well-known (Gor-
don et al., 1993) that the particle filter converges with
a high number of particles N
p
, we can argue that in-
tegrating TI into a particle algorithm improves visual
tracking quality. Note that we have obtained same
kinds of results on different video sequences (people
tracking on “Parking” sequence and ball tracking on
“Tennis” sequence”)
Table 5: Total computation times (in sec.) for all histograms
(B=16) in the particle filter framework, depending on the
number N
p
of particles.
N
p
50 100 1000 5000 10000
IH 47.75 47.4 47.5 50.48 53.59
TH 23.5 23.6 28.31 40.4 76.24
7 CONCLUSIONS
We have presented in this paper a new method for fast
histogram computation, called temporal histogram
(TH). The principle consists in never encoding his-
tograms, but rather temporal changes between frames,
in order to update a first preprocessed histogram. This
technique presents two main advantages: we do not
need a large amount of information to store whole his-
tograms and it is less time consuming for histogram
computation. We have shown by theoretical and ex-
perimental results that our approach outperforms the
well-known integral histogram in terms of total com-
putation time and quantity of information to store.
Moreover, the introduction of TH into the particle fil-
tering framework has shown its usefulness for real-
TREE-STRUCTURED TEMPORAL INFORMATION FOR FAST HISTOGRAM COMPUTATION
21

Figure 6: Example frame of the “Rugby” sequence: red
rectangle is the validation region, green one the target re-
gion associated to one particle. Blue crosses symbolize
particle positions in frame around which we compute histi-
grams.
time applications in most common cases. Integral his-
togram requires the computation of the accumulator
array in each new image which takes a lot of time
(rarely taken into account in classical approaches).
TH computes histogram only if necessary (i.e. some
changes between images have been detected). Future
works will concern the generalization of this reason-
ing on different distance computation between his-
tograms, that requires to work directly on histogram
bins (Bhattacharyya (Bhattacharyya, 1943), L
1
norm,
euclidean distance etc.): the update would be done on
this distance, not on the histogram.
REFERENCES
Adam, A., Rivlin, E., and Shimshoni, I. (2006). Ro-
bust fragments-based tracking using the integral his-
togram. In Proc. IEEE Conf. on Computer Vision and
Pattern Recognition, pages 798–805.
Bhattacharyya, A. (1943). On a measure of divergence be-
tween two statistical populations defined by probabil-
ity distributions. Bulletin of the Calcutta Mathemati-
cal Society, 35:99–110.
Caselles, V., Lisani, J., Morel, J., and Sapiro, G. (1999).
Shape preserving local histogram modification. IEEE
Trans. on Image Processing, 8(2):220–230.
Chen, Z. (2003). Bayesian filtering: From kalman filters to
particle filters, and beyond. Technical report, McMas-
ter University.
Gevers, T. (2001). Robust histogram construction from
color invariants. IEEE Transactions on Pattern Anal-
ysis and Machine Intelligence, 26:113–118.
Gordon, N. J., Salmond, D. J., and Smith, A. F. M. (1993).
Novel approach to nonlinear/non-gaussian bayesian
state estimation. Radar and Signal Processing, IEE
Proceedings F, 140(2):107–113.
Halawani, A. and Burkhardt, H. (2005). On using his-
tograms of local invariant features for image retrieval.
In IAPR Conference on Machine Vision Applications,
pages 538–541.
Isard, M. and Blake, A. (1998). Condensation - conditional
density propagation for visual tracking. International
Journal of Computer Vision, 29:5–28.
P
´
erez, P., Hue, C., Vermaak, J., and Gangnet, M. (2002).
Color-based probabilistic tracking. In ECCV ’02:
Proceedings of the 7th European Conference on Com-
puter Vision-Part I, pages 661–675, London, UK.
Springer-Verlag.
Perreault, S. and Hebert, P. (2007). Median filtering in
constant time. IEEE Trans. on Image Processing,
16(9):2389–2394.
Porikli, F. (2005). Integral histogram: A fast way to extract
histograms in cartesian spaces. In Proc. IEEE Conf.
on Computer Vision and Pattern Recognition, pages
829–836.
Sizintsev, M., Derpanis, K. G., and Hogue, A. (2008).
Histogram-based search: A comparative study. in
Proc. IEEE Conf. on Computer Vision and Pattern
Recognition, pages 1–8.
Tang, G., Yang, G., and Huang, T. (1979). A fast two-
dimensional median filtering algorithm. In IEEE
Transactions on Acoustics, Speech and Signal Pro-
cessing, pages 13–18.
Vermaak, J., Godsill, S. J., and P
´
erez, P. (2004). Monte
carlo filtering for multi-target tracking and data asso-
ciation. IEEE Transactions on Aerospace and Elec-
tronic Systems, 41:309–332.
Viola, P. and Jones, M. (2001). Robust real-time object de-
tection. In International Journal of Computer Vision.
Wang, H., Suter, D., Schindler, K., and Shen, C. (2007).
Adaptive object tracking based on an effective appear-
ance filter. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 29(9):1661–1667.
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
22
